
本文是 Python 系列的 SciPy 补充篇。整套 Python 盘一盘系列目录如下:
在量化金融中,插值是个很常见的操作,即从一系列标准点对应的值”推出“非标准点的值,这个”推出“可以是内推 (interpolation),或称内插,也可以是外推 (extrapolation),或称外插。此外插值的维度可以是一维、二维甚至三维,在收益率曲线上插值用的是一维插值,在波动率平面上插值用的是二维插值。
收益率曲线插值:给定标准年限 t 和利率 r,如下图所示,对于非标准年限 ti 内插或者外插出 ri。

波动率平面插值:给定标准年限 t、标准行权价 K,和波动率 σ,如下图所示,对于非标准年限 ti 和非标准行权价 Kj,内插或者外插出 σij。
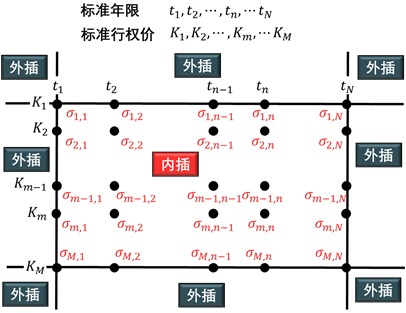
给定一组 (xi, yi),其中 i = 1, 2, ..., n,而且 xi 是有序的,称为「标准点」。插值就是对于任何新点 xnew,计算出对应的 ynew。换句话来说,插值就是在标准点之间建立分段函数 (piecewise function),把它们连起来。这样给定任意连续 x 值,带入函数就能计算出任意连续 y 值。
在 SciPy 中有个专门的函数 scipy.interpolate 是用来插值的,首先引进它并记为 spi。
import scipy.interpolate as spi
本贴分三章,第一章讲一维插值,第二章讲二维插值,第三章结合前两章的知识点对真实的 USD cap 估值。
用 scipy.interpolate 来插值函数 sin(x) + 0.5x。
x = np.linspace(-2 * np.pi, 2 * np.pi, 11)f = lambda x: np.sin(x) + 0.5 * xf(x)
array([-3.14159265, -1.56221761, -1.29717034, -1.84442231,
-1.57937505, 0. , 1.57937505, 1.84442231,
1.29717034, 1.56221761
, 3.14159265])
接下来介绍 scipy.interpolate 里面两大杀器:splrep 和 splev。两个函数名称都是以 spl 开头,全称 spline (样条),可以理解这两个函数都和样条有关。不同的是,两个函数名称以 rep 和 ev 结尾,它们的意思分别是:
splrep 和 splev 像是组合拳 (one two punch)
一图胜千言:

接下来仔细分析一下 tck。
tck = spi.splrep( x, f(x), k=1 )tck
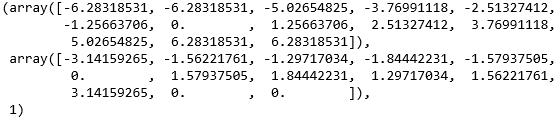
tck 就是样条对象,以元组形式返回,tck 这名字看起来很奇怪,实际指的是元组 (t, c, k) 里的三元素:
对照上图,tck 确实一个元组,包含两个 array 和一个标量 1,其中
第一个 array 是节点,即标准点,注意到一开始 x 只有 11 个,但现在是 13 个,首尾都往外补了一个和首尾一样的 x
第二个 array 是系数,注意它就是 y 在尾部补了两个 0
标量 1 是阶数,因为在调用 splrep 时就把 k 设成 1
可用 PPoly.from_spline 来查看每个分段函数的系数。
pp = spi.PPoly.from_spline(tck)pp.c.T
array([[ 1.25682673, -3.14159265],
[ 1.25682673, -3.14159265],
[ 0.21091791, -1.56221761],
[-0.43548928, -1.29717034],
[ 0.21091791, -1.84442231],
[ 1.25682673, -1.57937505],
[ 1.25682673, 0. ],
[ 0.21091791, 1.57937505],
[-0.43548928, 1.84442231],
[ 0.21091791, 1.29717034],
[ 1.25682673, 1.56221761],
[ 1.25682673, 3.14159265]])
tck 的系数数组里有 13 个元素,而上面数组大小是 (12, 2),12 表示 12 段,2 表示每段线性函数由 2 个系数确定。
把 x 和 tck 丢进 splev 函数,我们可以插出在 x 点对应的值 iy。
iy = spi.splev( x, tck )iy
array([-3.14159265, -1.56221761, -1.29717034, -1.84442231,
-1.57937505, 0. , 1.57937505, 1.84442231,
1.29717034, 1.56221761, 3.14159265])
用 Matplotlib 来可视化插值的 iy 和原函数 f(x) 发现 iy 都在 f(x) 上。Matplotlib 是之后的课题,现在读者可忽略其细节。

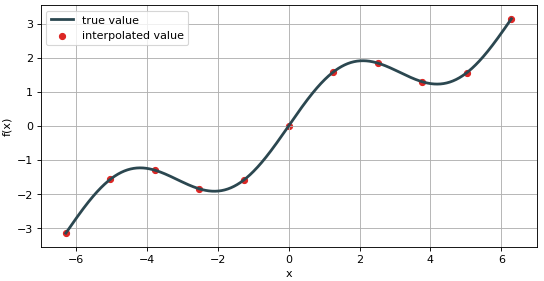
除了可视化,我们还可以用具体的数值结果来评估插值的效果:
np.allclose(f(x), iy)np.sum((f(x) - iy) ** 2) / len(x)
第一行 allclose 的结果都是 True 证明插值和原函数值完全吻合,第二行就是均方误差 (mean square error, MSE),0.0 也说明同样结果。
上面其实做的是在「标准点 x」上插值,那得到的结果当然等于「标准点 y」了。这种插值确实意义不大,但举这个例子只想让大家
明晰 splrep 和 splev 是怎么运作的
如何可视化插出来的值和原函数的值
如何用 allclose 来衡量插值和原函数值之间的差异
一旦弄明白了这些基础,接下来就可以秒懂更实际的例子了。
上面在「标准点 x」上插值有点作弊,现在我们在 50 个「非标准点 xd」上线性插值得到 iyd。
xd = np.linspace( 1.0, 3.0, 50 )iyd = spi.splev( xd, tck )print( xd, '\n\n', iyd )

密密麻麻的数字啥都看不出来,可视化一下把。

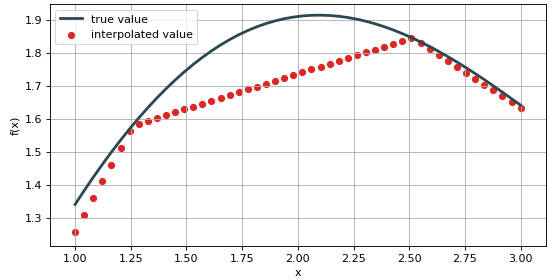
这插得是个什么鬼?红色插值点在第二段和深青色原函数差别也太远了吧 (MSE 也显示有差异)。
np.sum((f(xd) - iyd) ** 2) / len(xd)
问题出在哪儿呢?当「标准点 x」不密集时 (只有 11 个),分段线性函数来拟合 sin(x) + 0.5x 函数当然不会太好啦。那我们试试分段三次样条函数 (k = 3)。
tck = spi.splrep( x, f(x), k=3 )iyd = spi.splev( xd, tck )
可视化一下并计算 MSE 看看
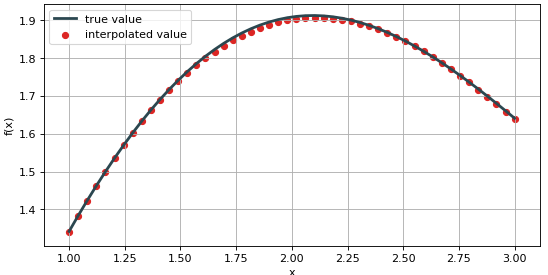
np.sum((f(xd) - iyd) ** 2) / len(xd)
视觉效果好多了!误差小多了!
有些时候新点 xnew 会越界,即不再原来 x 点的范围内,这时需要外插 (extrapolation) 而不是内插得到 ynew。在使用 splrep 和 splev 时,只需要在 splev() 函数中设定参数 ext:
三种外插方式的差异如下三图所示。
# 线性外插spi.splev(x_new, tck, ext=0)
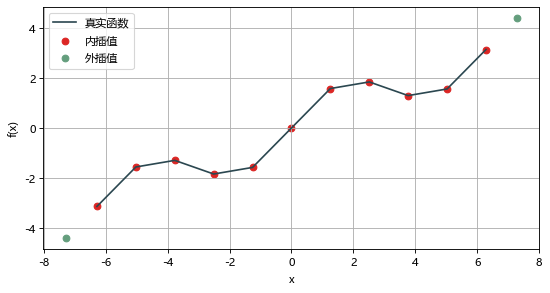
# 外插值设为零spi.splev(x_new, tck, ext=1)
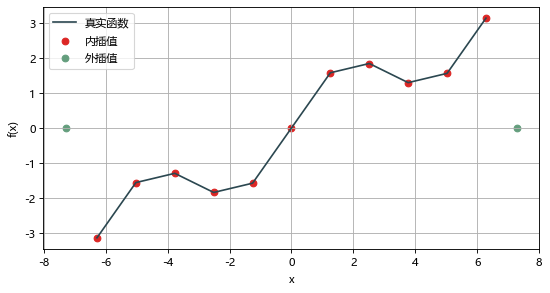
# 平外插spi.splev(x_new, tck, ext=2)
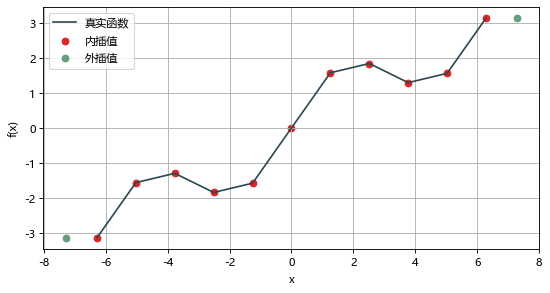
在scipy.interpolate包中除了splrep 和 splev 组合用于插值,还有 interp1d() 插值函数,其函数签名为
interp1d( x, y,
kind='linear',
bounds_error=None,
fill_value=nan )
参数解释如下:
x: 1-D 数值数组,一般是升序排列的数据点
y: N-D 数值数组,插值维的长度必须与 x 长度相同
kind: 字符串或整数,给出插值的样条曲线的阶数,线性插值用 'linear'
bounds_error:布尔值,越界是否报错,除非 fill_value='extrapolate',否则默认越界时报错
fill_value:指定不在 x 范围内时的填充值或填充方法:
填充值 - 元组 (ys, ye) 且 bounds_error=False 时,返回的函数会对小于 x[0] 的值返回元组中第一个元素 ys,对大于 x[-1] 的值返回元组中第二个元素 ye
填充方法 - 字符串 'extrapolate',返回的函数会对落在 x 范围外的值进行线性外插
用 interp1d()三种外插图和上面的三图是一样的。
# 线性外插y = f(x)g = spi.interp1d(x, y, fill_value='extrapolate')y_new = g(x_new)

# 外插值设为零y = f(x)g = spi.interp1d(x, y, fill_value=(0, 0), bounds_error=False)y_new = g(x_new)

# 平外插y = f(x)g = spi.interp1d(x, y, fill_value=(y[0], y[-1]), bounds_error=False)y_new = g(x_new)

一般情况而言,线性外插最合理,但具体用哪种外插要依情况而定。比如外插长端利率用平外插比较保守,线性外插可能查出非常极端的利率。
用下面一组简单数据来举例二维插值。
K = np.array([1, 2, 3]) T = np.array([4, 5])vol = np.array( [[10, 15, 20], [30, 35, 40]] )
K_mat, T_mat = np.meshgrid(K, T)
print(K_mat)print(T_mat)print(K_mat.shape, T_mat.shape, vol.shape)
[[1 2 3]
[1 2 3]]
[[4 4 4]
[5 5 5]]
(2, 3) (2, 3) (2, 3)
上面代码 K_mat,T_mat = np.meshgrid(K,T) 将向量 K 和 T 定义的区域转换成矩阵 K_mat 和 T_mat,其中矩阵 K_mat 的行向量是向量 K 的简单复制,而矩阵 T_mat 的列向量是向量 T 的简单复制。
首先使用 interp2d() 函数但不设置参数 fill_value,那么默认外插的值取最近值。这个“最近”听起来模棱两可,具体解释下图所示。
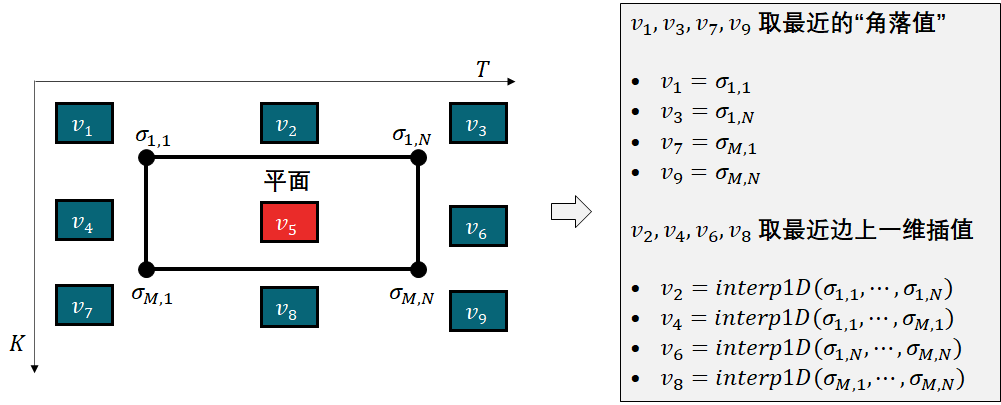
将 K_mat, T_mat 和 vol 传入interp2d() 函数创建对象 g,再向 g 传入新向量 K_new 和 T_new 插出新的 vol 矩阵。
g = spi.interp2d( K_mat, T_mat, vol )K_new = np.array([0.5, 1.5, 2, 2.5, 4])T_new = np.array([3, 4.5, 6])g(K_new, T_new)
array([[10. , 12.5, 15. , 17.5, 20. ],
[20. , 22.5, 25. , 27.5, 30. ],
[30. , 32.5, 35. , 37.5, 40. ]])
验证上面结果:
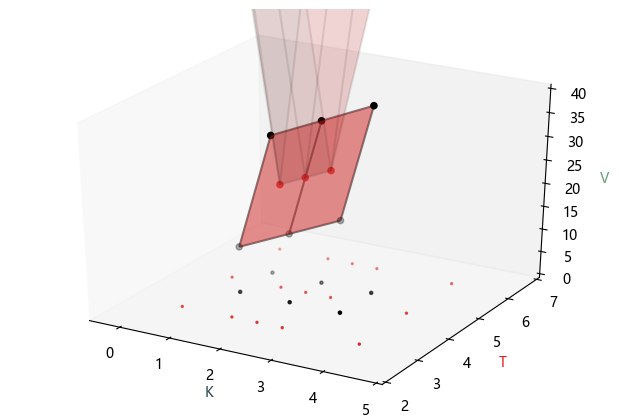
四个顶点值分别是在 (0.5, 3), (4, 3), (4, 6), (0.5,6) 点上外插得到,对应着上图中 v1, v3, v9, v7 的插值规则,即取原平面上最近的“角落值”。
四个边值 (除去顶点) 对应着上图中 v2, v4, v6, v8 的插值规则,即取原平面上最近边上的一维插值。
三个内值都是内插得到的。
将上面结果可视化,如下图所示。黑点是原平面的点,而红点是插值得到的点。
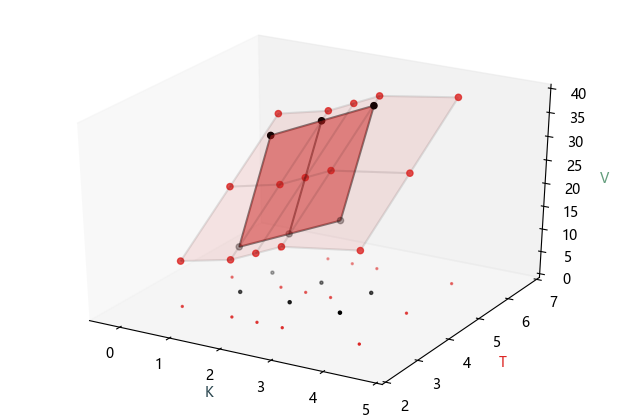
此外在 g 函数可给参数 fill_value 设置具体值,下例将其设为 0,最终插值矩阵的外圈元素都是 0。
g = spi.interp2d( K_mat, T_mat, vol, fill_value=0 )K_new = np.array([0.5, 1.5, 2, 2.5, 4])T_new = np.array([3, 4.5, 6])g(K_new, T_new)
array([[ 0. , 0. , 0. , 0. , 0. ],
[ 0. , 22.5, 25. , 27.5, 0. ],
[ 0. , 0. , 0. , 0. , 0. ]])
将上面结果可视化,如下图所示。
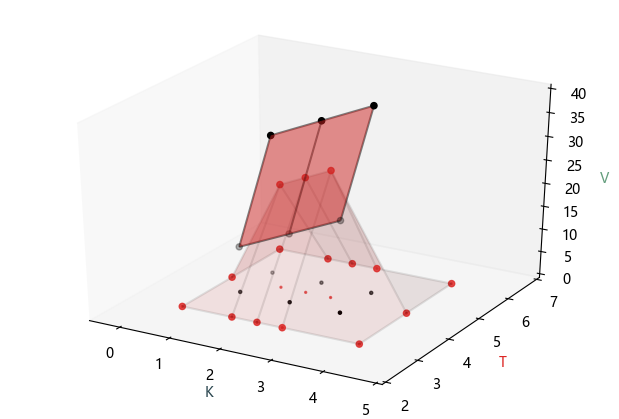
最后展示一下当填充值为 20 和 100 的可视图。
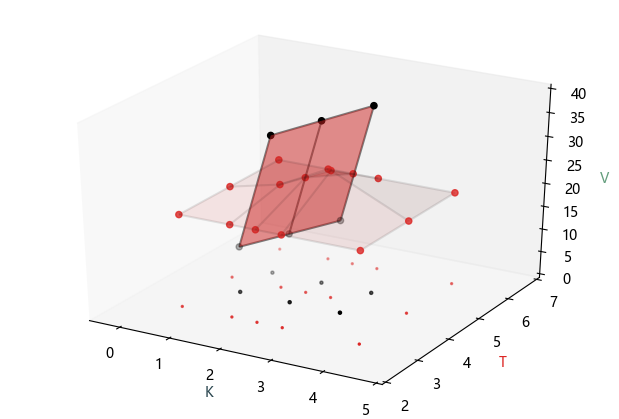
在利率上下限 (interest rate cap/floor) 合约中,买方和卖方将同意以下内容:
买方付出期权金 (premium) 便有权利 (right) 去行使,而卖方收取期权金后则有义务 (obligation) 履行买方行使权利的义务
就未来某段时期 T (1 年至 10 年) 商定一个固定利率 K 作为利率上限/下限
对于上限,买方有权利在每期获得市场利率 L 与上限利率 K 的差额 (L−K)
对于下限,买方有权利在每期获得下限利率
K 和市场利率 L 的差额 (K−L)
而卖方一旦被行使期权时,则有义务支付该差额给买方
其中 L 是 3 或 6 个月的远期利率,那么对应的期 (period) 是 3 或 6 个月。
利率上下限的支付图如下。
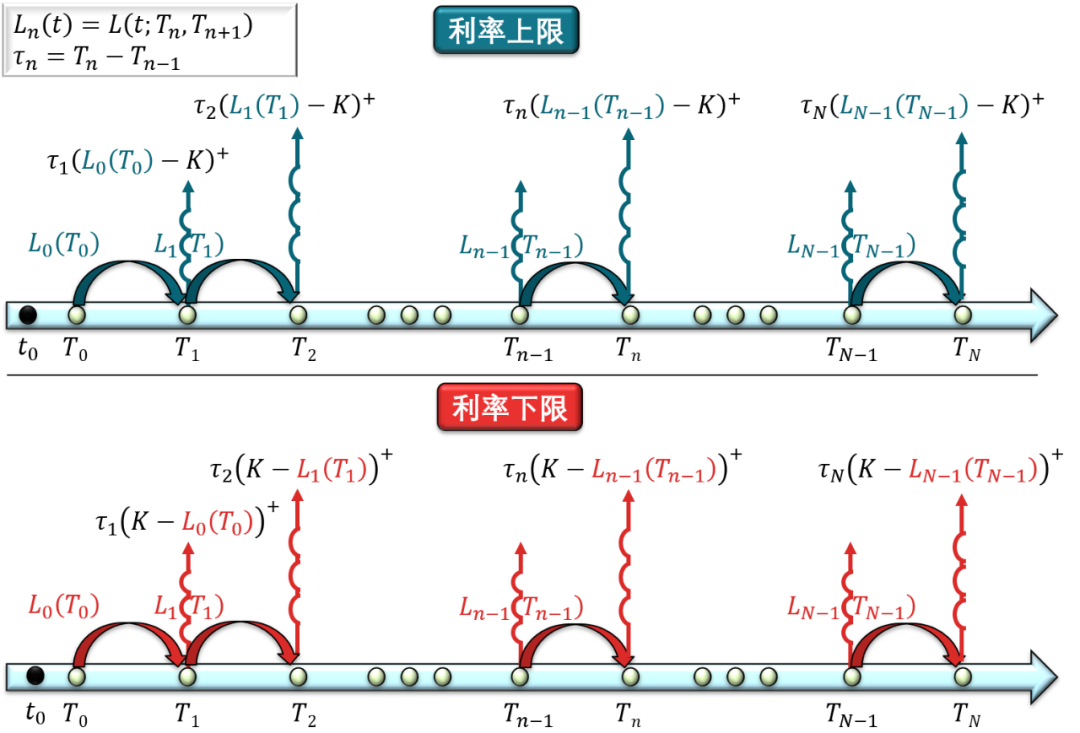
上图定义了利率上限下限的期限结构 (tenor structure)。利率上限下限可分解成一系列的上限下限单元 (caplet/floorlet),其解析解为
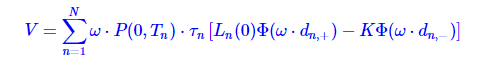
其中
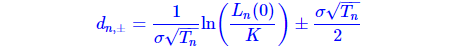
符号 Φ(⋅) 代表标准正态随机变量的累计分布函数 (cumulative distribution function, CDF)。当 ω=1" role="presentation" style=" word-spacing: normal; overflow-wrap: normal; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border-width: 0px; border-style: initial; border-color: initial; box-sizing: content-box; top: 0px; left: 0px; clip: rect(1px, 1px, 1px, 1px); user-select: none; display: inline; transition: none 0s ease 0s; vertical-align: 0px; line-height: normal; height: 1px !important; width: 1px !important; overflow: hidden !important; ">ω=1 时是利率上限,当 ω=−1" role="presentation" style=" word-spacing: normal; overflow-wrap: normal; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border-width: 0px; border-style: initial; border-color: initial; box-sizing: content-box; top: 0px; left: 0px; clip: rect(1px, 1px, 1px, 1px); user-select: none; display: inline; transition: none 0s ease 0s; vertical-align: 0px; line-height: normal; height: 1px !important; width: 1px !important; overflow: hidden !important; ">ω=−1 时是利率下限。
编写定价利率上下限的代码如下:
def BLACK_IRO( F=0.02, K=0.02, D=1, T=0.25, tau=0.25, sigma=0.2, omega=1 ): vol_sqrt_T = sigma*np.sqrt(T) moneyness = np.log(F/K) d1 = moneyness / vol_sqrt_T + 0.5*vol_sqrt_T d2 = d1 - vol_sqrt_T V = omega * D * tau* (F*norm.cdf(omega*d1) - K*norm.cdf(omega*d2)) return np.sum(V)
接下来使用真实市场数据来计算利率上限,首先读取折现曲线和 cap 波动率平面。
curve = pd.read_excel('Market Data.xlsx', sheet_name='Curve', index_col=0)curve.head(3).append(curve.tail(3))
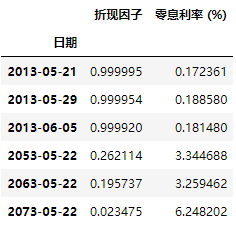
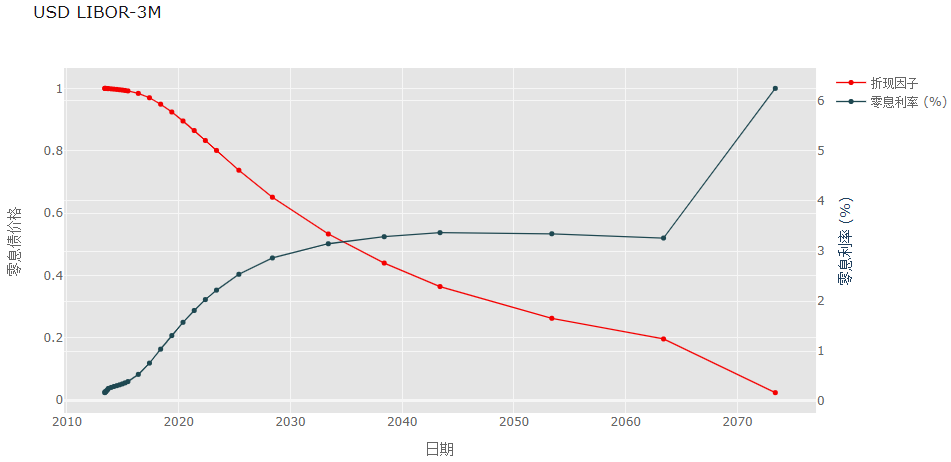
curve.iplot( kind='scatter', mode='lines+markers'
, size=5, title='USD LIBOR-3M', xTitle='日期', yTitle='零息债价格', secondary_y='零息利率 (%)', secondary_y_title='零息利率 (%)', color=color, theme='ggplot' )
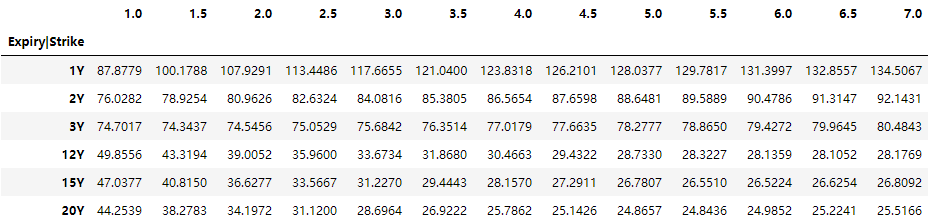
cap_volsurf = pd.read_excel('Market Data.xlsx', sheet_name='CapVol', index_col=0)cap_volsurf.head(3).append(cap_volsurf.tail(3))
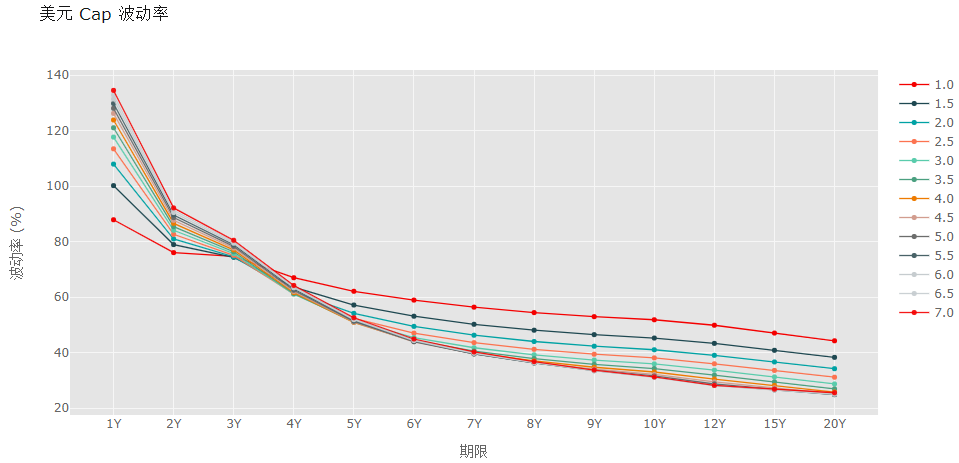
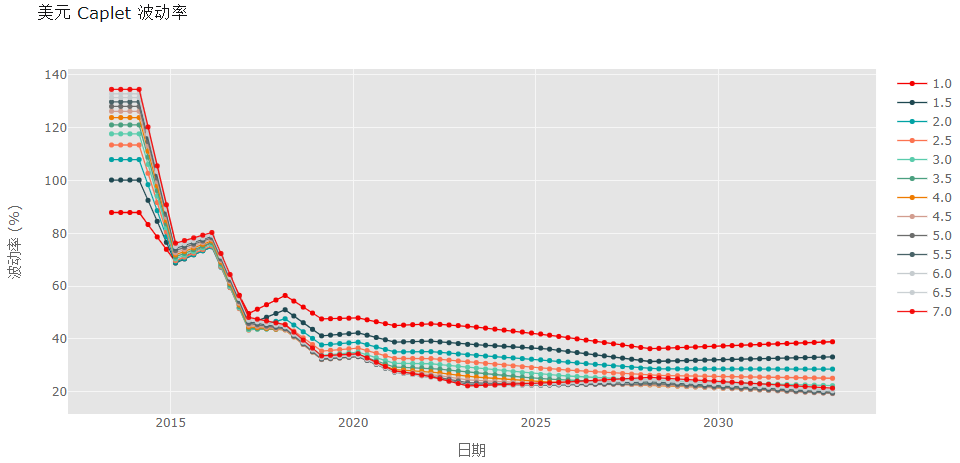
cap_volsurf.iplot( kind='scatter', mode='lines+markers', size=5, title='美元 Cap 波动率', xTitle='期限', yTitle='波动率 (%)', color=color, theme='ggplot' )
但是在 Black 模型中的波动率不是 Cap 波动率,而是 Caplet 波动率,需要一种 CapletStripping 的技巧将 Cap 波动率转换为 Caplet 波动率。这里我们直接用已经转好的 Caplet 波动率。
caplet_volsurf = pd.read_excel('Market Data.xlsx', sheet_name='CapletVol', index_col=0)caplet_volsurf.head(3).append(caplet_volsurf.tail(3))
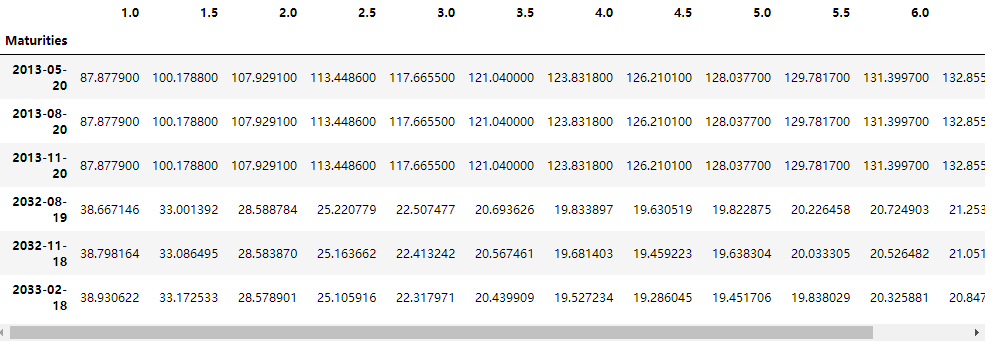
caplet_volsurf.iplot( kind='scatter', mode='lines+markers', size=5, title='美元 Caplet 波动率', xTitle='日期', yTitle='波动率 (%)', color=color, theme='ggplot' )
假设估值日为 2013 年 5 月 20 日,计算一个 5 年的美元利率上限,执行利率为 0.5%,每个 caplet 期限为 3 个月,因此有 20 个 caplet。
today = pd.Timestamp('2013-05-20')date_spot = today + timedelta(days=2)date_cap = [ date_spot+datedelta(months=3*i) for i in np.arange(21) ]K = 0.005
def get_forward_rate( curve, date_s, date_e, today ):
date_curve = pd.DatetimeIndex(curve.index) d_std = (date_curve - today).days.values d_s = (date_s - today).days.values d_e = (date_e - today).days.values tau = (d_e - d_s)/360 tck = spi.splrep( d_std, curve['零息利率 (%)'], k=1 ) r_s = spi.splev( d_s, tck ) r_e = spi.splev( d_e, tck ) DF_s = np.exp(-d_s/365 * r_s/100) DF_e = np.exp(-d_e/365 * r_e/100) F = (1/tau)*(DF_s/DF_e - 1) return F
上面代码 splrep() 和 splev() 的作用是在零息利率曲线上做 1D 线性插值。计算该产品需要的 20 个远期利率。
date_s = pd.DatetimeIndex(date_cap[:-1])date_e = pd.DatetimeIndex(date_cap[1:])F = get_forward_rate( curve, date_s, date_e, today )F

def get_discount( curve, date, today ): date_curve = pd.DatetimeIndex(curve.index) d_std = (date_curve - today).days.values d = (date - today).days.values tck = spi.splrep( d_std, curve['零息利率 (%)'], k=1 ) r = spi.splev( d, tck ) DF = np.exp(-d/365 * r/100) return DF
同理,上面代码 splrep() 和 splev() 的作用是在零息利率曲线上做 1D 线性插值。计算该产品需要的 20 个折现因子。
D = get_discount( curve, date_e, today )D

def get_capletvol( caplet_volsurf, date, K, today ): date_caplet = pd.DatetimeIndex(caplet_volsurf.index) d_std = (date_caplet - today).days.values d = (date - today).days.values K_std = caplet_volsurf.columns.values/100 vol = caplet_volsurf.values/100 K_mesh, d_mesh = np.meshgrid(K_std, d_std) tck = spi.bisplrep( K_mesh, d_mesh, vol ) return spi.bisplev( K, d, tck )
上面代码 bisplrep() 和 bisplev() 的作用是 caplet 波动率平面上做 2D 线性插值。计算该产品需要的 20 个 caplet 波动率。
caplet_sigma = get_capletvol( caplet_volsurf, date_s, K, today )caplet_sigma
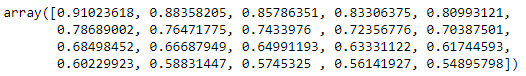
T = (date_e - today).days.values/365T

tau = (date_e - date_s).days.values/360tau

万事俱备只欠东风,将之前所有计算变量结果带入编写好的 Black_IRO() 函数即可。
V_BLK = BLACK_IRO(F, K, D, T, tau, caplet_sigma, 1)V_BLK