discrete convolution:离散卷积
kernel:核
pooling:池化
stride:步长
feature map:特征图
input feature map:输入特征图
output feature map:输出特征图
subsampling:子采样
translated:平移
average pooling:平均池化
max pooling:最大池化
引言
深度卷积神经网络(CNN)一直是深度学习领域取得突飞猛进的核心。尽管CNN早已在九十年代被使用解决字符识别任务(Le Cun等人,1997),然而CNN目前的广泛的应用是由于最近越来越多的工作,如深度卷积神经网络被用来击败ImageNet图像分类挑战中的最新技术(Krizhevsky等,2012)。
卷积神经网络因此构成了机器学习实践者非常有用的工具。但是,第一次学习使用CNN通常是一种令人恐惧的经历。卷积层的输出形状受其输入形状以及核形状(kernel shape),zero padding和步长(stride)的选择的影响,并且推断这些属性之间的关系是很重要的。这与全连接(full-connected)的层相反,其输出大小与输入大小无关。此外,CNN通常还具有池化(pooling)阶段,在全连接的网络方面又增加了一个复杂程度。最后,所谓的反/转置(transposed)卷积层(也被称为fractionally 卷积层)在近来已被用于越来越多的工作中(Zeiler等人,2011; Zeiler和Fergus,2014; Long等人,2015 ; Rad?ford等,2015; Visin等,2015; Im等,2016),并且它们与卷积层的关系已经以不同程度的clarity 进行了解释。
本指南有两个目标:
1.解释卷积层和反卷积层之间的关系。
2.提供在卷积、池化和反卷积层中对输入形状、核形状、zero padding,stides和输出形状之间关系的直观理解。
为了保持广泛的适用性,本指南中显示的结果与实现细节无关,并适用于所有常用的机器学习框架,如Theano(Bergstra等,2010; Bastien等,2012),Torch(Collobert等,2011),Tensorflow(Abadi等,2015)和Caffe(Jia等,2014)。
本章简要回顾了CNN的主要组成部分,即离散卷积(discrete convolutions)和池化(pooling)。有关该主题的深入研究,请参阅《Deep Learning》教科书(Goodfellow等,2016)的第9章内容。
离散卷积
神经网络的The bread and butter是仿射变换(affine transform):接收矢量作为输入,并与矩阵相乘以产生输出(在将结果通过非线性之前,通常添加偏置矢量)。这适用于任何类型的输入,无论是图像,声音片段还是无序的特征集合:无论它们的维度如何,它们的表示都可以在变换之前始终平展到矢量中。
图像,声音片段和许多其他类似的数据具有固有的结构。更规范地说,它们具有一些重要的属性:
• 它们被存储为多维数组。
• 它们具有一个或多个顺序的轴(例如,图像的宽度和高度轴,声音剪辑的时间轴)。
• 一个称为通道(channel)轴的轴用于访问数据的不同视图(例如,彩色图像的红色,绿色和蓝色通道,或立体声音轨的左右声道)
当应用仿射变换时不会利用这些属性; 实际上,所有的坐标轴都以相同的方式进行处理,并且不考虑拓扑(topoligical)信息。尽管如此,利用数据的implicit 结构可能在解决计算机视觉和语音识别等一些任务中非常方便,在这些情况下,最好保留它。这是离散卷积发挥作用的地方。
离散卷积是保留这种排序概念的线性变换(linear transformation)。它是稀疏的(只有少数输入单位对给定的输出单位有贡献)并重用(reuse)参数(相同的权重应用于输入中的多个位置)。
注:原文中的reuses parameters,应该可以理解为shares parameters,即常说的共享参数。
图1.1 介绍了离散卷积的示例。蓝色网格称为输入特征图(input feature map)。为了简化绘图,只显示一个 input feature map,但其实有一个个堆叠在一起的 multiple feature maps也是常见的。核(kernel)在 feature map 上滑动(slide)。在每个位置,计算kernel 的每个元素与其重叠的输入元素之间的乘积,并将结果相加(summed up)以获得当前位置的输出。可以使用不同的 kernels 来重复该过程,以根据需要形成尽可能多的输出特征图(图1.3)。这个过程的最终输出被称为输出特征图(output feature maps)。如果有多个输入特征映射,内核必须是三维的 - 或者等价地,每个特征图将与一个独立的(distinct)kernel 卷积 - 而所产生的特征图将以元素相加以产生输出特征图。
Ps:简单来说,后者等价的意思就input feature map “数量”与 kernel “数量”要一致,目的是为了“数量”个特征图叠加后最终生成一个output feature map。
图1.1 中描绘的卷积是二维卷积(2-D)的一个实例,但它可以推广到N维度(N-D)卷积。例如,在三维卷积(3-D)中,kernel 将是一个长方体(cuboid),并会在input feature map 的高度,宽度和深度(height、wight和depth)上滑动。
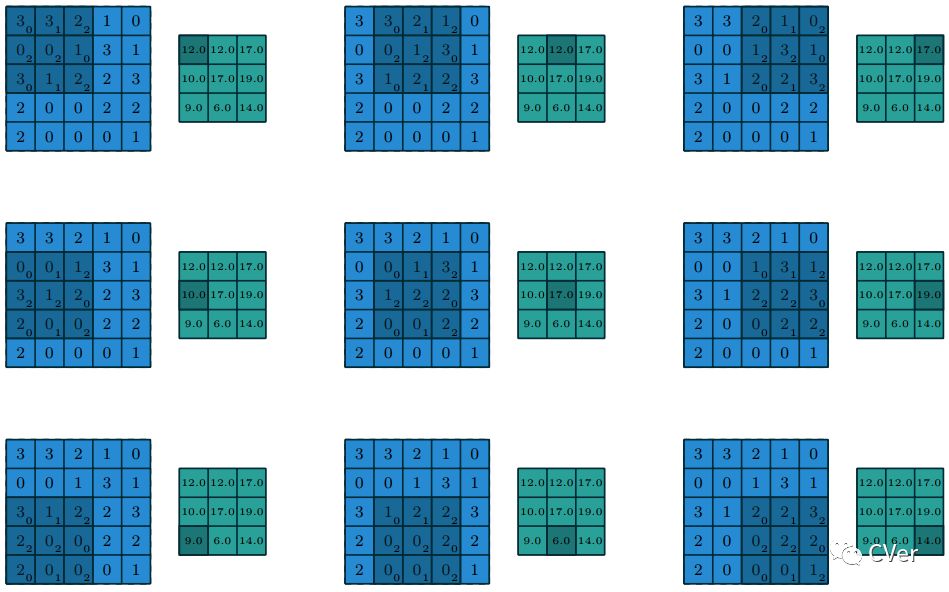
图1.1:计算离散卷积的输出值
定义离散卷积的 kernel 的集合(collection)具有对应于(n,m,k1,...,kN)的一些排列(permutation)的形状,其中:
n = 输出特征图的数量
m = 输入特征图的数量
kj = 沿着 j 轴的 kernel尺寸
以下属性会影响沿 j 轴的卷积层的输出大小 oj:
例如,图1.2 显示了一个将3×3 kernel 应用于填充为1×1的5×5 的输入上,并使用2×2 strides。即k1=k2=3,p1=p2=1,i1=i2=5,s1=s2=2。
请注意,strides 构成了子采样(subsampling)的一种形式。作为被解释为衡量 kernel平移量的一种替代方法,strides也可以看作是保留了多少输出。例如,通过两跳(hops of two)来移动 kernel相当于通过单跳来移动内核,但只保留奇数(odd)输出元素(图1.4)。
注:虽然从信号处理角度看卷积(convolution)和互相关(cross-correlation)存在区别,但在kernel 学习时两者可以互换(interchangedable)。为了简单起见,为了与大多数机器学习文献保持一致,术语卷积(convolution)将用于本指南。其实图像处理中的卷积不是严格意义上的卷积,如没有翻转特性。但对于图像处理来说,经过实验证明,卷积不需要翻转也同样有效。
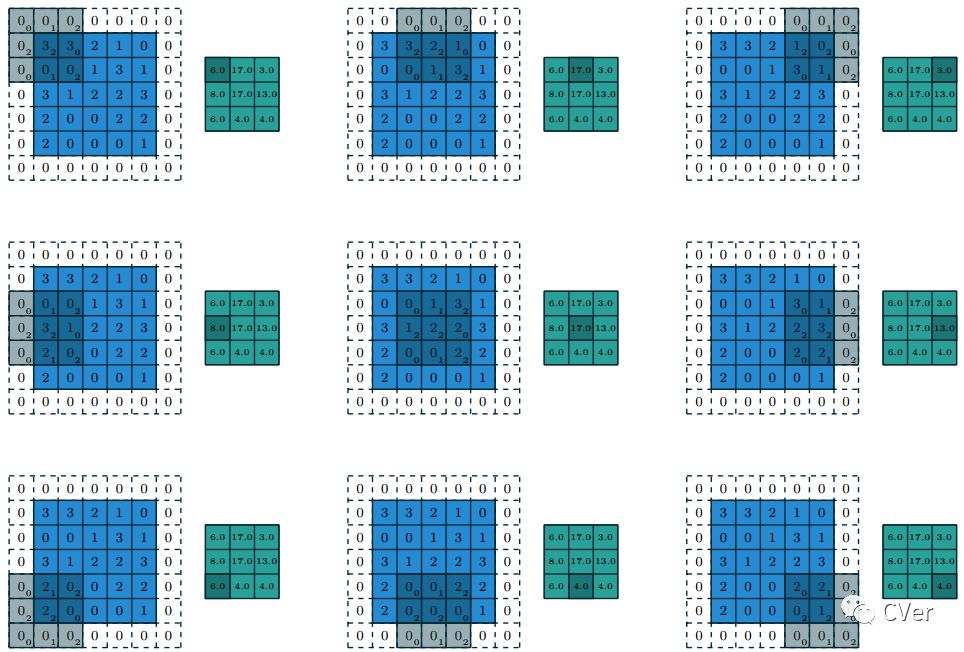
图1.2:二维(N=2)离散卷积的输出值,i1=i2=5,k1=k2=3,s1=s2=2,p1=p2=1。
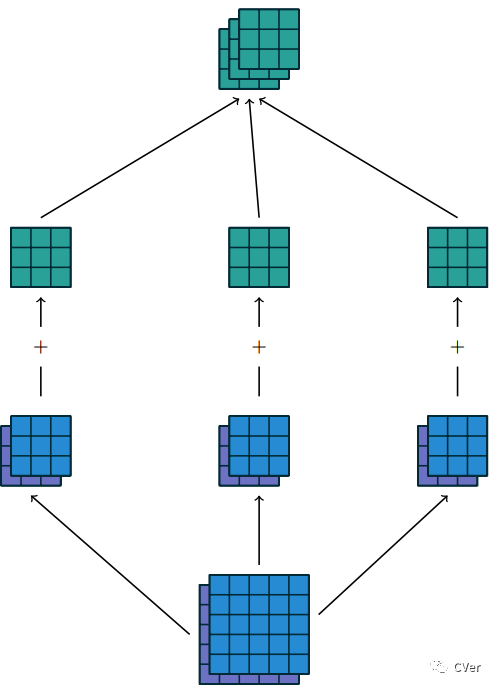
图1.3:使用3×2×3×3 kernel 集合w 将两个输入特征图 卷积 mapping成三个输出特征图。在左列(第1列)中,输入特征图 1(倒数第1行的蓝色)与kernel w1,1(倒数第2行第1列的蓝色)进行卷积,并且输入特征图 2(倒数第1行的紫色)与kenel w1,2(倒数第2行第1列的紫色)进行卷积,并且结果是按照对应元素相加在一起以形成第一个输出特征图(倒数第3行第1列的绿色)。对于中间列(第2列)和右列(第3列)重复上述相同的操作以形成第二个特征图和第三特征图,并且最终将这三个输出特征图“组合”(grouped)在一起以形成最后的输出。
注:一般来说,倒数第2行中每列的蓝、紫 kerel都是不一样的,如倒数第2行第1列的蓝 kernel与倒数第2行的2列的蓝kernel是不一样的,因为这样是为了提取不一样的 feature。
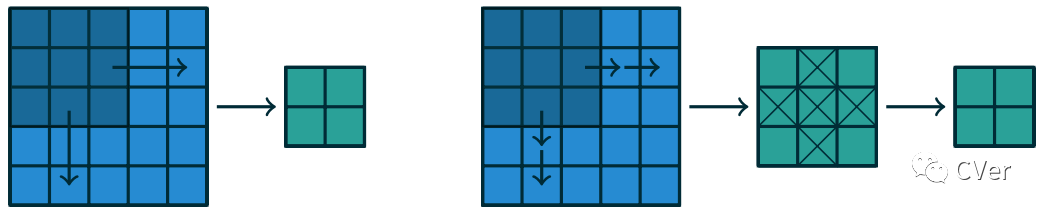
图1.4:另一种观看strides 的方式。不是通过s = 2的增量(左图)来平移(translating)3×3 kernel,而是通过 s=1的增量(increment)来平移 kernel,并且只保留(retained)s = 2个输出元素中的一个(右图)。
池化
除了离散的卷积本身之外,池化(pooling)操作也是 CNN中另一个重要的组成部分。Pooling 操作通过使用某个函数来 summarize子区域(例如取平均值或最大值)以减少特征图(feature maps)的大小。
池化工作是通过在输入上滑动(sliding)一个窗口并将窗口中的内容喂给(feeding)给一个池化函数。从某种意义上讲,池化非常像离散卷积,但是用其它函数替换了由 kernel 描述的线性组合(linear combination)。图1.5 介绍了平均池化(average pooling)的例子,图1.6 介绍了最大池化(max pooling)的例子。
以下属性会影响沿轴 j的池化层的输出大小 oj:

图1.5:使用1x1的 strides在5x5的输入上计算3x3 平均池化(average pooling)操作的输出值。
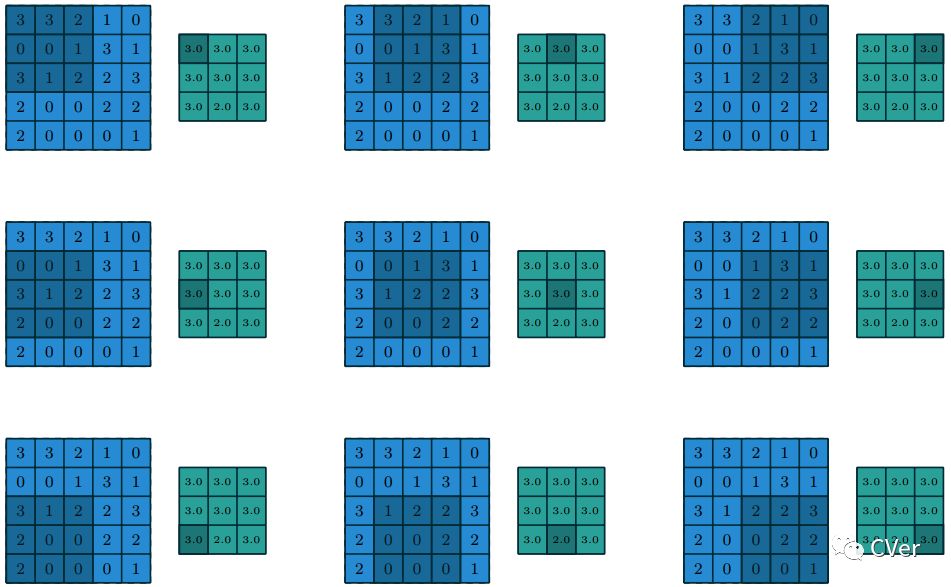
图1.6:使用1x1的 strides在5x5的输入上计算3x3 最大池化(max pooling)操作的输出值。