百度AIStudio源码:  https://aistudio.baidu.com/aistudio/projectdetail/63441

强化学习PARL仓库：https://github.com/PaddlePaddle/PARL

本文提及的源码: https://github.com/kosoraYintai/PARL-Sample/tree/master/eight_puzzle

引言

我们从以下步骤依次着手，带领大家AC并且打败所有的Submissions：

• 可行性分析——为什么可以使用强化学习

• 问题建模——将原问题转化为对应的MDP环境

• DQN的三大改进：DoubleDQN、DuelingDQN、PrioritizedReplayBuffer

• Rainbow模型以及代码实现

• 对比普通DQN以及经典解法

  
  

可行性分析

翻开POJ-1077 ，可以看到一道题，题目大意是这样的。给定初始状态：

以及目标状态：

每次只能移动方格0，有上(U)下(D)左(L)右(R)四个方向可以选择，求由初始状态到达目标状态的最小步数，并打印最优路径。比如对于测试数据，最小步数为3，最优路径为RDR；具体移动步骤如下：

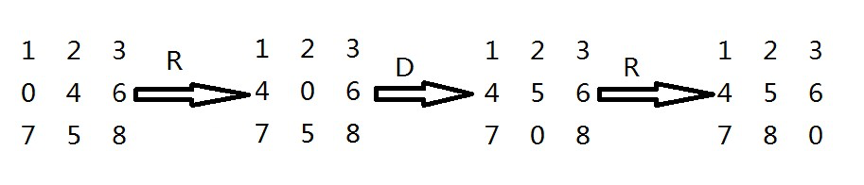
经过初步分析，题目给定了初始状态以及目标状态，相当于有了reset以及terminal；其次，题干中出现了最小、最优等字眼，也就是说，我们需要给出每一步的具体移动方案，这个方案能使得整体的移动步数最少、路径最优，这显然是一个序列决策问题。所以断定：八数码问题可以使用强化学习算法解决。

不妨画出八数码问题的解空间树，节点表示状态State，蓝色表示初始状态，红色表示目标状态，分支上的字母表示动作Action：

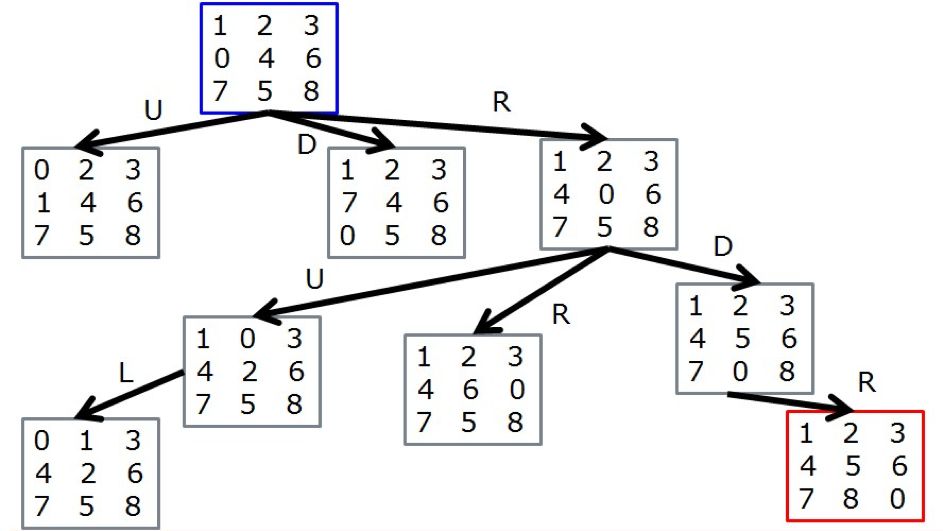
它显然是一个递归的结构，如果在状态State上附加值函数V，在动作Action上附加行为值函数Q，那么就可以转化为V-Q树，采取任意一种强化学习算法，都可以使得每个节点的V、每个分支的Q收敛至最优值，再根据贝尔曼最优方程，就可以推导出整个解空间树的最优解。

另外，由于只能走上下左右四个方向，也就是说每个状态最多可以转化为其他四个状态，而状态s与状态s'之间的相互转化其实是完全对称的(比如s执行L动作可以转化为s'，那么s'执行R动作必然可以转化为s)，所以八数码问题其实建立了一张隐式的无向图；这张无向图是一个稀疏图，每个顶点的度都小于等于4，并且各个顶点都是连通的，我们的目标是求初始状态init_state到最终状态terminal_state的一条最短路径。

问题建模

今天我们所采用的环境比原始的八数码要稍微简洁一些，这道题源自LeetCode的一场周赛weekly-contest-69，输入输出和POJ差不多，只是由八数码变为了六数码，维度变小了而已，题目大意如下。

给定初始状态：

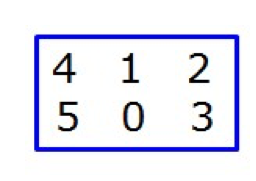
以及目标状态：

求由初始状态变换到目标状态的最小步数，若无解，返回-1；对于测试数据来说，最小步数为5，具体移动步骤如下： 

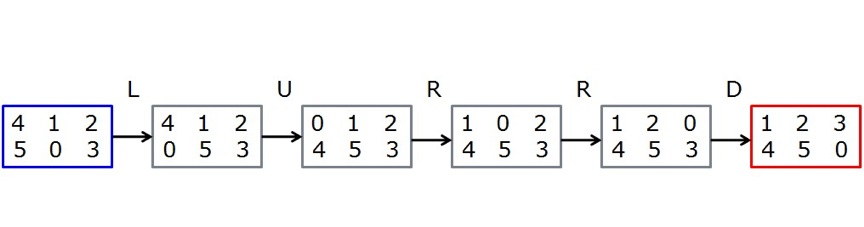
这样做的原因是：

• POJ暂时不支持python，而LeetCode支持Python

• POJ不提供WA和TLE的数据，而LeetCode可以查看哪些用例没有通过，便于我们调试程序

• POJ不提供单个题目的运行时间排名，而LeetCode提供所有AC代码的运行时间分布图，便于我们评测算法的速度

• 在2X3这个benchmark上更容易解释，同理可以推广到3X3的8数码、4X3的12数码等更复杂的问题。

在构建环境之前，我们注意到，无论是POJ还是LeetCode，都提到了可能无解的情况，即：无论怎样移动，都无法到达最终状态。那么什么样的情况有解，什么样的情况无解呢？

我们可以使用逆序对数进行判定，即：首先去除0，再将原始矩阵展开为一维数组，然后判断初始状态和最终状态逆序对数的奇偶性是否一致，如果一致就有解，否则无解。注意到，终止状态的逆序对数为0，恒为偶数，所以只需判断初始状态的是否为偶排列即可。

比如[[1,2,3],[5,4,0]]，展开成一维数组[1,2,3,5,4,0]，去掉0变成[1,2,3,5,4]，其逆序对数为1，是奇排列，所以无解，返回-1

比如[[4,1,2],[5,0,3]]，展开成一维数组[4,1,2,5,0,3]，去掉0变成[4,1,2,5,3]，其逆序对数为4，是偶排列，所以有解，可以进行计算。

关于逆序对数为什么可以判断解的存在性，有兴趣的同学可以解决下LintCode 532，本文提供参考答案，详见ReversPairs.py。

另外，有个小Trick，以上定理仅仅适用于列数为奇数的情况，对于列数为偶数的情况，比如3X2、4X4，每移动一步，排列的奇偶性都会发生改变，这种情况并不是本文的重点。

下面分析一下Environment的核心代码。

EightPuzzleEnv.py：八数码问题的环境，继承自gym.Env，实现了reset、step、reward、render等标准接口。

reset函数：调用initBoard函数初始化一个随机棋盘，并调用findZeroPos找到0所在的位置。

def reset(self):   self.state=initBoard(self.m,self.n,self)  self.pos=findZeroPos(self.state,self.m,self.n)   return self.state

initBoard函数：随机产生一个偶排列，并且这个排列不能和终止状态相同；为了增加初始状态的随机性，这里同时借助于sklearn和numpy两个库。

def initBoard(m,n,env):    '''    初始化一个随机棋盘    '''    MAXITER=65535    for _ in range(MAXITER):        perm=np.arange(m*n)        p=np.random.random()


    
        #随机选择sklearn或者numpy生成一个排列        if p<=0.5:            perm,_= train_test_split(perm,test_size=0)        else:            np.random.shuffle(perm)        #检测逆序对的奇偶性        flag=checkReversePair(perm.copy())        if flag and not np.array_equal(perm, env.target):            return arrayToMatrix(perm, m, n)        else:            continue

step函数：接收参数a，执行上下左右四个动作中的一个，并返回四元组(next_state,reward,terminal,info)；若执行了动作之后如果越界了，则给一个较大惩罚并停让棋子留在原有位置，否则，移动方格，并获得奖励：

def step(self, a):   nowRow=self.pos[0]   nowCol=self.pos[1]   nextRow=nowRow+dRow[a]   nextCol=nowCol+dCol[a]   nextState=self.state.copy()   #检查越界   if not checkBounds(nextRow, nextCol,self.m,self.n) :       return self.state, -2.0, False, {'info':-1,'MSG':'OutOfBounds!'}   #移动方格   swap(nextState, nowRow, nowCol, nextRow, nextCol)   self.pos=np.array([nextRow,nextCol])   #获得奖励   re=self.reward(self.state,nextState)   self.state=nextState   if re==EightPuzzleEnv.SuccessReward:       return self.state, re, True, {'info':2,'MSG':'Finish!'}   return self.state, re, False, {'info':1,'MSG':'NormalMove!'}

render函数：打印当前棋盘，比较简单。

重点分析一下reward函数，也就是奖励怎么设置，因为合理的奖励对于强化学习模型的准确度至关重要。首先，在step函数中，我们已经给予数组越界这种情况一个较大惩罚；其次，到达终点状态显然要给予最大奖励：

#成功回报SuccessReward=10.0if self.isFinish(nextState):    #到达终点，给予最大奖励    return EightPuzzleEnv.SuccessReward

还剩下普通的情况，就是移动方格，我们分析一下以下两种状态：

[[4,1,2],[5,0,3]]，与终点状态[[1,2,3],[4,5,0]] 相比，有6个棋子不一样，其最小移动步数为5

[[1,2,3],[4,0,5]]，与终点状态[[1,2,3],[4,5,0]] 相比，有1个棋子不一样，其最小移动步数为1

所以，用当前状态与终点状态有多少个棋子位置不同来评估当前状态似乎有些道理，不妨把这个标准叫做A_star_dist(A*距离)：

def A_star_dist(target,now):    length=len(now)    cnt=0;    for i in range(0,length):        if target[i]!=now[i]:            cnt+=1;    return cnt

有了这个距离，奖励函数的设置就可以更加合理了。这里我设定了3种不同类型的惩罚，代码实现如下：

#对移动前的棋盘、移动后的棋盘分别进行估价lastDist=A_star_dist(self.target, nowState.ravel())nowDist=A_star_dist(self.target, nextState.ravel())#距离减小，给予较小惩罚if nowDist   return -0.1#距离不变，给予中等惩罚elif nowDist==lastDist:   return -0.2#距离增大，给予较大惩罚else:   return -0.5

那么，是不是每次只要选择使得AStar距离变小的方向进行移动，就一定能得到最优解呢？其实不是的，因为AStar距离的思想和即时奖励一致，它只是对于当前局势的一种估计，做出在当前看来最优的选择，并不一定能使长期回报最大。下文讲到Dueling-DQN的时候，就会举例说明这个现象。

环境差不多构建完了，不妨再构建一个简单的智能体，这个智能体非常的佛系，它完全采取随机的动作。虽然显得很young很naive，但它的作用并不小，用它作为基线，我们不仅可以测试环境的正确性，还可以对数据的分布情况进行统计。

def buddaAgent(env):    return np.random.randint(0,env.ActionDim)

让智能体跑多轮episode，统计到达终点的步数，查看数据分布情况：

if __name__ == '__main__':    env=EightPuzzleEnv(2,3)    #统计到达终点的步数，猜测数据分布    lst=[]    MAX_ITER=2048    for i in range(MAX_ITER):        env.reset()        cnt=0        while True:            a=buddaAgent(env)            nextS,r,terminal,info=env.step(a)            cnt+=1;            if terminal:                break        if i%50==0:            print(i,'stepCnt:',cnt)        lst.append(cnt)    print()    print('min:',np.min(lst))


    
    print('mean:',np.mean(lst))    print('median:',np.median(lst))    print('max:',np.max(lst))    print('std:',np.std(lst))    print('mean divide std:',np.mean(lst)/np.std(lst))

观察一下运行结果：

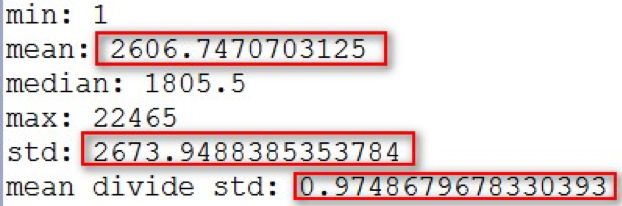
发现均值和标准差非常的接近，而且我们希望用一条连续的曲线来拟合这个分布，正好指数分布也服从均值和标准差相等的性质，不妨建模为指数分布：

def expDist(x, mu):    '''    指数分布    均值和标准差均是:1/λ    '''    landa=1/mu    return landa*np.exp(-landa*x)

使用pyplot可以画出如下曲线，基本上拟合了数据的分布图，效果还是很不错的：

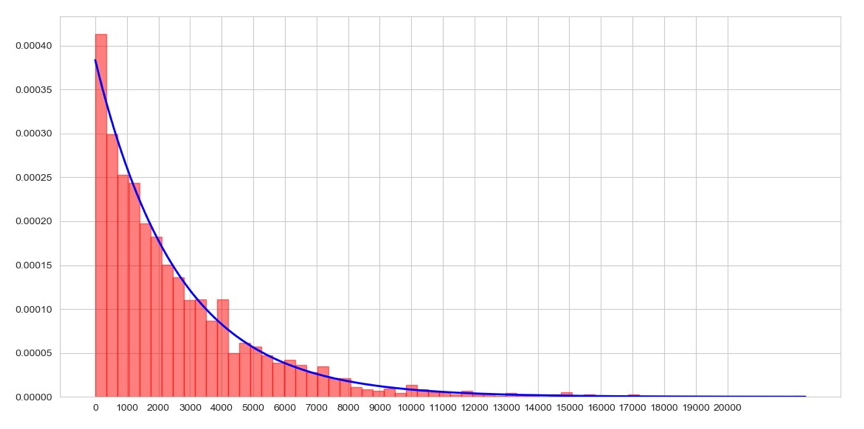
这样做的目的是什么呢？其实是为了确定_max_episode_steps(一轮episode最多执行多少次step)这个阈值；通过观察可以发现，绝大部分数据都分布在均值以下，而且中位数median在2000以下，所以我们可以取个吉利的数字2048作为阈值，这样的话，步数超过这个阈值的episode就可以舍弃，这轮episode中产生的所有数据都可以认为是噪声。

self._max_episode_steps=2048

如果没有这个超参数会发生什么情况呢？试想一下，假设经验池的大小设置为10万，而刚好连续产生了5个步数为2万的episode，那么经验池很快就填满了，这些数据显然不可能是最优解，甚至大部分数据都是离群点或者噪声，把它们喂给模型的话是没有任何意义的，很有可能使模型不收敛；事实上我们更需要采集均值以下、中位数左右的数据作为正常样本，所以有这个限制是很必要的。

看一下TestCase.py，这个程序定义了10个标准的测试用例，将棋盘的初始状态作为特征X，最小步数作为标签Y_True(假设可以经过先验知识得到)：

def testCase():    '''    创建一些测试数据    '''    #棋盘的初始状态作为特征    x=[]    x.append(np.array([[1,2,3],[4,0,5]]))    x.append(np.array([[4,1,2],[5,0,3]]))    x.append(np.array([[1,3,2],[5,4,0]]))    ....    #最小步数作为标签    label=[1,5,16,...]    return x,label

有了测试数据之后，就测试佛系agent的能算出最小步数的准确率了，经过测试可以得到以下输出：

佛系智能体的准确率:0.0%

可以看到，佛系agent的准确率为0，它完全处于人工智障的状态，即使是最简单的[[1,2,3],[4,0,5]]，它甚至也想不到只要往右移动一格就能成功这一步，这样的代码提交到OJ系统显然是要WA的。看来，为了AC掉这道题，训练强大智能体的任务就迫在眉睫了。

Double-DQN

经过这样的变换，模型在过高估计的问题上得到了缓解，稳定性也就得到了提高。

Dueling DQN

Dueling DQN也是DQN的改进算法之一，它的主要突破点在于将神经网络的单一输出分解成两个不同的输出，再将这两个输出进行合并，使得模型能够拥有更好的表现。从架构上来说，这是个一分为二，再合二为一的过程。

这个公式表明，状态行为值函数q可以分解成状态值函数v以及优势函数(Advantage Function)A，这个优势函数A可以反映当前动作比平均价值(或其它动作)好多少的程度：如果优于平均表现，优势函数A为正；反之则为负，表明当前动作不如平均表现好。

有了这样的分解，我们就可以在保持网络主体结构不变的基础上，将原本网络中的单一输出变成两路输出，一个用于输出v，它的维度为1；另一个输出A，它的维度为|Action|，和动作的维度相同。最后将两部分输出结果相加起来，就是原本的q。下图展示了原始DQN结构与Dueling DQN结构的异同：

让每一个A减去当前状态下所有A的均值，就可以满足的期望为0的约束条件，从而增加了v和A输出的稳定性。

这样分解之后有什么好处呢？

首先，通过这样的分解，我们不但可以得到状态行为值函数q，同时还得到了状态值函数v以及优势函数A，那么在某些需要使用v的场景下，就可以直接使用已经训练好的v而不必再训练一个新的网络。

其次，从训练网络的角度来看，原本的DQN需要训练|A|个取值为[0,∞] 的数值，现如今的Dueling DQN需要训练一个取值为[0,∞] 的数值，和|A|个均值为0、取值范围为[-C,C] 的数值，对于训练网络来说，后者显然是更加友好的。

再次，将行为值函数分解后，每一部分的结构都具有实际的意义，我们也可以从中挖掘出有价值的信息。从论文给出的实验结果可以看出，在训练过程中，上下两行图展现不同时刻的V和A，图中红色区域代表V和A所关注的地方。V关注于地平线上是否有车辆出现以及分数，即长期目标；A则更关心会立即造成碰撞的车辆，也就是短期策略的选择。两种策略相互制约、相互促进，使得智能体同时学到了当前最优策略与长期最优回报，训练出来的模型也更容易收敛到最优解。

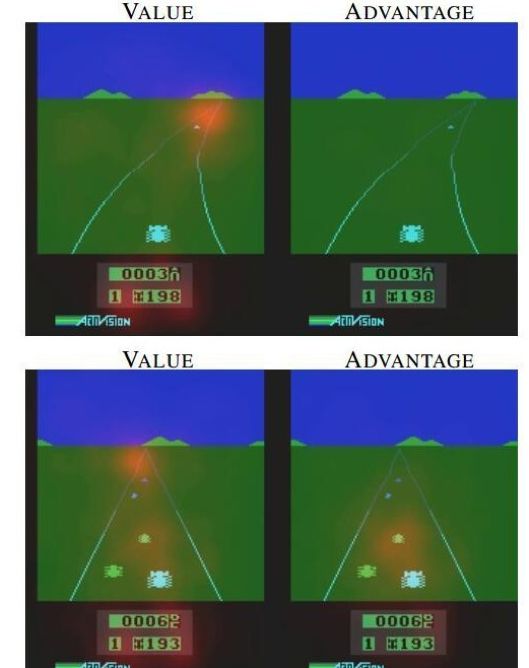
回想一下上文提到的智能体不一定总是选择使得当前AStarDist减小的动作，其实是有道理的，我们看一下[[1,2,4],[5,0,3]] 这个初始状态移动到终止状态的执行过程，假设神经网络已经收敛，可以得到最优解了：

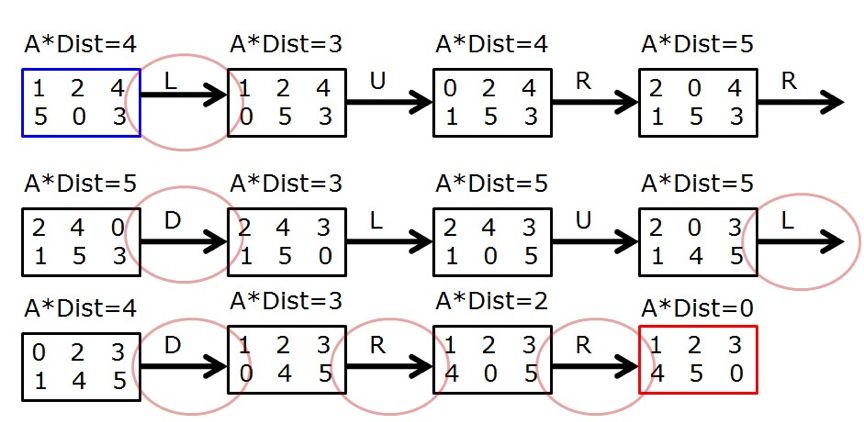
其中，标红圈的表示选择某个动作后使得A*Dist减小的情况，这种情况仅仅占一半左右；其他的移动步骤可能使得A*Dist不变，甚至有可能变大，但总体的移动步数却是最小的。这说明使得AStarDist减小的动作虽然优先考虑，但并不一定总是最优，看来训练八数码问题的时候需要在当前决策和长期决策之间做一定的取舍和平衡，这和Dueling DQN的思想是一致的。

线段树SegmentTree

在了解Prioritized Replay Buffer之前，读者可以试一试能否AC这两道题：LeetCode 307，POJ 3264，前者是RangeSumQuery(区间和查询问题)，后者是RMQ(Range Min/Max Query，区间最值问题)，这两道题都用到线段树的知识。

线段树SegmentTree是一种高效的数据结构，它可以在O(logN)时间内完成修改和查询操作。

举个例子，假设我们需要求数组[2, 5, 1, 4, 9, 3] 的区间最小值，那么就可以使数组中的每个元素拥有四个域：node_Index表示节点在树中的下标，i表示区间的开始位置，j表示区间的结束位置j，value表示区间最小值；于是可以构造如下二叉树：

具体代码实现，读者可以参考OpenAI的项目Baselines，baselines/common/segment_tree.py中的__setitem__以及_reduce_helper函数。

Prioritized Replay Buffer

我们知道，普通DQN使用了经验回放机制，在训练模型的时候对Replay Buffer进行随机采样，打破了样本之间的相关性，并提高了样本的利用率。那么这种以均匀策略进行采样的方式一定合理吗？其实不一定，因为每一个样本所占权重不一样，难度也不一样。有的样本相对简单，学习得到的收获不会太高；有的样本则有些困难，经过学习后会对模型产生较大的帮助。如果平等地看待每一个样本，那么就会在那些简单的样本上花费较多的时间，而学习的潜力并没有被充分挖掘出来。

Prioritized Replay Buffer就很好的解决了这个问题，它打破了均匀采样，赋予学习效率高的样本更大的采样权重。如何选择权重呢？一个理想的标准就是将TD-Error，也就是δ作为权重，如果TD-Error越大，说明该状态处的值函数与TD目标的差距越大，神经网络参数的更新量就越大，因此该样本的学习效率越高。并且，如果一个样本是新产生的，我们期待它可以被多次训练，于是可以赋予新加入经验池的样本一个较大的权重。

那么直接使用TD-Error作为权重合理吗？其实不是很合理，因为不同的样本直接的TD-Error可能差距很大，比如某个样本的TD-Error为100，另外一个样本的TD-Error为0.01，那么0.01的这个样本基本上不会被采样到，这样模型很容易过拟合，所以我们需要追求：确保TD-Error较高的样本被采样的次数较多，同时也要使得那些TD-Error较低的样本以一定的概率被采集到。

于是解决的办法是这样的，定义样本采样概率的计算公式为：

其中priority(i)表示样本的采样概率，p(i)表示每个样本所占总δ[zhoubo1]  的比例，α可以调整样本δ的重要性。当α=1时，相当于直接使用δ的数值；当α<1时，就可以削弱较高TD-Error样本的影响，增加低TD-Error样本的采样效率，使得采样过程更加合理。

有了优先级priority，为了有效地获取priority较高的样本，SumTree就派上用场了。

SumTree的节点存储的是区间[i,j]的和，为了方便，我们举一个满二叉树的例子，这个二叉树存储了数组[3,10,12,4,1,2,8,2] 的区间和，有8个叶子节点，节点总数为：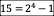

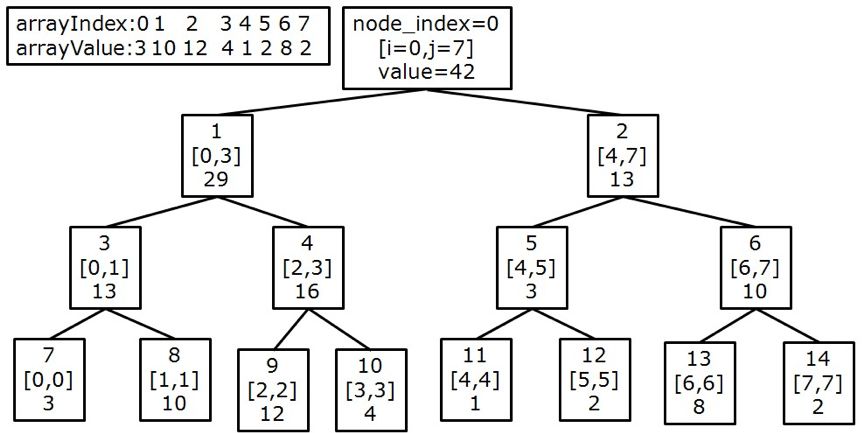
除了普通的RangeSumQuery之外，还有第二种查询方式——前缀和查询。

前缀和sum[i]的定义为：数组0位置到i位置的所有元素的和；请查找寻找前缀和sum[i-1]小于等于v的最大下标i。

可以使用SumTree快速求解这个问题，它的基本思想是这样的：

• 比较当前要查询的前缀和v与节点左子树leftV的大小

• 若leftV⩾v，则在左子树中继续查询v

• 否则，用v减去leftV，并在右子树中继续查询v-leftV

• 重复执行以上过程，直到遇到叶子节点

举个例子，假设需要查询的前缀和为23，过程如下：

• 比较23与根节点的左子树(1号节点)的大小，发现29>23，则进入左子树(1号节点)继续查询23

• 比较23与左子树(3号节点)的大小，发现13<23，则23-13=10，进入右子树(4号节点)继续查询10

• 比较10与左子树(9号节点)的大小，发现12>10，而12又是叶子，故算法停止，返回9号节点作为结果，其对应的数组下标为2，数组的值为12

经过检测可以发现：3+10=13<23，而3+10+12=25>23，故结果正确。

下图展示了查询的过程，标蓝的部分为每次查询的值，标红的部分为本次查询所经过的路径：

显然，整个查询过程会形成从根节点到叶子节点的一条完整路径，所以时间复杂度为O(logN)，代码实现可以参考官方baselines/common/segment_tree.py中的find_prefixsum_idx函数。

实际进行抽样时，将根节点的priority作为总和sum，除以batch_size，分成batch_size个大致相等的区间。如上图所示，所有node的priority加起来是42，假设抽7个样本，这时priority区间的分布就是这样：[0,6]，[7-12]，[13-18]，[19-24]，[25,30]，[31,36]，[37,42]。然后在每个区间里使用均匀分布产生一个随机数，并进行前缀和的查询。

注意到，虽然产生的随机数是均匀的，但每个节点的采样权重并不均匀，甚至有可能存在横跨多个区间的节点(比如9号节点的优先级为12，所占区域为[13-25]，横跨[13-18]、[19-24]两个区间，对这两个区间进行采样的时候，9号节点都是100%会被选到的)，所以优先级越大的节点越有可能被选到，这样就能完成优先级采样的过程。下图的蓝色框表示每个叶子节点所占的区域：

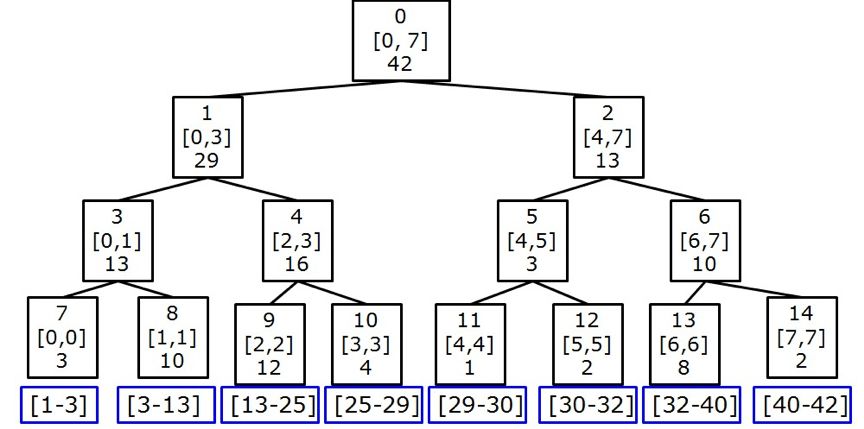
这样，优先级采样的功能似乎已经完成了，但可能有同学注意到刚才的这样一个Trick：

每个节点的采样权重并不均匀，甚至有可能存在横跨多个区间的节点

是的，优先级越大的节点越有可能被选到，也就是说，Prioritized Replay Buffer的样本是非等概率取出的，甚至在极端情况下，有可能一个bacth_size中出现多个重复的样本，这显然是一个有偏估计，可能会使模型欠拟合。为了矫正这个偏差，使得模型的训练变的无偏，可以给每个样本的乘以一个重要性采样系数：

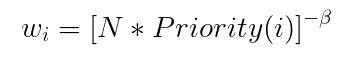
其中，N表示Replay Buffer中的样本数量，Priority(i)表示样本的采样优先级，β是介于(0,1]之间的一个数。这个权重系数Weight表示当前样本对梯度更新的影响，样本的优先级Priority越大，Weight就越小，这样就削弱了采样优先级较高的样本对梯度更新以及loss函数的影响。β一开始是小于1的某个超参数，随着迭代次数的增加，让β不断变大，逐渐接近1，最后效果就等同于普通的Replay Buffer，这样既能提升样本的利用率，又能确保结果不会带来太大的偏差。

SegmentTree.py的sample函数，就实现了优先级采样、计算重要性采样权重两个功能，其中，重要性采样系数Weight的计算既可以使用原始公式，也可以使用另外一个公式：

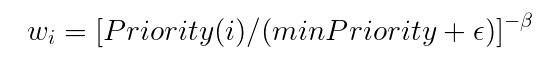
它俩是等效的，并无实质性差别：

def sample(self, n):#根据采样优先级Priority进行采样，并计算重要性采样系数Weight    b_idx, b_memory, ISWeights = np.empty((n,), dtype=np.int32), [], np.empty((n, 1))    #平均分成n个区间,每个区间的大小为pri_seg    pri_seg = self.tree.total_p / n    self.beta = np.min([1., self.beta + self.beta_increment])    min_prob = np.min(self.tree.tree[-self.tree.capacity:]) / self.tree.total_p      for i in range(n):        a, b = pri_seg * i, pri_seg * (i + 1)        #使用均匀采样的方式，随机产生[a,b]区间的某一个数        v = np.random.uniform(a, b)        #使用SumTree的查询进行采样        idx, p, data = self.tree.get_leaf(v)        #计算采样优先级Priority        priority = p / self.tree.total_p      #计算重要性采样权重Weight,用于训练阶段,削弱较高优先级样本对梯度更新、loss函数的影响        #ISWeights[i, 0] = np.power(priority*self.tree.size, -self.beta)        ISWeights[i, 0] = np.power(priority/(min_prob+1e-4), -self.beta)        b_idx[i] = idx        b_memory.append(data)    return b_idx, b_memory, ISWeights

Rainbow模型以及代码实现

主角Rainbow终于登场了，它将DQN的几种改进算法融合在了一起，是基于集成学习(Ensemble Learning)思想的一种模型。今天我们就尝试着扩展一下PARL的Algorithm层，并将前面的Double DQN、Dueling DQN、Prioritized Replay Buffer整合成新的强化学习模型——Rainbow。

关于DQN的改进算法，还有Multi-step Learning、Distributional Network、Param Noise等等，并不在本文的讨论范围之内，有兴趣的读者可以查阅其它资料。

依次分析replay_memory、env、model、algorithm、agent、train等模块

1、SegmentTree.py：里边有SumTree和Memory两个类；SumTree前面已经分析过了，Memory类里边最重要的函数sample(实现优先级采样、重要性采样系数计算两个功能)也已经分析过了，还剩下一些超参数。

#微小扰动，防止除0错误epsilon = 0.01#将TD-Error转化为优先级priority,使得较低优先级的样本也可以被采集到alpha = 0.6#超参数,用于重要性采样,初始值小于1,最后逐渐增长到1beta = 0.3#用于归一化TD-Errorabs_err_upper = 1.0#超参数，beta的增长速率beta_increment=2e-6

store函数：用于存储样本，注意将新样本的优先级设置为最大值。

def store(self, transition):    max_p = np.max(self.tree.tree[-self.tree.capacity:])     if max_p == 0:        max_p = self.abs_err_upper     #将新添加的数据的优先级设置为最大值     self.tree.add(max_p, transition)

batch_update函数：进一步封装了SumTree的update，用于批量更新优先级，由于样本训练之后TD-Error会产生变化，所以每训练一批样本，这个函数都会被调用。

def batch_update(self, tree_idx, abs_errors):     abs_errors += self.epsilon     clipped_errors = np.minimum(abs_errors, self.abs_err_upper)     ps = np.power(clipped_errors, self.alpha)     for ti, p in zip(tree_idx, ps):         self.tree.update(ti, p)

2、FcPolicyReplayMemory.py：经验池，用于存储交互过程中产生的(state, action, reward, terminal,next_state) 这个五元组。

今天我们使用PriorityReplayMemory这个类，它封装了SegmentTree.py中的Memory类，有append、updatePriority、size、sample_batch等功能，其中append用于添加新样本，updatePriority封装了memory的batch_update方法，size返回经验池的当前大小，这三个函数都非常简单。sample_batch函数用于优先级采样，它调用了Memory的sample方法，比普通的Replay Memory返回的五元组多了两个字段，一个是重要性采样权重weights，另外一个是样本在SumTree中的下标tree_index：

def sample_batch(self, batch_size):    tree_index, batch_memory, is_weights = self.memory.sample(batch_size)    state = np.zeros((batch_size, ) + self.state_shape, dtype='float32')    action = np.zeros((batch_size, ), dtype='int32')    reward = np.zeros((batch_size, ), dtype='float32')    isOver = np.zeros((batch_size, ), dtype='bool')    nextState = np.zeros((batch_size, ) + self.state_shape, dtype='float32')          weights = np.zeros((batch_size, ), dtype='float32')    for i in range(0,len(batch_memory)):        exp=batch_memory[i]        state[i]=exp.state        action[i]=exp.action        reward[i]=exp.reward        isOver[i]=exp.isOver        nextState[i]=exp.nextState        weights[i]=is_weights[i]    return [state, action, reward, isOver,nextState,weights,tree_index]

3、ReversePairs.py：使用归并排序求逆序对数；上文已经分析过了。

4、TestCase.py：生成一些标准的测试用例；上文已经分析过了。

5、EightPuzzleEnv.py：八数码问题的环境；上文已经分析过了。

6、PuzzleDuelingModel.py：神经网络模型，有两个隐藏层，维度都是64，激活函数选用tanh；有两个出口，分别是状态值函数V、优势函数A，然后计算A的均值，再用A减去均值加上V就得到状态行为值函数Q，最后将Q作为神经网络的输出。

class PuzzleDuelingModel(Model):    def __init__(self, act_dim):        self.act_dim = act_dim        self.fc0=layers.fc(size=64,act='tanh')         self.fc1=layers.fc(size=64,act='tanh')        #状态值函数V        self.valueFc = layers.fc(size=1)        #优势函数A        self.advantageFc = layers.fc(size=act_dim)            def value(self, obs):        out = self.fc0(obs)        out = self.fc1(out)        V=self.valueFc(out)        advantage=self.advantageFc(out)        #计算优势函数的均值,用于归一化       advMean=fluid.layers.reduce_mean(advantage, dim=1, keep_dim=True)        #状态行为值函数Q=V+A        Q = advantage + (V - advMean)        return Q

7、pddqn.py ：算法层，是本文的核心内容之一；pddqn是Priority_Double_DQN的简写，继承自PARL官方的Algorithm，主要重写了define_learn函数，在原始dqn.py的基础上加入了三个新功能：

• Double DQN方式的参数更新

• 接受样本的训练权重weight，将weight作为loss函数以及梯度更新的系数

• 不仅要返回cost，而且要返回新的TD-Error

define_learn函数的代码如下：

def define_learn(self, obs, action, reward, next_obs, terminal,weight):     #Q(s,a|θ)    pred_value = self.model.value(obs)     #Q(s',a'|θ')    targetQ_predict_value = self.target_model.value(next_obs)     #Q(s',a'|θ)    next_s_predcit_value = self.model.value(next_obs)     #argMax[Q(s',a'|θ)]    greedy_action = fluid_argmax(next_s_predcit_value)     predict_onehot = fluid.layers.one_hot(greedy_action, self.action_dim)     #Q(s',argMax[Q(s',a'|θ)]|θ')    best_v = fluid.layers.reduce_sum(fluid.layers.elementwise_mul(predict_onehot, targetQ_predict_value),dim=1)    best_v.stop_gradient = True    #TD目标: R+γ*Q(s',argMax[Q(s',a'|θ)]|θ')    target = reward + (1.0 - layers.cast(terminal, dtype='float32')) * self.gamma * best_v    action_onehot = layers.one_hot(action, self.action_dim)    action_onehot = layers.cast(action_onehot, dtype='float32')    pred_action_value = layers.reduce_sum(           layers.elementwise_mul(action_onehot, pred_value), dim=1)            #计算新的TD-Error    newTd = layers.abs(target - pred_action_value)    cost = layers.square_error_cost(pred_action_value, target)    #weight表示样本的权重，影响cost的更新幅度    cost=weight*cost    cost = layers.reduce_mean(cost)    optimizer = fluid.optimizer.Adam(self.lr, epsilon=1e-3)    optimizer.minimize(cost)    return cost,newTd

可以看到，通过继承parl.Algorithm，我们很方便地定义自己的算法。

正是由于PARL具有可读性好、可扩展性高、可复用性强等优点，才使得用户能够非常方便的实现新的强化学习算法！

8、PrioritizedAgent.py，智能体agent层；其中，build_program、sample、predict这几个函数的写法与普通DQN类似；唯一不同的是learn函数，它比普通DQN多了一个weight参数，接收六元组(obs, act, reward, next_obs, terminal, weight) 完成学习功能，返回值也多了newTd，表示新的TD-Error

def learn(self, obs, act, reward, next_obs, terminal,weight):    if self.global_step % self.update_target_steps == 0:        


    
self.alg.sync_target(self.gpu_id)    self.global_step += 1    act = np.expand_dims(act, -1)    if self.clip_reward:        reward = np.clip(reward, -1, 1)    feed = {        'obs': obs.astype('float32'),        'act': act.astype('int32'),        'reward': reward,        'next_obs': next_obs.astype('float32'),        'terminal': terminal,        'weight':weight    }    cost,newTd = self.fluid_executor.run(        self.learn_program, feed=feed, fetch_list=[self.cost,self.newTd])    return cost[0],newTd

除此之外，还多了一个新的超参数clip_reward，用来决定是否归一化即时奖励。

#是否归一化奖励,超参数可微调self.clip_reward=False

通常情况下，常用的做法是把所有即时奖励进行归一化；但是对于八数码问题来说，由于最终状态获得的即时奖励对整个过程影响较大，为了使得这个奖励能够更快的传递到之前的所有状态，所以不进行归一化也是有道理的，可能会加速模型的收敛，后期我们测试一下这个超参数的影响。

9、TrainTest_Rainbow.py，训练与测试，让环境evn与智能体agent进行交互。

首先看一下init_rainbow，这个函数用于构建rainbow模型，初始化环境-environment、神经网络-model、算法-algorithm、智能体-agent以及优先级经验池-PrioritizedReplayBuffer：

def init_rainbow():    #构建环境    env = EightPuzzleEnv()    #动作维度    action_dim = 4    #超参数    hyperparas = {        'action_dim': action_dim,        #学习率        'lr': LEARNING_RATE,        #奖励衰减系数        'gamma': GAMMA    }    #model表现为Dueling-DQN    model = PuzzleDuelingModel(act_dim=action_dim)    #Double-DQN 的功能在algorithm中实现    #Prioritized_Replay_Buffer的功能由algorithm+agent+ReplayMemory共同组成    algorithm = PDDQN(model, hyperparas)    agent = PrioritizedAgent(algorithm, action_dim)    rpm =PriorityReplayMemory(max_size=MEMORY_SIZE, state_shape=StateShape)    return env,agent,rpm

其次，看一下run_train_episode，这个函数用于训练一轮episode，和普通DQN的训练方式相比，有两个主要改进：

• 普通DQN采集的样本是五元组，而这里是一个七元组(s, a, r, terminal, s', weight, tree_index)，其中weight表示重要性采样的权重，tree_index表示样本对应SumTree中的节点下标；并且，在训练之后，还需通过新的δ批量更新样本的采样优先级。

#采集的样本是一个七元组batch_state, batch_action, batch_reward, batch_isOver,batch_next_state,batch_weight,tree_index= rpm.sample_batch(batchSize)#执行SGD,训练参数θcost,newTd = agent.learn(batch_state, batch_action, batch_reward,batch_next_state, batch_isOver,batch_weight)#通过新的TD-Error更新采样优先级rpm.updatePriority(tree_index,newTd)

• 二级缓存L2Cache；在环境执行step之后，并不是马上将五元组存入ReplayBuffer，而是先存入二级缓存。当本轮episode结束后，判断本轮episode是否到达终止状态，如果到达，则将二级缓存中的数据复制进ReplayBuffer；否则，说明总步数大于阈值_max_episode_steps，那么就将本轮的样本当做噪声全部舍弃。

#二级缓存L2Cache，存储本轮的数据L2Cache=[]...    #执行动作    next_state, reward, isOver,_ = env.step(action)    step += 1    #将五元组(s,a,r,terminal,s')加入二级缓存    L2Cache.append(Experience(state.ravel(), action, reward, isOver,next_state.ravel()))...##过滤掉步数大于_max_episode_steps的episode,并将二级缓存中的数据复制到经验池if L2Cache[-1].isOver==True:    for exp in L2Cache:        rpm.append(exp)

除了这两个改进之外，其他的逻辑和普通DQN相差无几。

然后，我们再看一下超参数以及日志记录的部分。其中，MEMORY_SIZE、UPDATE_FREQ、TOTAL、logFreq等超参数和普通DQN的写法完全一致。除此之外，有两个指标评价模型的好坏，分别是平均奖励、平均步数；平均奖励很好理解，模型越优，平均奖励越大；由于八数码问题需要求解最小步数，所以平均步数越小，模型越优：

#记录平均奖励meanReward=0#记录平均步数meanEpStep=0

另外，我们可以将平均步数以及平均奖励保存至文件，后期绘制成学习曲线，就可以对比Rainbow模型和普通DQN的训练效率：

#平均奖励的学习曲线reward_curve=[]#平均步数的学习曲线step_curve=[]#保存学习曲线nowDir = os.path.dirname(__file__)parentDir = os.path.dirname(nowDir)np.savetxt(parentDir+'/learning_curve_log/rainbow_reward.txt',reward_curve,fmt='%.3f')np.savetxt(parentDir+'/learning_curve_log/rainbow_step.txt',step_curve,fmt='%.3f')

最后，为了测试模型的准确率，可以将TestCase.py里的标准数据作为测试集，并用训练好的模型对测试集进行检验，若步数一致，输出"Accepted!"，表示预测正确，若步数不一致，输出"Wrong Answer!"，表示预测失败。这样的话，就相当于通过监督学习的方式统计出准确率Accuracy。moveDirection表示移动的箭头，也就是上下左右，有了它，我们就可以查看智能体每一步所采取的具体策略了：

#移动的箭头moveDirection={0:'↑',1:'↓',2:'←',3:'→'}...x,correctList=testCase()okCnt=0for i in 


    
range(len(x)):    board=x[i]   correctCnt=correctList[i]   isOk=run_test_episode(env, agent,board,correctCnt)      if isOk:         okCnt+=1print('准确率:{:.1f}%'.format(okCnt/len(x)*100))

运行main函数，输入train进行训练，输入test进行测试。在这里我们输入train，经过一段时间的训练之后，可以看到如下输出日志(这里仅仅取一个样本进行观察)：

对于[[1,2,4],[5,0,3]] 这个初始状态，智能体使用了11步走到了终点，预测值和真实值一样，而且动作也显示正确。再看一下最后一行的输出：

准确率:100.0%

说明模型在测试集上表现良好，对于每一条测试数据，都能准确无误的找到最小步数和最优路径。

看一下AutoWriteCode_Rainbow.py，这个程序用于自动写代码和统计数据分布，分为以下几个步骤：

1、利用随机数发生器生成所有的初始状态，这样做的好处是代码里边的静态表是随机打乱的，从而排除了被检测到作弊的可能

2、使用已经训练好的模型生成所有的解，并存入一个map，map的key为初始状态，value为步数

3、遍历map，就可以打一个静态表，并生成可执行的python程序，write_ac_code函数就实现了这个功能：

def write_ac_code(dic):    '''    自动写AC代码    '''    print()    print('''def boardToKey(board):    key=""    for array in board:        for i in array:            key+=str(i)    return key    ''')        print('''class Solution:    def slidingPuzzle(self, board: List[List[int]]) -> int:''')    print('        d={}')    for entry in dic.items():        print('       d["'+entry[0]+'"]='+str(entry[1]))    print('        key=boardToKey(board)')    print('''        if key in d:            return d[key]        else:            return -1''')

4、由于我们并不知道数据的真实值，所以在提交代码之前，可以统计一下预测值的数据分布情况，看看是否符合常理，使用pyplot实现这个功能。

看一下控制台的输出，经过2200多次的迭代，终于自动写完了代码：

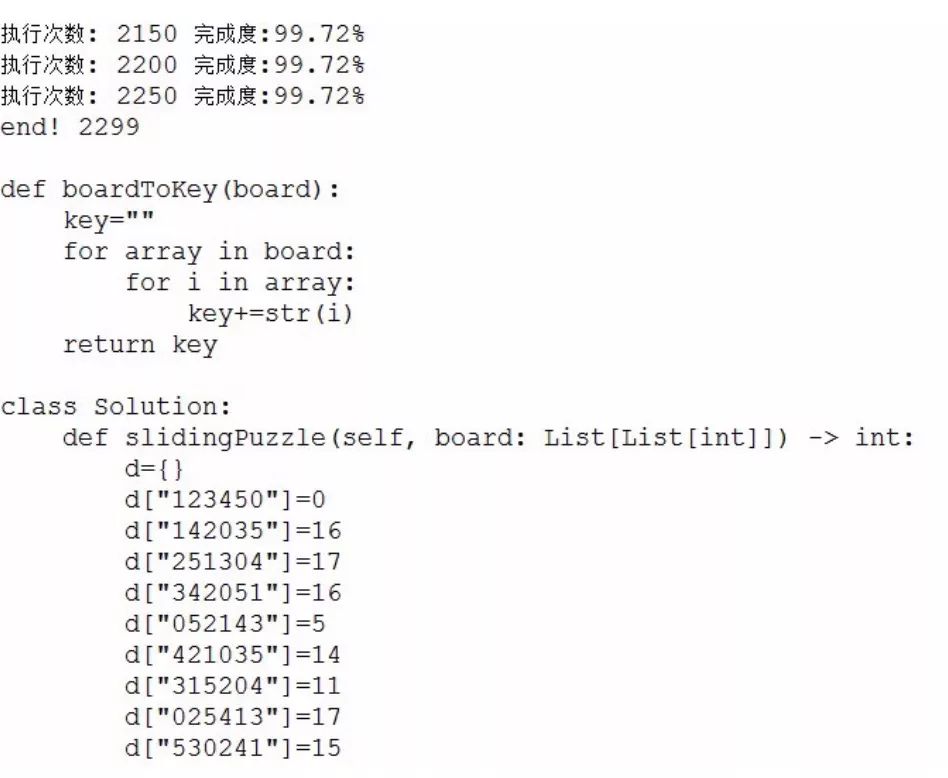
再看一下预测值的数据分布情况：

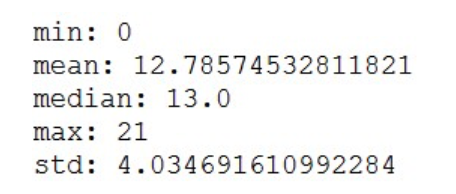
均值、最大值、方差比原来的佛系agent少了好几个数量级，均值和中位数几乎相等，经过这样的分析，我们心里至少有了一个底——模型是堪用的。

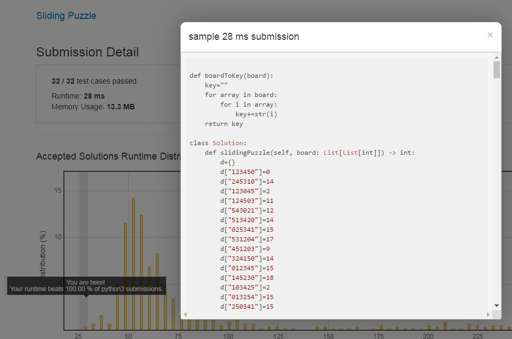
接下来便是见证奇迹的时刻，将控制台输出的代码copy到OJ系统进行提交(有兴趣的同学可以写个自动脚本)，看到如下结果：

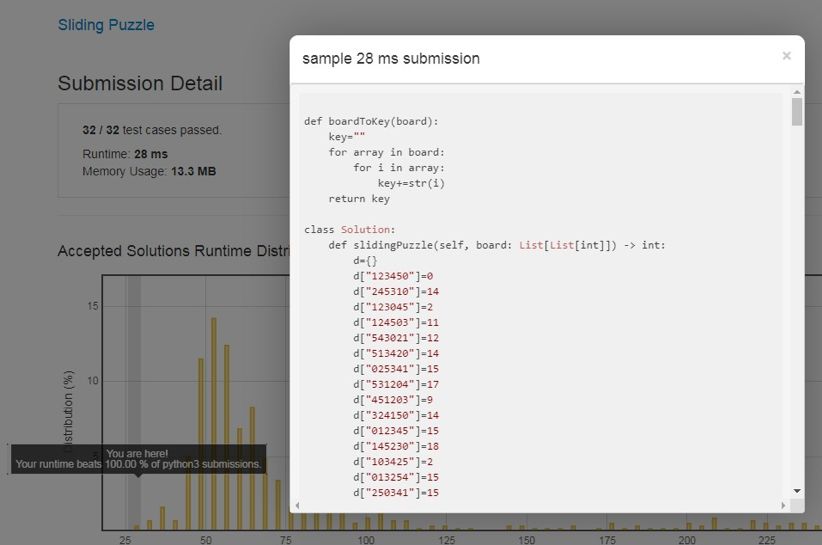
代码不仅AC了，还打败了100%的程序，并且成为了这一题的默认Solution！

好了，强化学习除了游戏、机器人、自动驾驶、NLP、CV等经典应用之外，一个新领域的潘多拉魔盒已经打开——刷题！

对比普通DQN以及经典解法

由于我们保存了平均奖励、平均步数，所以可以对比Rainbow模型和普通的DQN的训练效率。打开DrawLearningCurve.py这个文件并运行程序，观察到如下结果：

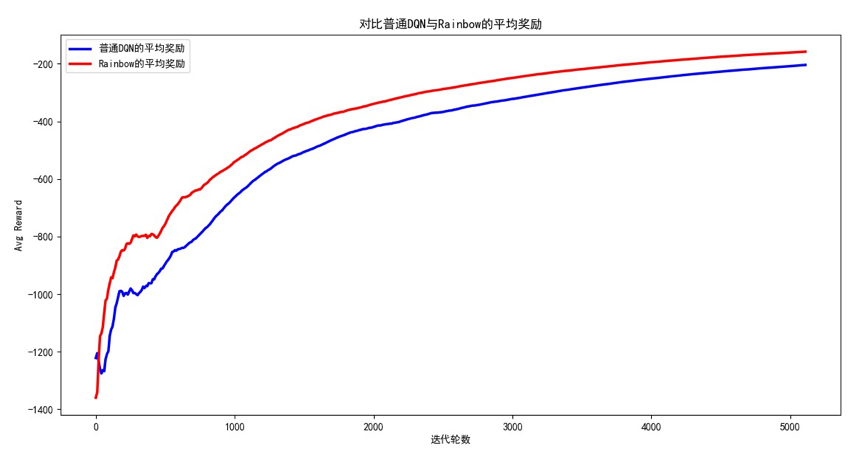
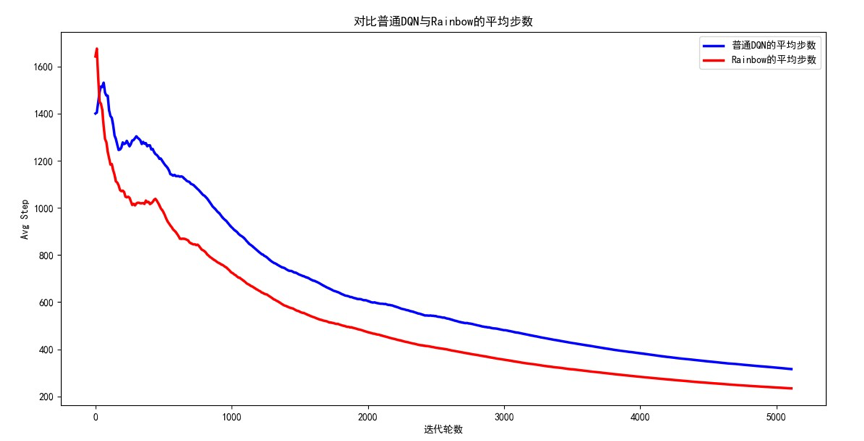
可以发现，无论是平均奖励还是平均步数，Rainbow一开始的表现并不比普通DQN好，但随着迭代次数的不断增加，Rainbow的平均奖励明显增加、平均步数明显减小，收敛速度也快于普通DQN。看来把DQN的各种改进算法整合到一起是有道理的，符合"集成学习器的效果往往优于单个学习器"的定律。如果进一步调参，学习曲线的差异会更加明显，读者可以自行尝试。

另外，和监督学习的测试方法类似，可以采用对拍的方式进一步测试强化学习算法，详见Duipai_Rainbow.py，它的主要步骤如下：

• 调用Permutation(全排列)生成输入数据(特征X)

• 调用StandardAStarSolve(标准A*算法)产生正确输出(标签Y_True)

• 调用TrainTest_Rainbow中的init_rainbow初始化rainbow模型，并进行预测(Y_Predict)

• 对比Y_True与Y_Predict，统计正确率Accuracy

还有一个小技巧，因为模型已经训练完毕，我们期待它的最优步数不会太大，所以设置一个阈值，如果某轮episode的步数超过这个阈值，就认为智能体进入了死循环，提前终止掉本轮episode：

#若步数超过阈值,则认为智能体进入了死循环step_threshold=256

运行main函数，可以看到如下输出：

未达到严格意义的100%，说明个别样本预测失败，模型并不是绝对的完美。这个现象很正常，因为参数化逼近的方式计算值函数，本身就是一种近似算法，一般来说都会存在误差。另外，强化学习毕竟加载了第三方库，所以比A*稍慢，这也是正常现象。

不到30毫秒的平均耗时，表明强化学习模型的预测速度是非常快的。所以：

只要OJ系统支持PaddlePaddle和PARL，就能使用强化学习算法切相当一部分Game题和Puzzle题，并且无需再打表！

以下表格展示了超参数对于结果的影响，读者可以试着调节超参数，看看哪些参数素会影响训练时间？哪些参数会影响平均奖励或平均步数的变化率？能否到达绝对的100%？

总结与展望

总结一下用强化学习算法切OJ题的主要步骤，可以画出如下流程图：

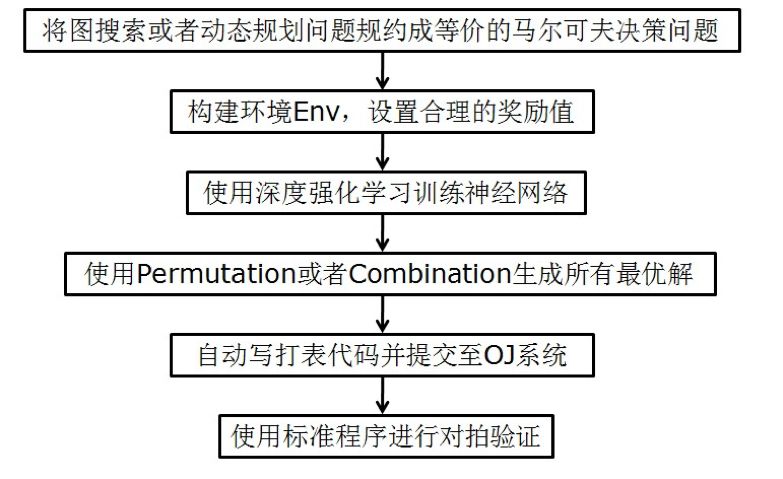
如果未来OJ系统支持PARL，那么就可以省去打表这一步，直接使用训练好的模型进行预测。

个人感想与注意点：

• RL与CLRS(算法导论)强关联，无论是动态规划，还是树搜索，或者OpenAI的线段树。

• 训练模型的时候，尽量在基线的基础上逐渐优化，比如buddaAgent、L2Cache、clipReward等参数和技巧都是实验出来的，不要一蹴而就的追求100%；这和做题思路是一样的，一般得到WA或者TLE之后，离AC也就不远了。

• 百度之星原题的起始状态和终止状态不固定，使用链表交点或者LCA即可解决，无需训练新的网络。

本文希望给大家两个启示：

• 是时候抛弃“刷题只是为了面试，其他地方用不到”的错误观念了！

• 强化学习能解决部分Game或者Puzzle类题目，并不适用于所有算法题；当然我期待大家能做出更强的AI，甚至是全自动读题、全自动写代码的AI。

百度AIStudio源码:  https://aistudio.baidu.com/aistudio/projectdetail/63441

强化学习PARL仓库：https://github.com/PaddlePaddle/PARL

本文提及的源码: https://github.com/kosoraYintai/PARL-Sample/tree/master/eight_puzzle

参考文献：

• Hado van Hasselt, Arthur Guez,Silver D.(2015). Deep Reinforcement Learning with Double Q-learning

• Tom Schaul, John Quan, Ioannis Antonoglou, Silver D.(2016). PRIORITIZED EXPERIENCE REPLAY

• Ziyu Wang, Tom Schaul, Matteo Hessel, et all.(2016). Dueling Network Architectures for DRL

• Matteo Hessel, Dan Horgan, Silver D, et all.(2017). Rainbow, Combining Improvements in DRL

• POJ 1077. Eight

• POJ 3264. Balanced Lineup

• LintCode 532. Reverse Pairs

• LeetCode 773. Sliding Puzzle

• LeetCode 307. Range Sum Query - Mutable

• LeetCode 47. Permutations II

●编号864，输入编号直达本文

●输入m获取文章目录