在上一小节里,我们提出了线性方程组无解和直线拟合这两个实际的问题,并最终指出了问题的解决方向,即:在问题的精确解不存在的情况下,我们可以通过求取距离目标最近的近似解来最大限度的解决问题,并且定义了在这个问题背景下最近距离的有关概念,告诉了读者如何利用矩阵投影的方法来寻找任意点到指定子空间的投影以及最近距离。这其实也是实际工程中比较常用的解决方法和思考途径。
在这一小节里,我们会继续运用这一思想方法,深入的剖析最小二乘法这个解决近似问题的有力武器,基于矩阵四个子空间所具有的正交、互补的优良性质,在投影问题通用公式的基础上,最终实际解决方程近似解的求解以及空间多点直线拟合的问题。
我们知道,在一个 空间中有一个向量b,我们可以选取m个线性无关的向量
空间中有一个向量b,我们可以选取m个线性无关的向量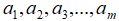 作为
作为 空间中的一组基,我们将向量b向每个基向量上进行投影,就能够得到m个投影向量:
空间中的一组基,我们将向量b向每个基向量上进行投影,就能够得到m个投影向量: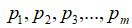 ,并且显而易见的是,他们满足:
,并且显而易见的是,他们满足: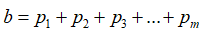 ,即通过空间中所有投影轴上的投影向量能够重构出向量b的完整信息。
,即通过空间中所有投影轴上的投影向量能够重构出向量b的完整信息。
从这个浅显的结论中我们能得到什么呢?我们举一个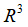 空间的例子来仔细看看,我们选取其中三个线性无关的向量
空间的例子来仔细看看,我们选取其中三个线性无关的向量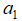 ,
,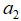 ,
,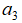 ,由他们构成一组基,向量b在各个基向量上的投影分别为
,由他们构成一组基,向量b在各个基向量上的投影分别为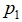 ,
,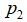 ,
,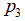 ,这个自然不用多说。如果此时我们把向量
,这个自然不用多说。如果此时我们把向量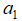 和向量
和向量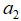 看作是一个二维子空间中的基向量,那么向量b向这个平面上的投影就可以表示为往向量
看作是一个二维子空间中的基向量,那么向量b向这个平面上的投影就可以表示为往向量 和向量
和向量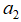 上的投影向量之和:
上的投影向量之和: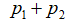 ,此时向量
,此时向量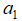 和向量
和向量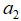 所张成平面上的投影联合向量
所张成平面上的投影联合向量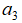 上的投影一道,同样能构建出整个b向量。
上的投影一道,同样能构建出整个b向量。
因此,在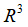 空间中,基向量
空间中,基向量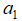 和
和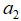 张成的二维子空间和由向量
张成的二维子空间和由向量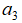 构成的一维子空间之间是互补的关系。概况的说,互补的子空间一方面由不同的基向量所张成,另一方面他们的维数之和为整个
构成的一维子空间之间是互补的关系。概况的说,互补的子空间一方面由不同的基向量所张成,另一方面他们的维数之和为整个 空间的维数。空间中的任意一个向量b,其在互补子空间上的投影向量之和,就是向量自身。
空间的维数。空间中的任意一个向量b,其在互补子空间上的投影向量之和,就是向量自身。
我们这里直接拿出定义:子空间V和子空间W满足正交关系成立的条件是:子空间V中任意一个向量v和子空间W中任意一个向量w都垂直。
为了更明确的说清这个概念,这里我们看看图1。
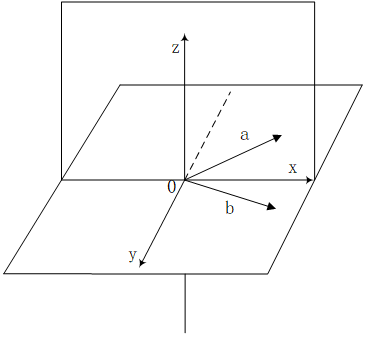
图1 寻找图中的正交子空间
其实从视觉直观上我们会觉得,xoz和xoy这两个子空间是相互垂直的,但是实际上并不是,我们对照定义检查一下,这两个子空间中的任意向量两两之间并不一定满足垂直关系,例如向量a和向量b,这两个向量就不垂直。
其实最明显的一个矛盾之处在于:位于x轴正方向上的向量同时存在于这两个子空间中,那么依据定义他应该与自己垂直,但是这显然是不可能的。因此,我们从这个例子中可以得到一个结论,同时位于相互正交的两个子空间上的向量只可能是零向量,因为只有零向量才和自身保持垂直。
那么从上面的分析中可以得知,在图1中,和子空间xoy正交的子空间只能是z轴这个一维子空间了。
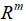 空间中的两个互补的子空间,如果满足相互正交的关系,则他们满足正交补的关系,他们的空间维数之和应该为m。在图1中,z轴和xoy子空间就是满足正交补关系的两个子空间,但是像x轴和z轴,他们仅仅是正交,但并不满足互补的关系。
空间中的两个互补的子空间,如果满足相互正交的关系,则他们满足正交补的关系,他们的空间维数之和应该为m。在图1中,z轴和xoy子空间就是满足正交补关系的两个子空间,但是像x轴和z轴,他们仅仅是正交,但并不满足互补的关系。
你可能在想,这前前后后说了这么多的概念,我们到底想要干什么呢?回顾一下,上一节中,我们在一个子空间中寻找与目标向量b距离最近的投影向量p,前提就是误差向量 与投影向量p相互垂直。由于
与投影向量p相互垂直。由于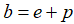 且满足
且满足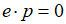 ,则向量p所在的子空间和向量e
所在的子空间在
,则向量p所在的子空间和向量e
所在的子空间在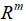 中就构成了正交补的关系。
中就构成了正交补的关系。
那么,我们去哪里寻找这样的正交补子空间呢?我们从矩阵的四个子空间入手,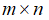 规模的矩阵A,首先所有满足Ax=0等式成立的向量x构成了矩阵A的零空间N(A)。对于这个式子,我们展开来看就是:
规模的矩阵A,首先所有满足Ax=0等式成立的向量x构成了矩阵A的零空间N(A)。对于这个式子,我们展开来看就是: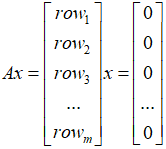 ,即满足任意的
,即满足任意的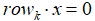 成立,这表明任意一个行向量与任意一个零向量垂直,因此行空间和零空间是正交子空间。同时,我们在前面讲过,这两个子空间的维数之和为n,因此矩阵A的行空间和零空间在
成立,这表明任意一个行向量与任意一个零向量垂直,因此行空间和零空间是正交子空间。同时,我们在前面讲过,这两个子空间的维数之和为n,因此矩阵A的行空间和零空间在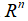 空间中满足正交补的关系。
空间中满足正交补的关系。
我们直接利用上面的结论可以知道:转置矩阵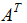 的行空间和零空间当然也是相互正交的,因此,矩阵 A的列空间和左零空间在
的行空间和零空间当然也是相互正交的,因此,矩阵 A的列空间和左零空间在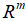 中同样满足正交补的关系。
中同样满足正交补的关系。
通过上面的思考过程,我们找到了这两组满足正交补关系的子空间,那我们是不是就知道了应该向哪儿投影了呢?对,没错。
我们沿着上文讨论的思路,首先处理无解方程组的近似解问题。我们回顾一下本章最开始的这个方程组: 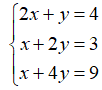 ,我们把方程组写成矩阵相乘的形式:
,我们把方程组写成矩阵相乘的形式: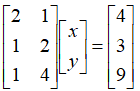 ,其中,我们令矩阵
,其中,我们令矩阵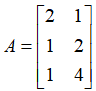 ,向量
,向量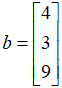 。
。
我们知道矩阵A的列向量的线性组合构成了他的列空间,如果要求方程组有解,则必须满足向量b在矩阵A的列空间上。很遗憾,此时向量b并不在矩阵A的列空间上,因而方程组无解。
那么,我们就应该在矩阵A的列空间上寻找一个距离向量b最近的向量,用它来表示方程组的近似解。因此,线性方程组近似解的问题就被我们转化为了熟悉的“向量向二维子空间投影的问题”了。转化后的等价问题描述如下:
我们将向量b向矩阵A的列空间进行投影,获得投影向量p。而误差向量e则正是向量b向列空间的正交补子空间------左零空间上的投影。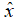 向量则是我们最终想要获取的近似解向量:
向量则是我们最终想要获取的近似解向量: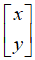 。
。
因此,我们直接套用3.1节中的公式:
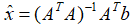 ,我们代入具体的数值,就能得到线性方程组的近似解向量:
,我们代入具体的数值,就能得到线性方程组的近似解向量: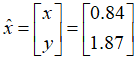
即这个方程组的近似解是: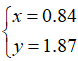 。
。
我们从最终结果出发再讨论一下近似的概念,我们把近似解带回到原方程中,就得到了一个三维列向量: ,我们称x=0.84,y=1.87为线性方程组的近似解,正是因为由此得到的三维向量
,我们称x=0.84,y=1.87为线性方程组的近似解,正是因为由此得到的三维向量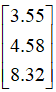 是列空间中距离原向量
是列空间中距离原向量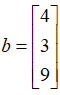 距离最近的一个向量。
距离最近的一个向量。
我们这里用Python工具来检验一下计算结果:
代码如下:
import numpy as np
from scipy import linalg
A = np.array([[2, 1],
[1, 2],
[1, 4]])
b = np.array([[4],
[3],
[9]])
A_T_A = np.dot(A.T,A)
x = np.dot(np.dot(linalg.inv(A_T_A),A.T),b)
print(x)
运行结果:
[[ 0.83870968]
[ 1.87096774]]
这里得到的结果和我们文中的分析结果一致。在这个过程中涉及到了矩阵转置、矩阵乘法、矩阵求逆等基本运算,这些在之前的各个章节里都详细讲解过,在这里我们进行的是一个综合应用。
补充说明一点,n维空间中的向量x和向量y的距离,我们定义为:
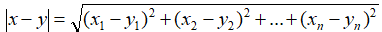 。
。上面用来求取无解线性方程组近似解的方法就是最小二乘法,这个名字既熟悉又有些拗口,最小二乘这几个字到底是什么意思?我们再用这个方法去解决第二个问题,随后大家就会更清楚一些。
我们在平面上选取三个点:(0,1),(1,4),(2,3),找一条最接近这三个点的直线。我们设直线的方程是:y=cx+d,代入这三个点的坐标看看:
显然,通过观察发现:变量c和d是无解的,那么还是老套路,我们令矩阵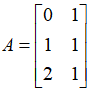 ,向量
,向量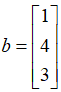 ,将方程组转化为
,将方程组转化为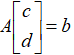 的矩阵乘法形式。我们直接套公式去求取结果:
的矩阵乘法形式。我们直接套公式去求取结果: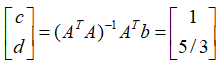
通过求取变量c和d的近似解,我们得到了最接近(0,1),(1,4),(2,3)这三个点(也就是拟合了这三个点)的直线解析式: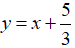 ,我们来看看拟合后的直线与拟合点之间的关系,如图2所示。
,我们来看看拟合后的直线与拟合点之间的关系,如图2所示。
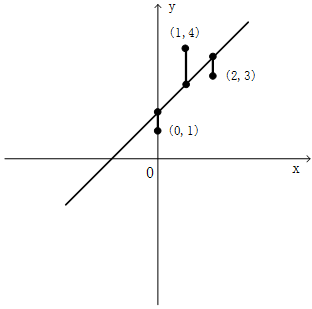
图2 最小二乘线性拟合
从图中可以看出,我们用一条直线拟合了这三个不在一条直线上的点。到这里,我们的思考过程其实并没有结束,还有一个重要的地方相信大家也都发现了,即,在图中每一个点都向直线引了一条竖直的直线,这又是干什么用的?
我们还是回到“最近”的定义上来讨论,“最近”指的是投影向量p与向量b的距离最近。而在这里,向量p实际上代表了什么含义呢?我们依照定义来看,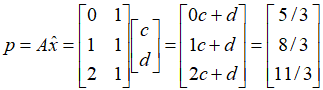 ,向量p的三个成分指的是什么?
,向量p的三个成分指的是什么?
其实这个问题的答案不难想到,向量p的三个成分实质上就是对应横坐标分别为0,1,2时,位于直线上的三个点的纵坐标,而对于向量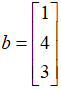 ,他的三个成分则分别就是三个待拟合的原始点的纵坐标。
,他的三个成分则分别就是三个待拟合的原始点的纵坐标。
此时,最小二乘法的目标就是使得误差向量e的模长最小,这个最优化的目标就被表示为: ,在图上所代表的几何意义就是使得三段竖直线长度的平方和开根号后取到最小。
,在图上所代表的几何意义就是使得三段竖直线长度的平方和开根号后取到最小。
我们最后来回顾一下两个要点:
1、绘制一条距离三个点最近的直线,判定的指标是三个点到直线的竖直线,而不是直观上最容易想到的垂直线。
2、为什么叫最小二乘,这个方法从字面上理解是什么意思?最小二乘就是最小平方的意思,我们的优化目标就是去求解三条竖直线长度的平方和开根号后的最小值,相信这么一说,读者应该就十分清楚了。