作者 | Mr Bear
前不久,帝国理工学院教授、Twitter 首席科学家 Michael Bronstein 发表了一篇长达160页的论文,试图从对称性和不变性的视角从几何上统一CNNs、GNNs、LSTMs、Transformers等典型架构,构建深度学习的“爱尔兰根纲领”。
AI科技评论曾报道过对Michael Bronstein论文的精彩介绍,本文内容是他通过视频演讲的方式对几何深度学习进行的更深度分析。
视频链接:https://www.youtube.com/watch?v=8IwJtFNXr1U
以下是报告原文,AI科技评论进行了不改变原意的整理。

首先,Michael Bronstein 教授介绍了「几何深度学习」的定义。就「深度学习」而言,这一强大的技术已经家喻户晓,它深刻改变着现代工业和我们生活的方方面面。在这里,我们着重讨论「几何深度学习」中有关「几何」的部分。
回顾历史,大约从公元前 300 年开始的 2,000 多年间,我们谈到「几何」几乎就等同于「欧氏几何」,几乎没有其它类型的「几何」学说被广泛地使用。
图 3:非欧几何的兴起
到了 19 世纪,这种欧氏几何的垄断被打破了。彼时,罗巴切夫斯基、高斯、波尔约、黎曼等数学家首次给出了非欧几何的例子,「射影几何」、「仿射几何」等一系列创新的几何学说也随之兴起。19 世纪末,这些学说分化为了一些完全不同的研究领域,数学家们开始讨论哪些几何学说真实成立,我们究竟该如何定义「几何」,以及是否存在大一统的几何学原理能将各种几何学说统一起来。
图 4:克莱因与爱尔兰根纲领
年轻的德国数学家克莱因于 1872 年成为了爱尔兰根大学的教授,他指出了解决这一问题的方法。1872 年,克莱因在爱尔兰根大学发表了流传于世的题为「关于近代几何学研究的比较评述」的演讲,该演讲也被后人称为「爱尔兰根纲领」。在这次演讲中,克莱因从不变性和对称性的角度研究几何,在进行某些变换的条件下,这些性质会保持不变。
图 5:通过群论定义几何
这种方法通过适当选择的对称性变换来定义不同的几何类别,并且通过群论的语言对其进行形式化定义(注:「群论」这一数学学科也诞生于 19 世纪)。到了 1920 年,Elie Cartan 透过这种不变性和对称性的视角将各种几何学统一了起来。
爱尔兰根纲领对几何学和数学的影响是十分广泛且甚远的,其影响也延伸到了其它的领域。尤其是,在物理学领域中,通过考虑对称性可以根据热力学第一定律推导出守恒定律,这就是著名的「Noether 定理」。
图 6:规范不变性与力学的统一
直到几十年之后,杨振宁和 Mills 在 1954 年提出规范不变性的概念,证明这一基本原理成功地统一了自然界所有基本的力(重力例外),这就是所谓的标准模型。他们描述了我们目前所知的所有物理现象。用诺贝尔奖获得者、物理学家 Philip Anderson 的说:稍显夸张地说,物理学就是对对称性的研究。在计算机科学领域,爱尔兰根纲领也有着巨大的影响。例如,我们可以将「范畴学」看做爱尔兰根纲领的延伸。
深度学习的「爱尔兰根纲领」
那么,几何学的发展与深度学习有何关系呢?实际上,深度学习领域目前的研究情况与 19 世纪几何学的发展十分类似。
图 7:几何深度学习
一方面,在过去的十年间,深度学习为数据科学带来了一场真正的革命,让许多以前被认为无法完成的任务成为了可能,无论是在计算机视觉、语音识别,还是像围棋这样的智能游戏任务。
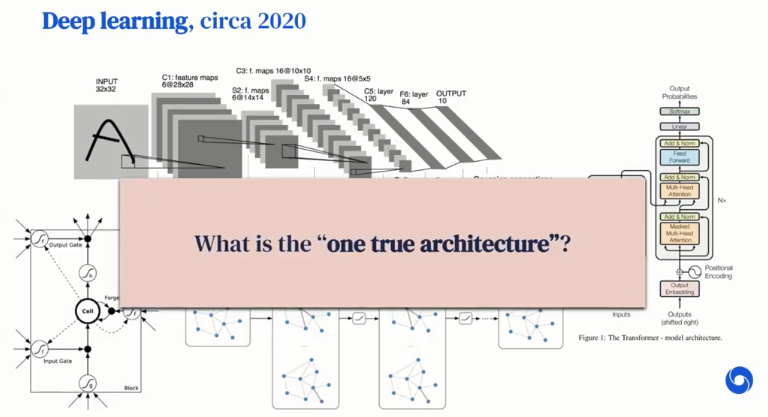 图 8:现代深度学习系统
图 8:现代深度学习系统
另一方面,我们已经建立起了各种各样的用于不同类型数据的神经网络架构(例如,卷积神经网络、图神经网络、Transformer、LSTM 等),这些系统是图灵完备的。然而,我们至今仍然缺乏统一的深度神经网络架构设计原理。因此,我们很难理解不同模式之间的关系,也不可避免地导致对相同的概念进行重复发明和重复命名。
本着与「爱尔兰根纲领」统一几何学相类似的精神,我们需要对深度学习进行相似的统一,Michael Bronstein 教授等人将其称之为「几何深度学习」。这样做有两个目的:首先,我们将提供一个通用的数学框架来推导出最成功的神经网络架构;第二,我们将给出一个建设性的过程通过某种原理来创造新的深度学习架构。2015 年,研究者们提出了「几何深度学习」,随后这一术语流行了起来。目前,人们几乎只在图神经网络领域使用几何深度学习。实际上,几何深度学习可以在更加广阔、更加有趣的场景下被使用。
图 9:机器学习黑盒
简而言之,机器学习本质上是一个函数估计问题。给定训练集上某个未知函数的输出(例如,带标签的狗和猫的图像),机器学习算法试图从一些假设类中找到一个函数,它可以很好地拟合训练数据,使我们可以预测给定的输入的输出。
过去的数十年间,以 ImageNet 为代表的大型高质量数据集涌现了出来,同时我们也拥有了大量的 GPU 计算资源,使我们可以设计各种各样的函数,可以在大型数据集上进行操作。
图 10:最简单的神经网络
即使我们使用如图 10 所示的最简单神经网络架构,我们可以生成一个全连接的两层分类网络,这使我们可以以很高的准确率近似任意的连续函数,即「万能近似定理」。
图 11:万能近似定理
在低维度下,上述情况是近似理论中的一个经典问题。研究人员对此研究得非常透彻,从数学上说,我们对估计误差可以实现非常精确的控制。然而,到了高维情况下,情况则完全不同。如图 12 所示,即使为了近似一个简单的连续函数类(在单位正方形内切圆的四分之一圆处嵌入一个高斯函数),样本的数量会随着维度的上升而呈指数级增长。这一现象被称为「维度诅咒」。
图 12:维数诅咒
由于现代机器学习算法需要处理具有数以千记、甚至数以百万计的维度的数据,我们会经常遇到「维数诅咒」的困扰,即使我们将目标函数限定为最简单的(1-李普希兹)函数,学习过程也无法进行下去。
图 13:低维映射也无法完全解决维数诅咒
一些研究人员试图通过低维映射解决维数诅咒问题。然而,除非数据的流形可以被很好地映射到超平面上,否则这种低维映射学习的效果十分有限。例如,浅层多层感知机中的线性层将在很大程度上丢失输入数据真实性。
这一现象可能在计算机视觉领域最为突出。如图 14 所示的图像分类例子中,即使是微小的图像也具有很高的维度。直观地说,当我们把图像解析成一个向量并将其输入给简单的感知器神经网络时,有很多图像中的结构被破坏和丢弃。假如图像仅仅被移动一个像素,由输入得到的向量也会变得十分不同。因此,我们需要使用大量的样本来训练神经网络,从而使其学习到这些被移动后的图像也应该被分到同样的类别中。
图 14:图像中被破坏和丢弃的结构
Hubel 和 Wiesel 于 1962 年在神经科学领域的经典工作为上述计算机视觉问题给出了解决方案。他们对视觉皮层的研究说明了脑神经元会组织成局部感受野,该工作也获得了 1981 年的诺贝尔医学与生理学奖。该工作为一类具有局部共享权值的新型神经网络架构提供了设计了灵感。1980 年,福岛邦彦首次提出了新认知机(neocognitron);接着,Yann LeCun 发明了卷积神经网络,通过在图像间共享权重解决了维数诅咒的问题。
图 15:卷积神经网络中的权值共享
图 16 展示了咖啡因的分子结构,该结构可以被表征为一个图。在该图中,节点代表原子,而边代表化学键。如果我们想要将神经网络应用于这种输入,从而预测某些化学性质(例如,某些受体的键能),我们也可以将其表征为一种向量。然而,此时我们无法处理图中节点的排列方式,因为在图像中,我们并没有考虑节点的优先顺序。
图 16:咖啡因分子结构
实际上,分子结构只是具有不规则的非欧结构的数据中的一种,我们希望将深度学习技术应用于该领域。此外,社交网络也是另一个非常重要的使用非欧结构数据的场景。社交网络中万网包含数以亿计的节点。生命科学领域中的交互网络也符合非欧的结构特征。计算机图形学中的网格数据也属于这一范畴。我们需要通过某种准则来处理上述存在非欧结构的数据。
图 17:各种具有非欧结构的网络数据
因此,面对如图 12 中所示的看似难以解决的多维度图像分类任务,我们可以考虑利用来自输入数据的几何结构的额外结构信息。我们将这种结构称作「几何先验」,这是一种强大的通用原理,为解决维数诅咒问题带来了希望。我们可以通过一些归纳偏置来引入一些关于几何性质的假设,这样可以有效地根据几何性质对假设空间中的函数进行限制,使高维问题可以更好地得到解决。举例而言,我们通常会希望对图像数据的分类结果与平移操作无关,对球形空间中数据的计算结果与旋转操作无关,而对图数据的处理结果与图同构性无关。
图 18:引入几何性质
图 19:关键概念
假设数据存在于域 Ω(集合)中,对于图像而言,Ω 中的元素 u 为限速,而图数据中的元素则为节点。我们假设域中的一些元素构成了一个特征空间 C(例如,每个像素的 RGB 值或者图中节点的特征),其中 C 的维度被称为通道。我们可以通过特征函数 X(Ω,C) 的空间来定义带有特征的域,该函数的输入为域 Ω 中的数据,其输出为特征空间中的特征 C(即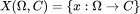 )。实际上,在离散的环境中,我们可以将 X 看做一个特征矩阵。该函数空间具有向量空间结构,具体而言,它满足分配律的性质,即:
)。实际上,在离散的环境中,我们可以将 X 看做一个特征矩阵。该函数空间具有向量空间结构,具体而言,它满足分配律的性质,即:
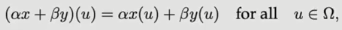
给定特征空间 C 上的内积
,以及域 Ω 上的测度 μ,我们可以将函数空间 X(Ω,C) 上的内积定义为:
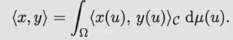
原理 1:对称群
对称是一种保持底层物体性质不变的变换,因此它需要具备结合性、可逆性,需要包含单位元。事实上,我们可以通过群的概念对对称进行推理,群中的元素为对域的变换。群需要满足结合律、具备封闭性,群存在单位元,群中每个元素存在逆元。
图 20:对称群
群操作
图 21:群操作
群操作指的是将群中的元素 g 作用于域中的元素 u(例如,对图像进行平移、旋转,或对集合中的元素进行排列)。我们重点关注具有线性性质的群操作,这是我们可以使用线性代数的方式来表示群操作。
图 22:不变性和等变性
我们可以通过利用群 G 中的对称性在很大程度上简化机器学习中的高维问题。从全局的角度看,当我们对输入施加群操作并不影响输出的结果时,则函数 f 对于 G 中的操作具有不变性(例如,图像分类);从局部的角度看,当对输入施加的影响也会同时时输出发生相同的变化时,则函数 f 对于 G 中的操作具有等变性(例如,图像分割)。
在图像分类的例子中,输入并不只是一个 d 维向量,它还是在某个域上定义的信号。在如图 23 所示的例子中,这里的信号是一种二维网格。我们通过对称群来捕获该域的结构。在本例中,群中的操作为作用在域中点上的二维平移。在信号空间中,群在域上的操作体现为群表征。在本例中,该操作为简单的平移操作,或在 d 维向量上运算的 d*d 矩阵。
图 23:几何先验
这种输入信号之下的域的几何结构将结构信息施加于待学习的函数 f 上。我们可以找到一些不受群中操作影响的函数,并将其称为「不变函数」。例如,在图像分类任务中,无论猫的位置在图中的何处,我们都希望模型将该图像分类为「猫」。这种性质被称为平移不变性。
另一方面,在某种情况下,函数具有相同的输入和输出结构。例如,在图像分割任务中,输出是像素级别的标签掩模,因此输出也是一种图像。在本例中,我们希望输出可以与输入通过相同的方式变换,这是一种被称为「平移等变性」的等变函数。
原理 2:尺度分离
现实世界中的数据往往充满噪声,输入数据所经受的所有操作不一定对于真实值是对称的。如下图所示,图中的房子可能会发生扭曲,但是我们仍然需要识别出这是一个房子,我们希望输入信号对于域的轻微变化是稳定的。因此,我们试图通过将局部操作进行组合来对大规模交互建模。这是因为局部的操作往往并不会在全局上传播误差,使用局部细节也有助于支撑网络层的局部性。这种情况与信号处理领域中傅里叶变换和小波变换的区别相类似。
图 24:尺度分离
几何深度学习的基本模块
图 25:几何深度学习的基本模块
首先,我们需要设计一种等变性层,它们对域中元素的变换与群操作保持一致,并且具有局部性。如果我们希望得到对于整个域的全局预测结果,我们则需要设计类似于卷积神经网络中全局池化层这样的不变性层。
我们之所以只需要重点考虑线性的群操作,这不仅是因为我们可以从群操作的视角考虑所有的深度学习问题,还因为我们可以通过 ReLU、Tanh 这样的激活函数为每一个点加入非线性。根据万能近似定理,我们就可以使用线性操作和激活函数表示大多数的非线性函数。
此外,在某些应用中,局部池化(或下采样)操作是非常有效的。尤其是当域非常大时,我们通过池化操作缩小初始的域,并且保持域中最重要的部分。
图 26:几何深度学习设计准则
上述两个原理为我们给出了一种通用的几何深度学习的设计准则,可以通过之前的深度学习架构完成识别任务。我们可以使用一系列的等变性层(例如,CNN 中的卷积层),然后使用一个具有不变性的全局池化层将所有的信息聚合到单个输出中。在某些情况下,我们还可以通过局部池化构建层次化的域。
图 27:流行深度学习架构的推导方法
几何深度学习的「5G」
我们可以将上述通用的设计方式应用到不同的几何结构上,例如:网格(Grids)、具有全局变换群(Groups)的同构面、图(Graphs)、集合、以及具有全局等距方差和局部测量(Geodesics & Gauges)对称性的流形上。Michael Brostein 等人将这些情况称为几何深度学习的「5G」。
图 28:几何深度学习的「5G」
在上述原理的指导下,人们设计出了目前深度学习中最流行的一些架构,例如:基于平移对称性的卷积网络、基于置换不变性的图神经网络和 Transformer、根据规范对称性推导出的用于图形学的 Intrinsic CNN。
图 29:深度学习架构一览
图数据上的几何深度学习
对于图数据而言,上述深度学习方法非常实用,可以解决一些巨大的科学问题,包括理解蛋白质的生化性质、药物发现,以及错误信息检测。
首先,我们将介绍「图」的概念。以社交网络为例,这种图可以对用户之间的关系和交互进行建模。从数学上来说,社交网络中的用户可以被建模为图中的节点。节点对之间的关系可能是有序的(有向图),也可能是无序的(无向图)。图中的节点可能也带有附属的特征,我们可以用一个 d 维向量对这些特征进行建模。
图 30:图结构数据
图具有一个关键的结构特征,即我们没有一套规范的方法来排列这些节点。如图 21 所示,当我们在表征图结构的邻接矩阵中组织这些节点时,我们会自动地为节点指定任意的顺序。如果我们通过不同的方式为节点编号,那么特征矩阵的行和对应的邻接矩阵的行和列都会根据某种置换(改变点的顺序)矩阵 P 来排列,此处的 P 代表了置换群,该置换群中有 n 的阶乘个元素。从线性代数的角度出发,我们可以将每个置换操作表示为一个 n*n 的矩阵(群操作)。
图 31:节点排序与置换群
如果我们希望以整张图作为输入,并得到单个输出的值(例如,预测分子图中某个键的键能),我们需要保证输出不会受到输入节点排序的影响。我们将这种性质称为「置换不变性」。
图 32:置换不变性
另一方面,我们有时也希望进行一些节点级别的预测(例如,社交网络中的恶意用户检测)。此时,我们希望函数能够随着节点的重新排列而变化。换而言之,我们希望函数具有「置换等变性」。
我们可以使用节点的局部邻域来构建各种易于处理的函数。对于通过边连接起来的各个节点你,我们可以将其特征向量聚合起来,从而得到某种局部表征。由于我们并没有对邻居节点进行排序的规则,所以这一聚合过程也应该具有置换不变性,我们将该聚合函数记为 φ。
图 33:具有置换不变性的聚合函数
当我们将聚合函数 φ 应用于图中的节点并将聚合的结果堆叠在一个特征矩阵中时,我们将得到具有置换等变性的函数 F。显然,构建局部函数 φ 的方式是十分重要的,对 φ 的选择会决定最终得到的架构的表达能力。
图 34:φ 的置换等变性
当 φ 为单射时,我们可以证明:通过上述方式设计的图神经网络等价于 Weisfeiler-Lehman(WL)图同构测试。这是一种非常经典的图论算法,它试图判断几张图是否同构,该过程是一个迭代式的标签优化过程。
如图 35 所示,局部的聚合函数(如求和、取平均、取最大值)应该具有置换不变性,可学习的函数 ψ 对邻域特征进行变换,另一个可学习函数 则使用从邻域中聚合的信息来更新节点 i 的特征。非线性函数 ψ 的输出同时取决于节点 i 和节点 j,其输出可以被看做从节点 i 到节点 j 的消息,我们用它来更新节点 i 的特征。
图 35:消息传递机制
这种图神经网络被称为消息传递网络。2017 年,任职于 DeepMind 的 Justin Gilmer 将其引入了化学领域的应用中。而我们也在论文中将其应用于计算机图形学。
图 36:从几何深度学习角度看图神经网络
通过观察一些典型的 GNN 架构,你会发现前文提到的几何深度学习设计准则也同样适用。在这里,我们将置换群作为几何先验。通常而言,我们会先使用一系列具有置换等变性的层(消息传播层或融合层),接着我们可以选用全局池化层生成单一的图级别的读出结果。在某些框架中,我们有时也会使用通过图粗化操作实现的可学习的局部池化层。
图 37:DeepSets
对于图神经网络而言,在某些特殊情况下会发生非常有趣的现象。首先,没有变的图可以被看做一个集合,这个集合是无序的。此时,最直接的方式是通过对特征向量使用函数,完全独立地处理集合中的每一个元素。这种在集合上定义的函数是具有置换不变性的,它是图神经网络的一种特例。我们将这种架构称为「DeepSets」。
图 38:Transformer
在另一种极端情况下,我们假设元素之间两两交互,从而构成了一个完全图。在这里,我们可以使用一种基于注意力的聚合函数,我们可以将其看作一种可学习的 soft 邻接矩阵,这便是如今在自然语言处理和图学习领域非常流行的 Transformer 架构。Transformer 通常被用于分析文本序列,其中节点的顺序已经被位置编码给定。位置编码是一种额外施加给节点的唯一的特征。
图 39:图子结构网络
对于一般的图而言,也存在类似的处理过程。我们可以使用多种方式对节点的位置进行编码。在 Michael Brostein 及其学生近期发表的一篇论文中,他们对图中的一些小型结构(例如,三角形或团)计数,通过这种方式得到了结构编码,这种编码可以使消息传递算法适用于不同的邻域。他们将这种算法称为「图子结构网络」,在选择恰当的子结构的情况下,该网络的性能要严格优于 WL 测试。通过对子结构进行技术,我们还可以引入针对特定问题的归纳偏置。例如,在分子结构图中,环是最突出的结构之一,有大量的化合物(如咖啡因)包含芳香环。
图 40:归纳偏置——包含环的化合物
实验结果表明,通过使用该网络架构,如果我们对五元环或六元环进行计数并将其输入给结构编码,可以显著提升我们预测分子性质的能力。
潜图学习
图 41:将计算图从输入图中解耦
当我们需要计算的图并不是给定的输入图时,仍然可以通过图神经网络进行处理。实际上,近年来有许多研究工作试图通过将计算图从给定的输入图中解耦出来,从而进行消息传递。这类方法包括通过图采样解决概率化的问题、重新构图,或使用更大的多跳图滤波器(从邻居的邻居聚合信息)。
图 42:潜图学习
我们还可以学习出计算图,进而在该图上运行图神经网络,并为下游任务优化该网络。我们将该这种学习问题命名为「潜图学习」。我们可以使这种计算图的构造过程可微,并且对其应用反向传播。我们也可以在网络的不同层之间更新该图,这就是所谓的「动态图卷积神经网络」,它同时也是首个实现潜图学习的架构。
图 43:流形学习
也许从历史的角度来说,潜图学习与流形学习(或称非线性降维)。流形学习技术曾经是一种用于数据可视化的常用技术。流形学习的关键假设是:尽管数据存在于高维空间中,但是数据都具有内在的低维结构,「Swiss roll」曲面就是一个很好的例子。假设我们的数据点都是从某些流形上采样得来,而我们可以通过一个局部的图捕获这些流形的结构,从而将其嵌入到一个低维的空间中。通常而言,在这个低维空间中应用机器学习技术更为方便。然而,流形学习之所以并没有在数据可视化之外的领域大放异彩,是因为图 33 中的三个步骤相互独立。显然,第一步中构图的结果对下游任务影响很大。我们常常需要在算法的不同阶段进行手动的调优,从而使其能够具有好的效果。
图 44:潜图学习
通过潜图学习,我们可以为这些算法带来新生,因此 Michael Brostein 将其称为「流形学习 2.0」。我们可以构建一个端到端的工作流程,同时在图神经网络中构建计算图和图上的滤波操作。近期,Michael Brostein 提出了一种名为「可微图模块」 (DGM)的潜图学习架构,并将该架构用于自动疾病诊断应用程序,其性能一致由于使用人造特征的图神经网络。
网格
图 45:环图
接下来,我们将从另一个视角讨论另一种几何结构——网格。网格是一类经常被研究的图,图 45 展示了一种被称为「环图」的网格。
与一般的图相比,我们首先应该注意到网格拥有一种固定的邻域结构,这不仅仅体现在网格中邻居节点的顺序是固定的。在一般的图中,由于邻居节点并没有一种标准的顺序,所以我们不得不使用一具有置换不变性的局部聚合函数 φ。然而,在网格中,我们有这种标准的邻居节点顺序。如图 45 所示,我们在序列中总是可以使绿色节点在红色节点之前,且红色节点在蓝色节点之前。如果我们选择使用线性函数进行一些聚合运算,就可以完成卷积操作。
图 46:线性局部聚合函数
如果我们使用矩阵表示上述情况,就会得到一种特殊的结构——循环矩阵。我们通过移位某个参数向量的副本生成循环矩阵,这也正是卷积神经网络中的「权值共享」的概念。
图 47:循环矩阵=卷积
循环矩阵是一种特殊的矩阵,它满足交换律。不仅如此,我们将一种通过循环地一次移动某个向量的元素一个位置得到的特殊循环矩阵称为「移位算子」。循环矩阵可以与移位算子交换,这也从另一个侧面说明卷及操作是一种具有移位等变性的操作。我们不仅可以断言每个循环矩阵可以与移位交换,而且可以与移位算子交换的矩阵也一定是循环矩阵。因此,卷积是唯一具有移位等变性的线性操作。
图 48:卷积是一种移位等变性操作
从上面的例子可以看书,我们所提出的几何方法是十分强大的。基本上,我们可以自动地根据对称平移导出卷积。以往,在信号处理领域中,卷积往往被作为一种由群推导出的公式,而并没有人可以很好地解释卷积背后思想的由来。
群论视角
接下来,为了讨论如何形式化地引入几何先验,我们将探究更为一般化的情况,此时需要使用群论的公式。
在此,我们可以将卷积认为是某种模式匹配操作,我们在图像中使用滑动窗口完成该操作。
图 49:卷积=匹配移位后的滤波器
如图 49 所示,我们定义了一种移位操作 T,它可以移动卷积滤波器 ψ。如果我们将 T 和 ψ 的内积作用于在图像 x 上的每一次移位,就可以实现卷积操作。
图 50:卷积=匹配变换后的滤波器
值得注意的是,这个平移群实际上可以通过域中自身的点表示。在更一般的情况下,群中还应该包含群中元素表征 ρ 变换而来的特征。此时,我们可以通过卷积操作就可以作用于群 g 中所有的元素,并得到相应的值。这与欧氏几何中的情况有很大区别。
图 51:球面卷积神经网络
图 51 说明了如何在球面上运用卷积。实际上,球面信号是十分重要的。例如,在统计学中,很多观测数据自然而然地可以在球面上表示(如宇宙微波背景辐射)。在这里,我们给出了一个特殊的旋转群 SO(3),其中的旋转操作保留方向信息,而球面上的异常匹配点可以被表征为正交矩阵 R,其行列式为 1。我们在 SO(3) 群上定义卷积,计算每个滤波器的旋转结果与 x 的内积。
图 52:SO(3) 群上的卷积
因此,如果我们想要在其它层中应用上述卷积操作,只需要将其应用于旋转点的三维流形 SO(3) ,而不需要再应用于球面上。
图 53:齐性空间——全局对称群
上述球面空间是非欧空间的一个例子,我们可以通过对称旋转群中的元素,将球面上的某个点变换为球面上的另一个点。在几何中,我们称这种空间为齐性空间,其关键的特点是具有全局对称结构,而这种全局对称结构并不适用于一般流形。
测地线与规范
图 54:平行移动
值得注意的是,当我们对某张图像应用滑动窗口时,无论我们沿着怎样的路径从某一点滑动到另一点,最终得到的结果是相同的。然而,在流形上,情况就完全不同了。如图 54 所示,当我们分别沿着绿色路径或蓝色路径从点 u 到点 v 时,会得到完全不同的结果。在微分几何中,我们将这种现象称为「平行移动」(parallel transport),即在流行上移动某个向量得到的结果与具体的移动路径相关。
图 55:流形空间与等距群
图 56:测地线 CNN
流形和欧氏空间的一个主要区别在于,流形仅在局部上具有欧几里得空间的性质。我们可以将点 u 的小型领域映射到正切空间中。我们可以在正切空间中使用一种被称为「黎曼度量」的内积结构,从而使我们可以度量长度和角度。当流形发生变形时,在不影响黎曼度量的情况下,这种变形是一种等距变形,它来源于「等距群」。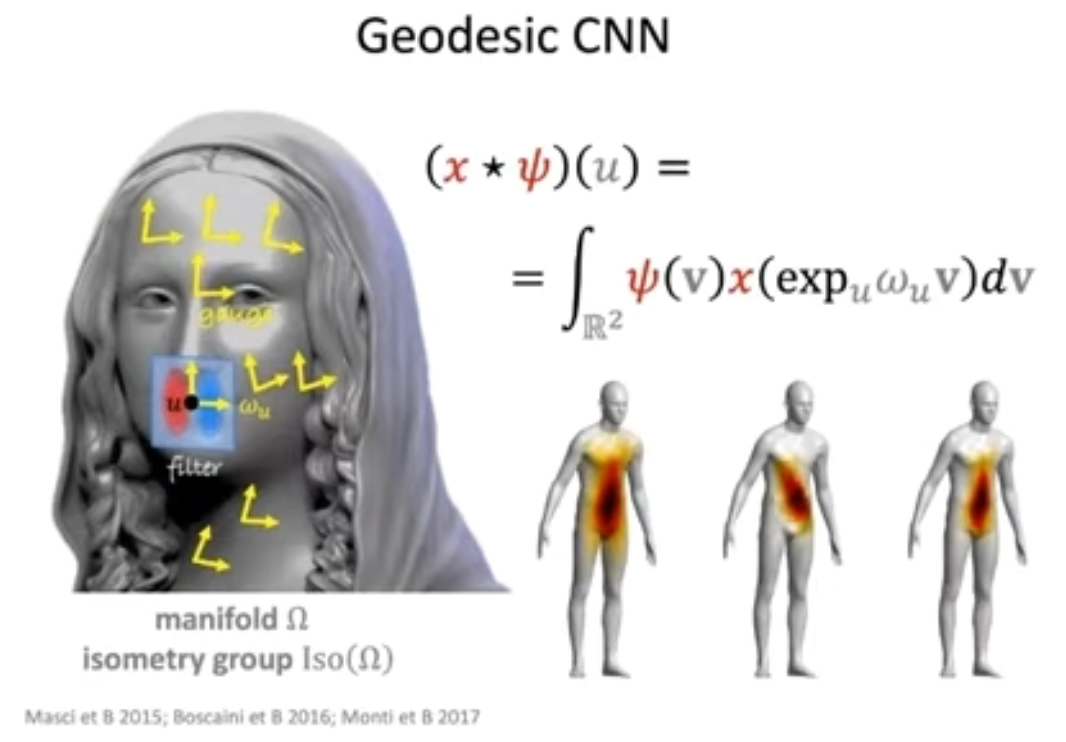
图 57:测地线卷积神经网络
类似地,我们可以定义一个流形上的「卷积」,该操作使用一个应用于正切空间的局部滤波器。如果我们将这种操作构造为一个内在的滤波器,就会得到具有对流形上的等距群的形变不变性的内在滤波器。实际上,这种架构最适合流形上的深度学习,我们将其称为「测地线 CNN」。值得注意的是,由于我们在局部的流形上进行操作,所以并没有使用全局的坐标系统。因此,我们需要在每个点上固定一个局部结构,该结构被物理学家称为「规范」(gauge)。
图 58:规范不变性卷积神经网络
在每一点上,我们都可以通过规范变换任意改变或选择这种规范,这种变换通常是一种保持位置或局部方向的旋转。我们需要以相同的方式变换,考虑滤波器上的规范变换的影响,这种滤波器具有规范等变性。可见,这一过程也遵循了集合深度学习的设计准则,要么利用了等距群的不变性,要么使用了一种微妙的流形上的结构群的不变性。
图 59:欧式卷积和几何卷积
在计算机视觉和图形学领域中,我们往往将二维流形或曲面离散化成矩阵,并将其作为对 3D 物体建模的标准方式。我们可以从几何的角度改进这一过程,设计可以从物体内部定义的滤波器。这使深度学习架构具备对非弹性形变的不变性。我们处理可形变物体的一个关键应用是:动作捕捉(Mocap)。这种技术被用于制作「阿凡达」这种昂贵的商业大片。
图 60:人脸形状分析和合成
在该问题中,涉及到计算机视觉中的两个单行问题。首先,在给定传感器捕获的带有噪声的人脸后,我们需要将其与规范的人脸模型对应,从而进行形状分析。此外,我们有时需要需要对该模型进行变形,从而合成出输入的演员的人脸。
图 61:英特尔
十年前,Michael Brosteim 坚信我们将会用到生成这种动作捕捉结果的 3D 传感器。由于那时没有这种便宜、实时,且具有足够分辨率的传感器,Michael 等人成立了名为「Invision」的初创公司,他们在 2011 年使用 FPGA 首次实现了这种传感器的原型。此后,该公司被英特尔集团收购,并成立了英特尔「实感」(real sense)技术部门。Michael 也在随后的 8 年间投身于这一技术的研发,这也是首个大规模量产的集成 3D 传感器。
图 62:根据 2D 图像重建 3D 手模型
十年之后的今天,我们并不需要与前文所述的动作捕捉技术相类似的输入。我们可以使用一种混合的几何深度学习架构用于 3D 形状合成。在如图 50 所示的架构汇总,我们使用标准的 2D 编码器,其输入为一张图片或一段视频,而几何解码器可以重建一个相应的 3D 模型。
图 63:Kulon 的 3D 人手重建器
在 CVPR 2020 上,Michael 的博士生 Kulon 与初创公司「Ariel AI」合作,利用完全来自输入视频的弱监督信息研发了一种人手的 3D 重建器。该系统在 iPhone 10 上的运行速度比之前提升了 10 倍。
几何深度学习的应用
图 64:图——关系和交互的系统
图数据无处不在,我们几乎可以使用图来描述任何关系和交互的系统(从纳米级的分子结构,到微观的分子之间的相互作用,再到宏观的全国乃至全世界的社交网络)。
图 65:社交网络中的错误信息检测
如今,在与社交网络有关的流行媒体中,往往会出现错误信息或所谓的「假新闻」。相当多的经验证据表明,假新闻在社交网络上以不同的方式传播。我们试图通过使用图学习,观察传播模式来检测 Twitter 上的错误信息,得到了令人鼓舞的结果。2019 年 Michael 及其学生创办「FABULA AI」公司将这项技术商业化,且被 Twitter 收购。目前,Michael 领导了 Twitter 的图机器学习研究组。他们分析的对象包括照片,社交网络等图数据。这些技术在恶意用户检测、推荐助手等场景下得到了使用。
图 66:药物发现与设计
然而,在 Michael 看来,生命科学和药物设计是几何深度学习最有可能大放异彩的研究领域。研制新药是一个需要耗费大量时间和金钱的过程,将某种新药推向市场往往需要花费数十年的时间以及超过十亿美金的资金。其原因之一是,药品在各个阶段的测试成本太高。可以通过化学方法合成的分子组成的药物空间十分巨大,而我们可以在实验室中往往仅仅只能测试其中的几千种药品,二者之间存在巨大的鸿沟。
图 67:虚拟药物筛选
我们可以通过计算的方法对候选分子进行某种形式的筛选,预测分子的属性(如毒性和亲和力)的目标。最近,图神经网络在虚拟药物筛选领域取得了令人瞩目的成就。如今,我们已经有了比以前使用的传统方法更准确、更有序的分子筛选方式。
图 68:通过图神经网络发现新型抗生素
2020 年,MIT 的研究人员将图神经网络用于预测不同分子的抗生素活性,从而发现了一种新型强大抗生素,该药物可以被用于治疗糖尿病。Covid-19 的蔓延证明了人类面对新的病原体是十分脆弱的。如今,一些细菌已经对抗生素产生了耐药性,人们需要不断研制新的抗生素。
图 69:蛋白质相互作用——PPI
如图 69 所示,在研制一些传统的小分子药物时,往往会在其表面设计一些标靶附着的口袋状区域,而标靶往往是一些蛋白质分子。近年来,由于我们体内大多数生物过程(包括与疾病相关的过程)都涉及到相互作用的蛋白质,商业公司的研究兴趣逐渐转向了对蛋白质相互作用(PPI)由破坏和抑制效果的药物。其中,最为著名的机制就是癌症的免疫疗法,该工作获得了 2018 年的诺贝尔奖。如图 69 中所示的 PD-L1,拥有较为光滑的受体的 PPI往往对于传统的小分子是无成药性的。
图 70:从头设计蛋白质
研究人员基于大分子,多肽,蛋白质,或抗体,通过工程技术设计一类具有应用前景的新药,以解决这些困难的标靶。这类药物被称为生物药物,目前已经有部分此类药物被投向市场。对于某些十年前被认为是「不治之症」的癌症,目前也许可以使用生物药物作为治疗方案。Michael 与其来自洛桑联邦理工学院的研究者一起研发了一种几何深度学习方法——MaSIF,它可以从头开始设计药物,并且成为了「Nature Methods」的封面文章。如图 70 所示的三种蛋白质都被证明可以结合肿瘤靶点 PD-L1。
图 71:药物的重定位&组合疗法
「药物的重定位」当下另一个非常具有前景的研究方向,这是一种更廉价、更迅速的治疗方法。通过该方法,我们可以将现有的安全的药物用于新的靶点。有时,与也会配合使用其它的药物,这被称为组合疗法或多药疗法。许多这样的药物组合可能存在未知的或潜在的危险作用,而研究人员最近也将图神经网络用于预测药物的副作用。药物的组合可能存在一些问题,它们可能是相互矛盾的。Michael 近期也深度参与了一项寻找抗病毒感染的药物组合的工作。
图 72:蛋白质设计与食物
这种思想不仅仅可以被用于药物分子合成,Michael 等人也将基于图的药物监管方法应用于食品领域。某些基于植物的食物成分中的化合物与抗癌药物的化学成分是相同的,我们吃的每一口食物都含有数千个这样的分子。而这些食物并不会被监管机构追踪,他们是营养领域的「暗物质」。



往期精彩必读文章(单击就可查看):
1.谷歌突然宣布:上帝的密码防线逐渐崩溃!人工智能有可能是人类文明史的终结!
2.人工智能的现状与未来
3. 国防科技大学教授:殷建平——计算机科学理论的过去、现在与未来
4.图灵奖得主Hamming的22年前经典演讲:如何做研究,才能不被历史遗忘
5.当这位70岁的Hinton老人还在努力推翻自己积累了30年的学术成果时,我才知道什么叫做生命力(附Capsule最全解析)
6.科学正在证明,科学并不科学
7.沉痛!中国半导体 ”芯酸“史!
8.数学的深渊
9. 计算的极限(续)
10.计算的极限
11.高考大数据:哪个省才是高考地狱模式?结论和想象不太一样
12.老婆离家三周,我写了一个操作系统!