前文(机器学习算法 - 随机森林之决策树初探(1))讲述了决策树的基本概念、决策评价标准并手算了单个变量、单个分组的Gini impurity。是一个基本概念学习的过程,如果不了解,建议先读一下再继续。
本篇通过 R 代码(希望感兴趣的朋友能够投稿这个代码的Python实现)从头暴力方式自写函数训练决策树。之前计算的结果,可以作为正对照,确定后续函数结果的准确性。
训练决策树 - 确定根节点的分类阈值
Gini impurity可以用来判断每一步最合适的决策分类方式,那么怎么确定最优的分类变量和分类阈值呢?
最粗暴的方式是,我们用每个变量的每个可能得阈值来进行决策分类,选择具有最低Gini impurity值的分类组合。这不是最快速的解决问题的方式,但是最容易理解的方式。
定义计算Gini impurity的函数
data y=c(1,0.5,1.5,2.1,2.8,2,2.2,3,3.3,3.5),
color=c(rep('blue',3),rep('red',2),rep('green',5)))
data
## x y color
## 1 0.0 1.0 blue
## 2 0.5 0.5 blue
## 3 1.1 1.5 blue
## 4 1.8 2.1 red
## 5 1.9 2.8 red
## 6 2.0 2.0 green
## 7 2.5 2.2 green
## 8 3.0 3.0 green
## 9 3.6 3.3 green
## 10 3.7 3.5 green
首先定义个函数计算每个分支的Gini_impurity。
Gini_impurity # print(branch)
len_branch if(len_branch==0){
return(0)
}
table_branch wrong_probability return(sum(sapply(table_branch, wrong_probability, total=len_branch)))
}
测试下,没问题。
Gini_impurity(c(rep('a',2),rep('b',3)))
## [1] 0.48
再定义一个函数,计算每次决策的总Gini impurity.
Gini_impurity_for_split_branch class_column, Init_gini_impurity=NULL){
total = nrow(data)
left left_len = length(left)
left_table = table(left)
left_gini
right =threshold,][[class_column]]
right_len = length(right)
right_table = table(right)
right_gini total_gini
result = c(variable_column,threshold,
paste(names(left_table), left_table, collapse="; ", sep=" x "),
paste(names(right_table), right_table, collapse="; ", sep=" x "),
total_gini)
names(result)
if(!is.null(Init_gini_impurity)){
Gini_gain result = c(variable_column, threshold,
paste(names(left_table), left_table, collapse="; ", sep=" x "),
paste(names(right_table), right_table, collapse="; ", sep=" x "),
Gini_gain)
names(result) }
return(result)
}
测试下,跟之前计算的结果一致:
as.data.frame(rbind(Gini_impurity_for_split_branch(2, data, 'x', 'color'),
Gini_impurity_for_split_branch(2, data, 'y', 'color')))
## Variable Threshold Left_branch Right_branch Gini_impurity
## 1 x 2 blue x 3; red x 2 green x 5 0.24
## 2 y 2 blue x 3 green x 5; red x 2 0.285714285714286
暴力决策根节点和阈值
基于前面定义的函数,遍历每一个可能的变量和阈值。
首先看下基于变量x的计算方法:
uniq_x delimiter_x impurity_x data=data, variable_column='x', class_column='color')))
print(impurity_x)
## Variable Threshold Left_branch Right_branch Gini_impurity
## 1 x 0.25 blue x 1 blue x 2; green x 5; red x 2 0.533333333333333
## 2 x 0.8 blue x 2 blue x 1; green x 5; red x 2 0.425
## 3 x 1.45 blue x 3 green x 5; red x 2 0.285714285714286
## 4 x 1.85 blue x 3; red x 1 green x 5; red x 1 0.316666666666667
## 5 x 1.95 blue x 3; red x 2 green x 5 0.24
## 6 x 2.25 blue x 3; green x 1; red x 2 green x 4 0.366666666666667
## 7 x 2.75 blue x 3; green x 2; red x 2 green x 3 0.457142857142857
## 8 x 3.3 blue x 3; green x 3; red x 2 green x 2 0.525
## 9 x 3.65 blue x 3; green x 4; red x 2 green x 1 0.577777777777778
再包装2个函数,一个计算单个变量为决策节点的各种可能决策的Gini impurity,
另一个计算所有变量依次作为决策节点的各种可能决策的Gini impurity。
Gini_impurity_for_all_possible_branches_of_one_variable uniq_value delimiter_value impurity Gini_impurity_for_split_branch, data=data,
variable_column=variable,
class_column=class,
Init_gini_impurity=Init_gini_impurity)))
if(is.null(Init_gini_impurity)){
decreasing = F
} else {
decreasing = T
}
impurity return(impurity)
}
Gini_impurity_for_all_possible_branches_of_all_variables one_split_gini Gini_impurity_for_all_possible_branches_of_one_variable,
data=data, class=class,
Init_gini_impurity=Init_gini_impurity))
if(is.null(Init_gini_impurity)){
decreasing = F
} else {
decreasing = T
}
one_split_gini[order(one_split_gini[[colnames(one_split_gini)[5]]], decreasing = decreasing),]
}
测试下:
Gini_impurity_for_all_possible_branches_of_one_variable(data, 'x', 'color')
## Variable Threshold Left_branch Right_branch Gini_impurity
## 5 x 1.95 blue x 3; red x 2 green x 5 0.24
## 3 x 1.45 blue x 3 green x 5; red x 2 0.285714285714286
## 4 x 1.85 blue x 3; red x 1 green x 5; red x 1 0.316666666666667
## 6 x 2.25 blue x 3; green x 1; red x 2 green x 4 0.366666666666667
## 2 x 0.8 blue x 2 blue x 1; green x 5; red x 2 0.425
## 7 x 2.75 blue x 3; green x 2; red x 2 green x 3 0.457142857142857
## 8 x 3.3 blue x 3; green x 3; red x 2 green x 2 0.525
## 1 x 0.25 blue x 1 blue x 2; green x 5; red x 2 0.533333333333333
## 9 x 3.65 blue x 3; green x 4; red x 2 green x 1 0.577777777777778
两个变量的各个阈值分别进行决策,并计算Gini impurity,输出按Gini impurity由小到大排序后的结果。根据变量x和阈值1.95(与上面选择的阈值2获得的决策结果一致)的决策可以获得本步决策的最好结果。
variables Gini_impurity_for_all_possible_branches_of_all_variables(data, variables, class="color")
## Variable Threshold Left_branch Right_branch Gini_impurity
## 5 x 1.95 blue x 3; red x 2 green x 5 0.24
## 3 x 1.45 blue x 3 green x 5; red x 2 0.285714285714286
## 31 y 1.75 blue x 3 green x 5; red x 2 0.285714285714286
## 4 x 1.85 blue x 3; red x 1 green x 5; red x 1 0.316666666666667
## 6 x 2.25 blue x 3; green x 1; red x 2 green x 4 0.366666666666667
## 41 y 2.05 blue x 3; green x 1 green x 4; red x 2 0.416666666666667
## 2 x 0.8 blue x 2 blue x 1; green x 5; red x 2 0.425
## 21 y 1.25 blue x 2 blue x 1; green x 5; red x 2 0.425
## 51 y 2.15 blue x 3; green x 1; red x 1 green x 4; red x 1 0.44
## 7 x 2.75 blue x 3; green x 2; red x 2 green x 3 0.457142857142857
## 71 y 2.9 blue x 3; green x 2; red x 2 green x 3 0.457142857142857
## 61 y 2.5 blue x 3; green x 2; red x 1 green x 3; red x 1 0.516666666666667
## 8 x 3.3 blue x 3; green x 3; red x 2 green x 2 0.525
## 81 y 3.15 blue x 3; green x 3; red x 2 green x 2 0.525
## 1 x 0.25 blue x 1 blue x 2; green x 5; red x 2 0.533333333333333
## 11 y 0.75 blue x 1 blue x 2; green x 5; red x 2 0.533333333333333
## 9 x 3.65 blue x 3; green x 4; red x 2 green x 1 0.577777777777778
## 91 y 3.4 blue x 3; green x 4; red x 2 green x 1 0.577777777777778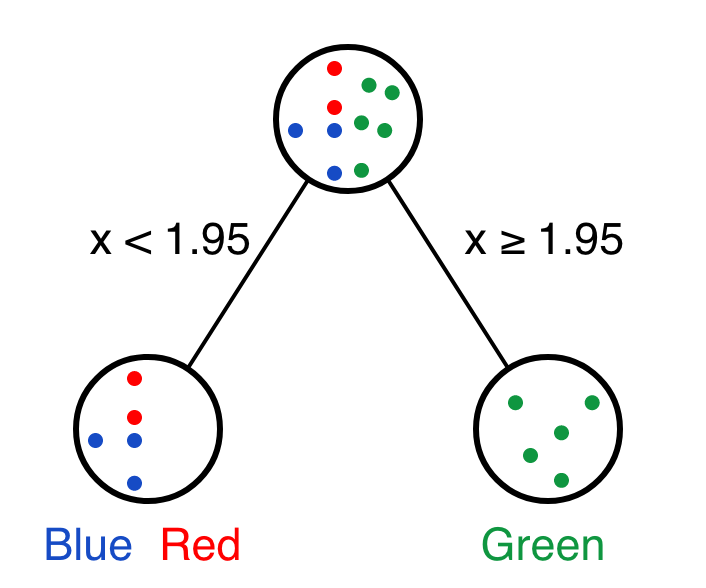
https://victorzhou.com/blog/intro-to-random-forests/
https://victorzhou.com/blog/gini-impurity/
https://stats.stackexchange.com/questions/192310/is-random-forest-suitable-for-very-small-data-sets
https://towardsdatascience.com/understanding-random-forest-58381e0602d2
https://www.stat.berkeley.edu/~breiman/RandomForests/reg_philosophy.html
https://medium.com/@williamkoehrsen/random-forest-simple-explanation-377895a60d2d
往期精品(点击图片直达文字对应教程)
后台回复“生信宝典福利第一波”或点击
阅读原文获取教程合集