Abstract
昨天我们完成了一部分神经网络的数学推导,今天,我们来尝试一下第一步,将激活函数换为sigmoid函数,然后拟合函数曲线,因为今天有点事,就只写一部分吧
Introduction
其实本质上,这个工作只是更换损失函数,我们原本的判断依据是 错误分类的点到超平面的总距离,然后使得这个距离为0,而如果是做函数拟合,就大概率不存在这个0距离,我们只能使得它尽可能地为0,或者说求最小值,先来看看数学表达,拟合曲线为
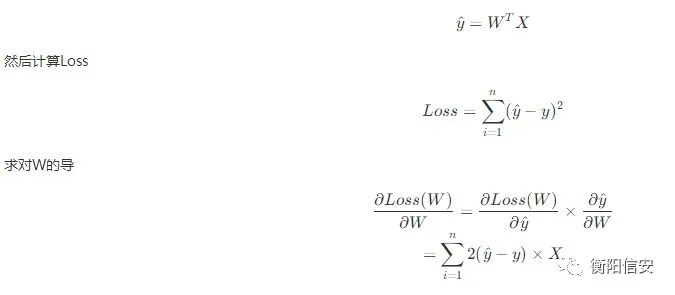
OK,我们的目标就是求Loss的最小值,也就是使得偏导接近0,还是使用SGD来实现
Implementation
Basic Framework
直接改之前的代码,保留一个大概的框架
import numbers
class Vector:
#Ignore Detail Implmentation
class LinearFitting:
def __init__(self):
self.x, self.y = [], []
self._eta = 0
self.omega = 0
pass
def eta(self, eta):
self._eta = eta
def fit(self, x, y):
if len(x) != len(y):
raise Exception("x and y has different rows")
if len(x) == 0:
raise Exception("can use a empty dataset")
self.x = x
self.y = y
self._train()
def _get_result(self):
return self.omega.to_array()
def _train(self):
#initial of basic parameter η0
pass
if __name__ == "__main__":
pass
Detail Implementation
由于其实公式都出来了,SGD我们之前也讲过详细实现了,所以现在其实没必要讲那么多,直接对代码下手吧
import numbers
from math import sqrt, pow
class Vector:
def __init__(self, data):
self._list = []
for i in data:
self._list.append(i)
def __str__(self):
return 'Vector(' + ','.join([str(i) for i in self._list]) + ')'
def __add__(self, b):
def cb(i, v):
result.set(i, result.get(i) + v)
if self.dimension() != b.dimension():
raise Exception("vector add method requires the same dimension")
result = Vector(self._list)
b.walk(cb)
return result
def __sub__(self, b):
return self + b * -1
def __mul__(self, b):
if isinstance(b, numbers.Real):
return Vector([self.get(i) * b for i in range(self.dimension())])
if self.dimension() != b.dimension():
raise Exception("vector add method requires the same dimension")
result = 0
for i in range(self.dimension()):
result += self.get(i) * b.get(i)
return result
def dimension(self):
return len(self._list)
def walk(self, cb):
for i in range(len(self._list)):
cb(i, self._list[i])
def get(self, idx):
if idx >= self.dimension():
raise Exception("idx out of bound")
return self._list[idx]
def set(self, idx, val):
if idx >= self.dimension():
raise Exception("idx out of bound")
self._list[idx] = val
def to_array(self):
return [i for i in self._list]
def l2(self):
result = 0
for i in self._list:
result += i * i
return sqrt(result)
def clone(self):
return Vector(self._list)
def append(self, v):
self._list.append(v)
return self
class LinearFitting:
def __init__(self):
self.x, self.y = [], []
self._eta = 1
self.omega = 0
self.CONSTS_ZERO = 0.0001
pass
def eta(self, eta):
self._eta = eta
def fit(self, x, y):
if len(x) != len(y):
raise Exception("x and y has different rows")
if len(x) == 0:
raise Exception("can use a empty dataset")
self.x = [i.clone().append(1) for i in x]
self.y = y
self._train()
def _caculate(self, x):
return x * self.omega
def _is_fitting(self, derivative):
if isinstance(derivative, Vector):
return derivative.l2() < self.CONSTS_ZERO
return abs(derivative) < self.CONSTS_ZERO
def _get_result(self):
return self.omega.to_array()
def _train(self):
# initial omega
self.omega = Vector([0] * self.x[0].dimension())
while True:
# caculate square mean and check whether fitting
smean = 0
for i, v in enumerate(self.x):
yhat = self._caculate(v)
y = self.y[i]
smean += pow((yhat - y), 2)
print(f'square mean:{smean}')
print(f'ω:{self.omega}')
derivative = Vector([0] * self.x[0].dimension())
for i, v in enumerate(self.x):
yhat = self._caculate(v)
y = self.y[i]
derivative += v * 2 * (yhat - y)
if self._is_fitting(derivative):
return
# SGD
self.omega -= derivative * self._eta
if __name__ == "__main__":
datasets = [
Vector([2]),
Vector([3]),
Vector([4])
]
values = [
2,
3,
4,
]
l = LinearFitting()
l.eta(0.001)
l.fit(datasets, values)
然后我们就碰到了SGD的第一个也是特别致命的问题:学习率到底怎么设置,在我们的例子里,我们将学习率设置到了0.001才训练成功,如果学习率高一点的话,训练会陷入死循环,为什么?考虑一个模型

第一次计算平方差为29,偏导为(-58,-18),这意味着什么?通过梯度下降,下一次W会变成58,b变成18,这一下子就变得太大了,这还没完,下一次,会变得更大。。或者太小,看起来的效果就是下面这样子
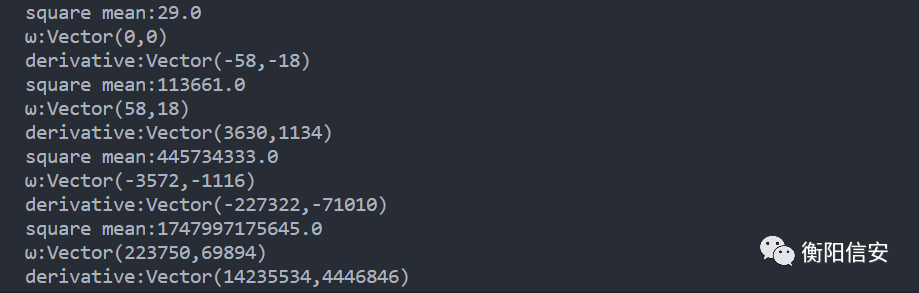
直接打出寄,所以这就是为什么需要《调参工程师》,我们使得学习率为一个理想的数,这里我使用0.001成功了,代价就是训练速度很慢,5秒才出结果当然啊

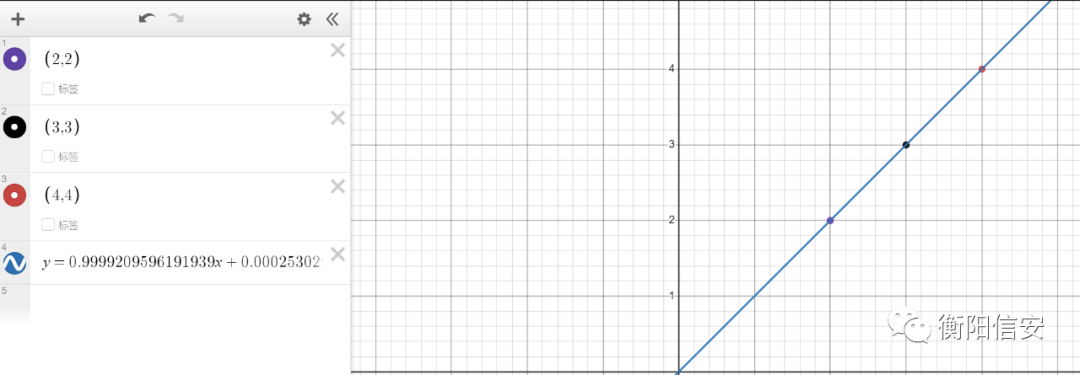

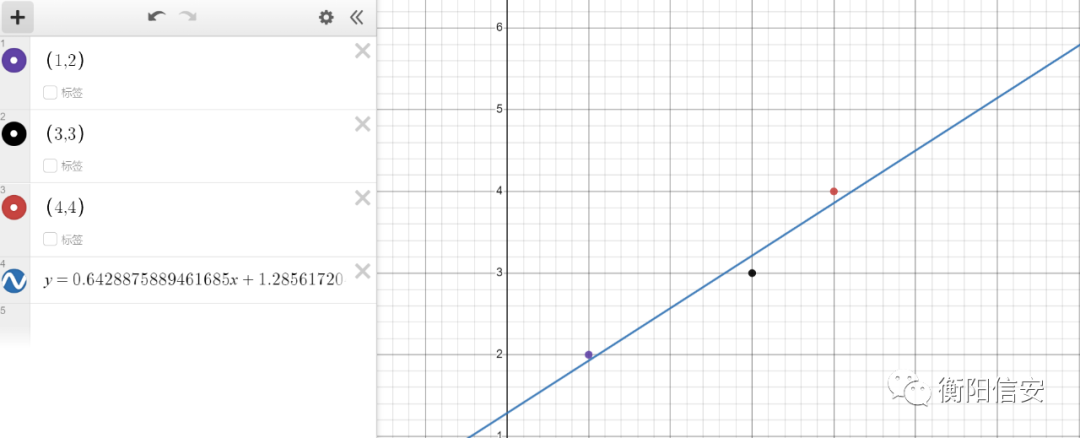
我们相信,后面我们会解决它的
Eta Problem
我们这里先尝试一个方案:即不人工指定学习率η,而是自适应η,从现有数据来看,我们该怎么决定η?如果经过一次调整以后的Loss不变小,反而变大,那么我们可以认为是学习率太大了,稍微推导一下吧,有公式的帮助会好很多

只要确保Δ的影响不会使得变号,就可以保证在Loss在变小,而Δ本身是受到梯度影响的,它会使得在同号的时候让Loss变小,但是很明显,我们的η是一个标量,它不能针对每一项都使得Δ有正面影响,那可以让η为向量吗?也不行,因为η最终影响的是ω,如果用向量的话,η应该和ω拥有相同的项数,但是要让每一项的Δ都为正就需要拥有n个项,很明显,这两者不相等,做的都不是一个维度的计算,单看数学的话也不行,它们的意义都不一样,所以我们只能使得η为一个标量,而我们评估Loss(W1)和Loss(W2),如果不降反增,就说明了η太大,但是如果变化太小了,就说明η太小,现在的问题就是如何评估变化太小,这个应该是可以通过数学推出来的,但是我太菜了所以先根据经验来判断,我就单纯尝试一下,就加入了几行
if smean - prev_smena > 0:
self._eta /= 2
prev_smena = smean
效果立竿见影,训练时间缩短到了8ms,估计很多时间还都是内存IO时间,然后尝试一下复杂一点的训练集,然后马上就发现了问题,由于第一次训练时的eta很大,就会导致初始化的时候w的第一次的值变得很大,从而导致训练时间过长,为了处理这个问题,我们需要在处理eta的时候做点事,总体思想就是在找到合适的η之后重置w,那么也就将训练分为了两个阶段,即η适应期和实际训练期,其实已经可以看出来,η的具体值是适应于当前训练集的,可能因为我的优化问题,我在处理完1000个二维样本点的训练时间高达530s,处理完1000个四位样本点得时间为1345s,=,=,但其实还是可以优化的,包括内存IO在内的一系列优化,这个numpy应该就已经处理得很好了
ω:Vector(3.521100000015364,-93.11999994979733)
ω:Vector(3.5211000000153567,-93.11999994982126)
ω:Vector(3.5211000000153496,-93.11999994984518)
ω:Vector(3.521100000015342,-93.11999994986908)
ω:Vector(3.521100000015335,-93.11999994989299)
ω:Vector(3.5211000000153274,-93.11999994991687)
ω:Vector(3.5211000000153203,-93.11999994994075)
ω:Vector(3.5211000000153128,-93.11999994996461)
ω:Vector(3.5211000000153057,-93.11999994998845)
fitting time -> 530.0819354057312s
完整代码:
import numbers
from math import sqrt, pow
import time
class Vector:
def __init__(self, data):
self._list = []
for i in data:
self._list.append(i)
def __str__(self):
return 'Vector(' + '\t'.join([str(i) for i in self._list]) + ')'
def __add__(self, b):
def cb(i, v):
result.set(i, result.get(i) + v)
if self.dimension() != b.dimension():
raise Exception("vector add method requires the same dimension")
result = Vector(self._list)
b.walk(cb)
return result
def __sub__(self, b):
return self + b * -1
def __mul__(self, b):
if isinstance(b, numbers.Real):
return Vector([self.get(i) * b for i in range(self.dimension())])
if self.dimension() != b.dimension():
raise Exception("vector add method requires the same dimension")
result = 0
for i in range(self.dimension()):
result += self.get(i) * b.get(i)
return result
def dimension(self):
return len(self._list)
def walk(self, cb):
for i in range(len(self._list)):
cb(i, self._list[i])
def get(self, idx):
if idx >= self.dimension():
raise Exception("idx out of bound")
return self._list[idx]
def set(self, idx, val):
if idx >= self.dimension():
raise Exception("idx out of bound")
self._list[idx] = val
def to_array(self):
return [i for i in self._list]
def l2(self):
result = 0
for i in self._list:
result += i * i
return sqrt(result)
def clone(self):
return Vector(self._list)
def append(self, v):
self._list.append(v)
return self
class LinearFitting:
def __init__(self):
self.x, self.y = [], []
self._eta = 1
self.omega = 0
self.CONSTS_ZERO = 0.0001
pass
def eta(self, eta):
self._eta = eta
def fit(self, x, y):
if len(x) != len(y):
raise Exception("x and y has different rows")
if len(x) == 0:
raise Exception("can use a empty dataset")
self.x = [i.clone().append(1) for i in x]
self.y = y
self._train()
def caculate(self, x):
return self._caculate(x)
def _caculate(self, x):
return x * self.omega
def _is_fitting(self, derivative):
if isinstance(derivative, Vector):
return derivative.l2() < self.CONSTS_ZERO
return abs(derivative) < self.CONSTS_ZERO
def _get_result(self):
return self.omega.to_array()
def _train_eta(self):
self.omega = Vector([0] * self.x[0].dimension())
prev_smean = 99999999999999999999999999999
success = 0
while True:
# caculate square mean and check whether fitting
smean = 0
for i, v in enumerate(self.x):
yhat = self._caculate(v)
y = self.y[i]
smean += pow((yhat - y), 2)
derivative = Vector([0] * self.x[0].dimension())
for i, v in enumerate(self.x):
yhat = self._caculate(v)
y = self.y[i]
derivative += v * 2 * (yhat - y)
print(smean, prev_smean)
if smean - prev_smean > 0:
self._eta *= 0.9
success = 0
else:
success += 1
if success > 10:
break
prev_smean = smean
print(f'eta:{self._eta}')
if smean > 1.7257200647647234e+151:
self.omega = Vector([0] * self.x[0].dimension())
success = 0
else:
self.omega -= derivative * self._eta
def _train(self):
self._train_eta()
# initial omega
self.omega = Vector([0] * self.x[0].dimension())
while True:
# caculate square mean and check whether fitting
smean = 0
for i, v in enumerate(self.x):
yhat = self._caculate(v)
y = self.y[i]
smean += pow((yhat - y), 2)
derivative = Vector([0] * self.x[0].dimension())
for i, v in enumerate(self.x):
yhat = self._caculate(v)
y = self.y[i]
derivative += v * 2 * (yhat - y)
prev_smena = smean
print(f'ω:{self.omega}')
if self._is_fitting(derivative):
return
self.omega -= derivative * self._eta
if __name__ == "__main__":
datasets = []
values = []
def y(x):
return Vector([3.5211, 8.111, -9999.212, -93.12]) * x.clone().append(1)
from random import random
def randomfloat(start, end):
return ((random() * 1000000) % (end - start)) + start
for i in range(1000):
x = Vector([randomfloat(-100, 100),randomfloat(-100, 100),randomfloat(-100, 100)])
datasets.append(x)
values.append(y(x))
l = LinearFitting()
start_time = time.time()
l.fit(datasets, values)
end_time = time.time()
print(f'fitting time -> {end_time - start_time}s')
效果还是不过的,就是时间久了点,我们之后学着继续优化
ω:Vector(3.5211000000132624 8.111000000017365 -9999.211999999998 -93.11999995002158)
Postscript
后来我调整了训练η时的倍率,调整以后同样的训练集的训练时间可以缩短几十倍,上面那个1000s的缩短到了,到了最后还是变成了调参工程师

团队学习笔记分享!

