Abstract
在昨天的初步接触ML以后,我们实现了一个简单的线性模型,它可以做到简单地去拟合一根直线,但是这个直线远远不够,所以从这次开始,我们开始接触更广泛的回归模型并且可视化数据,同时,我们这节还需要学习数据处理,主要是基于pandas的数据处理
Asking the right question of your data
这次我们的数据不再使用之前的糖尿病数据,而是使用美国农协会的某一年的南瓜数据,包括了南瓜产地、日期、价格等等数据,我们需要使用这些数据去预测未来的价格
ML-For-Beginners/US-pumpkins.csv at main · microsoft/ML-For-Beginners (github.com)
Exercise - analyze the pumpkins data
使用pandas这个库来读取excel的数据,这个库其实挺简单的,就是提供了数据表格到python的接口
import pandas as pd
fp = str(pathlib.Path(__file__).parent.resolve())
pumpkins = pd.read_csv(fp + '/US-pumpkins.csv')
frame = pumpkins.head()
我们会输出frame会得到这个表格的前5行数据,展示出来大概如下
接下来,我们想一想价格和日期的关系,很容易就能猜到,其实和年份的关系没有那么多,排除掉如洪涝之类的因素,月份应该才是关键,所以现在我们需要对数据进行预处理,在原始数据中添加月份数据
pumpkins['Month'] = pumpkins.apply(lambda x : x['Date'].split('/')[0], axis=1)
接着,现在的列太多了,我们只需要其中的一部分,比如说价格、最高价、最低价、日期之类的,所以,接着我们过滤出需要的那一部分
import pathlib
import pandas as pd
fp = str(pathlib.Path(__file__).parent.resolve())
pumpkins = pd.read_csv(fp + '/US-pumpkins.csv')
pumpkins['Month'] = pumpkins.apply(lambda x : x['Date'].split('/')[0], axis=1)
selected_columns = ['Package', 'Month', 'Low Price', 'High Price', 'Date']
pumpkins = pumpkins.drop([i for i in pumpkins.columns if i not in selected_columns], axis=1)
print(pumpkins)
接着,我们只有一个最高价和最低价,并没有实际的价格,所以我们需要预估一下当月的平均价格,这个就简单使用取个中间值吧
pumpkins['Price'] = pumpkins.apply(lambda x : (x['Low Price'] + x['High Price']) / 2, axis=1)
然后就是吧,还有一堆的坑,比如说这个数据表格它的单位还不一样,有的是按个算,有的是按盒算,还有的是按半个算。。所以还需要接着处理数据,其实就是统一单位
pumpkins = pumpkins[pumpkins['Package'].str.contains('bushel', case=True, regex=True)]
pumpkins['Price'] = pumpkins.apply(lambda x : (x['Low Price'] + x['High Price']) / 2, axis=1)
pumpkins.loc[pumpkins['Package'].str.contains('1 1/9'), 'Price'] = pumpkins['Price']/(1 + 1/9)
pumpkins.loc[pumpkins['Package'].str.contains('1/2'), 'Price'] = pumpkins['Price']/(1/2)
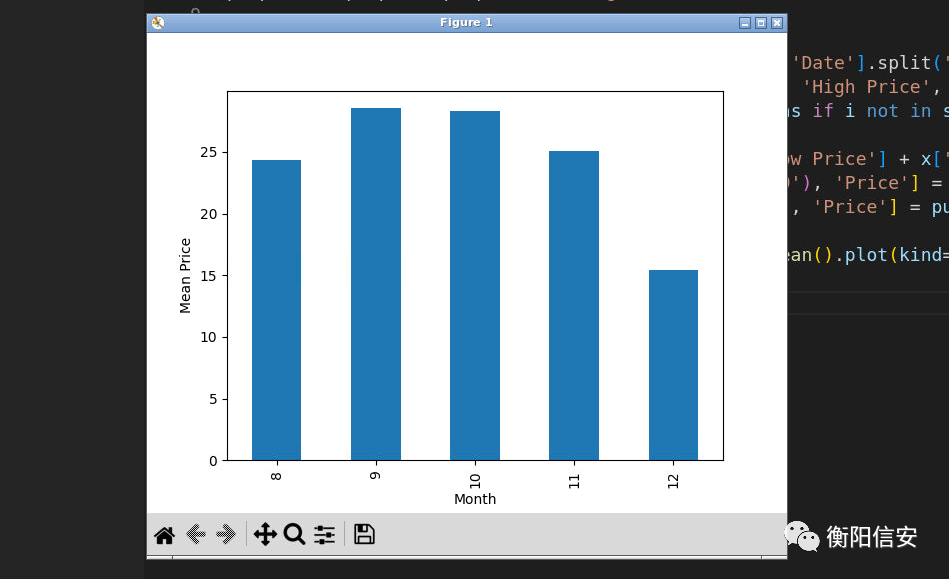
搞了这么多,终于可以开始尝试训练模型了,首先还是展示数据,我们有很多年的数据,我们需要把每一年的数据的各个月加起来算平均值,也就是,按月份分组,完成了以后再打印出来
statistics = pumpkins.groupby(['Month'])['Price'].mean().plot(kind='bar')
plt.ylabel('Mean Price')
plt.show()
唯一的缺点就是月份没好好排(改一哈上面的代码就行了,全部的代码如下
import pathlib
import pandas as pd
from matplotlib import pyplot as plt
fp = str(pathlib.Path(__file__).parent.resolve())
pumpkins = pd.read_csv(fp + '/US-pumpkins.csv')
pumpkins = pumpkins[pumpkins['Package'].str.contains('bushel', case=True, regex=True)]
pumpkins['Month'] = pumpkins.apply(lambda x : int(x['Date'].split('/')[0]), axis=1)
selected_columns = ['Package', 'Month', 'Low Price', 'High Price', 'Date']
pumpkins = pumpkins.drop([i for i in pumpkins.columns if i not in selected_columns], axis=1)
pumpkins['Price'] = pumpkins.apply(lambda x : (x['Low Price'] + x['High Price']) / 2, axis=1)
pumpkins.loc[pumpkins['Package'].str.contains('1 1/9'), 'Price'] = pumpkins['Price']/(1 + 1/9)
pumpkins.loc[pumpkins['Package'].str.contains('1/2'), 'Price'] = pumpkins['Price']/(
1/2)
statistics = pumpkins.groupby(['Month'])['Price'].mean().plot(kind='bar')
plt.ylabel('Mean Price')
plt.show()
除了月份,我们还可以看看以年为单位的某一天,其也可以一定程度展示这些关系
代码上的区别也就是改了一点
def parse(x):
dts = [int(c) for c in x.split('/')]
dt = datetime(dts[2], dts[0], dts[1]).timetuple().tm_yday
return dt
pumpkins['Day'] = pumpkins.apply(lambda x : parse(x=x['Date']), axis=1)
不难看出,年末的时候南瓜价格确实比较低,但是!我们需要注意一点,南瓜的种类对南瓜的价格也有很大的影响,所以最好,我们需要把南瓜的种类分个组如下
发现啊,MINIATURE这种类型的南瓜最贵,PIE TYPE最便宜
colors = ['red', 'blue', 'yellow', 'green']
ax = None
for i, v in enumerate(pumpkins['Variety'].unique()):
df = pumpkins[pumpkins['Variety'] == v]
ax = df.plot.scatter('Day', 'Price', ax = ax, label=v, c=colors[i])
plt.show()
上面搞了那么多,现在终于可以开始尝试做计算和预测了,上面其实更多都是做预处理,没有做什么实质上的工作
首先,如果要训练模型,那么首先需要的就是得到x和y(现在还是线性模型,且只考虑单个变量)
那么,分离出时间和价格,同时注意,我们只训练包含PIE TYPE的南瓜!
pie_pumpkins = pumpkins[pumpkins['Variety'] == 'PIE TYPE']
x = pie_pumpkins['Day'].to_numpy().reshape(-1, 1)
y = pie_pumpkins['Price']
虽然还是很迷惑,pandas的DateFrame类重载了[]操作,实现了这样简便的过滤器,确实厉害,和z3很类似,下一步我们知道了,就是创建训练集和测试集,并简单画一下看看
x_train, x_test, y_train, y_test = model_selection.train_test_split(x, y, test_size=0.2, random_state=0)
line_reg = linear_model.LinearRegression()
line_reg.fit(x_train, y_train)
line_pred = line_reg.predict(x_test)
plt.scatter(x_test, y_test)
plt.scatter(x_train, y_train, color='yellow'
)
plt.plot(x_test, line_pred, color='red')
plt.show()
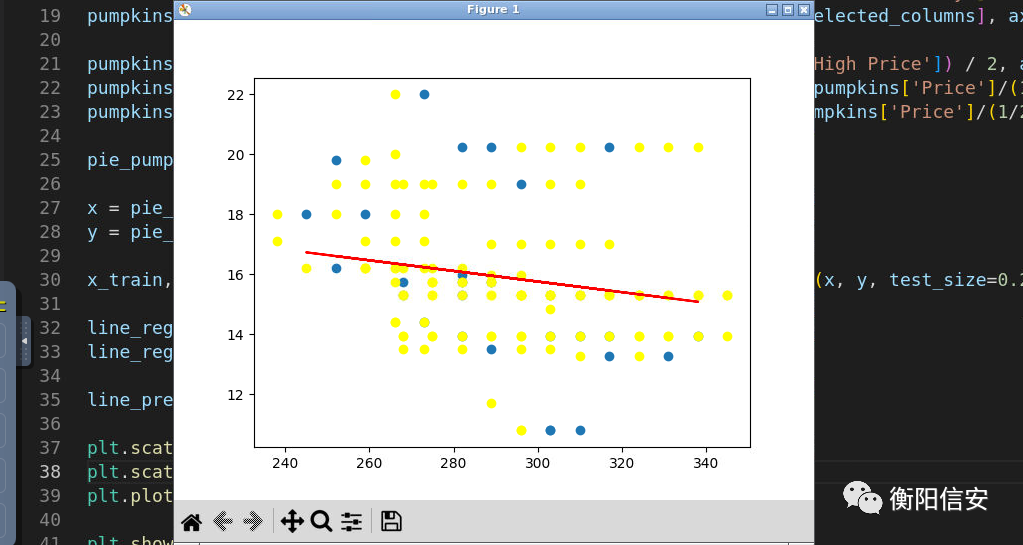
黄色是训练集,蓝色是测试集,我们思考一样,这玩意,它符合线性模型吗????不适合吧,倒不如说,应该是有其他因素的影响(非种类和日期)所以还是有这么大的差异,我们先不管这个影响,试着使用其他的模型,如多项式模型来测试一下
不过我们需要知道的,多项式模型还是可以用线性模型,其基本公式如下
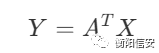
就算是存在如x的平方之类的因素,我们也可以给它简化成
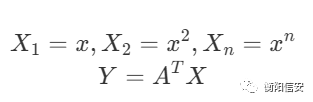
然后sklearn提供的就是pipeline这个东西,我们可以创建一个从PolynomialFeatures到LinearRegression的模型,我们只需要输入一个线性的数据集(这么说可能不太对)就可以得到相应的多维的数据模型,简单说一下就是
我们输入的关系是
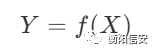
其中X和Y满足
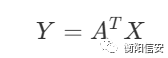
然后经过PolynomialFeatures的处理以后(现在假设为二维),这个关系就可以变成
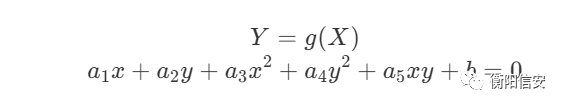
然后x和y存在一个关系,我们可以使用这个线性模型来预测数据,有一说一看到这里的时候我也是挺懵逼的,不过我懵逼的是,这个具体怎么算,不过先不管这个,这个是已经实现好了的
pipeline = make_pipeline(PolynomialFeatures(2), linear_model.LinearRegression())
pipeline.fit(x_train, y_train)
pred = pipeline.predict(x_test)
plt.scatter(x_test, y_test, color='blue')
plt.plot(x_test, pred, color='red')
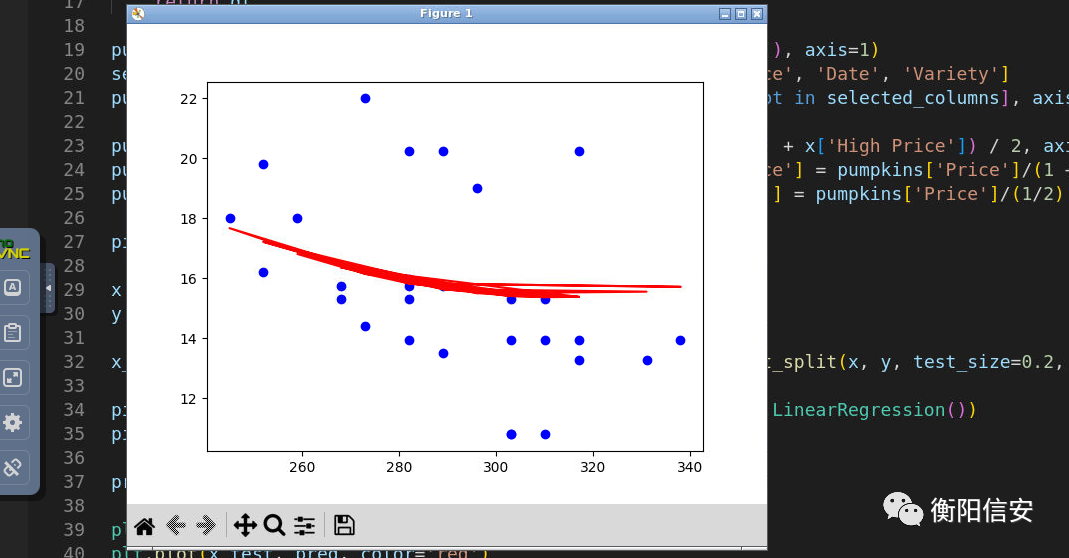
接下来,我们思考一下如何判断我们模型的优劣?这里需要提到两个判据,一个是方差,这个我们很熟悉了,另一个是决定系数(?
先看看方差吧
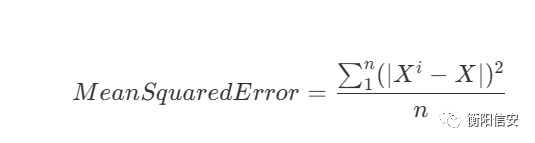
然后我们需要计算他们的百分比来更好地展示它
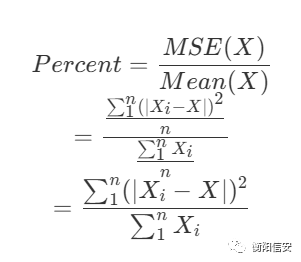
很明显,但这个值越接近0的时候,模型的效果越好
另外一个是决定系数,这玩意的定义如下
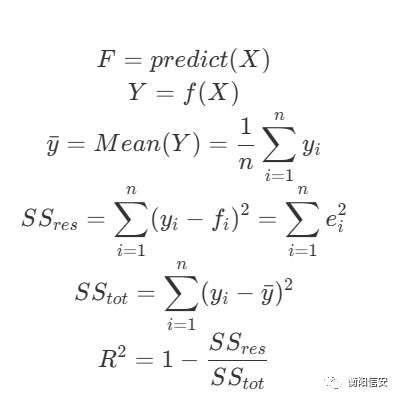
R就是决定系数,我们仔细观察会发现 SS_res是预测值偏差,而 SS_tot 是方差,那也就是,若R越接近1,则yi越接近fi,代表模型效果越好,而若R接近0,则说明偏差越大,而我们上面那个模型的R很小,也就是效果很烂,这其实也正常,可以理解,毕竟维度太少了
最后一步,我们需要尝试多维度,把各个维度的影响都加进来,其实这个线性模型就已经帮我们实现了,毕竟线性模型的表达式如下
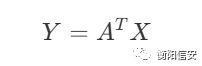
是可以包含多个x的,只需要给x加上一点数据就可以了,同时,将按日分组换位按月分组
def parse(x):
dts = [int(c) for c in x.split('/')]
dt = datetime(dts[2], dts[0], dts[1]).timetuple().tm_mon
return dt
pumpkins['Month'] = pumpkins.apply(lambda x : parse(x=x['Date']), axis=1)
selected_columns = ['Package', 'Month', 'Low Price', 'High Price', 'Date', 'Variety', 'City Name']
pumpkins = pumpkins.drop([i for i in pumpkins.columns if i not in selected_columns], axis=1)
pumpkins['Price'] = pumpkins.apply(lambda x : (x['Low Price'] + x['High Price']) / 2, axis=1)
pumpkins.loc[pumpkins['Package'].str.contains('1 1/9'), 'Price'] = pumpkins['Price']/(1 + 1/9)
pumpkins.loc[pumpkins['Package'].str.contains('1/2'), 'Price'] = pumpkins['Price']/(1/2)
x = pd.get_dummies(pumpkins['Variety']) \
.join(pumpkins['Month']) \
.join(pd.get_dummies(pumpkins['City Name'])) \
.join(pd.get_dummies(pumpkins['Package']))
y = pumpkins['Price']
接下来,训练模型并预测结果
x_train, x_test, y_train, y_test = model_selection.train_test_split(x, y, test_size=0.2, random_state=0)
line_reg = linear_model.LinearRegression()
line_reg.fit(x_train, y_train)
pred = line_reg.predict(x_test)
最后一步,测试决定系数和方差
score = line_reg.score(x_train, y_train)
mse = np.sqrt(mean_squared_error(y_test, pred)) / np.mean(pred)
print(score)
print(mse)
ok,其中,决定系数为0.94,挺高的,喜欢,mse为0.105,挺低的,喜欢,那么就说明我们这个模型还不错~,当然,还可以更高,使用非线性的多项式模型,仅用2维的多项式模型就可以做到决定系数0.97,mse 0.0825
来自团队学习笔记

