【建议收藏】好用的降维算法——t-SNE，带python实例讲解

CDA数据分析师

t-SNE是什么技术

我们直接开门见山好了，第一件事：什么是t-SNE？t-SNE的全称叫做t分布式随机邻居嵌入（t-SNE）。该算法是一种非监督的非线性技术，主要用于数据探索和可视化高维数据。

简而言之，t-SNE为我们提供了数据如何在高维空间中排列的感觉或直觉。它由Laurens van der Maatens和Geoffrey Hinton于2008年开发。

一提到降维，我们会想到大名鼎鼎的PCA，PCA是线性降维的技术，那么较之于我们今天要介绍的t-SNE，它们有什么不同或者联系吗。

如果您熟悉主成分分析（PCA），那么像我一样，你可能想知道PCA和t-SNE之间的区别。

首先要注意的是，PCA是在1933年开发的，而t-SNE是在2008年开发的。自1933年以来，数据科学领域发生了很大变化，主要是在计算和数据大小领域。其次，PCA是一种线性降维技术，旨在最大化方差并保持较大的成对距离。PCA可能导致可视化效果不佳，特别是在处理非线性结构时。这里非线性结构可以视为任何几何形状，如：圆柱体、球、曲线等。

t-SNE与PCA的不同之处在于只保留小的成对距离或局部相似性，而PCA则关注的是保持大成对距离以最大化方差。

图1-“瑞士卷“数据集，保持与t-SNE(实线)的小距离vs最大化方差PCA

Laurens很好地利用上图中的“瑞士卷”数据集很好地说明了PCA和t-SNE方法（实线为t-SNE，虚线为PCA）。你可以看到，由于这个“瑞士卷”数据集（流形）的非线性并保持了大距离，PCA会错误地保留数据的结构。

t—SNE算法原理

现在我们知道为什么有时候我们不用pca而用t-SNE，让我们来看看t-SNE是如何工作的，其背后有怎样的算法原理。其实，概括来说：t-SNE算法计算高维空间和低维空间中一对实例之间的相似性度量。然后，该算法用代价函数来优化这两个相似度指标。这个算法将其分为3个基本步骤。

步骤1:测量高维空间中点之间的相似性

我们以分散在二维空间上的一堆数据点（图2）说明。对于每个数据点（），我们将在该点上以高斯分布为中心。然后，我们测量高斯分布下所有点（）的密度。然后对所有点进行重整化。我们根据高斯得出所有点的概率（）。这些概率与相似之处成正比。这意味着，如果数据点（）和（）在这个高斯圆下具有相等的值，那么它们的比例和相似性是相等的，因此在这个高维空间的结构中具有局部相似性。高斯分布或圆可以使用所谓的复杂度来操作，这影响分布（圆大小）的方差，本质上影响最近邻居的数量。复杂度的正常范围在5到50之间。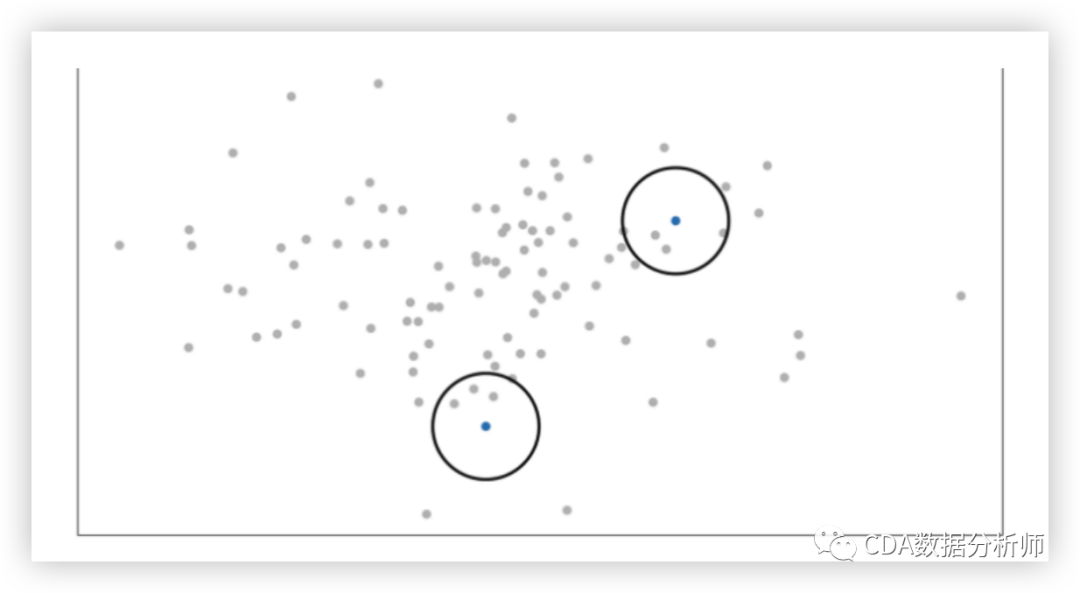

图2-围绕数据点的高斯分布在高维空间中测量成对的相似度

步骤2:第2步类似于第1步，不用高斯分布而是使用具有一定自由度的学生t分布

T分布这也被称为柯西分布（图3）。这给了我们在低维空间中的第二组概率。如您所见，学生t分布的尾部比正态分布更“重”。沉重的尾部可以更好地模拟相距很远的距离。

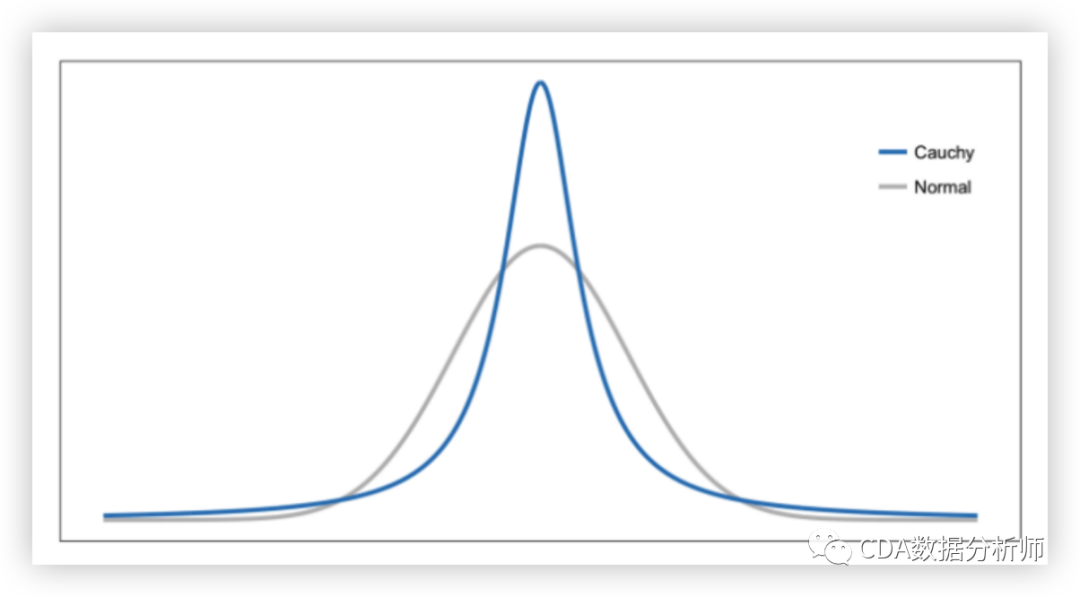
图3-柯西分布和正态分布概率密度图的比较

步骤3:最后一步是，我们希望这些来自低维空间（）的概率集尽可能地反映高维空间（）的概率

我们希望这两个地图结构相似。我们使用库尔巴克-利布勒发散（KL）测量二维空间的概率分布之间的差异。可以有效地比较和值。最后，我们使用梯度下降来最小化我们的KL损失函数。

t-SNE用在哪

现在我们已经了解了t-SNE的工作原理，让我们快速谈谈它在哪里使用。Laurens van der Maaten在他的视频演示中展示了许多例子，他提到了t-SNE在气候研究、计算机安全、生物信息学、癌症研究等领域的使用。也就是说t-SNE可用于高维数据（主要用于可视化），然后这些维度的输出成为其他分类模型的输入。然而，t-SNE不是聚类方法，因为它不保留PCA等输入，并且值可能经常在运行之间发生变化，因此纯粹是为了探索、可视化等工作。

代码示例：

本次案例的目标是通过蘑菇的特征（比如形状、气味等）来区分其是否可以食用，同时会在二维空间上呈现基于PCA和t-SNE的不同的降维分类效果，以此来认识二者的不同。

第1步-导入所需的库，读取并查看数据集

#导入所需的库

import pandas as pd

import numpy as np

import matplotlib.pyplot as plt

import seaborn as sns

#读取并查看数据

data = pd.read_csv('mushrooms.csv')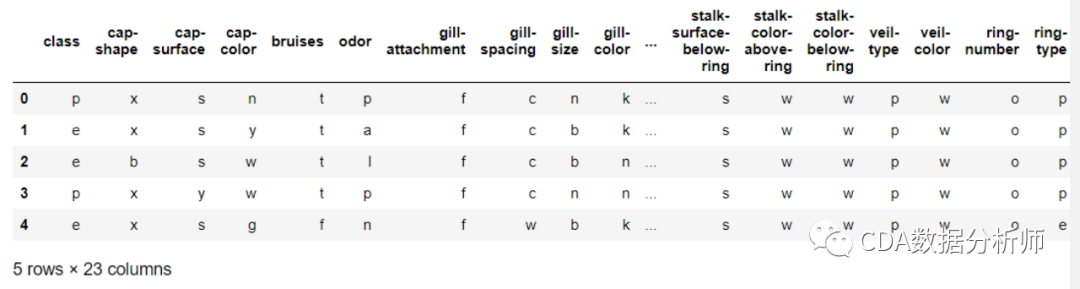

data.head()

第2步-区分解释变量与被解释变量，查看数据的基本信息

#区分解释变量与被解释变量

y = data['class']

X = data.iloc[:,1:]

#查看解释变量的基本信息

X.info()

第3步-查看解释变量的取值情况，进行数据编码

#查看解释变量的取值情况

cols = X.columns.tolist()

for col in cols:

print(col, X[col].unique())

#对解释变量进行数据编码

for col in cols:

X[col] = X[col].astype('category')

X[col] = X[col].cat.codes

X.head()

#删除无用变量

X.drop('veil-type', axis=1, inplace=True)

第4步-PCA降维与可视化

（1）导入所需的库

from sklearn import preprocessing

from sklearn.decomposition import PCA

（2）数据标准化

X_std = preprocessing.scale(X)

（3）pca（二维）

pca=PCA(n_components=2)

pca.fit(X_std)

（4）计算主成分得分，合并数据

X_pca=pd.DataFrame(pca.fit_transform(X_std)).rename(columns={0:'1st_component',1:'2nd_component'})

Y = pd.DataFrame(y)

data_pca = pd.concat([X_pca, Y], axis = 1)

data_pca

（5）可视化PCA降维分类结果

plt.figure(figsize=(8, 8))

sns.scatterplot(data=data_pca, hue='class', x='1st_component', y='2nd_component')

plt.show()

第5步-t-SNE降维与可视化

（1）导入所需的库

from sklearn.manifold import TSNE

（2）t-SNE降维

tsne = TSNE(n_components=2)

tsne.fit(X_std)

（3）可视化t-SNE降维分类结果

X_tsne = pd.DataFrame(tsne.fit_transform(X_std)).rename(columns={0:'dim1', 1:'dim2'})

data_tsne = pd.concat([X_tsne, Y], axis = 1)

plt.figure(figsize=(8, 8))

sns.scatterplot(data=data_tsne, hue='class', x='dim1', y='dim2')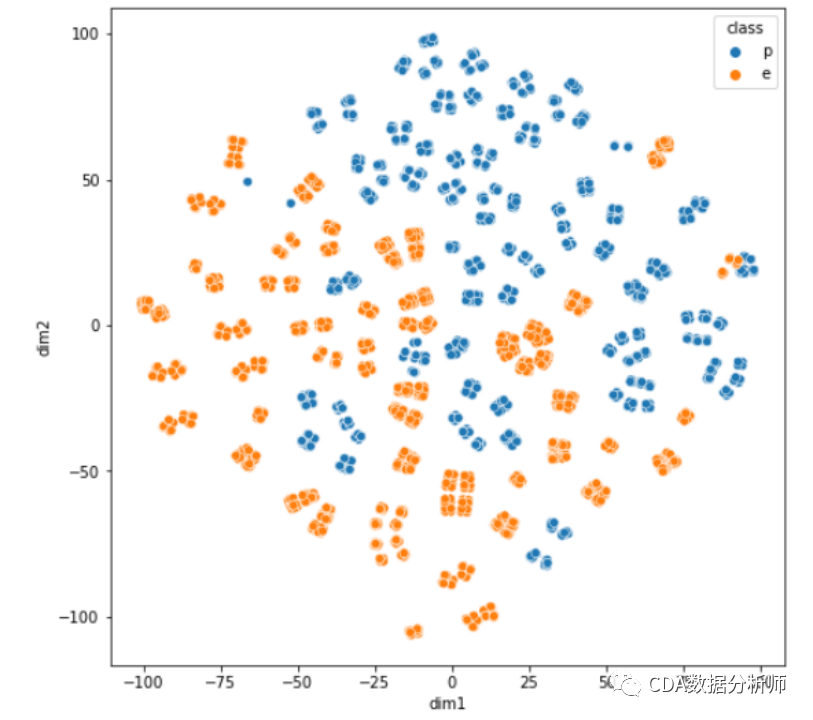

plt.show()

从可视化的结果可以看出，基于PCA降维的结果会产生重叠，这是因为主成分降维无法维护数据的局部结构而导致的，而基于t-SNE降维的结果分类更加清晰，基本没有类别之间的重叠，这就是t-SNE算法在降维过程中很好的保留了数据局部特征而产生的结果，所以，t-SNE算法可以很好的用来进行数据降维和可视化展示。