机器学习实战 | 支持向量机·sklearn 参数详解

接上篇的内容「一文带你了解什么是支持向量机」，相信大家已经对 SVM 已有些了解，关于 SVM 的公式推导可参考李航《统计学习方法》第七章，讲的非常清楚，这里我就不展开讲了。今天给大家带来的是 Sklearn 中的 SVM 参数介绍及简单应用。

先来回顾一些基本的概念：

线性/非线性
线性是指量与量之间按比例，成直线关系，在数学上可理解为一阶导数为常数的函数；而非线性是指不按比例，不成直线关系，一阶导数不为常数的函数。
线性可分/不可分
对于二分类问题，有那么一条直线可以把正负实例点完全分开，这些数据就是线性可分的；而线性不可分就是找不到一条直线可以把正负实例点完全分开。
超平面
其实就是实例点从二维空间转移到三维甚至多维空间中，这个时候不能再用直线划分，而需要用平面去划分数据集，这个平面就称为超平面。
支持向量
在线性可分的情况下，训练数据集的样本点与分离超平面距离最近的样本点称为支持向量，而支持向量机的目的就是求取距离这个点最远的分离超平面，这个点在确定分离超平面时起着决定性作用，所以把这种分类模型称为支持向量机。

sklearn 提供了很多模型供我们使用，包括以下几种：

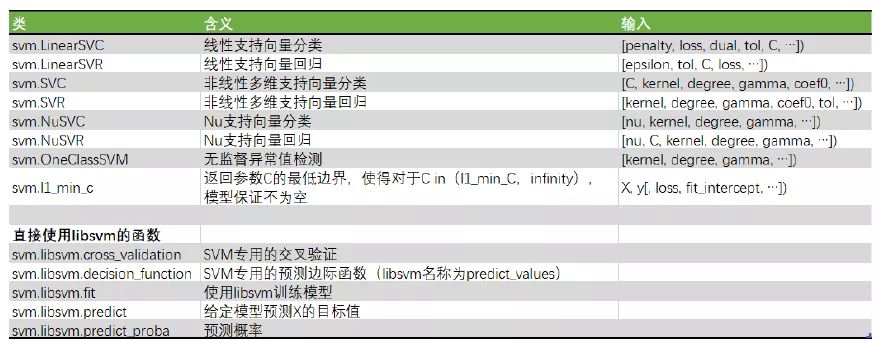
可以看到 SVM 在 sklearn 上有三个接口（这里我只介绍分类方法），分别是 LinearSVC、SVC 和 NuSVC。最常用的一般是 SVC 接口。除了特别表明是线性的两个类 LinearSVC 和 LinearSVR 之外，其他的所有类都是同时支持线性和非线性的。NuSVC 和 NuSVC 可以手动调节支持向量的数目，其他参数都与最常用的 SVC 和 SVR 一致。而 OneClassSVM 则是无监督的类。

SVC

SVC 的 sklearn 接口

class sklearn.svm.SVC(C=1.0, kernel=’rbf’, degree=3, gamma=’auto_deprecated’, coef0=0.0, shrinking=True, probability=False, tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1, decision_function_shape=’ovr’, random_state=None)

常用参数

C
错误项的惩罚参数C，浮点型，默认为 1.0，C越大，即对分错样本的惩罚程度越大，因此在训练样本中准确率越高，但是泛化能力降低，越容易产生过拟合。相反，减小C的话，容许训练样本中有一些误分类错误样本，泛化能力强。对于训练样本带有噪声的情况，一般采用后者，把训练样本集中错误分类的样本作为噪声。
kernel 核函数类型，字符串类型，默认为rbf。可选参数为：

`linear`：线性核函数
`poly`：多项式核函数
`rbf`：径像核函数/高斯核
`sigmod`：sigmod 核函数
`precomputed`：核矩阵。`precomputed`表示自己提前计算好核函数矩阵，这时候算法内部就不再用核函数去计算核矩阵，而是直接用你给的核矩阵，核矩阵需要为`n*n`。

probability
预测时是否使用概率估计，布尔型，默认为 False，这必须在调用fit()之前启用。

线性支持向量机 LinearSVC

线性支持向量机其实与 SVC 类中选择linear作为核函数的功能类似，但是其背后的实现库是 liblinear 而不是 libsvm，这使得在线性数据上，linearSVC 的运行速度比 SVC 中的linear核函数要快，不过两者的运行结果相似。在现实中，许多数据都是线性的，因此我们可以依赖计算得更快得 LinearSVC 类。除此之外，线性支持向量可以很容易地推广到大样本上，还可以支持稀疏矩阵，多分类中也支持 ovr 方案。

线性支持向量机的许多参数看起来和逻辑回归非常类似，比如可以选择正则化参数，可以选择损失函数等等，这也让它在线性数据上表现更加灵活。

LinearSVC 的 sklearn 接口

class sklearn.svm.LinearSVC(penalty='l2', loss='squared_hinge', dual=True, tol=0.0001, C=1.0, multi_class='ovr', fit_intercept=True, intercept_scaling=1, class_weight=None, verbose=0, random_state=None, max_iter=1000)

常用参数

penalty
正则化参数，有 L1 和 L2 两种参数可选，仅 LinearSVC 有。和逻辑回归中地正则惩罚项非常类似，L1 会让决策边界中部分特征的系数 w 被压缩到 0，而 L2 会让每个特征都被分配到一个不为 0 的系数。
loss
在求解决策边界过程中使用的损失函数，有hinge和squared_hinge两种可选，前者又称 L1 损失，后者称为 L2 损失，默认是是squared_hinge，其中hinge是 SVM 的标准损失，squared_hinge是hinge的平方。
dual
布尔型，默认是 True。选择让算法直接求解原始的拉格朗日函数，或者求解对偶函数。当选择为 True 的时候，表示求解对偶函数，如果样本量大于特征数目，建议求解原始拉格朗日函数，设定dual = False。

和 SVC 一样，LinearSVC 也有C这个惩罚参数，但 LinearSVC 在C变大时对C不太敏感，并且在某个阈值之后就不能再改善结果。

NuSVC

SVC 和 NuSVC 方法基本一致，唯一区别就是损失函数的度量方式不同（NuSVC 中的nu参数和 SVC 中的C参数）。

NuSVC 的 sklearn 接口

class sklearn.svm.NuSVC(nu=0.5, kernel='rbf', degree=3, gamma='auto', coef0=0.0, shrinking=True, probability=False, tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1, decision_function_shape='ovr', random_state=None))

常用参数

nu
训练误差部分的上限和支持向量部分的下限，取值在（0，1）之间，默认是0.5。

实战案例

数据及代码来自：https://github.com/626626cdllp/sklearn

import numpy as np
from sklearn import svm  # svm支持向量机
import matplotlib.pyplot as plt # 可视化绘图


    


data_set = np.loadtxt("SVM_data.txt")
train_data = data_set[:,0:2]   # 训练特征空间
train_target = np.sign(data_set[:,2])  # 训练集类标号

test_data = [[3,-1], [1,1], [7,-3], [9,0]] # 测试特征空间
test_target = [-1, -1, 1, 1]  # 测试集类标号

plt.scatter(data_set[:,0],data_set[:,1],c=data_set[:,2])  # 绘制可视化图
plt.show()

# 创建模型
clf = svm.SVC()
clf.fit(X=train_data, y=train_target,sample_weight=None)  # 训练模型。参数sample_weight为每个样本设置权重。应对非均衡问题
result = clf.predict(test_data)  # 使用模型预测值
print('预测结果：',result)  # 输出预测值[-1. -1.  1.  1.]

# 获得支持向量
print('支持向量：',clf.support_vectors_)



    
# 获得支持向量的索引
print('支持向量索引：',clf.support_)
# 为每一个类别获得支持向量的数量
print('支持向量数量：',clf.n_support_)


# # ===============================Linear SVM======================
from sklearn.svm import LinearSVC

clf = LinearSVC() # 创建线性可分svm模型，参数均使用默认值
clf.fit(train_data, train_target)  # 训练模型
result = clf.predict(test_data)  # 使用模型预测值
print('预测结果：',result)  # 输出预测值[-1. -1.  1.  1.]


# # ===============================Linear NuSVC======================
from sklearn.svm import NuSVC

clf = NuSVC() # 创建线性可分svm模型，参数均使用默认值
clf.fit(train_data, train_target)  # 训练模型
result = clf.predict(test_data)  # 使用模型预测值
print('预测结果：',result)  # 输出预测值[-1. -1.  1.  1.]