统计学是通过搜索、整理、分析、描述数据等手段,以达到推断所测对象的本质,甚至预测对象未来的一门综合性科学。
那什么是统计思维?
统计思维是透过现象看本质的过程,其中现象指的是数据本身,本质指的是数据背后的规律。简单来说,统计思维就是找规律的思维。
在上一篇文章中提到过,机器学习的核心是,让机器通过算法从现有数据中学习,然后对新数据做出预测。这里的学习,其实指的就是数据背后的规律,所以,统计思维也是机器学习的必备技能之一。
当然,这个规律怎么找是一个很大的学问,会用到大量的数学及其它学科的专业知识。但是,这并不意味着我们要先把所有的专业知识都学完之后,再去培养统计思维,而更好的一种选择是,在实践和解决问题的过程中,学习并掌握涉及到的理论和方法。
本文会利用Python中提供的强大工具,并配合实例讲解,教大家如何开始进行统计思考,有意识地培养统计思维。
【工具】Python 3
【数据】tushare.pro 、Datacamp
【注意】本文注重的是方法的讲解,请大家灵活掌握。
01
画图分析
画图始终是探索数据最直观的方法,在《最简洁的Python时间序列可视化实现》这篇文章中,已经向大家介绍过用Python中的matplotlib库画图的一些方法,本文会拓展更多新内容,并且再介绍一个非常好用的作图库Seaborn。
Seaborn是一个基于matplotlib的Python数据可视化库,能够便于我们作出各种炫酷的统计图形。
① 直方图
先从tushare.pro导入股票的前复权日线行情数据,并同时导入matplotlib
和seaborn库。调用plt.hist()画直方图,默认的bins参数值为10,效果如下:
import tushare as ts
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
ts.set_token('your token')
pro = ts.pro_api()
df = ts.pro_bar(ts_code='000001.SZ', adj='qfq', start_date='20190101', end_date='20190131')[['ts_code', 'trade_date', 'close']]
df.sort_values('trade_date', inplace=True)
df_close = np.array(df['close'])
print(df_close)
sns.set()
_ = plt.hist(df_close)
plt.xlabel('000001.SZ_close_price')
plt.ylabel('count')
plt.show()
将bins值设置为数据集大小的平方根,效果如下:
n_data = len(df_close)
n_bins = np.sqrt(n_data)
n_bins = int(n_bins)
print(n_bins)
_ = plt.hist(df_close, bins=n_bins)
plt.xlabel('000001.SZ_close_price')
plt.ylabel('count')
plt.show()
值得注意的是,画直方图有两个缺点:一个是,对于同一个数据集,参数bins的值不同,显示出来的图形效果也不同。另一个是,直方图并不会呈现数据的实际值。
② 蜂窝图
为了解决上面提到的这两个问题,我们可以画蜂窝图,先从tushare.pro导入由三只股票合并成的表格数据,然后调用swarmplot()函数画图,效果如下:
code_list = ['000001.SZ', '002142.SZ', '600000.SH']
df_all = pd.DataFrame()
for code in code_list:
print(code)
df = ts.pro_bar(ts_code=code, adj='qfq', start_date='20180101', end_date='20181231')[['trade_date', 'ts_code', 'close']]
df.sort_values('trade_date', inplace=True)
df_all = df_all.append(df, ignore_index=True)
print(df_all)
_ = sns.swarmplot(x='ts_code', y='close', data=df_all)
plt.show()
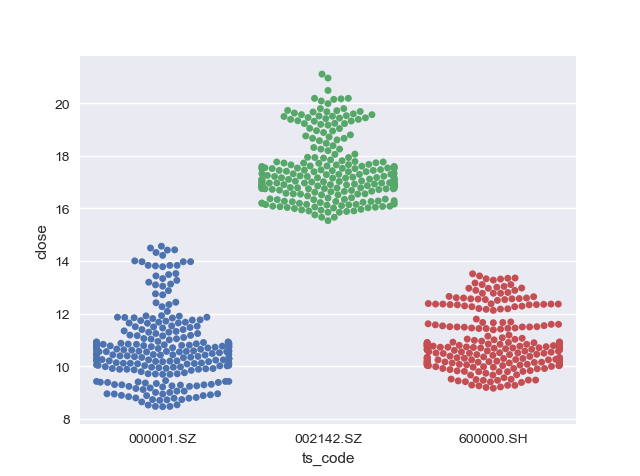
③ 经验累积分布函数图ECDF
蜂窝图的缺点是,虽然它显示出了数据集所有的实际数值,但我们并不能直观地看出这些数据的分布特征,因此经验累积分布函数图会是一个更好的选择。
经验累积分布函数ECDF是值到其在分布中百分位数的映射。假设ECDF是x的函数,其中x是分布中的某个值,计算给定x 的ECDF(x),就是计算样本中小于等于x 的值的概率。
我们可以自己定义一个函数来计算ECDF,先把数据从小到大排序,然后计算累积的概率。
def ecdf(data):
"""Compute ECDF for a one-dimensional array of measurements."""
n = len(data)
x = np.sort(data)
y = np.arange(1, len(data)+1) / n
return x, y
print(df_close)
x_vers, y_vers = ecdf(df_close)
_ = plt.plot(x_vers, y_vers, marker='.', linestyle='none')
_ = plt.xlabel('000001.SZ_close_price')
_ = plt.ylabel('count')
plt.show()
[ 9.19 9.28 9.75 9.74 9.66 9.94 10.1 10.2 10.11 10.24 10.48 10.25
10.43 10.34 10.28 10.35 10.52 11. 10.94 11. 10.95 11.1 ]
上图中画圈的点,就表示股价小于等于10.25的概率大约是0.5。
02
定量分析
除了最直观的画图,我们也可以通过计算统计值探索数据,最常见的有平均数、中位数、百分位数、方差、标准差等。
平均数、中位数、方差和标准差是大家比较熟悉的统计指标,这里就不作过多介绍了,直接附上代码,如下:
print(df_close)
[ 9.19 9.28 9.75 9.74 9.66 9.94 10.1 10.2 10.11 10.24 10.48 10.25
10.43 10.34 10.28 10.35 10.52 11. 10.94 11. 10.95 11.1 ]
print('mean:', np.mean(df_close))
print('median:', np.median(df_close))
print('variance:', np.var(df_close))
print('standard deviation:', np.std(df_close))
mean: 10.265909090909089
median: 10.265
variance: 0.2749423553719008
standard deviation: 0.5243494592081704
接下来,我们重点介绍一下百分位数percentile的概念。它的定义是,如果将一组数据从小到大排序,并计算相应的累计百分位,则某一百分位所对应数据的值就称为这一百分位的百分位数。
举个例子,假如你的某次考试成绩是90分,是第80百分位,那就说明你的成绩比80%的其他同学要好。
下面我们结合实例和箱型图来理解一下这个概念。如果要计算一组数据的分位数,可以直接调用np.percentile()【1】函数,如下:
a = np.array([1, 2, 3, 4, 5])
print(np.percentile(a, 50))
3.0
箱形图boxplot,是一种用作显示一组数据分散情况资料的统计图,如下所示。
下四分位数Q1 = 第25百分位数
中位数Q2 = 第50百分位数
上四分位数Q3 = 第75百分位数
上限 = Q3 + 1.5IQR
下限 = Q1 - 1.5IQR
四分位距IQR = Q3 − Q1
异常值 = 下限以下、上限以上的值
中位数Q2的确定比较简单,当数组个数为奇数时,就是处在中间位置的那个值,当个数为偶数时,就是处在中间位置的两个值的平均值。
与中位数不同的是,四分位数位置的确定方法有几种,每种方法得到的结果会有一定差异,但差异不会很大。
假设数组中有n个值,以n-1为基础的四分位数位置的确定方法如下,这也是np.percentile()函数所使用的方法:
Q1的位置 = 1+(n-1)x 0.25
Q3的位置 = 1+(n-1)x 0.75
a = np.array([10, 20, 30, 40])
n = len(a)
Q1_loc = 1 + np.multiply((n-1), 0.25)
Q3_loc = 1 + np.multiply((n-1), 0.75)
print(Q1_loc)
print(Q3_loc)
1.75
3.25
Q1 = np.percentile(a, 25)
Q3 = np.percentile(a, 75)
print(Q1)
print(Q3)
17.5
32.5
Q1 = 0.75 * 20 + 0.25 * 10 = 17.5
Q3 = 0.75 * 30 + 0.25 * 40 = 32.5
Q1和Q3是按照上面的公式计算的,原则就是先确定位置、再根据所在区间计算具体的值。
上例中的Q1_loc = 1.75,位置1.75在位置[1, 2]区间内,对应的数值区间为[10, 20],又因为1.75离2近,所以赋予20更高的权重0.75,赋予10更低的权重0.25。
同理,Q3_loc = 3.25,位置3.25在位置[3, 4]区间内,对应的数值区间为[30, 40],又因为3.25离3近,所以赋予30更高的权重0.75,赋予40更低的权重0.25。
注:上例中的权重0.75和0.25,根据n取值的不同会有变化,但原理是一样的,且和始终是1。
03
离散型随机变量
统计推断依赖于概率。概率反映的是随机事件出现的可能性,由于数据的产生本身就有一定随机性,我们很少能从数据中绝对肯定地说出任何有意义的东西,所以需要使用概率语言对数据进行定量陈述。
对于具有不同分布特征的数据集,求解概率的方法也不同,但整个模拟求解的过程基本上可以总结为:生成符合某一分布特征的随机数→进行大量重复的试验→得到估计量作为概率,这也是蒙特卡洛模拟的基本思想。
首先,结合实例介绍一下如何用numpy库中的random模块生成随机数。调用np.random.random()函数能够生成随机浮点数,取值范围为[0,1),每次调用的取值都有所不同。
print(np.random.random())
print(np.random.random())
0.8306703392370048
0.7909333011537936
我们可以把参数size设置为一个很大的数字,并作直方图看看效果,如果这些数字确实是随机产生的,那么直方图中每个区间的高度都应该接近相等的高度,如下所示。
random_numbers = np.random.random(size=100000)
_ = plt.hist(random_numbers)
plt.show()
下面,我们介绍一下常见的几个离散型随机变量的概率分布。
① 0-1分布,也叫伯努利一次试验。
0-1分布是只进行一次事件试验,该事件发生的概率为p,不发生的概率为1-p,比如典型的抛硬币。
② 二项分布,也叫n重伯努利试验。
二项分布指的是重复n次独立的伯努利试验。在每次试验中只有两种可能的结果,而且两种结果发生与否互相对立,并且相互独立,与其它各次试验结果无关,事件发生与否的概率在每一次独立试验中都保持不变,公式如下:
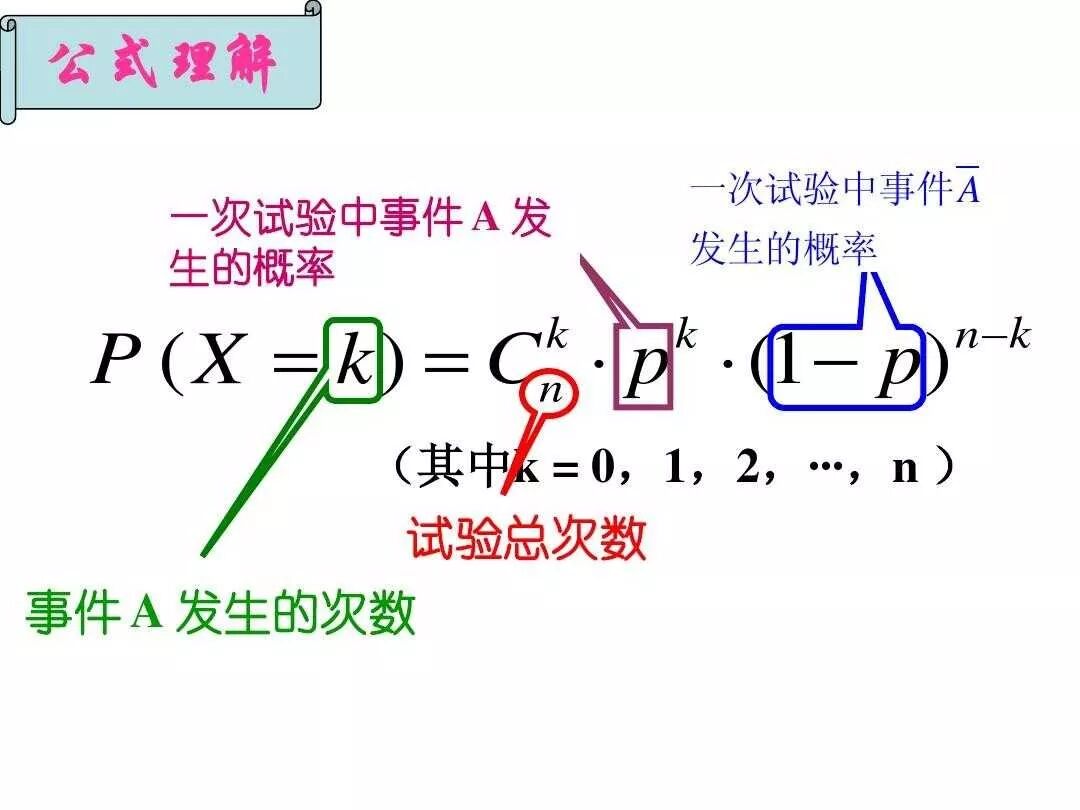
图片来自网络
我们可以调用np.random.binomial(n, p, size=None)【2】函数来模拟n重伯努利试验,其中参数n代表n次试验,p代表事件发生的概率,size代表一共进行了几次n重伯努利试验。
s = np.random.binomial(10, 0.5, 100)
print(s)
[5 9 2 2 7 3 4 7 6 5 7 7 5 5 3 6 6 6 5 7 6 7 6 3 7 6 5 6 5 6 3 7 8 7 4 4 4
5 7 3 8 3 2 3 6 2 7 5 6 2 3 5 5 5 7 5 4 7 4 5 3 3 8 4 5 4 4 4 7 3 3 8 7 3
5 4 6 4 3 5 5 6 7 8 2 6 6 6 3 6 7 5 5 3 5 4 6 5 8 4]
假设要求解每次试验抛10次硬币,试验100次,其中每次正好抛出5次正面的概率,则代码如下:
p = sum(s == 5) / 100
print(p)
0.26
累计分布函数图CDF如下:
x, y = ecdf(s)
_ = plt.plot(x, y, marker='.', linestyle='none')
_ = plt.ylabel('CDF')
plt.show()
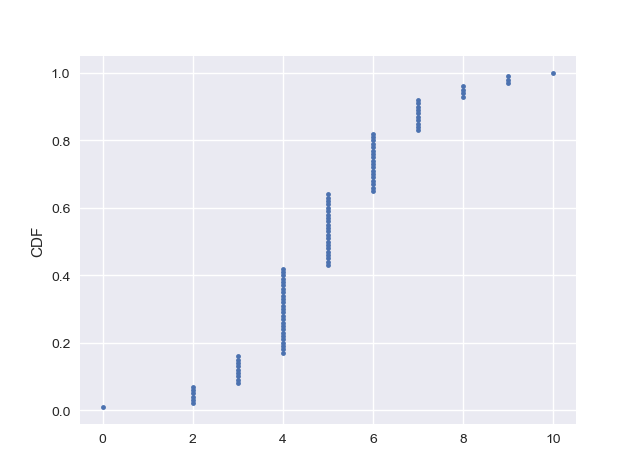
③ 泊松分布
泊松分布是指某时间段、某场合下、源源不断地质点来流的个数。比如,一小时内某个网站的点击量,每天晚上7-9点,到某个商场购物的顾客人数等等,公式如下。
其中,参数λ是单位时间(或单位面积)内随机事件的平均发生次数,同样,我们可以调用numpy.random.poisson(lam=1.0, size=None)【3】函数实现对泊松分布的模拟。
s = np.random.poisson(5, 100)
print(s)
[ 3 6 4 7 5 4 7 7 7 5 6 3 0 4 2 2 4 4 5 4 4 5 4 4
4 6 10 2 9 5 5 3 5 5 5 6 7 7 5 10 2 7 7 3 5 4 7 6
1 4 10 4 4 6 6 9 4 9 6 8 6 4 8 7 3 4 3 5 4 3 7 4
5 4 6 4 1 3 1 5 5 5 4 1 7 5 8 1 7 1 4 2 3 4 7 3
8 4 6 3]
假设要求解100次试验中,每次试验的结果大于5的概率,则代码如下:
p = sum(s > 5) / 100
print(p)
0.35
04
连续型随机变量
连续型随机变量是指如果随机变量的所有可能取值不可以逐个列举出来,而是取数轴上某一区间内的任一点的随机变量。
① 正态分布
正态分布是具有两个参数μ和σ^2的连续型随机变量的分布,第一参数μ是遵从正态分布的随机变量的均值,第二个参数σ^2是此随机变量的方差,所以正态分布记作N(μ,σ^2 )。
遵从正态分布的随机变量的概率规律为取μ邻近的值的概率大 ,而取离μ越远的值的概率越小;σ越小,分布越集中在μ附近,σ越大,分布越分散。
特别地,当均值μ=0,标准差σ=1时,正态分布就成为标准正态分布,记为N(0, 1)。
我们可以调用np.random.normal(loc=0.0, scale=1.0, size=None)【4】函数来模拟正态分布,其中参数loc代表均值,参数scale代表标准差。
下面,通过画概率密度函数图PDF和累计分布函数图CDF,看一下对于不同的均值和标准差,它们的图形会有怎样的变化。
samples_std1 = np.random.normal(20, 1, size=100000)
samples_std3 = np.random.normal(20, 3, size=100000)
samples_std10 = np.random.normal(20, 10, size=100000)
_ = plt.hist(samples_std1, bins=100, density=True, histtype='step')
_ = plt.hist(samples_std3, bins=100, density=True, histtype='step')
_ = plt.hist(samples_std10, bins=100, density=True, histtype='step')
_ = plt.legend(('std = 1', 'std = 3', 'std = 10'))
plt.ylim(-0.01, 0.42)
plt.show()
x_std1, y_std1 = ecdf(samples_std1)
x_std3, y_std3 = ecdf(samples_std3)
x_std10, y_std10 = ecdf(samples_std10)
_ = plt.plot(x_std1, y_std1, marker='.', linestyle='none')
_ = plt.plot(x_std3, y_std3, marker='.', linestyle='none')
_ = plt.plot(x_std10, y_std10, marker='.', linestyle='none')
_ = plt.legend(('std = 1', 'std = 3', 'std = 10'), loc='lower right')
plt.show()
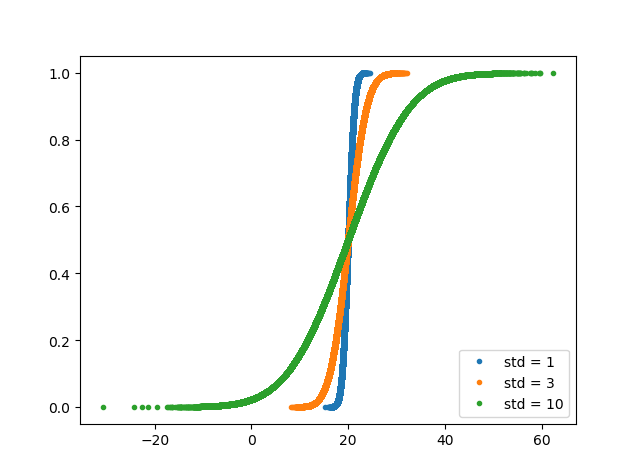
samples_mean1 = np.random.normal(0, 1, size=100000)
samples_mean3 = np.random.normal(3, 1, size=100000)
samples_mean10 = np.random.normal(10, 1, size=100000)
_ = plt.hist(samples_mean1, bins=100, density=True, histtype='step')
_ = plt.hist(samples_mean3, bins=100, density=True, histtype='step')
_ = plt.hist(samples_mean10, bins=100, density=True, histtype='step')
_ = plt.legend(('mean = 0', 'mean = 3', 'mean = 10'))
plt.ylim(-0.01, 0.42)
plt.show()
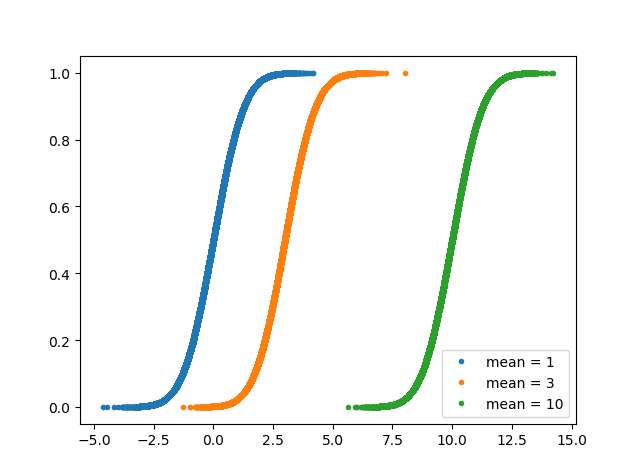
x_mean1, y_mean1 = ecdf(samples_mean1)
x_mean3, y_mean3 = ecdf(samples_mean3)
x_mean10, y_mean10 = ecdf(samples_mean10)
_ = plt.plot(x_mean1, y_mean1, marker='.', linestyle='none')
_ = plt.plot(x_mean3, y_mean3, marker='.', linestyle='none')
_ = plt.plot(x_mean10, y_mean10, marker='.', linestyle='none')
_ = plt.legend(('mean = 1', 'mean = 3', 'mean = 10'), loc='lower right')
plt.show()
假设要计算样本中值小于等于1个标准差的概率,方法如下:
samples = np.random.normal(0, 1, size=1000000)
print(samples)
prob = np.sum(samples <= 1) / len(samples)
print('Probability:', prob)
[-1.15137588 2.13435251 -0.23445714 ... -0.41228481 -0.48010039
0.65948965]
Probability: 0.840984
概率理论和统计学中,指数分布是描述泊松分布过程中的事件之间的时间的概率分布,即事件以恒定平均速率连续且独立地发生的过程。
指数分布可以用来表示独立随机事件发生的时间间隔,比如旅客进机场的时间间隔、中文维基百科新条目出现的时间间隔等等。
指数分布的一个重要特征是无记忆性。这表示如果一个随机变量呈指数分布,当s, t>0时,
P(T>t+s|T>t) = P(T>s)
举个例子,守株待兔的故事相信大家都听说过,假设A在树下等了t个小时,没有遇到兔子,这个时候B来了,两个人一起等,他们再等待s个小时遇见兔子撞树的概率是一样的,这就是上面所说的“无记忆性”。
我们可以调用np.random.exponential(scale=1.0, size=None)【5】函数来模拟指数分布,其中参数scale=1/λ,可以理解为平均等待时间。
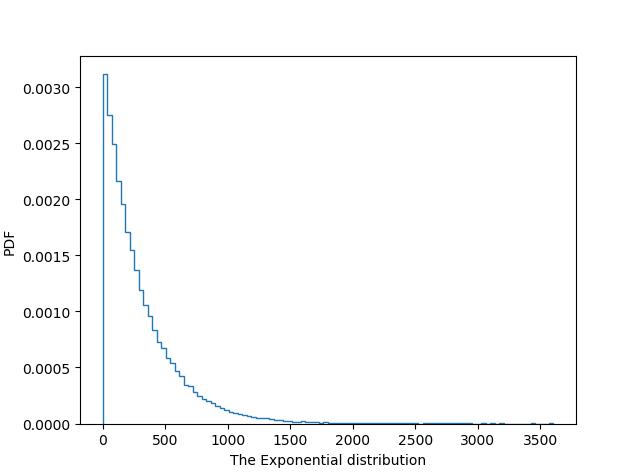
a = np.random.exponential(300, size=100000)
_ = plt.hist(a, bins=100, density=True, histtype='step')
_ = plt.xlabel('The Exponential distribution')
_ = plt.ylabel('PDF')
plt.show()
x, y = ecdf(a)
_ = plt.plot(x, y, marker='.', linestyle='none')
_ = plt.xlabel('The Exponential distribution')
_ = plt.ylabel('CDF')
plt.show()
https://docs.scipy.org/doc/numpy-1.15.1/reference/generated/numpy.random.binomial.html?highlight=random%20binomial#numpy.random.binomial【2】
https://docs.scipy.org/doc/numpy-1.15.1/reference/generated/numpy.random.poisson.html?highlight=numpy%20random%20poisson#numpy.random.poisson【3】
https://docs.scipy.org/doc/numpy-1.15.0/reference/generated/numpy.random.normal.html【4】
https://docs.scipy.org/doc/numpy-1.13.0/reference/generated/numpy.random.exponential.html【5】