
作者:韦子扬,懂点代码。wzy-codify.com
Blog: zhuanlan.zhihu.com/p/85518062
引言:
给定一个长度为n的无序数组,再给你任意一个数字k,请找出这个数组中和k最近的m个数(这个k可以不出现在这个数组中)
题目其实很简单,想了一会儿给出了一个方案如下:
我的思路
首先开辟一个新的数组D1,代表这个数组与k的距离,用求绝对值的方式来把距离求出来(第一个元素是距离,第二个元素是本身),然后再进行快排,然后取D1中前m个元素即可,代码实现如下:
if __name__ == "__main__":
n = 15
k = 5
m = 5
li = [1,5,3,2,6,7,1,4]
print(
def solution1(li, k, m):
new_li = [(abs(each - k),each
) for each in li]
new_li.sort(key=lambda a: a[0])
return [each[1] for each in new_li[:m]]
result = solution1(li, k, m)
print(result)
可以想到这个算法的复杂度是n+nlogn,这个方法可以是可以,但明显不是最好的解决方法,几经面试官提示后,由于之前只是看人用过,但没有系统地学过 堆,最后没有想到用堆来解决这个问题,知耻后勇吧,回去以后立刻仔细看了一遍这个方面的知识。
堆是什么
堆是一种完全二叉树,复习一下完全二叉树的定义,完全二叉树的形式是指除了最后一层之外,其他所有层的结点都是满的,而最后一层的所有结点都靠左边。教材上定义如下:
若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。
如下图所示,就是一种典型的完全二叉树:
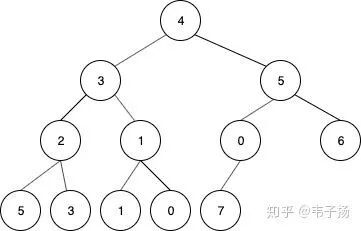
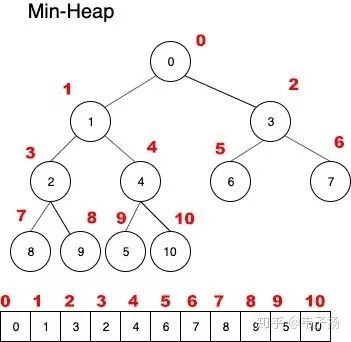
而最小堆要求,对于任意一个父结点来说,其子结点的值都大于这个父节点,同理,最大堆就是说,其子节点的值都小于这个父节点。很显然上图不是一个最小堆,下图才是:
堆的实现
之前说到,堆是一种完全二叉树,但是否就意味着我们真的要用树来表示它呢?答案是否定的,因为完全二叉树有其非常卓越的性质:对于任意一个父节点的序号n来说(这里n从0算),它的子节点的序号一定是2n+1,2n+2,因此我们可以直接用数组来表示一个堆。所以对于上图来说,我们可以用[0,1,3,2,4,6,7,8,9,5,10]来表示这个堆。
另外,对堆的所有操作都一定要保持操作完以后,他仍然是个堆,基于这个原则,我们来实现堆的操作。我们如下初始化一个堆:
class Heap(object):
def
__init__(self, array):
self.array = array
def __str__(self):
return str(self.array)
def __len__(self):
return len(self.array)
1.插入Insert(push)
下面我画了一个示意图,当一个新元素想要插入这个堆的时候,我们首先把他放到这个堆的末尾。然后依据堆的特性,对它的位置进行调整,由于要保持父结点的值要永远少于其子节点的值,而2的直接父节点6大于了它,所以要把他们两的位置对换,对换完毕后,再检查这个堆的状态,发现其父节点3仍然大于自己,所以继续往上和3对换,结束后,和0比较,0不大于自己,所以停留在原地不动,插入结束。
简单来说,插入一个结点就是将该元素插入到堆的尾部,然后不断上浮调整位置,直至满足堆的条件。
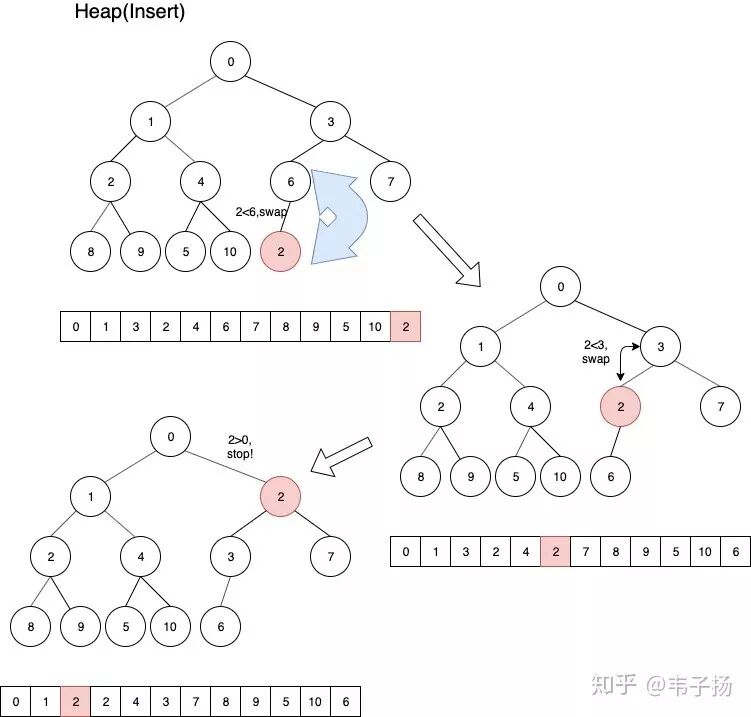
代码实现如下,push的话参数index都是len(self.array)
def insert(self, num, index):
self.array.append(num)
parent_index = index
while parent_index >= 0 and self.array[parent_index] > num:
self.array[parent_index], self
.array[index] = self.array[index], self.array[parent_index]
if parent_index == 0:
break
index = parent_index
parent_index = parent_index
2.删除pop
如下图所示,删除一般指的都是删除堆顶元素,在堆顶元素被拿掉后,将末尾元素置换上来,然后进行下沉操作,由于这是最小堆,堆顶一定是最小元素,首先6大于左结点1,需要下沉, 下沉完以后继续和它子节点比较,发现左结点2小于自身,继续下沉,最后8 和 9都比6大,停止下沉。总结来说,意思就是删除堆顶元素后,用末尾元素补上,然后不断下沉,直至满足堆的条件。
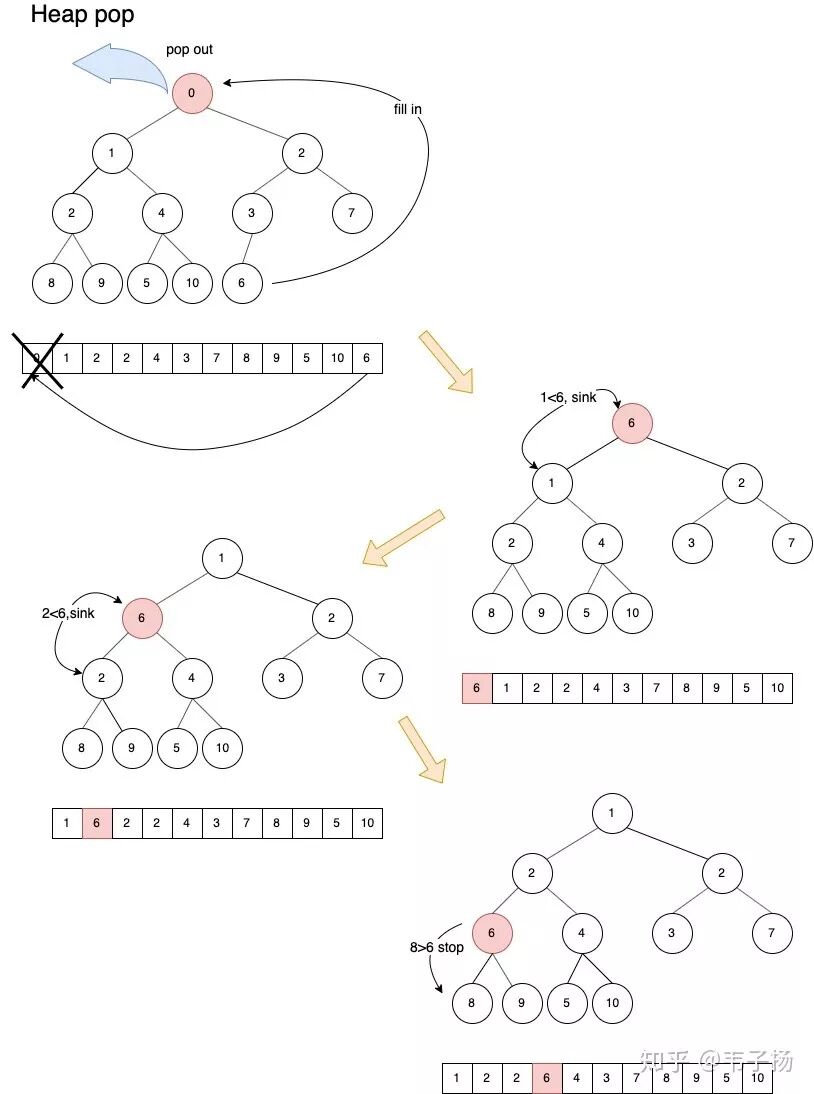
代码如下,首先要定义sink方法,然后在此基础上实现pop:
def sink(self, index, array):
left_node_index = index * 2 + 1
right_node_index = index * 2 + 2
if left_node_index array):
left_v = array[left_node_index]
if right_node_index >= len(array):
min_value = left_v
min_index = left_node_index
else:
right_v = array[right_node_index]
if left_v min_value = left_v
min_index = left_node_index
else:
min_value = right_v
min_index = right_node_index
if array[index] > min_value:
array[index], array[min_index] = array[min_index], array[index]
self.sink(min_index, array)
self.array[:len(array)] = array
def pop(self):
end_v = self.array.pop()
min_value = self.array[0]
self.array[0] = end_v
self.sink(0, self.array)
return min_value
3. 建堆
建堆的过程也非常简单,将每个父节点都进行下沉操作,即可完成建堆。所以我们的Heap类就可以变成:
def __init__(self, array):
self.array = array
for
index in range(len(array)
self.sink(index, self.array)
使用堆的思路
上面已经说完了堆的基本操作,下面讲一下堆是如何联系到这题的,简单来说,如果用堆,我们可以直接维持一个长度为m的最大堆,然后对这个长度为n的列表li进行遍历,每次遍历都把这个元素以及这个元素与k的距离组成的元祖塞到这个堆里去,当这个堆的长度大于m时,即pop出最大的元素(距离最远的元素),也就是说这个最大堆保留的永远都是与k最近的m个元素。由于删除与插入的复杂度都是logm,所以最终这个算法的复杂度是nlogm。注意由于m是肯定是小于n的,所以这个算法肯定比之前排序算法快,完整代码如下:
class MaxHeap(object):
def __init__(self, array):
self.array = array
for index in range(len(array)//2-1, -1, -1):
self.sink(index, self.array)
def sink(self, index, array):
left_node_index = index * 2 + 1
right_node_index = index * 2 + 2
if left_node_index left_v = array[left_node_index]
if right_node_index >= len(array):
max_value = left_v
max_index = left_node_index
else:
right_v = array[right_node_index]
if left_v[0] > right_v[0]:
max_value = left_v
max_index = left_node_index
else:
max_value = right_v
max_index = right_node_index
if array[index] array[index], array[max_index] = array[max_index], array[index]
self.sink(max_index, array)
self.array[:len(array)] = array
def insert(self, num, index):
self.array.append(num)
parent_index = index // 2
while parent_index >= 0 and self.array[parent_index][0] 0]:
self.array[parent_index], self.array[index] = self.array[index], self.array[parent_index]
if parent_index == 0:
break
index = parent_index
parent_index = parent_index // 2
def push(self, num):
self.insert(num, len(self.array))
def delete(self):
end_v = self.array.pop()
self.array[0] = end_v
self.sink(0, self.array)
def sort(self):
for index in
range(len(self.array)-1, 0, -1):
self.array[0], self.array[index] = self.array[index], self.array[0]
self.sink(0, self.array[:index])
def __str__(self):
return str(self.array)
def __len__(self):
return len(self.array)
if __name__ == "__main__":
n = 15
k = 5
m = 5
li = [1,5,3,2,6,7,1,4]
print('The elements in the list:', li)
def solution2(li, k, m):
max_heap = MaxHeap([])
for num in li:
dis = abs(num-k)
max_heap.push((dis, num))
if len(max_heap) > m:
max_heap.delete()
return [each[1] for each in max_heap.array]
result = solution2(li, k, m)
print(result)
堆的其他应用
看完堆以后,突然发现以前其实用过堆,只是当时调用的是Python优先级队列PriorityQueue那个库,而优先级队列的实现就是用堆来实现的,而优先级队列是A搜索的基础(所以以后做作业还是少调现成的库,不然A搜索实现完连它底层是堆都不知道)。
除此之外,堆还可以用来作为排序,思路是每次都把堆顶的元素和堆尾的元素交换,然后把除了堆尾的那个元素组成的堆进行堆化(就是把堆顶的元素进行下沉),不断重复直至堆为空为止。实现代码如下:
def sort(self):
for index in range(len(self.array)-1, 0, -1):
self.array[0], self.array[index] = self.array[index], self.array[0]
self.sink(0, self.array[:index])

阿里云双十一活动来袭
长按扫描下方二维码
即享云服务器新用户1折起购
最低86元/年,一起拼团更优惠!
↓ ↓ 长按扫码了解更多 ↓ ↓

【Python中文社区专属拼团码】
活动时间:2019年10月24日至2019年11月11日
活动对象:阿里云新用户,同一用户限购1单。
▼ 点击阅读原文,即享阿里云产品新用户1折优惠