“空间”，是全书知识介绍的概念主轴。矩阵所扮演的角色就是完成向量在不同空间之间的映射过程，理解了这一点就能把控住了整个线性代数的灵魂所在。那么，本章就将具体讨论不同形态的矩阵所对应的不同映射过程，并在此基础上探讨逆映射、逆矩阵存在的条件。
为夯实本章甚至全书的理论基础，我们还将专门安排一节的内容讨论向量空间和其中最重要的四个子空间。最后会从空间的角度出发，谈谈线性方程组的解这个实际应用问题，目的就是为了理解好空间这个核心概念。
本章主要涉及到的知识点有：
◇ 介绍列空间、零空间、行空间、左零空间这四个重要的子空间在上一章的内容中，我们学习到矩阵与向量的乘法会使得向量的空间位置甚至其所在空间的维度和形态都发生变化。那么，映射前的原始空间和映射后的目标空间之间存在着什么样的对应关系？这种对应关系的决定因素是什么？这将是我们这一小节要重点分析讨论的问题。
我们将从矩阵的形状-----这个看上去最为明显的特征入手进行分析。我们会发现“矮胖”形态的矩阵和“高瘦”形态的矩阵对应了不同的空间映射关系，即使是方阵与方阵之间，也存在着多种不同的映射情况。基于这些不同的观察现象，我们最终将引出“秩”-----这个映射后空间形态的决定因素，并挖掘他包含的几何意义，还将演示如何利用Python语言工具去求解一个具体矩阵的秩。
回顾上一章，在默认基底
所构成的
空间中，矩阵A与列向量x的乘法：Ax，其本质就是变换原始向量的基底。将默认基底中的各个基向量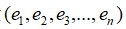
分别对应的变换为矩阵A的各个列，由矩阵A的各列充当目标向量新的“基向量”，再结合原始向量的坐标，最终得到目标向量在目标空间中的新位置。
因此我们可以概况的说：由于矩阵乘法的作用，原始向量的空间位置甚至其所在空间的维度和形态都发生了改变，这便是矩阵乘法的空间映射作用。
我们要再次着重强调一下：在第一段中我们将基向量这个词打了一个引号，原因是因为这种说法并不完全准确，没有考虑到很多特殊的情况。因为我们在上一章的结尾曾经提到过：矩阵A的各个列向量作为原始向量x默认基底经过转换后得到的目标向量，由于其在维度和线性相关性方面存在着多种不同的情况，因此这组目标向量的张成空间和原始向量所在的空间之间，就会存在着多种不同的对应关系。
本节我们将围绕下面这个乘法式子，来重点讨论这个问题。
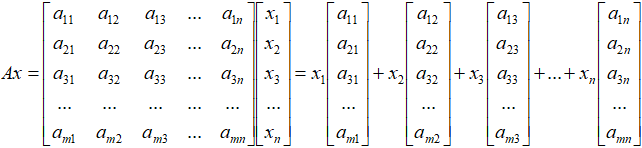
对于m行n列的矩阵A，当m
中的一个n维向量，向量x的n个默认基向量
分别被矩阵A映射成了n个m维的目标向量。
由于m
中的任意向量x经过映射作用后，都被转换到了一个维数更低的新空间之中，位于新空间中的新位置上。
由此，我们可以这么说：在满足m
。
说了这么多，可能还不是很直观。我们用一个2×3的实际矩阵A来举例：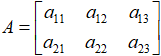
，映射前的原始列向量
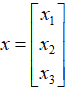是。我们知道，原始向量x是
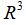空间中的一个三维向量，他所采用的是一组默认的基底：
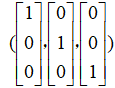，向量x就是基底的任意线性组合中的具体一种。
依照我们介绍的基变换思想，经过矩阵A的基变换后，这组默认的基底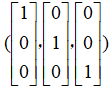
就被映射到了三个新的目标向量：
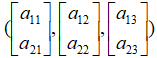，而映射后的目标向量就相应的变成了：
。
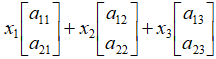映射前的列向量x，由于他的三个成分
可以取到任意值，因此向量x的分布即为整个
空间。那么我们关心的就是映射后的目标向量：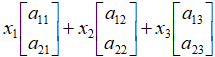
的整体分布情况，换句话说，这就是我们所说的映射后的空间。
这就回到了前面提到过的张成空间的问题，3个二维向量必然是线性相关的，但是仍然分为两种情况。
现在我们来看看另一种形态的矩阵，即m×n矩阵中的m>n这种情况，对应的我们称之为“高瘦”矩阵。
x的n个基向量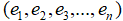
分别被矩阵A映射成了n个m维目标向量。由于m>n，从表面数值看上去，x映射后的目标向量的维数提高了，由n维变成了m维。那我们能不能说：经过矩阵A的映射作用，由原始向量x所构成的空间
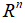变成了维数更高的空间
呢？
很显然，答案是否定的。哲学点来讲：一个事物想无中生有，那是不可能的。一个向量所携带的信息怎么能够平白无故的增加呢？
当然，这样说大家可能会觉得有点玄乎，我们来举一个实际的例子，比如说有一个形状为3×2的矩阵A：
。映射前的原始向量是二维空间
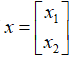中的，映射的过程则可以被表示为：
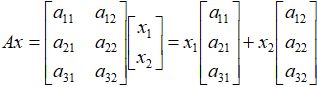，通过这个式子的计算，我们得到了最终的映射结果。
由于映射前的向量x是二维空间
中的任意一个向量，类比上一个章节，和可以取任意数，因此在矩阵A的乘法作用下，整个二维空间的映射结果就是目标向量
和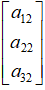
所张成的空间。
是不是同样感觉到非常熟悉？对，此时又回到老问题上来了，我们对于目标向量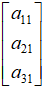
和
，同样是分成两种不同的情况进行讨论。
至于说如果矩阵A是一个n阶方阵，这种特殊情况下的结果是不是要稍微简单一些呢？就此我们来分析一下。分析方法也是相同的，核心问题仍然是分析矩阵A各个列的线性相关性。我们很容易发现，
空间中的向量经过矩阵A的映射，其目标空间的维度就是这n个n维列向量所张成空间的维度，其映射后得到的空间的维度必然小于等于n，当且仅当这n个列线性无关时可以取得到等号。
我们简单的用一个3阶方阵A来举例：
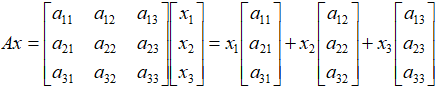
当矩阵A的三个列线性无关的时候，意味着原始向量x的基向量经过映射后得到的目标向量仍然可以构成三维空间
中的一组基。
这是非常好的一种情况，意味着原始空间
经过矩阵A的映射，其映射后得到的空间仍然是等维的三维空间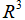。原始向量空间在这个过程中没有被压缩，并且映射后的目标空间内的每一个向量也都能找到其对应的原始空间中的向量。
这种一一映射的关系我们在后面讲到逆映射、逆矩阵的时候还会反复进行讨论的，这里先有一个整体印象就好。
老规矩，我们举实际的例子来看看：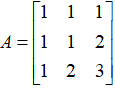
矩阵，原始向量 
，
，
。
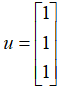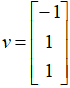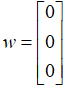向量u映射后的得到的结果为：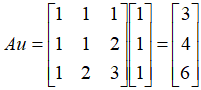
，向量v映射后的结果同理为：，零向量w经过映射后得到的结果仍然是目标空间中的零向量，如图2.5所示。
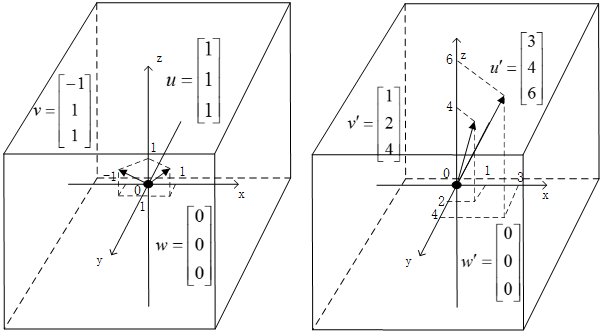
图2.5 列向量线性无关的矩阵进行的空间映射
而当矩阵A的三个列线性相关的时候，映射的过程其实就退化成了“高瘦”矩阵所对应的情况，由于之前详细用图分析过具体情形，我们这里就只需要简单的说明结论，相信大家对此是很容易理解的。
情况一：
当矩阵A的三个列共面但不共线的时候，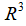
空间中的向量经过矩阵A的映射作用，最后都会分布在穿过原点，并“斜搭”在三维空间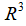中的一个平面上。
情况二：
当这三个列向量共线的时候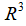，空间中的向量经过映射，最后都会分布在穿过原点并“斜穿”过三维空间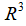中的一条直线上。
看到这些，你会觉得这些都是非常熟悉的场景了吧。
在这一节里，我们举了这么多的例子，画了这么多的图，是时候来总结、提炼一些规律性的东西了。我们把一个空间经过矩阵映射后得到的新空间称之为他的像空间。我们发现了一些有意思的现象：一个原始空间，被几个行数、列数分别相同的不同矩阵进行映射，最终得到的像空间的维数可能会是不同的；而被几个不同形状的矩阵分别进行映射，又有可能得到维数相同的像空间。
那么问题就来了，这里面所提到的像空间维度的决定因素是什么？
很明显，决定因素就是空间映射矩阵各列的线性相关性，由各列所张成的空间维数就是原始空间映射后的像空间维数。我们给由矩阵各列所张成空间的维数取了一个名字，就叫作这个映射矩阵的秩。其实从另一方面来看，秩也可以说成是该矩阵线性无关的列的个数，这两个说法相互之间是等价的。
我们不能道理懂了这么多，却依然不会动手。因此，在本节的最后我们来动手解决一下实际的问题，如何用Python工具来求解一个矩阵的秩？
我们一边回顾这一节中出现的5个典型矩阵，一边依据定义来求取他们的秩。
矩阵1：
，由矩阵
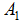的3个列所张成的空间维数是2，因此，矩阵的秩是2；
矩阵2：
，由矩阵
的3个列所张成的空间维数是1，因此，矩阵的秩是1；
矩阵3：
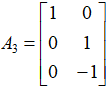，由矩阵
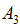的2个列所张成的空间维数是2，因此，矩阵的秩是2；
矩阵4：
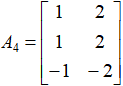，由矩阵
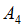的2个列所张成的空间维数是1，因此，矩阵的秩是1；
矩阵5：
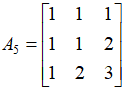，由矩阵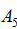
的3个列所张成的空间维数是3，因此，矩阵的秩是3。
我们用Python工具对他们进行一一验证。
代码如下：
import numpy as np
A_1 = np.array([[1, 1, 0],
[1, 0, 1]])
A_2 = np.array([[1, 2, -1],
[2, 4, -2]])
A_3 = np.array([[1, 0],
[0, 1],
[0, -1]])
A_4 = np.array([[1, 2],
[1, 2],
[-1, -2]])
A_5 = np.array([[1, 1, 1],
[1, 1, 2],
[1, 2, 3]])
print(np.linalg.matrix_rank(A_1))
print(np.linalg.matrix_rank(A_2))
print(np.linalg.matrix_rank(A_3))
print(np.linalg.matrix_rank(A_4))
print(np.linalg.matrix_rank(A_5))
运行结果：
经过上面的验证可以看出，程序运行得到的结果和我们的分析情况是一致的。在这一小节里，我们通过大量细致的举例，展现了空间在不同秩的矩阵映射作用下所得到的不同形态，并分析了各种不同形态背后的决定性因素：矩阵中线性无关的列的个数。这部分的基础知识和思维方式非常重要，建立好了这个概念将非常有助于我们加深对逆矩阵、线性方程组和投影相关内容的深刻理解。
本书所涉及的源代码已上传到百度网盘，供读者下载。请读者关注封底“博雅读书社”微信公众号，找到“资源下载”栏目，根据提示获取。
如果您对本书感兴趣，请进入当当网选购！
