Python部落(python.freelycode.com)组织翻译，禁止转载，欢迎转发。

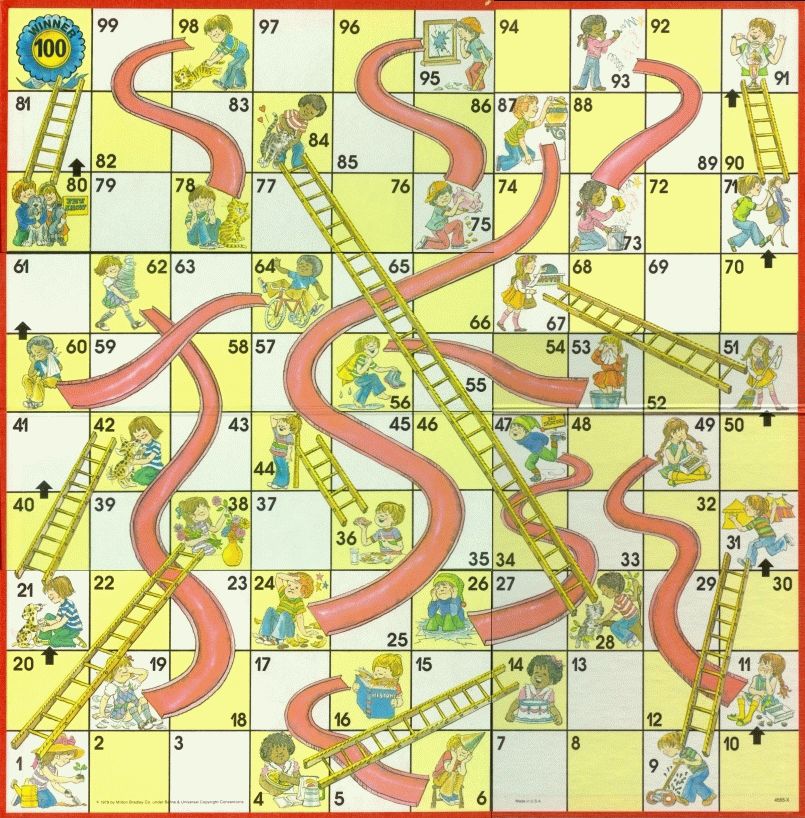
这周末我和我 4 岁大的女儿玩“梯子与滑梯”游戏玩的不亦乐乎。如果你没有玩过这个游戏，在此处我跟你稍微普及一下，这是一款经典的孩童棋盘游戏，在游戏中共计有 100 个格子，玩家们通过投掷骰子来决定如何走，梯子可以让你直接跳至相应的格子，滑梯则会让你退回相应的格子。也许你可以将这款游戏理解为一个可视化的随机过程。很刺激有没有？但是，其中也蕴含着一定的计算能力，同时，我们需要学会如何去完美的赢得游戏，顺便培养一下作为竞技爱好者的必备技能，所以我就自己一个人玩了玩这个游戏。

在那天上午的大概第二十三场游戏里，我发现我自己似乎掉进了一个无休无止的循环里，凭借梯子爬升，然后又使用滑梯回到原位，就这样没法结束这场游戏，于是乎我就在想这个游戏它能持续多久呢？一场游戏的平均时长是多少呢？游戏时长的数学分布的方差是多少呢？如何使用 Python 来简洁的解决这个问题呢？然后就在某一瞬间，我幡然领悟：这款游戏是一个无记忆的过程，也就是说，你怎么走只取决与你目前的位置，和你之前都做了什么没关系，所以我们可以使用马尔科夫随机过程来对其建模。也就是在我灵光一闪的那一刻，我终于走到了终点，此时我的脑海里已经基本上知道这篇博文该写些什么了。

当我将我的这个想法发在推特上后，其他人也指出了很多跟我想法相似的处理方法，所以我不敢保证我的想法是独一无二的。你可以将这片文章视为博客版的“老爸笑话”：我的主要目标不是创意，而是自娱自乐，如果有人觉得有趣，那便是额外的奖励。

直接模拟

对付这种动态游戏最直接的方法就是暴力模拟，也就是说，如果我们模拟足够多场游戏，我就可以得到游戏时间长度的一个数学分布，这个就近似于真实的分布。第一步就是需要仔细查看游戏棋盘，对这些这些网格上的梯子和滑梯的位置进行编码。

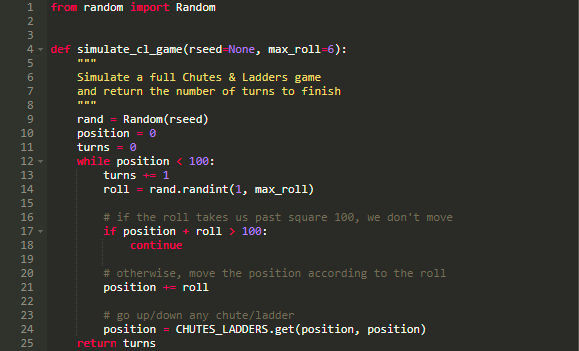
我们使用 Python 里的字典来存储这些位置信息：

完成这项工作之后，我们就可以使用下面的几行代码来进行模拟了。

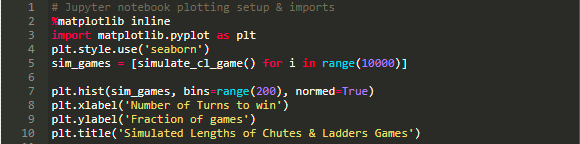
我们简单的调用一下这个函数，可以得到完成这个游戏需要多少步：

如果我们进行多次模拟，得到的结果就是完成这个游戏需要步数的一个数学分布。

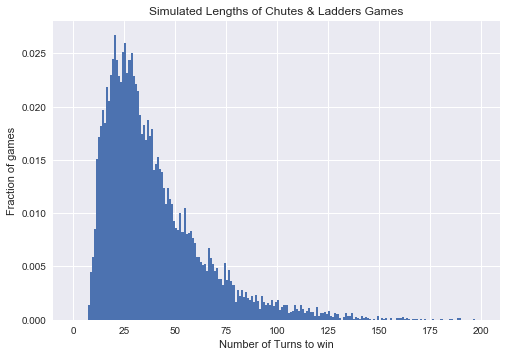
上图可以让我们得到一点东西，但是问题是上图只是游戏步数真实分布的一个近似，为了得到更加准确的结果，我们必然需要进行很多次模拟实验，这个就会在计算上花费大量的时间，计算成本过高。

幸好，我们还有另一种办法。

使用 马尔科夫过程 对此游戏建模

与暴力破解不同，我们可以同统计学的角度来考虑这个游戏。在某一步的时候，我们有六种等概率的选择，对应你掷骰子得到的 1,2,3,4,5,6。 只要你出发的位置确定了，这 6 个选择的结果就是确定的（结果指的是你下一步走到什么地方）。例如，在第一步时，我们可能的结果是 [38,2,3,14,5,6]，这六种结果是等概率出现的。我们可以使用一个长度为 101 的向量来对这些可能结果进行编码，向量列表中，索引为可能的结果，索引对应的值为这个结果的概率。其中 0 索引代表了起始位置，默认值为零。

此向量中的，每一个元素代表了从零位置到其对应索引位置的概率。上面这个向量就完全可以表示第一步的结果。依次类推，我们可以得到起始位置为 2 时，所对应的概率向量。

 同样的道理，这个向量描述了从第二个方格出发的所有游戏结果。

这样做的关键在于， 梯子与滑梯游戏是无记忆的，也就是，如果你现在处于第 19 个方格，无论你是从第 62 个方格滑下来的，还是在第 14 个方格通过掷骰子掷出 5 来的，下一步的游戏结果都是确定的（即第 19 个方格的概率向量是确定的）。

像这种：无记忆的从一个状态到另一状态的随机过程称之为马尔科夫链或者马尔科夫过程。我们可以使用一个大小为 N * N 的矩阵来描述这一过程，其中 N 代表了系统的状态数量（本游戏中 N = 101）。此矩阵的列向量即为我们之前所说的概率向量。对于矩阵中的任意一个值 (n,m) 其代表了从初始位置 m 到 位置 n 的概率。

下面，让我针对本游戏来产生它的马尔科夫状态转移矩阵：

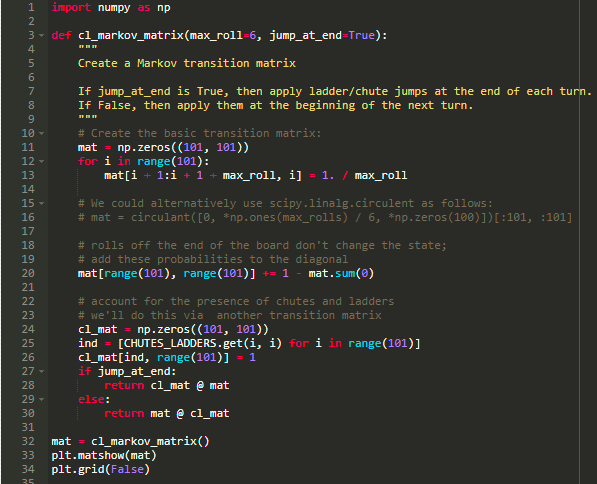
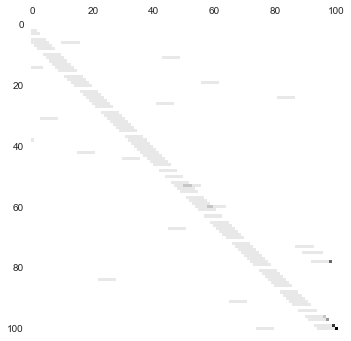
上面的这个矩阵对这个游戏中的所有结果进行了编码。需要注意的是，此矩阵的构造方式有两种：第一种也就是经典玩法，当最后的掷骰子的点数加上当前位置大于一百时，认为走到了终点，游戏结束；另一种则是重新循环，从头开始，针对第二种玩法的我们后面再介绍。

本游戏开始时的状态向量如下所示，这表示初始位置一定是第零位：

仔细的想一想，你就会明白，下一个状态向量就是用 v_0 左乘 状态转移矩阵：

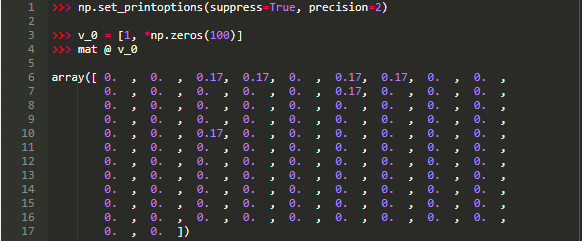
这个结果就是我们之前提及的第一步时的概率向量。

于是乎我们就可以通过不断的左乘状态矩阵来模拟我们每一步的结果。但是这样做的会导致一个计算上的误差，一个更有效的方法就是是矩阵的乘方运算。按照这个思路，下面让我们来计算一下完成这个游戏需要的步数 n 的概率，并将我们的计算结果与之间的进行一个对比。

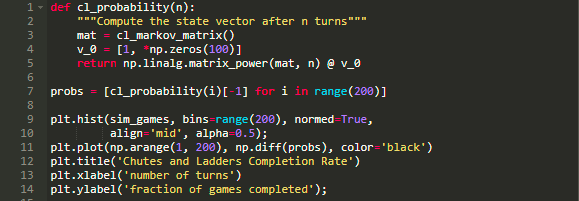
得到结果如下所示：

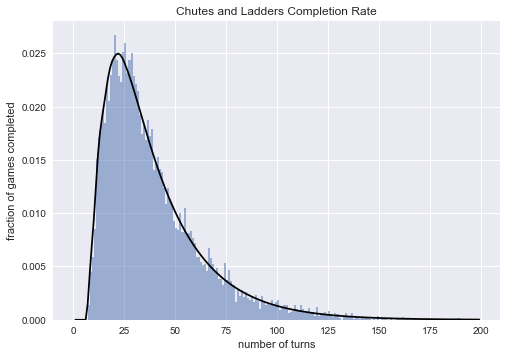
由图可见，我们的直接模拟法得到结果与马尔科夫模型得到的结果非常的相似，这也就意味着我们的思路是正确的。上述分布的累积分布也值得研究研究。

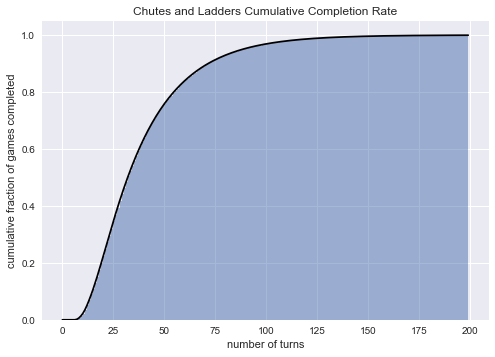
由图可知，百分之九十多的单人玩家基本上可以再 72 步之内完成游戏，当然也存在意外情况。

如果是两位玩家的话，就意味着 72 回合之后游戏仍旧没有结束的概率是 1%。 假设每个回合的时间是 20 秒，那么一局游戏的时间大概是 24 分钟（我个人的经验告诉我情况可能比这个糟糕很多倍）。

游戏的最小时长

如果你的运气足够的好，你最快能多少步完成这个游戏呢？从我们的马尔科夫链模型可以看到，我们有很可能在 7 步之内完成这个游戏，但这个概率很小，大概玩上 660 局游戏才有可能出现这种情况。

马尔可夫链模型并不能告诉我们这个最小步长的具体路径是怎么样的，但是我们可以通过 scipy.sparse.csgraph 来解码这一过程，从而寻找到最短路径：

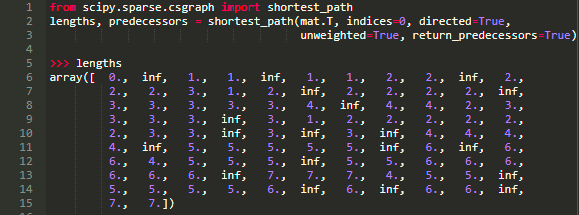
在此 lengths 变量代表了从零开始到其他每个点的最短路径长度。 我们可以使用 predecessors 来重建我们从零到 100 的最短路径：

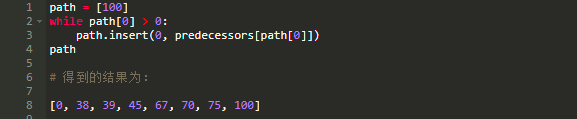
一般情况下的游戏长度

上面呢我们讨论了一下最极端的情况，但是如果我们想要知道的是一般情况下这个游戏的时长是多少该怎么办呢？ 这个问题的的答案取决于所谓的一般情况是什么样的情况。 常用的方法就是取游戏长度的平均值，中间值或者众数。

游戏长度的平均值是指游戏回合数的期望值，即我们对所有存在的可能性进行加权求和。

 由此可知，一局游戏的平均回合数为 39 回合。

在计算平均值时，我们使用的权重是游戏的时长，所有这就使得那些概率很小但是游戏时长很长的样本点对最终结果造成较大的影响。所以，通常情况下，游戏时长的中位数更加具有统计意义：

由此可知，大概 50% 的游戏都会在 32 回合里结束， 另有 50% 的游戏的时长超过了 32 局。但是，不论是平均值还是中位数，其得到的结果与概率分布的峰值所对应的回合数之间都存在一定的差异，其峰值对应的值为：

也就是说，你最有可能在 22 个回合里结束游戏。对于此概率分布来说，最有用的统计量应该是：分位数。

这样告诉我们，大概 95% 的游戏的回合数介于 11 与 106 回合之间。我们也可以简单放宽限制条件：

上面的结果说明：基本上有一半的游戏，其回合数介于 22 与 50 之间。

从马尔科夫过程出发深究

除了那些总体的统计量，本游戏的马尔科夫状态转移矩阵中也蕴含了很多有趣的东西，下面我们一一展示：

香浓熵

我们可以简单的分析一下游戏回合数分布的熵：你可以认为熵是在概率空间中，对游戏回合数分布紧密程度的一种度量。熵值越大，越难估计玩家位置。

我们可以使用 Scipy 里的 stats 模块里的 entropy 函数计算熵值，并将其可视化。我以游戏回合数为自变量，熵值为因变量，画出熵值随游戏回合数的变化曲线：

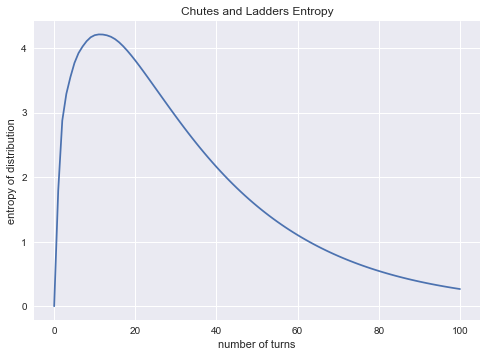
从图可知，当游戏进行到 11 回合时，其熵值最大。这个结果说明，当我们的游戏进行到第 11 回合时，我们可以知此时各个玩家所处的位置位置最为分散。 在此之前，玩家的位置比较接近开始位置；在这之后，玩家位置则比较接近结束位置。

特征值与稳态

从马尔科夫状态转移矩阵中，我们可以了解到整个游戏的动态过程。例如，状态转移矩阵的特征值等于 1 的特征向量给我们展示了什么是稳态。稳态即指经过状态转移矩阵后没有任何变化的状态。

我们可以通过下面的方式计算矩阵的特征向量：

可以看到，在本游戏中只有一个稳态，其为：

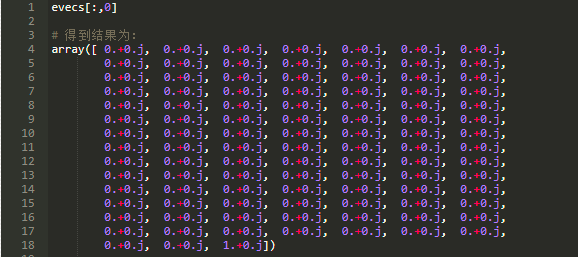
可以看到，这个唯一的稳态代表了游戏结束。这就意味着在本游戏中，你基本上不可能陷入无限的循环中。我怀疑这个游戏的设计者在设计这个游戏的时候就计算过稳态问题，并在这方面获得了意想不到的成功。

基本矩阵

正如我们之前通过状态转移矩阵看到的那样，一旦你到达了终点，你接下来所有的状态都会是 100%。 在数学中，这个游戏的结束状态是一个“收敛态”，也就是说一旦你达到了这个状态，你就不能跳转到其他的状态了。这也就是说，梯子与滑梯游戏是一个“收敛的马尔科夫链”，基于这一点，针对状态转移矩阵，我们还可以做点其他的分析。

首先需要计算收敛马尔科夫链的基本矩阵 N，它是马尔科夫状态转移矩阵的一个简单的变形：

在矩阵 N 中，位于 (n, m) 元素的值代表了每局游戏中，从方格 m 出发到方格 n 所需的平均回合数。下面我们画出从零出发到各个方格所需的回合数：

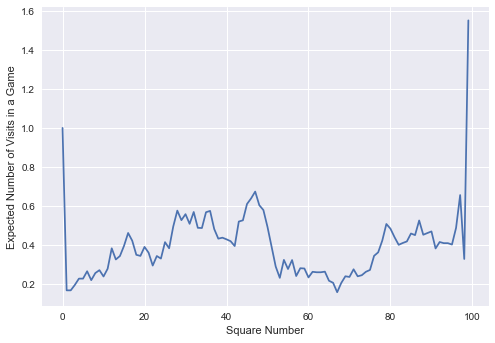
上图得到的结果很有意思，从图我们可以看出，从零出发，每局游戏中，你到达第 99 个方格的平均次数是 1.5 次。这是因为，一旦你到达了第 99 个方格，你就不得不掷出 1 来，否则没法离开这个方格，而其他的当你位于位置时，你并没有这样的束缚条件。

我们看一看访问次数较多的几个方格分别是哪几个：

除过第 99 个方格，下一个访问次数最多的方格便是第零个方格，每局游戏中，一开始的时候都会访问一次此方格。排名第三的是第 47 个方格，每局游戏中，平均访问次数为 3/4。且此方格位于滑梯的顶端，因此可知此滑梯是整个游戏中最常用的滑梯。

我们也可以看一看访问次数最小的几个方格是哪几个：

令人奇怪的是，访问次数最少的方格竟是第 67 个方格，它的访问次数竟然比第 1 个方格还小，每局游戏中，访问方格 1 的概率大于零，此情况出现在一开始时，我们掷出的点数为 1。从上图可知，由于游戏中梯子与滑梯位置的缘故，方格 55-75 的访问次数相对较小。

大滑梯与大梯子

对于我的小女儿来说，她最关心的是：每局游戏中，能碰见多少次“大滑梯”或者“大梯子”？ 它们分别位于第 87 和第 28 个方格。

我们可以看到，平均每两局我们就会遇见一次“大滑梯”，而遇见“大梯子”的概率则略微高一点点，即每十局游戏中，大概有 6 局游戏可以遇见“大梯子”。

收敛时间

基本矩阵也可以用于计算其他的性质，例如将一个全为 1 的列向量与矩阵左乘，即可得到收敛时间。其代表了从当前状态到游戏结束所需要的回合数。下面我们再一次使用上面计算出的基本矩阵：

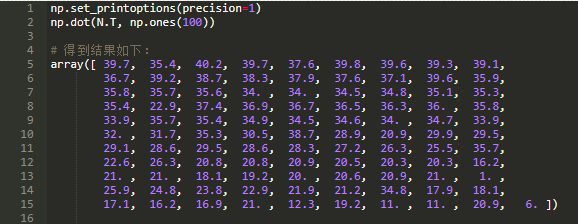
对于第一个方块位置，大概需要 39.7 步才能完成游戏，这比我们之前计算的结果值 39.2 步要大半步， 这是因为我们使用的是不同的形式的矩阵（此处我们将从 80 到 100 方格的爬梯子记为额外的回合数）。

这个向量告诉我们一个件事，那就是第一次掷骰子最好掷出 1，然后通过第一个梯子爬升，这也跟我女儿的直觉是一致的。，这样可以减少你完成游戏的回合数。第一次掷骰子最好不要掷出 2，这将平均增加你 0.5 个回合数。一开始掷出 2 会让你远离最终的目标。

当你走到第 99 个方格时，距离成功的平均步数时 6 步，因为你有 1/6 的机会掷出 1 然后赢得游戏。往后退两格，也就是你位于第 97 个方格，此时期望的步数是 11 步之所以变大，是因为在第 98 个方格处还存在一个滑梯。

基本矩阵能够让你了解到此游戏的其他一些性质，例如，我们可以调整次矩阵，把第 80 个方块作为一个结束点，并计算出通过它直接到达第 100 个方块的概率。 或者我们也可以通过此矩阵计算每个格数的访问次数与游戏回合数关系的方差。 更多关于收敛马尔科夫链基本矩阵的应用可以参考维基百科。 关于这些概念的一个基础教程可以参考 Grinstead 与 Snell 合著的 《Introduction to Probability》 的第十一章。

可视化游戏过程

仅仅为了好玩，下面我们使用 Python 工具来可视化整个游戏的可能状态。我们将使用一开始介绍的梯子与滑梯游戏的图纸作为背景，使用可变透明度的经典颜色来在图上画出游戏中可能的状态分布。

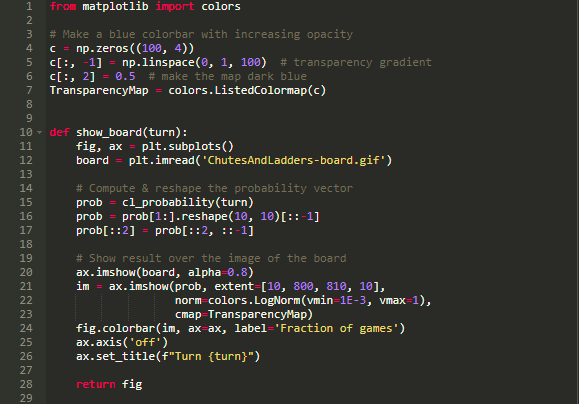
使用上面的这个函数，我们可以可视化任意回合的状态分布情况：

以上两个函数调用得到的结果分布如下所示：

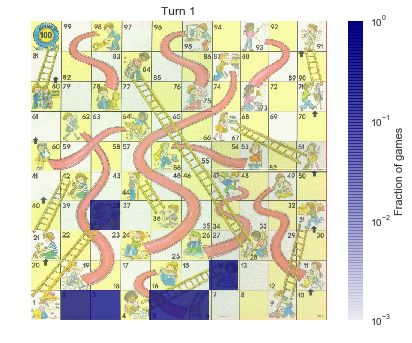
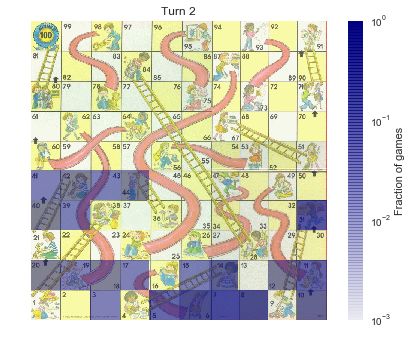
在第一回合后，可能的状态分布还是很紧凑的，仅仅有 6 种可能的分布。在第二回合后，虽然可能的状态数并不多，但是其分布已经变得更加离散。

以上两个函数调用得到的结果分布如下所示：

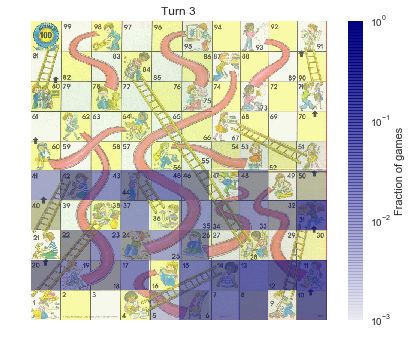
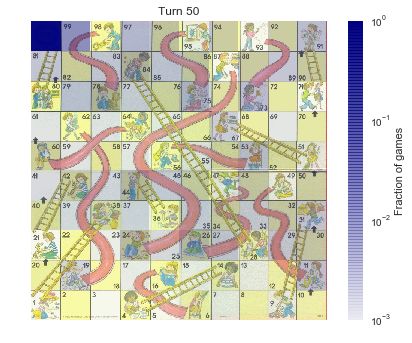
第三回合后，分布变的更加离散。当游戏进行到 50 回合以后，大部分游戏已经结束了，但是仍旧存在一些没有结束的情况。

动画模拟

如果我们能将上述每一回合的结果整合成一个动画的形式，那么效果可能会更加直观。下面我使用 ImageIO 这个库来将所有的基于 matplotlib 得到的结果进行整合形成一个 GIF 格式的图片。（当然你可以使用 matplotlib 进行这一整合操作，但是它需要一些其他的命令行参数，但是 ImageIO 则不需要）

下面我们从一个函数开始，这个函数基于 ImageIO 库，其作用是从 matplotlib 图片产生 GIF 图像：

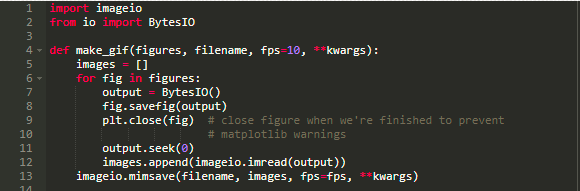
接下来我们就可以进行模拟来产生 GIF 图像了。我相应地调整每帧之间的延时，从而使得前期的几帧图像更加明显：

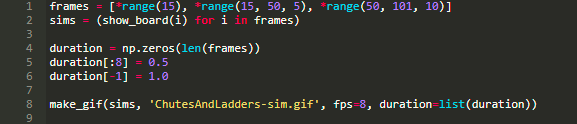
我们得到的最终的 GIF 图像如下所示：

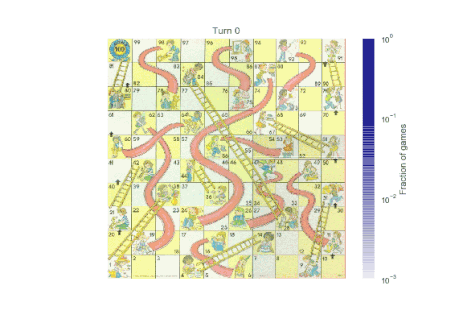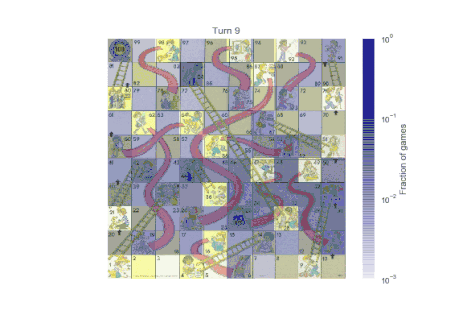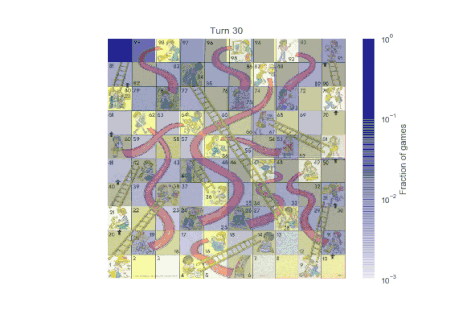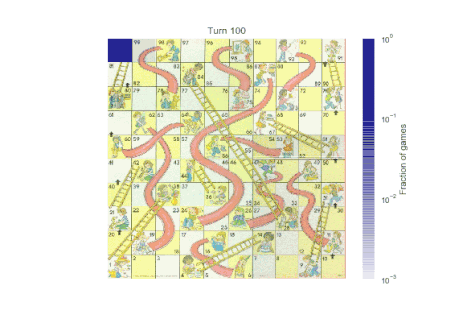
结论

我希望你能从这篇文章中有所收获，如果你没有，我相信你至少是认同我所做的工作的。最后额外的说一点：如果过些年后，你无意间发现了这篇文章，我希望你能和我一样，多陪陪你的孩子，玩玩这个游戏，并体会一下其中的乐趣。

谢谢观看~

英文原文：https://jakevdp.github.io/blog/2017/12/18/simulating-chutes-and-ladders/
译者：无