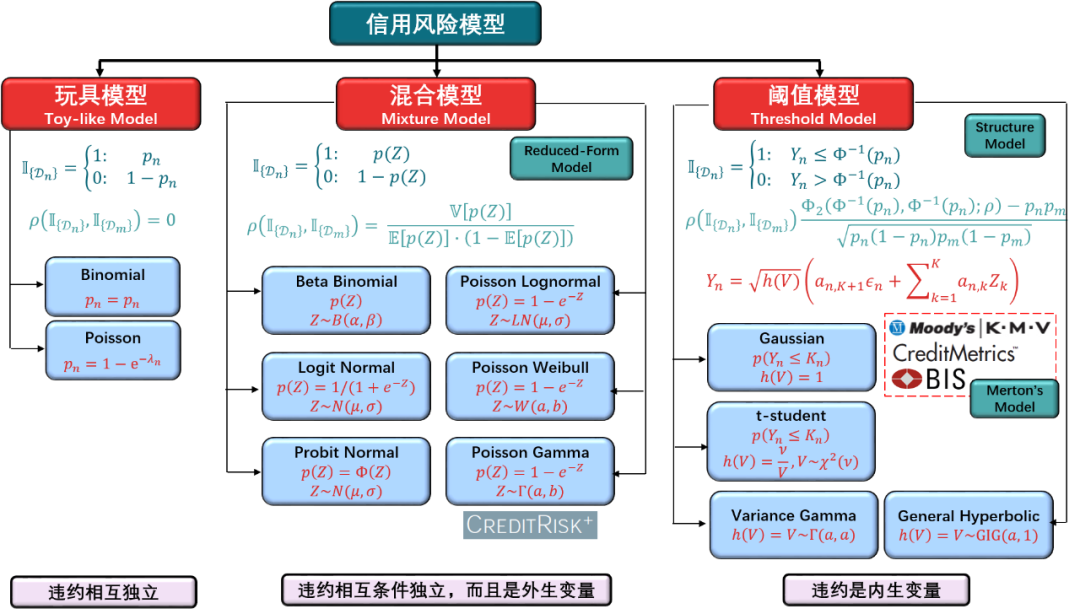
本文是「信用风险建模 in Python」系列的第三篇,其实在之前的 Cufflinks 那篇已经埋下了信用风险的伏笔,
信用组合可视化
信用风险 101
独立模型 - 伯努利模型
独立模型 - 泊松模型
在伯努利模型中,我们用一下违约指示函数来对第 n 个借贷人违约建模

这种建模方式是直接赋值给违约事件和存活事件一个概率,但并没对违约事件建模。如果要做的更精细点,我们可以引进随机变量 Xn,定义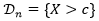 为违约事件,即当随机变量超过一个阈值时违约,那么违约指示函数为
为违约事件,即当随机变量超过一个阈值时违约,那么违约指示函数为
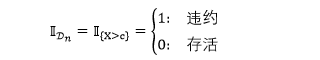
该随机变量 Xn 可以是离散型或连续性,以上这种指定违约的模式打开了很多的建模可能性。如果以伯努利分布(二项分布)为起点,我们很自然的会联想到泊松分布 (Poisson distribution),该分布是对一段时间某种事件发生的次数建模的。如果把事件想成违约,那么该事件发生一次和一次以上就是违约,即 Xn ≥ 1,发生零次就是存活,即 Xn < 1。
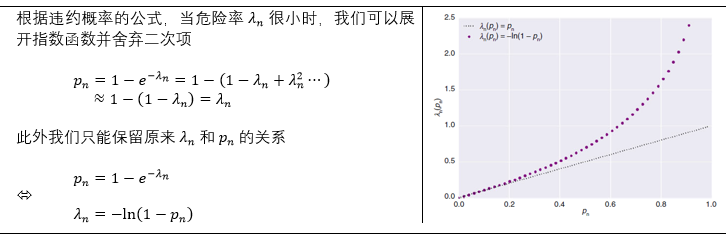
根据泊松分布的 CDF,我们得到
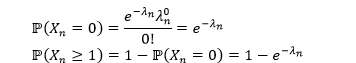
那么违约个数为泊松分布对应的违约指示函数为

接下来我们分别从数值法、解析法来分析泊松模型。首先引入所需的 Python 包。
上式的随机变量 Xn 服从泊松分布,模拟方法如下图所示:
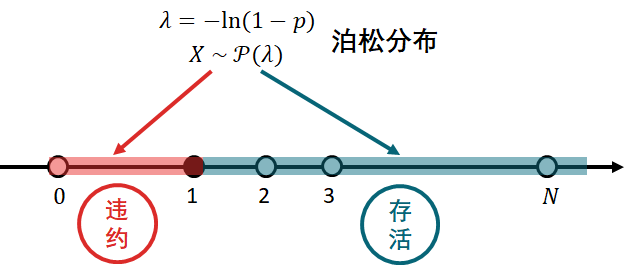
假设有 M 个模拟路径,N 个借贷人,那么对 n =1, 2, …, N 和 m= 1, 2, …, M, 我们需要模拟出 NM 个违约指标。
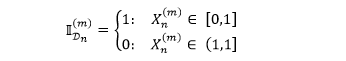
剩下的操作就简单了,对于第 m 个模拟情境,计算出组合损失
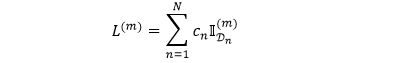
将上面过程重复 M 遍得到 L(1), L(2), …, L(M),再根据均值和方差的定义来计算它们(用 hat 表示它们是估计量而不是数学定义)
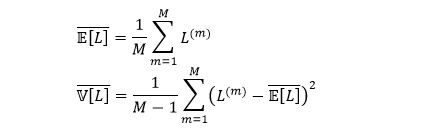
只要 M 够大,上面这些计算出来的值可以近似当成真实值。
我们还是用之前提到的样本组合(sample portfolio),它包含 100 个不同的借贷人,有如下三个假设:
组合的总规模为 1000,意味着平均每个借贷人的敞口(exposure)为 10。
实际敞口是根据韦伯分布(Weibull)模拟得出,范围从小于 1 到 50。
借贷人的无条件违约概率(unconditional default probability)根据卡方分布(chi-square)模拟得出,均值设为 1%。
我模拟好违约率和敞口存成两个 numpy 格式文件 expFile 和 dpFile,加载存储成变量 p 和 c,此外
c = np.load(expFile) p = np.load(dpFile)N = len(c)M = 1000000q = [0.95, 0.97, 0.99, 0.995, 0.999, 0.9997
, 0.9999]q_style = [str(i*100) +'%' for i in q]money_fmt = '${0:,.2f}'number_fmt = '{0:,.2f}'
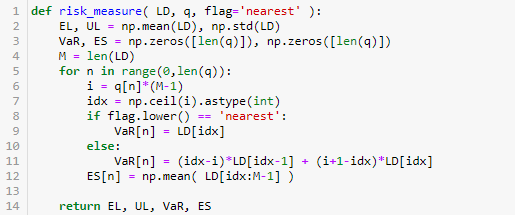
编写三个函数,分别计算损失分布(poisson_LD),计算风险指标(risk_measure)和整体模拟(poisson_simulation)。代码很简单,按照 1.1 的公式和逻辑就能轻易实现。
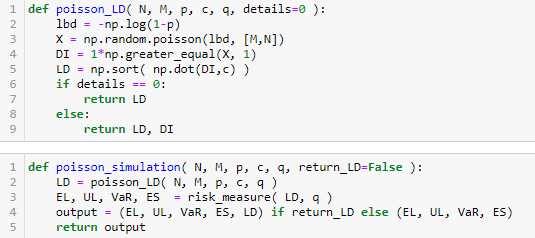
运行来生成 EL, UL, VaR 和 ES。
EL, UL, VaR, ES = poisson_simulation( N, M, p, c, q )
打印出在不同置信度下的 VaR 和 ES 值,都是递增的。
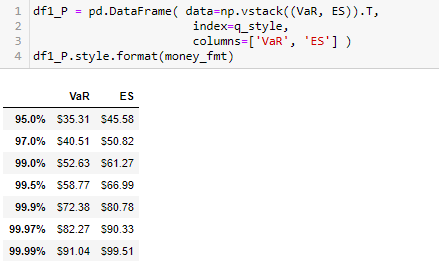
打印出该组合的 EL 和 UL 值,它们对于不同的置信度的都是一样的。我们可以看出极端损失(VaR, ES)要比 UL 大,因此损失波动率并不是一个可能捕捉注组合风险的好指标。
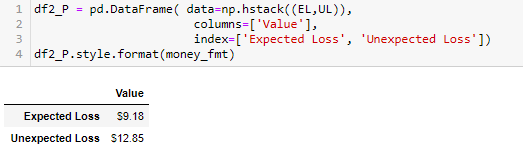
和上贴【伯努利模型】的蒙特卡洛模拟方法类比,将泊松模型的模拟方法总结在下表。
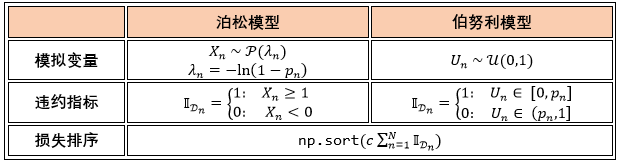
比较两个模型结果发现非常相近。
c = np.load(expFile) p = np.load(dpFile)q = np.array([0.95,0.97,0.99,0.995,0.999,0.9997,0.9999])M = 1000000models = [binomial_simulation, poisson_simulation]simulation_model( M, p, c, q, models )
数值解
q VaR_b
ES_b VaR_p ES_p
95.00th 35.2 45.4 35.2 45.4
97.00th 40.3 50.7 40.2 50.6
99.00th 52.5 61.0 52.4 61.1
99.50th 58.7 66.6 58.7 66.7
99.90th 71.6 79.7 71.7 80.5
99.97th 81.5 88.7 82.4 90.5
99.99th 89.7 96.9 90.5 99.5
Expected loss: 9.2 vs. 9.2
Loss volatility: 12.8 vs. 12.8
CPU Time: 4.3
vs. 6.8
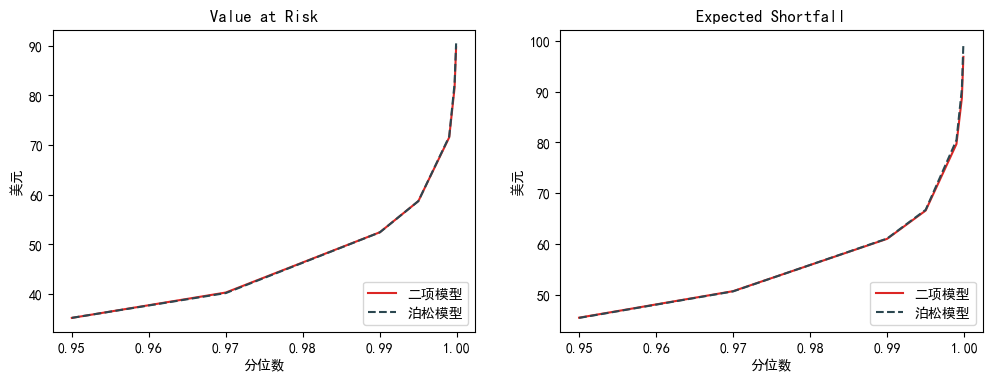
画出两个模型模拟出来的损失分布图也非常相似(尤其在尾部)。
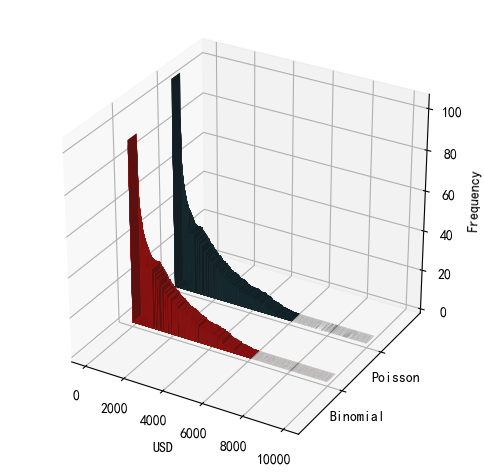
这是巧合吗?
推导解析解时需要做进一步模型假设,即假设所有借贷人的违约概率和损失暴露都相等,这只适用于借贷人很多的“大型风险分散”组合。对于 N 个借贷人,我们有
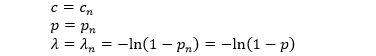
这是组合损失可以简化成
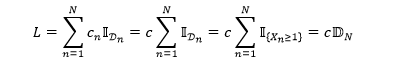
其中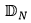 是整个组合违约的个数(不一定是整数),它是由一组独立同分布的“泊松变量构成的指示函数”加总而得。当 λ 很小时,我们有
是整个组合违约的个数(不一定是整数),它是由一组独立同分布的“泊松变量构成的指示函数”加总而得。当 λ 很小时,我们有
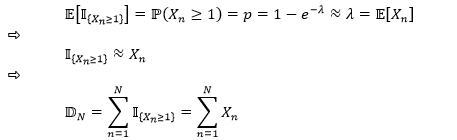
第一步推导用到了泊松分布的性质;第二步推导认为当 λ 很小时,Xn 可近似看成一个二元变量,一种情况等于 0 (概率很大为 1– p),一种情况等于 {1,2,3, …} (概率很小为 p)。第三步应用推导结果把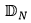 写成一组独立同分布的“泊松变量”的总和,它还是一个泊松变量。这是非常好的结果,我们可以轻易写出
写成一组独立同分布的“泊松变量”的总和,它还是一个泊松变量。这是非常好的结果,我们可以轻易写出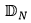 的性质。带着上贴【伯努利模型】二项分布的
的性质。带着上贴【伯努利模型】二项分布的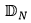 ,下表一起做个总结。
,下表一起做个总结。

接下来对比两种分布下的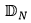 在样本信用组合上的各项指标。
在样本信用组合上的各项指标。
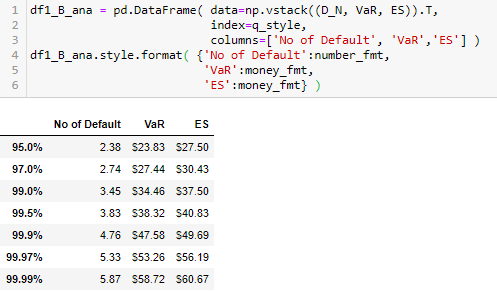
编写一个函数,计算泊松分布分布的 EL, UL, PMF, CDF, VaR, ES 以及组合违约总个数 DN,代码也不难,PMF 和 CDF 直接用 scipy.stats 里面的函数
DN 跟 quantile 有关,把 CDF 当做自变量,个数当做变量,线性插出就行
VaR 就是 c 乘上 DN ,因为我们把损失整数离散化了
ES 稍微麻烦点,但对于每个 quantile qi,将 qi 到 1 分 1000 个点,然后求出均值

根据之前的假设,p 和 c 对于所有借贷人都是一样的,有 100 个借贷人,p 和 c 分别为整个组合所有借贷人违约概率和敞口的均值。
c = np.load(expFile) p = np.load(dpFile)(N, p, c) = (len(c), np.mean(p), np.mean(c))q = np.array([0.95,0.97,0.99,0.995,0.999,0.9997,0.9999])
打印出在不同置信度下的违约总个数 DN,VaR 和 ES 值,都是递增的。
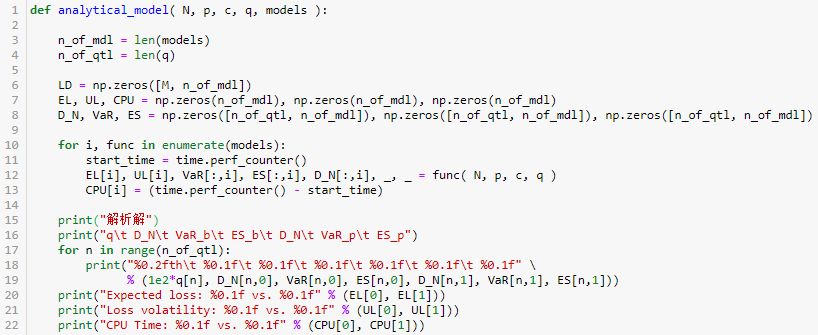
c = np.load(expFile) p = np.load(dpFile)(N, p, c) = (len(c), np.mean(p), np.mean(c))q = np.array([0.95,0.97,0.99,0.995,0.999,0.9997,0.9999])models = [binomial_analytical, poisson_analytical]analytical_model( N, p, c, q, models )
解析解
q D_N VaR_b ES_b D_N VaR_p ES_p
95.00th 2.4 23.8 27.5 2.4 24.1 27.7
97.00th 2.7 27.4 30.4 2.8 27.6 30.7
99.00th 3.4 34.5 37.5 3.5 34.9
37.9
99.50th 3.8 38.3 40.8 3.9 38.6 41.2
99.90th 4.8 47.6 49.7 4.8 48.0 50.2
99.97th 5.3 53.3 56.2 5.4 54.3 57.0
99.99th 5.9 58.7 60.7 5.9 59.1 61.4
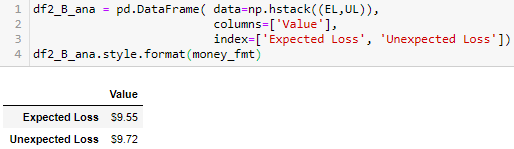
Expected loss: 9.5 vs. 9.6
Loss volatility: 9.7 vs. 9.8
CPU Time: 0.0 vs. 0.0

和预期一样,结果尽管不是完全一致,但是非常接近。数值法和解析法在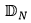 为二项分布和泊松分布的产出都这么接近,为什么两个完全不同的模型产出这么接近?这是巧合吗?难道这两个模型在某些条件下是等价的?
为二项分布和泊松分布的产出都这么接近,为什么两个完全不同的模型产出这么接近?这是巧合吗?难道这两个模型在某些条件下是等价的?
二项模型有两个参数 p 和 N,而泊松分布只有一个参数 λ,为了能比较两者,需要想个办法统一它们的参数,比如设置 λ= Np。接下来我们来比较 B(p, N) 和 P(λ)。
当 p 足够小和 N 足够大时,二项分布逼近泊松分布。从二项分布的 PDF 开始,将 p = λ/N 带入,并求得当 N 趋近无穷时的极限。证明过程如下:

我们采取两组实验来验证上面结论,设置 N = 100,
情况一:p = 0.01,两个分布非常相似
情况二:p = 0.25,两个分布差别不小
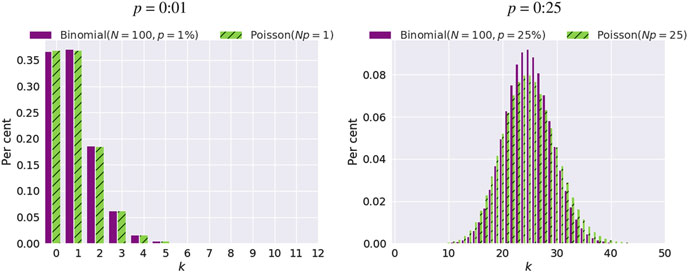
当 p = 0.25 时,两个模型的解析解产出对比如下:
c = np.load(expFile) p = np.load(dpFile)(N, p, c) = (len(c), 0.25, np.mean(c))q = np.array([0.95,0.97,0.99,0.995,0.999,0.9997,0.9999])models = [binomial_analytical, poisson_analytical]analytical_model( N, p, c, q, models )
解析解
q D_N VaR_b ES_b
D_N VaR_p ES_p
95.00th 31.8 317.8 329.0 37.4 373.9 388.2
97.00th 32.9 328.6 338.9 38.8 387.8 401.0
99.00th 34.9 349.2 358.2 41.5 414.9 426.3
99.50th 36.1 360.7 369.3 43.0 429.8 440.8
99.90th 38.6 385.6 392.5 46.2 462.3 471.8
99.97th 40.1 401.4 408.2 48.4 484.3 492.9
99.99th 41.6 415.7 421.5 50.3 502.8
511.1
Expected loss: 250.0 vs. 287.7
Loss volatility: 43.3 vs. 53.6
CPU Time: 0.0 vs. 0.1
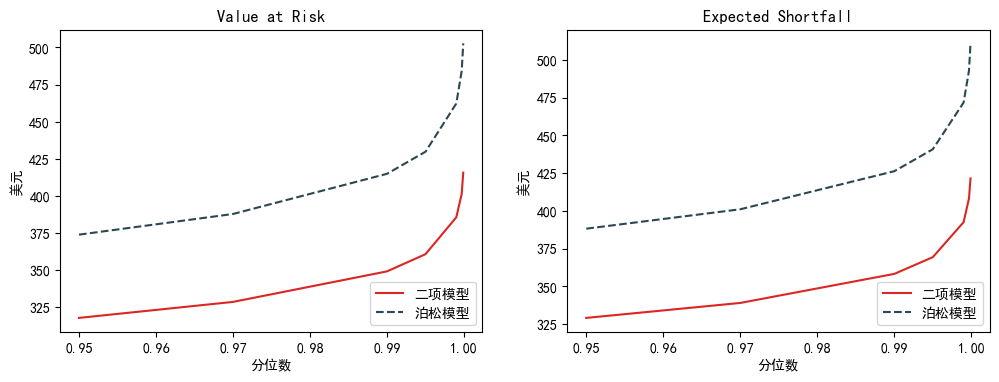
当 p = 0.25 时,差别很大,两个模型的表现不再一致,泊松模型在每个分位数下计算出的 VaR 和 ES 比二项模型的都大。
渐进模型那章中证明的结果称为罕见事件定理(law of rare event),它有什么用呢?接下来我们会遇到很多模型都是以二项分布为起点,但是用泊松分布来建模。背后的原因就可以用罕见事件定理来解释。
不过同时也要清楚认识到,独立二项模型不等于独立泊松模型。它们都有瘦尾、渐进行为稳定、违约独立这三大特点,但也不是一无是处,它们简单易懂,而且可以作为复杂模型的基准。进一步讲,它们可当为违约风险的下界,在做模型诊断(model diagnostics)中起着重要的作用。
之后会介绍由 Frey 和 McNeil 在 2003 年设计的混合模型(mixtured model),该模型认为违约是个随机事件,通过用一个混合分布来引入违约相关(default dependence)并能捕捉到肥尾事件(fail-tail event)。
Stay Tuned!