最近看到一个post很有意思啊,于是我自己动手练习了一遍,但由于最近比较忙所以这就随便记录一下学习心得和脚本测试,更多详细的改进后面慢慢再看了,练习的时候还是建议一条一条脚本的去执行,这样才能更好地知道脚本的含义和前后逻辑关系。突然发现,经过这个练习,收获不少呀
So,这部分就是学基于Python学习快速傅里叶变换(FFT)和连续小波变换(CWT),其实还可以做离散小波变换的。
使用的数据是纯文本形式的季风相关的数据,网址:https://mol.tropmet.res.in/monsoon-interannual-timeseries/
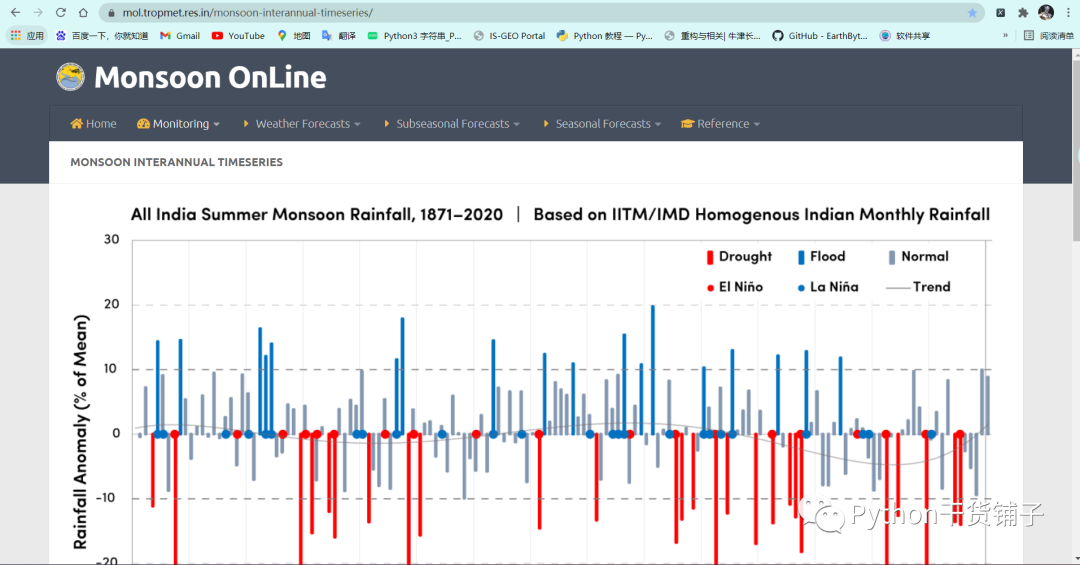
打开后这样的:
那么就开始处理流程,首先是pandas读取它,这部分很简单了,由于使用的是原post的格式就没变化多少,主要是信号切片那里手动换一下
import pywtimport numpy as npimport matplotlib.pyplot as pltimport pandas as pdplt.style.use('seaborn')
dataset = "./monsoon.txt"df_nino = pd.read_table(dataset,header=None)df_nino
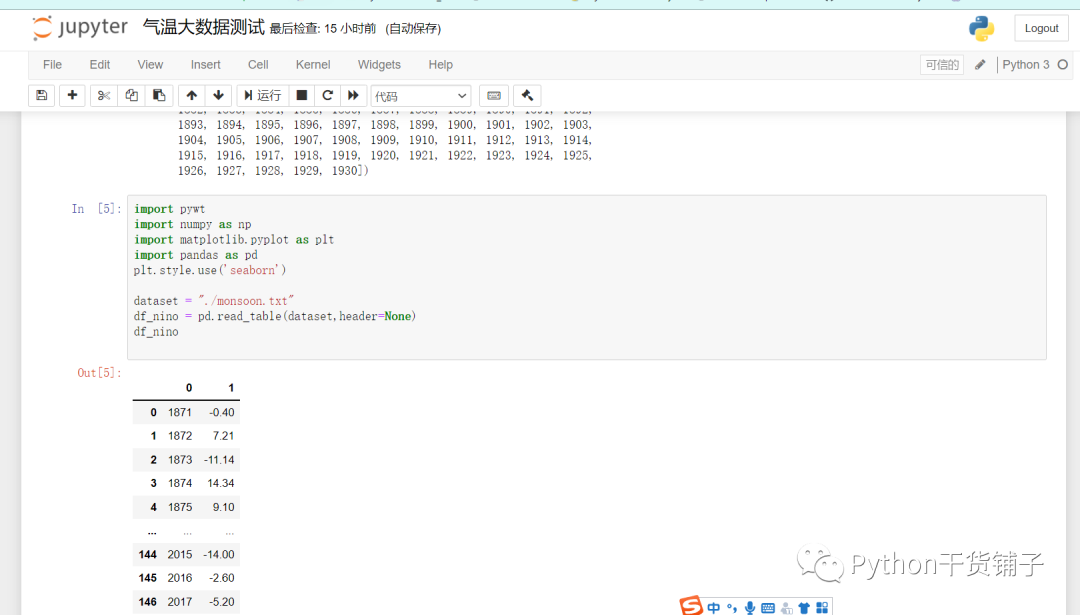
具体注释的看截图了,没时间具体写了
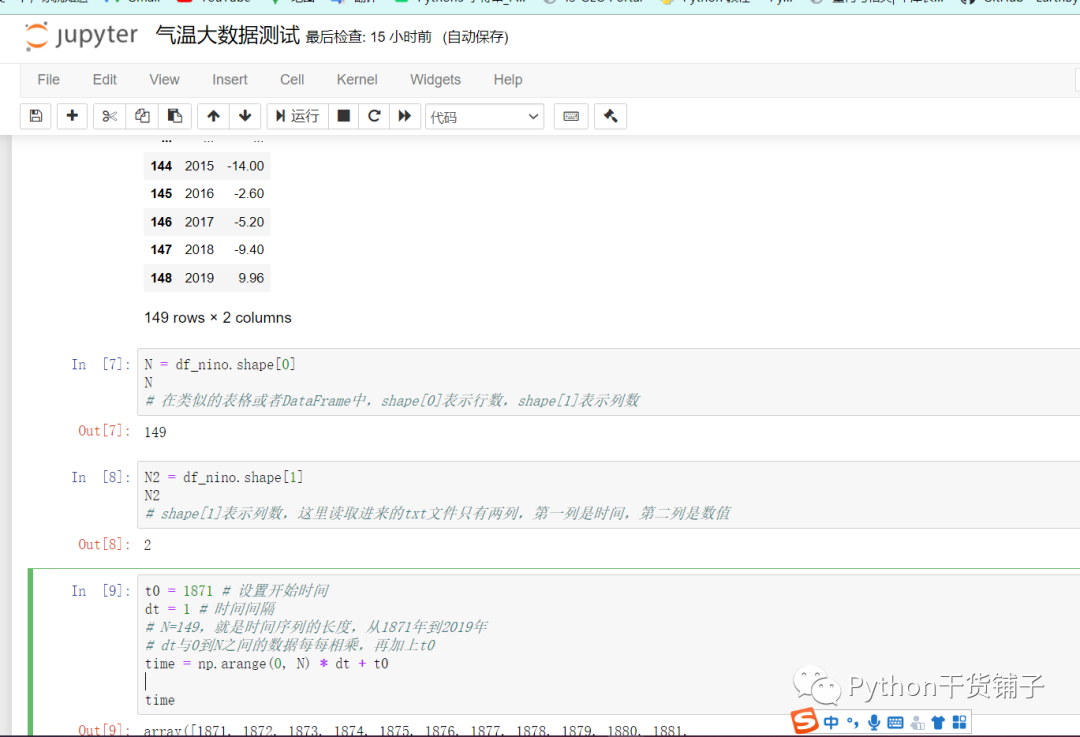
绘制出来看看长什么样:
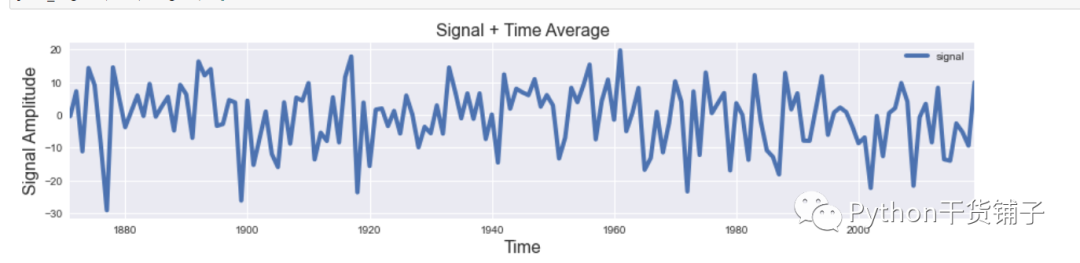
def plot_signal(time, signal, average_over=5, figname=None): fig, ax = plt.subplots(figsize=(15, 3)) ax.plot(time, signal[:,1:], label='signal',lw=4.0) ax.set_xlim([time[0], time[-1]]) ax.set_ylabel('Signal Amplitude', fontsize=16) ax.set_title('Signal + Time Average', fontsize=16) ax.set_xlabel('Time', fontsize=16) ax.legend() plt.show()
plot_signal(time, signal)
由于读取的txt是两列的,所以取值的时候,第一列是时间,就行全取,然后第二列全取[:,1:],其他的就是基本设置了
FFT部分:
def get_fft_values(y_values, T, N, f_s): f_values = np.linspace(0.0, 1.0/(2.0*T), N//2) fft_values_ = np.fft.fft(y_values) fft_values = 2.0/N * np.abs(fft_values_[0:N//2]) return f_values, fft_values
def plot_fft_plus_power(time, signal, figname=None): dt = time[1] - time[0] N = len(signal) fs = 1/dt fig, ax = plt.subplots(2, 1, figsize=(15, 6), sharex=True) variance = np.std(signal[:,1
:])**2 f_values, fft_values = get_fft_values(signal[:,1:], dt, N, fs) fft_power = variance * abs(fft_values) ** 2 ax[0].plot(f_values, fft_values, 'r-', label='Fourier Transform') ax[1].plot(f_values, fft_power, 'b-', linewidth=1, label='FFT Power Spectrum') ax[1].set_xlabel('Frequency [Hz / year]', fontsize=18) ax[1].set_ylabel('Amplitude', fontsize=12) ax[0].set_ylabel('Amplitude', fontsize=12) ax[0].legend() ax[1].legend() plt.show()
plot_fft_plus_power(time, signal)
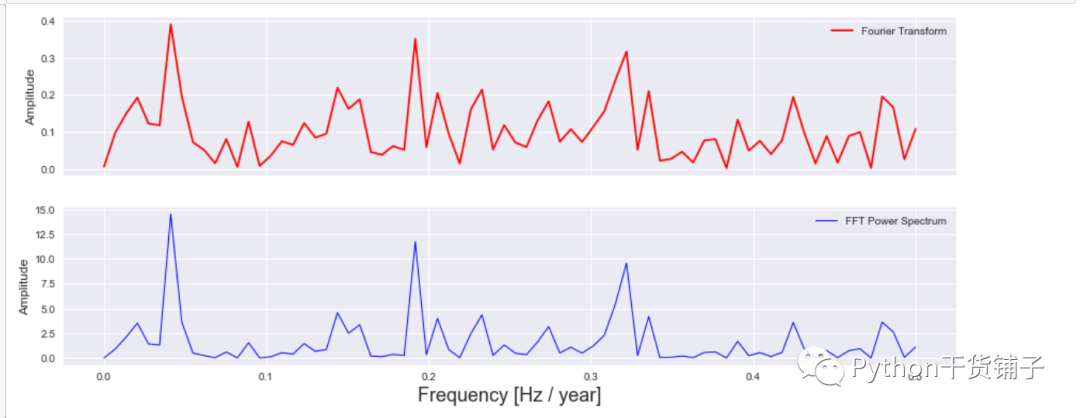
最后就是连续小波变换部分了,可以有连续的和离散的两种,可以选择不同的小波基函数
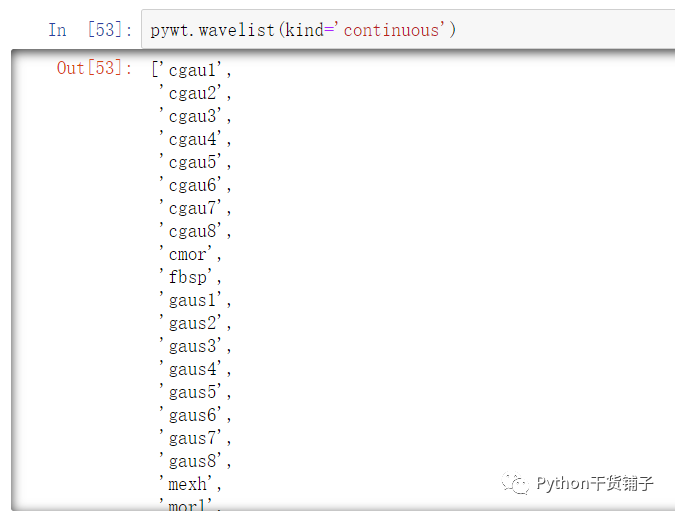
比如这里我选择了mexh测试
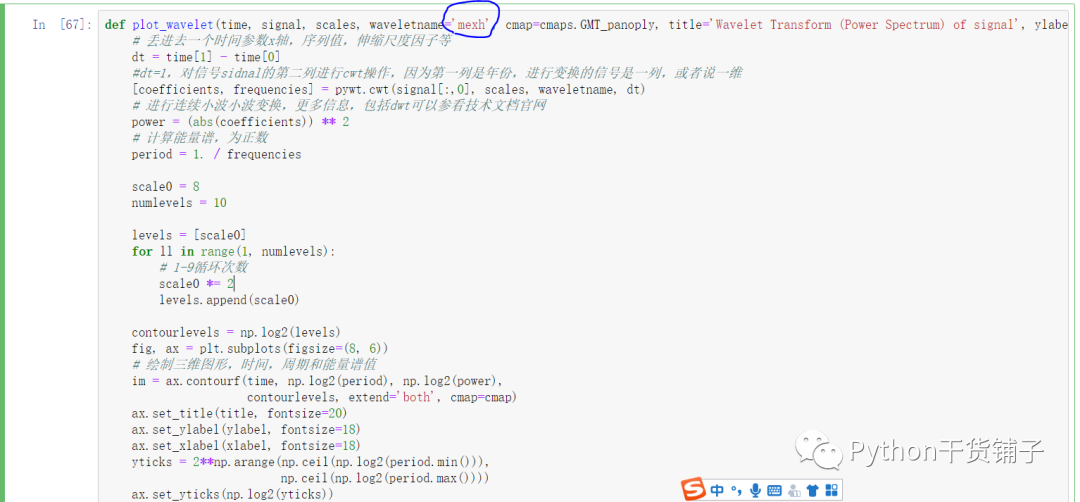
def plot_wavelet(time, signal, scales, waveletname='mexh', cmap=cmaps.GMT_panoply, title='Wavelet Transform (Power Spectrum) of signal', ylabel='Period (years)', xlabel='Time', figname=None): dt = time[1] - time[0] [coefficients, frequencies] = pywt.cwt(signal[:,0], scales, waveletname, dt) power = (abs(coefficients)) ** 2 period = 1. / frequencies
scale0 = 8 numlevels = 10
levels = [scale0] for ll in range(1, numlevels): scale0 *= 2 levels.append(scale0)
contourlevels = np.log2(levels) fig, ax = plt.subplots(figsize=(8, 6)) im = ax.contourf(time, np.log2(period), np.log2(power), contourlevels, extend='both', cmap=cmap) ax.set_title(title, fontsize=20) ax.set_ylabel(ylabel, fontsize=18) ax.set_xlabel(xlabel, fontsize=18) yticks = 2**np.arange(np.ceil(np.log2(period.min())), np.ceil(np.log2(period.max()))) ax.set_yticks(np.log2(yticks)) ax.set_yticklabels(yticks) ax.invert_yaxis() ylim = ax.get_ylim()
cbar_ax = fig.add_axes([0.95, 0.15, 0.03, 0.7]) fig.colorbar(im, cax=cbar_ax, orientation="vertical") plt.show()
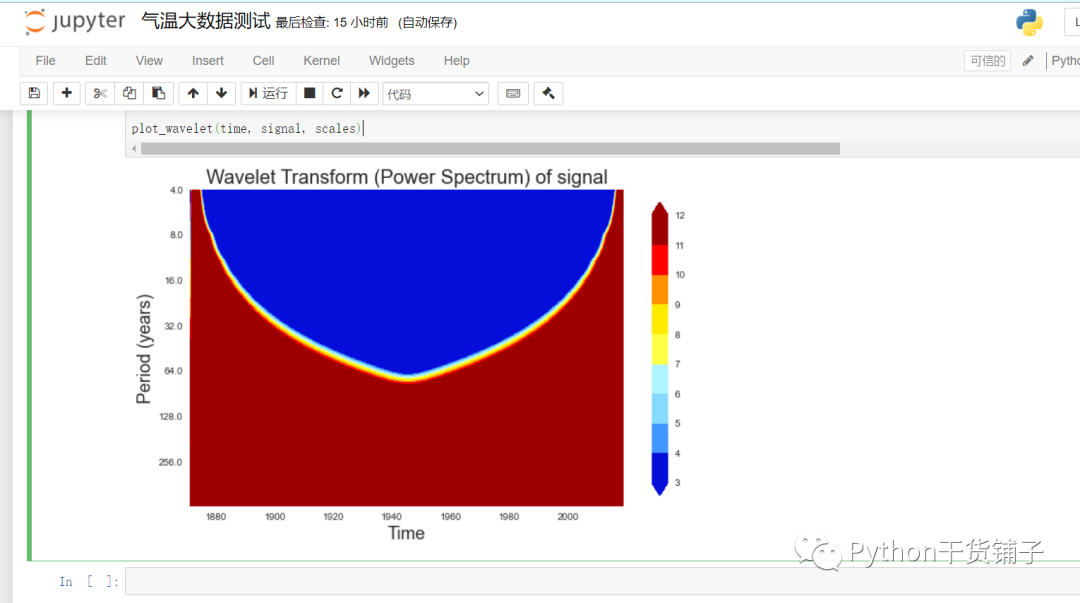
plot_wavelet(time, signal, scales)
获得结果图,看起来好像有问题呀,这是昨晚做的测试了,时间仓促,有兴趣的可以去尝试一下DWT和CWT或者换其他基函数测试他们之间的差异看看。好吧,就到这里了,在这里你将会更喜欢Python的模块化编程方式,,,,还有其他的一些学习收获