代码共享 | 基于Python的序列(txt)与场相关(netcdf)

相关分析在许多学科中都是非常常见的一种研究方法，几乎无处不在。最近看到一篇文章发现很有意思，决定分享出来，这篇文章附带的Python代码是开源的。文中作者使用古气候文献中的例子来强调虚假相关性如何影响古气候代用资料的解释。在某些情况下，之前研究声称重要的相关性被是不重要的，从而对已发表的解释提出了挑战。结论是，仅仅统计数据并不能证实一个proxy的真实性，作者建议对代理信号建立机理上的理解，作为解释的更Robust的基础。大白话就是我们不能只看到相关系数好，而应该更多地从机制上解释为什么会如此。话说回来，平时我们看到的多数paper好像多数就是这么说的，动不动就说相关性好，却老是不解释一下。。。。。。。。。。

具体的开源Python测试代码,使用的数据是降水和OLR的格点数据，这是三维数据，另一个是存储在txt中的纯文本数据

%matplotlib inlinefrom mpl_toolkits.basemap import Basemapfrom scipy.stats.mstats import mquantilesfrom scipy.stats.stats import pearsonrfrom scipy import interpolatefrom scipy.interpolate import UnivariateSplinefrom scipy.signal import butter, lfilter, filtfiltimport matplotlib.pyplot as pltimport numpy as npfrom numpy import genfromtxtfrom nitime import algorithms as algfrom nitime import utilsfrom scipy.stats import timport xarray as xrimport pandas as pdfrom rpy2.robjects import FloatVectorfrom rpy2.robjects.vectors import StrVectorimport rpy2.robjects as robjects    from rpy2.robjects.packages import importrr = robjects.r

#plt.style.use('ggplot')
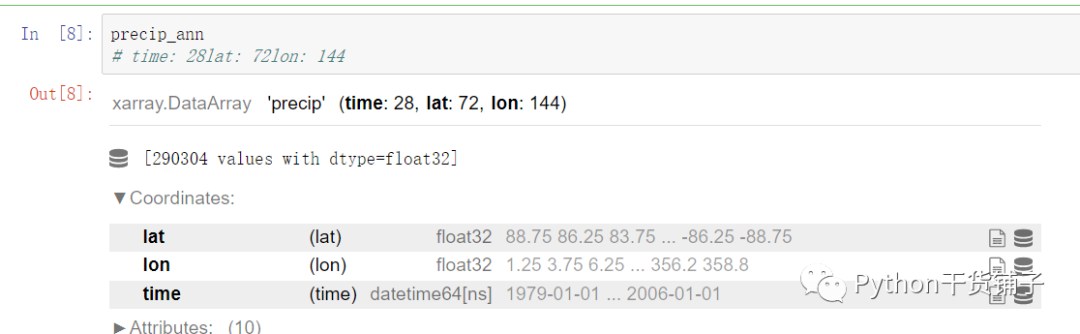
#read CMAP precipitationnc = xr.open_dataset('data/precip.mon.mean.nc')lat0 = nc['lat']lon0 = nc['lon']precip = nc['precip']nlat=lat0.shape[0]nlon=lon0.shape[0]precip_ann=precip[0:335:12,:,:]
#read NOAA OLRnc = xr.open_dataset('data/olr.mon.mean.nc')lat1 = nc['lat']lon1 = nc['lon']olr0 = nc['olr']olr0 = olr0*0.01+327.65olr = olr0[55:390,:,:]olr_ann = olr0[55:390:12,:,:]

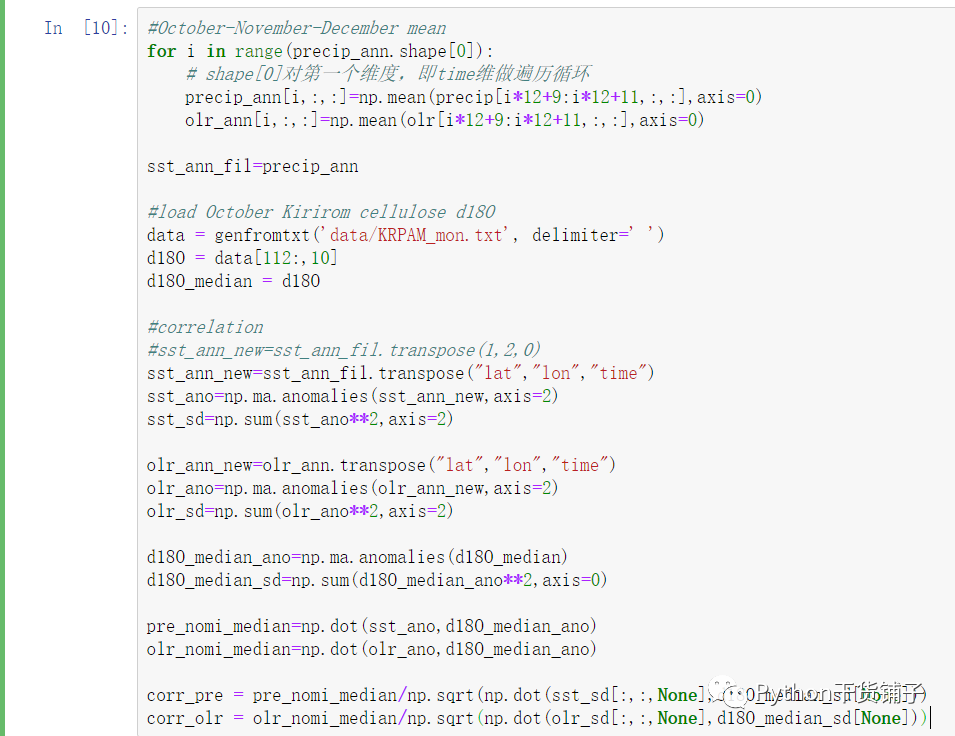
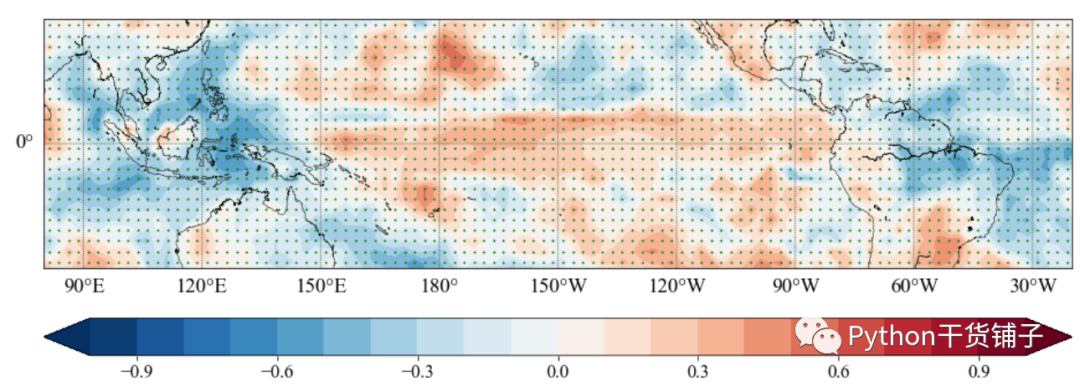
场相关结果：

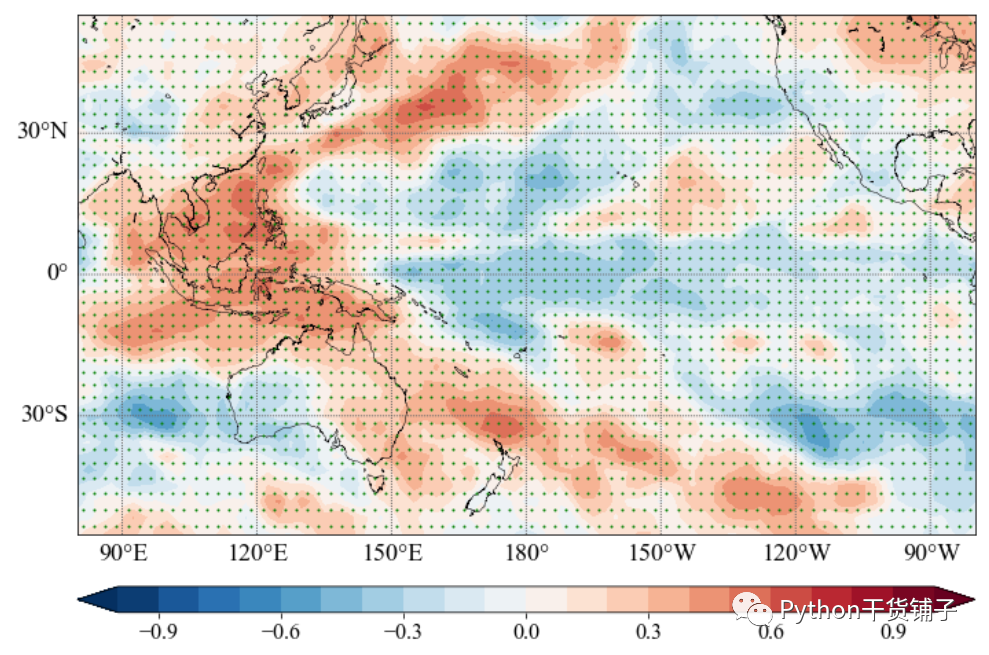
其他具体的信息可以去查看一下这个开源代码，感觉不是那么easy