以下全文代码均已发布至和鲸社区,复制下面链接或者阅读原文前往,可一键fork跑通:
https://www.heywhale.com/mw/project/61bc71dc7e520c001798e15a?shareby=6194fef0f4be9e0017857668
最早的客观分析是利用多项式插值将观测资料插值到模式的规则网格,但是观测资料较为稀疏,没有充足的资料用做模式的初始化,利用空间插值将观测插到规则网格点上是不够的。
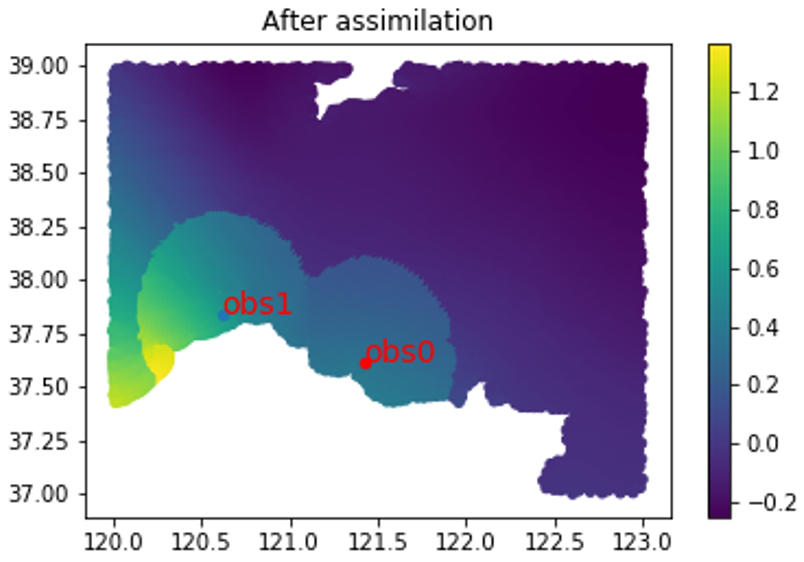
在资料丰富地区,来源于观测资料的信息占主导地位;而在资料稀少的地区预报会得益于先验的信息(背景场,第一猜测场),最早的先验信息是使用气候态的场,目前一般使用短期预报的结果做为格点的第一猜值。引入第一猜值的第一种方法SCM,是瑞典科学家Bergthorsson和Doos(1955)以及美国NWS的Cressman(1959)所发展的,引入背景场是资料同化历史上的一次重大思维突破,。①首先确定影响半径 ,影响半径范围内包含Ki个观测,为观测值。即在某点,它的值由该半径内的观测共同影响。②网格点的初始估计是由背景场给出,第一次估计以后,在由逐步订正引入观测:假定ἐ2=0,表明极度相信观测值;ἐ2>0,则假定观测本身是有误差的,同时给与背景场相应的权重。该公式表示,某点的值Ti由该点的背景场值+(系数1*观测增量1+系数1*观测增量1+...)/系数和。其中系数,Cressman(1959)定义的系数如下:其中,R表示影响半径;r表示测站与格点i的距离。表明观测资料对格点的订正只考虑距离该格点半径R内的那些测站。实例描述:如下图所示,白色部分表示陆地,彩色部分表示海洋已有的初猜值。现有两个观测点obs0和obs1的观测资料,利用逐步订正法将观测资料同化进去。运行后,发现观测资料已经被同化进背景场,对于观测站obs0,在影响半径内,都对背景场进行了调整,而两个观测站影响相交部分则由两个站共同决定。同样我们也发现了逐步订正法的优缺点,优点在于第一次引入了背景场和引入了观测增量,相对比较简单。缺点在于权重函数是经验给定的,给“密集区”观测和相对独立观测同样的权重是不合理。同样,对于观测较少的区域,例如obs0单独影响的区域,在边界地区也不够平滑。
import scipy.ioimport pandas as pdimport numpy as npimport matplotlib.pyplot as plt R=0.5
def findsite(x,y,latSite,lonSite): dis=np.sqrt(np.square(x-lonSite)+np.square(y-latSite)) mindis_index=np.argmin(dis) lon_site=x[mindis_index]; lat_site=y[mindis_index]; seri_index=np.where(x==lon_site)[0] return seri_indexback_file =scipy.io.loadmat(r'back_ground.mat')back_ground= back_file['back_ground']obs_file =scipy.io.loadmat(r'obs.mat')obs =obs_file['obs'] back_ground=pd.DataFrame(back_ground)back_ground.columns=['lon','lat','surge']obs=pd.DataFrame(obs)obs.columns=['lon','lat','obs'] dis0=np.sqrt(np.square(back_ground['lon']-obs['lon'][0])+np.square(back_ground['lat']-obs['lat'][0]))dis1=np.sqrt(np.square(back_ground['lon']-obs['lon'][1])+np.square(back_ground['lat']-obs['lat'][1]))back_ground['dis0']=dis0back_ground['dis1']=dis1 w0=(R**2-dis0**2)/(R**2+dis0**2)w1=(R**2-dis1**2)/(R**2+dis1**2) w0[w0<0]=0w1[w1<0]=0 obs_index0=findsite(back_ground['lon'],back_ground['lat'],obs['lat'][0],obs['lon'][0])obs_index1=findsite(back_ground['lon'],back_ground['lat'],obs['lat'][1],obs['lon'][1])background_obs0=back_ground.iloc[obs_index0]['surge'].valuesbackground_obs1=back_ground.iloc[obs_index1]['surge'].values back_ground['bluking0']=float(obs['obs'][0]-background_obs0)back_ground['bluking1']=float(obs['obs'][1]-background_obs1)back_ground['w0']=w0back_ground['w1']=w1back_ground['surge1']=back_ground['surge'] for i in range(0, len(back_ground)): if (back_ground.iloc[i]['w0']!=0) |(back_ground.iloc[i]['w1']!=0) : back_ground.loc[i,'surge1']=back_ground.iloc[i]['surge']+(((back_ground.iloc[i]['w0']*back_ground.iloc[i]['bluking0']+ back_ground.iloc[i]['w1']*back_ground.iloc[i]['bluking1']))/(back_ground.iloc[i]['w0']+back_ground.iloc[i]['w1']))plt.figure(0)plt.scatter(back_ground['lon'].values,back_ground['lat'].values,20,back_ground['surge'].values)plt.colorbar()plt.title('Assimilationbefore')plt.scatter(obs['lon'][0],obs['lat'][0],20)plt.text(obs['lon'][0],obs['lat'][0], 'obs0', fontdict={'size'
:14, 'color': 'red'})plt.scatter(obs['lon'][1],obs['lat'][1],20)plt.text(obs['lon'][1],obs['lat'][1], 'obs1', fontdict={'size':14, 'color': 'red'})plt.show() plt.figure(1)plt.scatter(back_ground['lon'].values,back_ground['lat'].values,20,back_ground['surge1'].values)plt.colorbar()plt.title('Afterassimilation')plt.scatter(obs['lon'][0],obs['lat'][0],20,'r')plt.text(obs['lon'][0],obs['lat'][0], 'obs0', fontdict={'size':14, 'color': 'red'})plt.scatter(obs['lon'][1],obs['lat'][1],20)plt.text(obs['lon'][1],obs['lat'][1], 'obs1', fontdict={'size':14, 'color': 'red'})plt.show()