引导(导向)滤波是由何恺明等人于2010年发表在ECCV的文章《Guided Image Filtering》中提出的,后续于2013年发表。引导过滤器根据局部线性模型原理,通过考虑引导图像的内容来计算过滤输出,引导图像可以是输入图像本身或另一个不同的图像。
论文链接:
引导滤波:
https://www.researchgate.net/publication/236228168_Guided_Image_Filtering
快速引导滤波:
https://arxiv.org/abs/1505.00996v1
github 链接:
https://github.com/Sundrops/fast-guided-filter
opencv文档:
https://docs.opencv.org/4.x/da/d17/group__ximgproc__filters.html#ga86813d59f8452a9600e979c6287805f5
三大保边滤波算法
保边滤波器 (Edge Preserving Filter)是指在滤波过程中能够有效的保留图像中的边缘信息的一类特殊滤波器。
三大保边滤波算法:
引导滤波:
双边滤波:https://users.soe.ucsc.edu/~manduchi/Papers/ICCV98.pdf
加权最小二乘平滑(WLS):论文是 Edge-Preserving Decompositions for Multi-Scale Tone and Detail Manipulation.
引导滤波(Guided Filtering)和双边滤波(BF)、最小二乘滤波(WLS)是三大边缘保持(Edge-perserving)滤波器。当然,引导滤波的功能不仅仅是边缘保持,只有当引导图是原图的时候,它就成了一个边缘保持滤波器。
还有一些保边平滑算法,比如1. 各向异性滤波, 2. 基于小波变换的滤波(Edge-avoiding wavelets and their applications), 3. 基于域变换的滤波(Domain Transform for Edge-Aware Image and Video Processing), 4. 基于 geodesic 的滤波(Geodesic Image and Video Editing) 等等。
论文摘要
在本文中,我们提出了一种新的显式图像滤波器,称为引导滤波器。从局部线性模型导出,引导滤波器通过考虑引导图像的内容来计算过滤输出,引导图像可以是输入图像本身或另一个不同的图像。引导过滤器也是一个比平滑更通用的概念:它可以将引导图像的结构传输到过滤输出,从而实现新的过滤应用,例如去雾和引导羽化。此外,无论内核大小和强度范围如何,引导滤波器自然具有快速且非近似的线性时间算法。目前,它是最快的边缘保留滤波器之一。实验表明,引导滤波器在各种计算机视觉和计算机图形应用中既有效又高效,包括边缘感知平滑、细节增强、HDR 压缩、图像抠图/羽化、去雾、联合上采样等等。
引导滤波简介
引导(导向)滤波顾名思义,就是有选择(导向)性的滤波,其与我们经常提及的高斯滤波、双边滤波相比,它具有导向性,说具体点就是,它通过输入一副图像(矩阵)作为导向图,这样滤波器就知道什么地方是边缘,这样就可以更好的保护边缘,最终达到在滤波的同时,保持边缘细节。所以有个说法是导向滤波是各向异性的滤波器,而高斯滤波、双边滤波这些是各向同性滤波器,我觉得也是很贴切。
引导滤波具有以下特点:
引导滤波器可以像流行的双边滤波器一样用作边缘保留平滑算子,但在边缘附近有更好的效果。引导过滤器也是平滑之外的一个更通用的概念:它可以将引导图像的结构传输到过滤输出,从而实现新的过滤应用,例如去雾和引导羽化。此外,无论核大小和强度范围如何,引导滤波器自然具有快速且非近似的线性时间算法。目前它是最快的边缘保留滤波器之一。
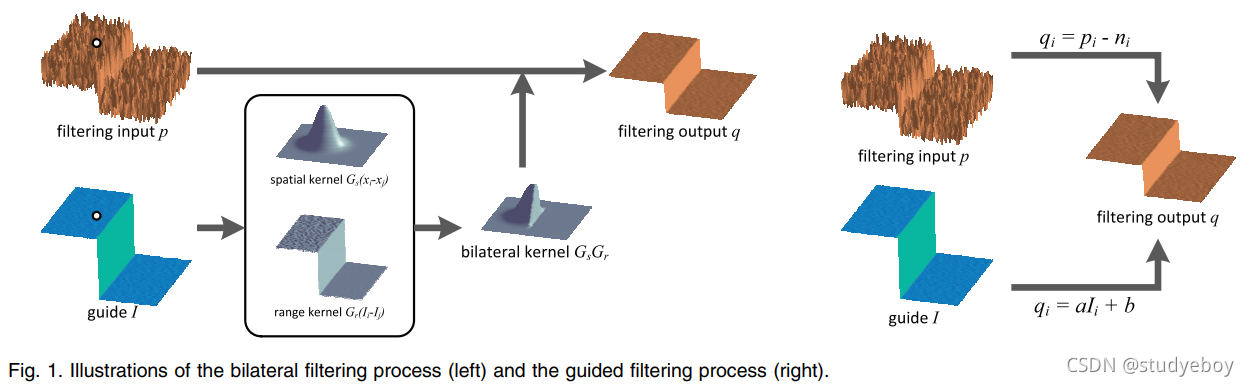
引导滤波(导向滤波)是一种图像滤波技术,通过一引导图像,对初始图像p(输入图像)进行滤波处理,使得最后的输出图像大体上与初始图像P相似,但是纹理部分与引导图相似。
引导滤波的前提条件是:
导引图像 与 输出图像 之间存在线性关系。
额外的数据(引导图像)可以指导滤波过程,得到更好(更适合)的去噪效果。

基于 opencv 实现代码
因为 opencv 的实现在扩展模块中,同时为了可以加深自己的理解,我们基于 opencv 部分常用算子实现了引导滤波的代码。
C++代码如下:
cv::Mat GuidedFilter(cv::Mat I, cv::Mat p, int r, double eps){ I.convertTo(I, CV_64FC1, 1.0 / 255); p.convertTo(p, CV_64FC1, 1.0 / 255);
int R = 2 * r + 1;
cv::Mat mean_I; cv::boxFilter(I, mean_I, CV_64FC1, cv::Size(R, R));
cv::Mat mean_p; cv::boxFilter(p, mean_p, CV_64FC1, cv::Size(R, R));
cv::Mat mean_Ip; cv::boxFilter(I.mul(p), mean_Ip, CV_64FC1, cv::Size(R, R));
cv::Mat cov_Ip = mean_Ip - mean_I.mul(mean_p);
cv::Mat mean_II; cv::boxFilter(I.mul(I), mean_II, CV_64FC1, cv::Size(R, R));
cv::Mat var_I = mean_II - mean_I.mul(mean_I);
cv::Mat a = cov_Ip / (var_I + eps);
cv::Mat b = mean_p - a.mul(mean_I);
cv::Mat mean_a; cv::boxFilter(a, mean_a, CV_64FC1, cv::Size(R, R));
cv::Mat mean_b; cv::boxFilter(b, mean_b, CV_64FC1, cv::Size(R, R));
cv::Mat q = mean_a.mul(I) + mean_b; q.convertTo(q, CV_8UC1, 255);
return q;}
python代码如下:
def guided_filter(I, P, r, eps): scale = 255 I = I/scale P = P/scale
R = 2*r+1
P_mean = cv.boxFilter(I, -1, (R, R)) I_mean = cv.boxFilter(P, -1, (R, R))
I_square_mean = cv.boxFilter(np.multiply( P, P), -1, (R, R)) I_mul_P_mean = cv.boxFilter(np.multiply( I, P), -1, (R, R))
var_I = I_square_mean-np.multiply(I_mean, I_mean) cov_I_P = I_mul_P_mean-np.multiply(I_mean, P_mean)
a = cov_I_P/(var_I+eps) b = P_mean-np.multiply(a, I_mean)
a_mean = cv.boxFilter(a, -1, (R, R)) b_mean = cv.boxFilter(b, -1, (R, R))
dst = np.multiply(a_mean, P)+b_mean
dst *= scale return dst
效果展示
在这里,我们暂时只研究引导 I 与过滤输入 P 相同的特殊情况。

计算量
引导滤波算法快的关键之处在于计算a_k,b_k所需的均值与方差都可以通过盒式滤波去实现,盒式滤波是一种与滤波半径大小无关的算法,其实现方法类似积分图思想,都是一种以空间换取时间的方式。因为相邻像素之间有许多重复计算的地方,这些地方可以暂时记录下来,后面需要用到时直接读取就行了。
快速引导滤波算法
导向滤波的时间复杂度为O(N),其中N为像素点的个数。
何凯明在2015又发表了一篇《Fast Guided Filter》的文章,阐述了一种很实用的更快速的导向滤波流程。如下所示。其本质是通过下采样减少像素点,计算mean_a & mean_b后进行上采样恢复到原有的尺寸大小。假设缩放比例为s,那么缩小后像素点的个数为N/s^2,那么时间复杂度变为O(N/s^2)(注意,上下采样也需要消耗一部分算力)。

基于上面的理论,只需调用 resize() 函数就可以实现下采样和上采样了
总结
在本文中,我们提出了一种广泛适用于计算机视觉和图形的新型过滤器。与最近加速双边滤波器的趋势不同,我们设计了一种新的滤波器,它展示了边缘保留平滑的良好特性,但可以计算有效地和非近似地。我们的过滤器比“平滑”更通用,适用于结构转移,实现基于过滤的羽化/消光和去雾的新应用。由于局部线性模型是一种无监督学习,因此可能会应用其他高级模型/特征来获得新的过滤器。我们将其留作将来的研究。
更多详细介绍可以参考原论文。
参考文献
https://codeantenna.com/a/VVFmrqhEQq
https://blog.csdn.net/studyeboy/article/details/121137028
https://blog.csdn.net/cyh706510441/article/details/49467191
- 机器学习交流qq群955171419,加入微信群请扫码
