计算机相关概念太难、太抽象?别怕,往下看!
人类对视觉信息的记忆要远远大于文字信息。使用图表等形式的可视化,可以让抽象、难懂的概念一目了然;在此基础之上,添加可控的参数调节器,将更有助于对概念的深入学习与理解。
马尔科夫链
马尔科夫链是指数学中具有马尔科夫性质的离散事件随机过程。在其每一步中,系统根据概率分布可以从一个状态变到另一个状态,也可以保持当前状态。状态的改变叫做转移,与不同的状态改变相关的概率叫做转移概率。
这概念是不是看着有点晕?没关系,我们来看下面这张图:
 2种状态的马尔科夫链
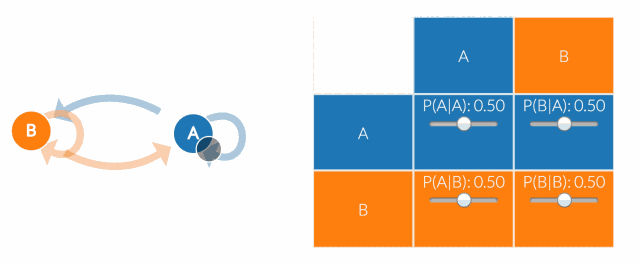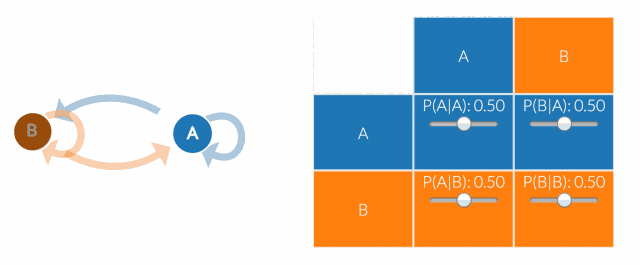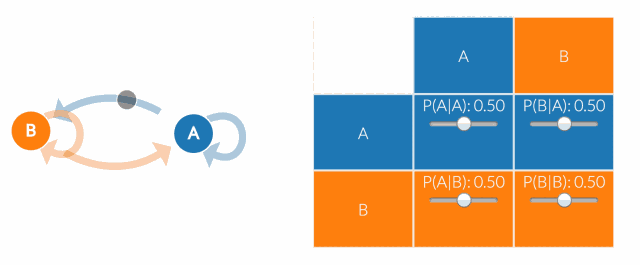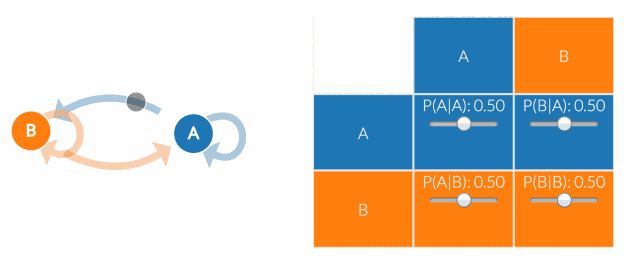
2种状态的马尔科夫链在状态空间中有两种状态,A和B。共有4种可能的转换。如果我们在A,接下来可以过渡到B或留在A。如果我们在B,可以过渡到A或者留在B。在这张图中,从任意状态到任意状态的转移概率是0.5。
当然,真正的建模工作者不会总是就画一张马尔科夫链图。相反,他们会使用“转移矩阵”来计算转移概率。状态空间中的每个状态都会出现在表格中的一列或者一行中。矩阵中的每个单元格都告诉你从行状态转换到列状态的概率。因此,在矩阵中,单元格做的工作和图中的箭头所示是一样。
如果状态空间添加了一个状态,我们将添加一行和一列,向每个现有的列和行添加一个单元格。这意味着当我们向马尔可夫链添加状态时,单元格的数量会呈二次方增长。因此,转换矩阵就起到了很大的作用(除非你想把法尔科夫链图画的跟丛林一样)。
马尔科夫链的一个作用是用计算机模拟现实世界中的现象。例如,可以用来检测一个新建的水坝溢流的频率(取决于连续下雨的天数)。为建立这个模型,可以从下面的雨天(R)和晴天(S)开始:
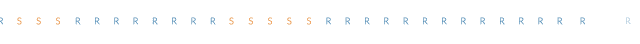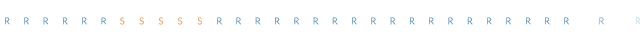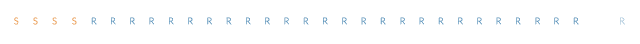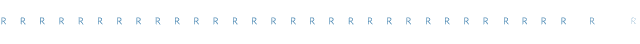
表述这种模拟天气的方法就是:“有一半的天数是下雨天。所以模拟中的每一天都有50%的概率是下雨的。”这个规则在模拟中所产生的序列如下:
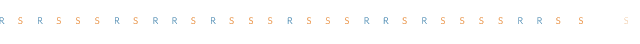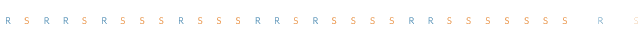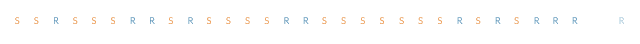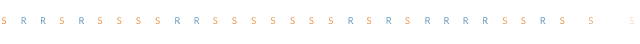
你注意到上面的序列和原来的不太一样了吗?第二个序列似乎具有跳跃性,而第一个(真实数据)似乎具有“粘性”。在真实的数据中,如果某一天是晴天,那么第二天也很可能是晴天。
可以通过两个状态的马尔可夫链来消除这种“粘性”。当马尔科夫链处于状态“R”时,它保持在该状态的概率是0.9,状态改变的概率是0.1。同样,“S”状态保持不变的概率是0.9,过渡到“R”状态的概率是0.1。
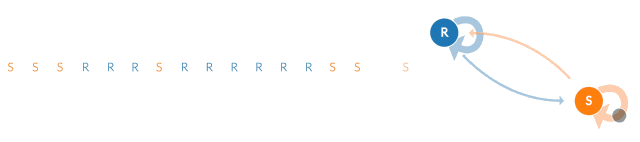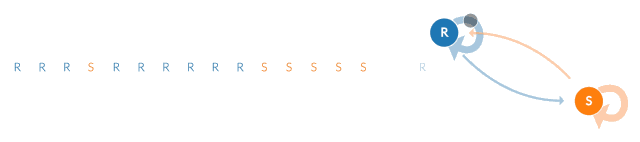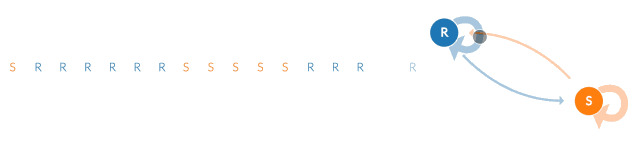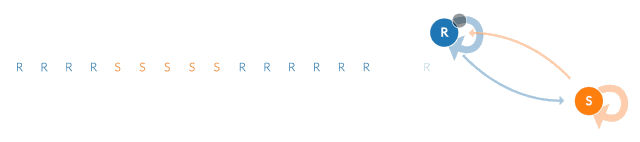
在许多需要对大规模的现象做研究的工作人员手中,马尔科夫链的作用可以变得非常强大。例如,谷歌用于确定搜索结果顺序的算法,称为PageRank,就是一种马尔可夫链。
主成分分析(PCA)
主成分分析,是一种统计方法。通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量,转换后的这组变量叫主成分。PCA是最重要的降维方法之一,在数据压缩消除冗余和数据噪音消除等领域都有广泛的应用。
2D示例
首先,只考虑两个维度的数据集,比如高度和重量。这个数据集可以绘制成平面上的点。但如果想要整理出变量,PCA会找到一个新的坐标系,其中每个点都有一个新的(x,y)值。坐标轴实际上没有任何物理意义。它们是高度和重量的组合,被称为“主分量”。
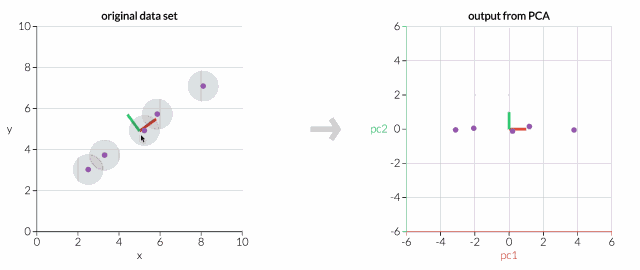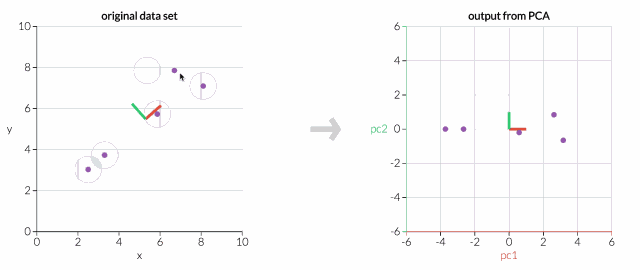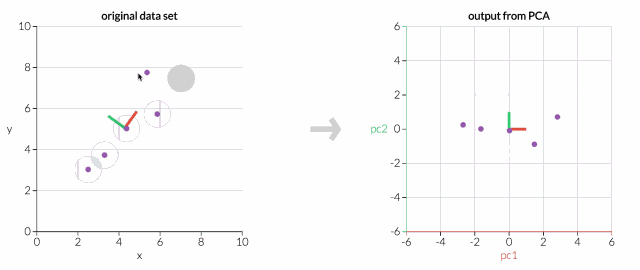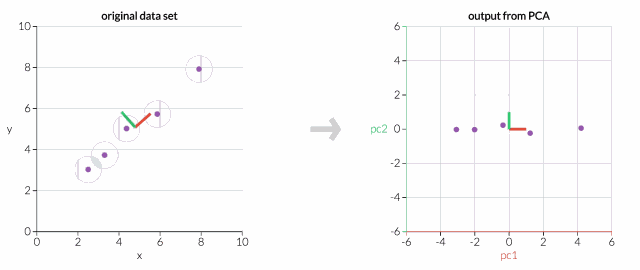
拖动原始数据集中的点,可以看到PC坐标系统正在调整
PCA对于降维很有用。下面,我们将数据绘制成两条直线:一条由x值组成,另一条由y值组成。
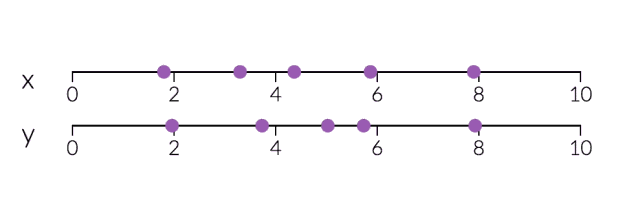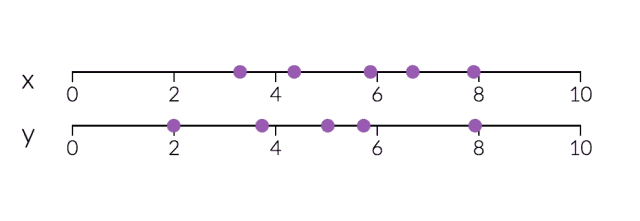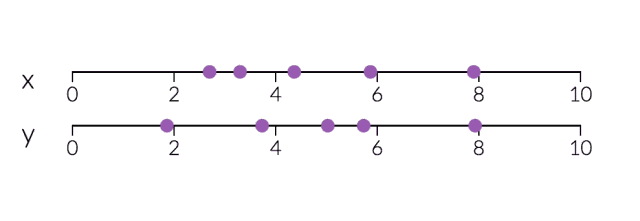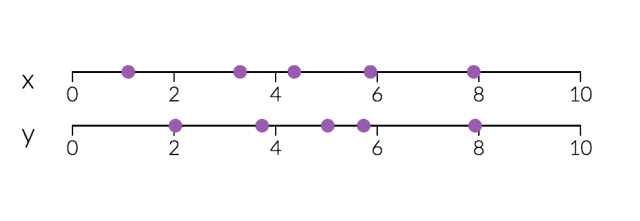
但是,如果我们只打算沿一个维度查看数据,那么将该维度作为具有最大变化的主成分可能会更好。通过减少PC2,不会造成太大损失,因为它对数据集的变化贡献最小。
3D示例
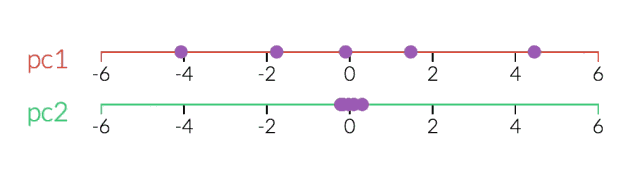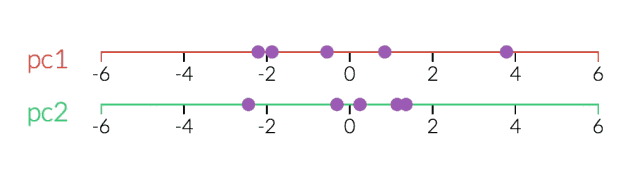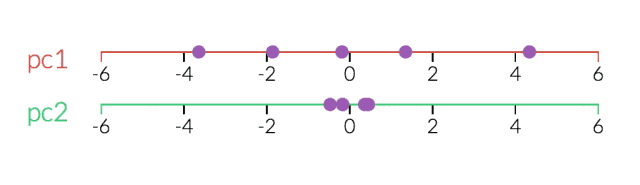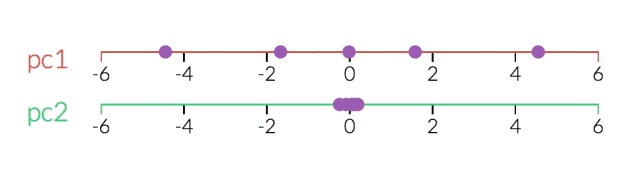
看透一个数据云是非常困难的,因此,在3D空间中,PCA显得更为重要。在下面的示例中,原始数据以3D的形式绘制,但可以通过不同的视角,将其投射到2D空间。确定好角度之后,点击“显示PCA”按钮,即可呈现2D的结果。在本例中,PCA变换确保水平轴PC1的变化量最大,垂直轴PC2的变化量次之,第三轴PC3的变化量最少。显然,PC3是丢弃的。
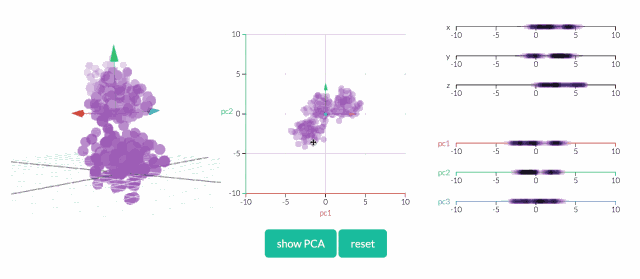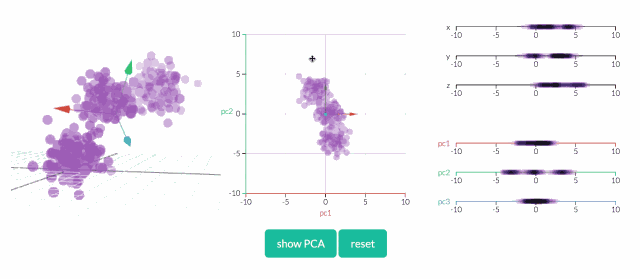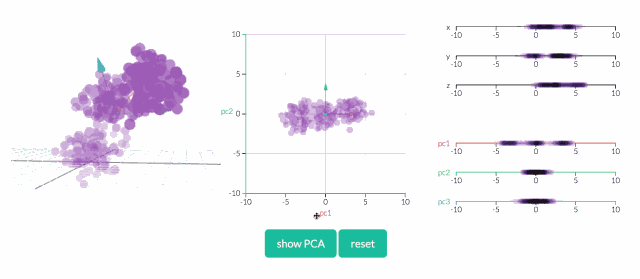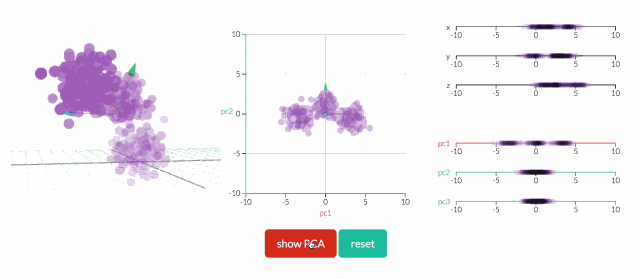
应用:吃喝在英国
如果数据集不仅仅是三维的,而是17个维度的呢?!如下表所示:
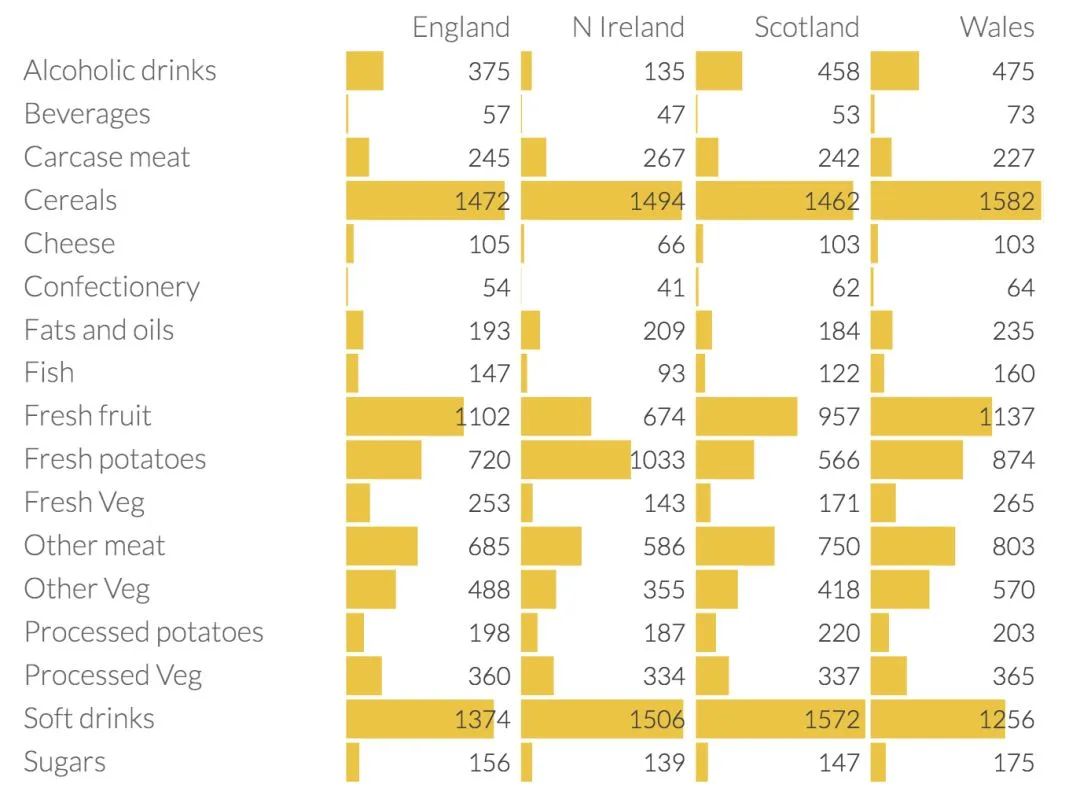
表中是英国每个地区平均每人每周17种食物的消费量,单位为克。这张表显示了不同食物类型之间存在的一些有趣的差异,但总体差异并不显著。让我们看看PCA是否可以通过降维来强地区家之间的差异。
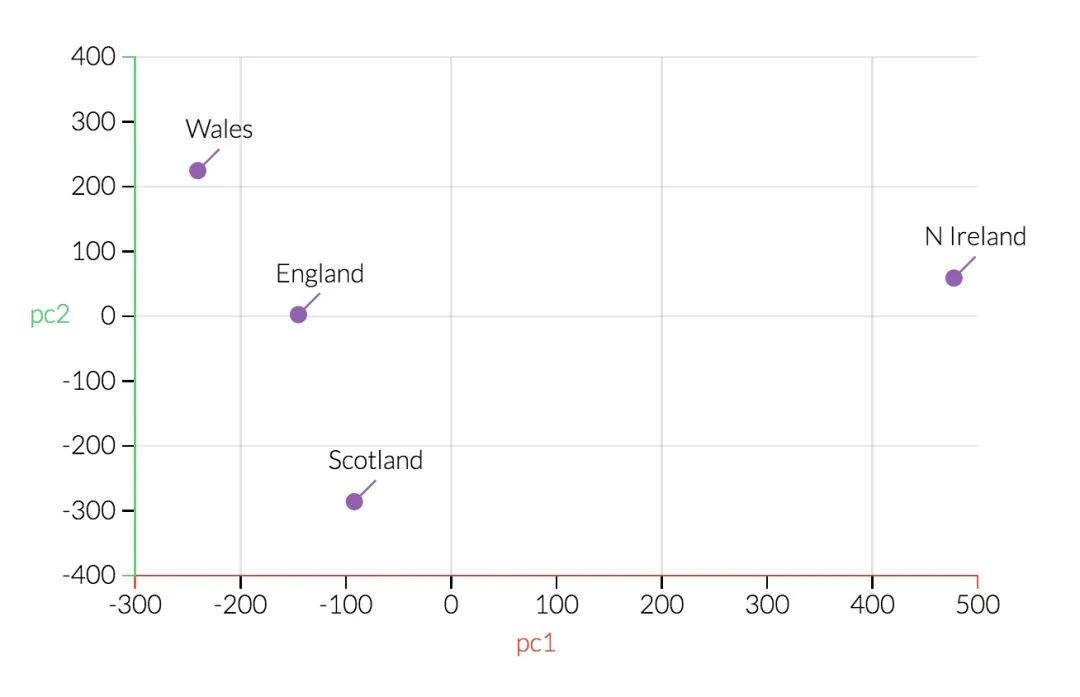
下图是第一个主成分的数据图。我们可以看到一些有关北爱尔兰的情况已经发生了变化。

现在,看看第一和第二主成分,可以看到北爱尔兰是一个主要的异常值。一旦回过头来看看表格中的数据,这就显得很有道理了:北爱尔兰人吃的新鲜土豆要很多,吃的新鲜水果、奶酪、鱼和酒精饮料较少。这是一个很好的迹象,我们所看到的结构反映了现实世界地理的一个重要事实北爱尔兰是四个国家中唯一一个不在大不列颠岛上的。
条件概率
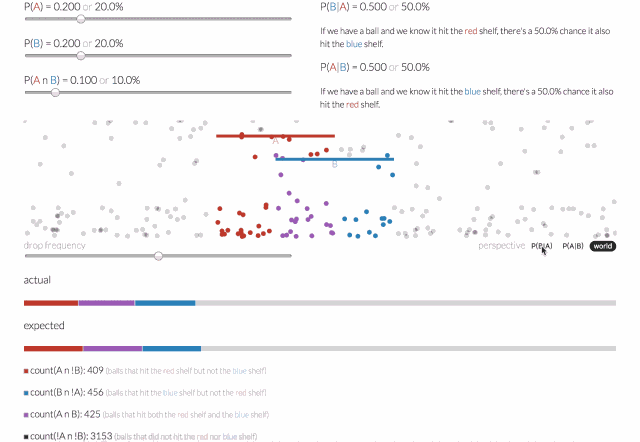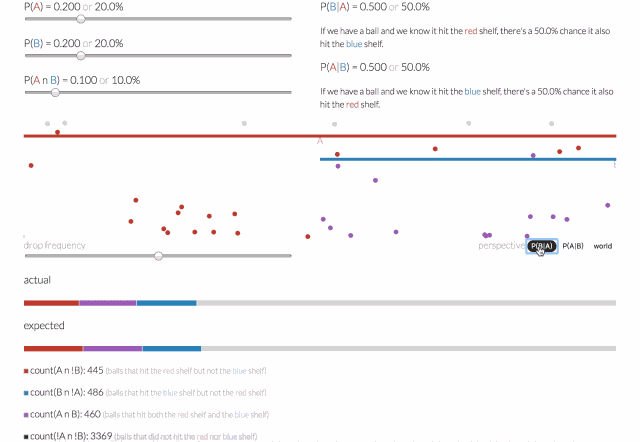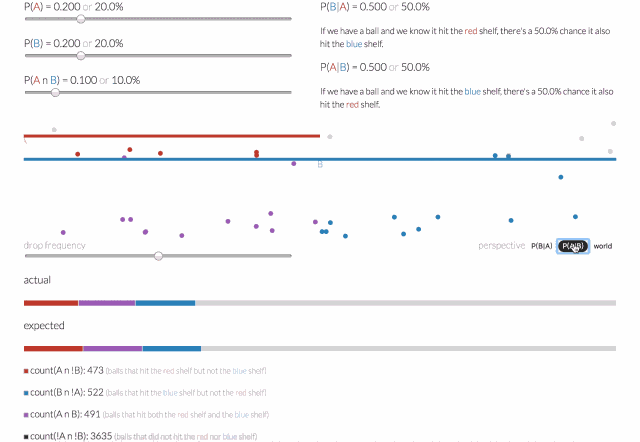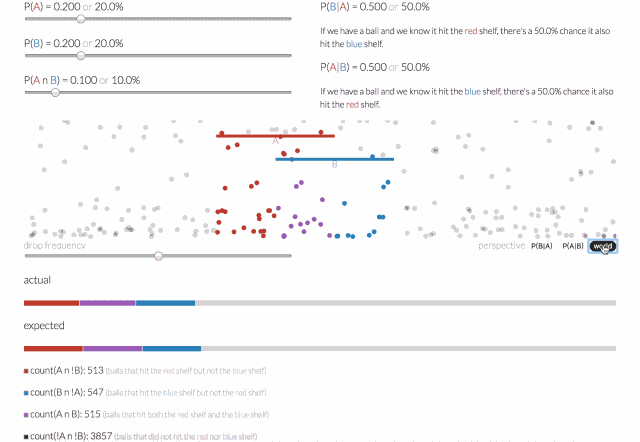
条件概率是指一个事件在另外一个事件已经发生条件下的发生概率。一个落下来的球可能落在红色的架子上(称之为A事件),或者落在蓝色架子上(称之为B事件),或者两者兼而有之。
那么给定一个球,它击中了红色架子(A事件),而后击中蓝色架子(B事件)的概率会是多少呢?可以通过给定A的条件概率,即P(B | A)来回答这个问题。
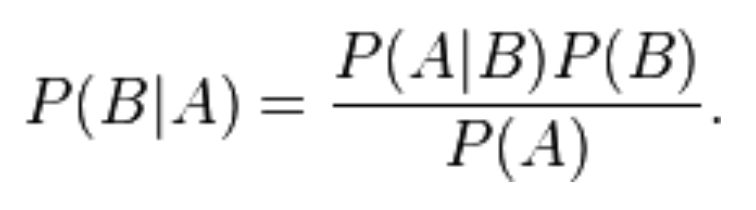
将抽象、难懂的计算机概念,以可视化的形式展现出来,可以帮助学生、研究者更好的理解;甚至可以帮助教师们提高教学质量。
无论如何,希望读者们能从本文中得到或多或少的帮助。
-
机器学习交流qq群955171419,加入微信群请扫码
