TOC: Infinite Physical Monkey.
利用AI方法解决科学问题已经成为一种趋势,然而在其火热发展的进程当中也有很多人质疑其有效性。碳硅智慧的张昊天,张锦途,赵慧峰等研究者刚发布了一篇论文,该论文针对最近发表的论文“Do Deep Learning Methods Really Perform Better in Molecular Conformation Generation?”当中的证明方法提出质疑,并阐述了自己在构象生成任务上的观点。
(Zhou, Gengmo, Zhifeng Gao, Zhewei Wei, Hang Zheng, and Guolin Ke. "Do Deep Learning Methods Really Perform Better in Molecular Conformation Generation?." arXiv preprint arXiv:2302.07061 (2023).
https://doi.org/10.1101/2023.03.08.531607)
构象生成是计算机辅助药物设计和化学信息学的一个基本问题。一般来说,它可以根据分子的大小分为三个尺度,即小(有机物)、中(纳米颗粒状)和大(蛋白质和核酸)三个尺度。与药物设计最相关的是小尺度有机分子构象的生成,主要包括在真空和蛋白质口袋环境中生成化合物的优势构象。最近,随着几何神经网络的发展,一系列深度学习方法成功应用于真空中和蛋白口袋环境中小分子构象的生成。前者(真空中)在各种基线实验中击败了传统的基于距离几何的ETKDG方法,后者(蛋白口袋环境中)则追平了主流的分子对接软件。在这些方法展现出了强大性能的同时,最近一些研究人员声称{Zhou, 2023 #536},这些深度学习方法被一种 "无参数"的方法所击败。值得注意的是,他们在文中所提出的无参数方法与著名的无限猴子定理类似,只不过他们的猴子接受过物理教育,带有更强的物理知识。为了讨论他们证明的合理性,本文构建了一个真正的无限随机猴子方法用于分子构象生成,进而证明了这种更加随机的方法在测试集上的COV指标也同样高于大多数深度学习模型。除此之外,作者还将他们的无限物理猴子扩展到蛋白口袋内小分子结合构象的预测问题上,发现了这种物理猴子即使在更难的对接构象预测问题当中仍然表现出极优的性能。因此,虽然作者赞同他们在原文当中的部分结论,但是他们的证明过程的合理性也许需要进一步的讨论。
除了评估他们的算法和结论的合理性外,无限物理猴子还启发作者:对于对接姿势的生成,深度学习模型真正学习了残基和配体之间的相互作用规律。在本文最后还发现了隐藏在口袋给定对接问题的训练中的归纳偏置,并且提出了一个简单易行的解决方案。相关算法的代码可以在以下网址找到:
https://github.com/HaotianZhangAI4Science/infinite-physical-monkey.
结合构象的预测是药物发现和化学信息学中的一个基本和重要的问题,其目的是获得蛋白质口袋和候选药物之间的位置和朝向关系。一旦结合构象确定好,药物研究者就可以利用这种蛋白质-配体之间的相互作用信息进行基于结构的(SBDD)和基于配体的药物设计(LBDD)。尤其是在SBDD当中最流行的高通量虚拟筛选中,蛋白-配体的结合构象对所筛选的化合物库中每个分子的结合能计算起到决定性的作用。基于虚拟筛选的方法假阳性率高的重要原因之一就是对结合构象的预测不够准确。
目前已经有很多预测结合构象的算法,其中一些经典的方法已经被广泛地应用于虚拟筛选当中。从采样策略上来讲,结合构象算法可以分为系统搜索、启发式搜索和确定性搜索。以Glide为代表的系统搜索法对所有自由度进行搜索采样,这种系统搜索法虽然可以搜到全局极小值,但是采样复杂度随着可旋转键的数量呈指数级增长。因此,在实际应用中为了克服维度灾难问题,一般要事先根据经验规则进行过滤,缩小潜在的搜索空间。启发式搜索方法对配体构象进行随机变换,然后由评价函数接受或拒绝以更新构象。这个过程反复进行直到收敛。启发式搜索方法的代表有利用遗传算法的AutoDock和利用模拟退火算法的LeDock。确定性搜索算法则以分子动力学为引擎,用贪婪的策略探索构象空间,一步步向低能量区域移动。然而,由于确定性搜索会在相同的初始状态和相同的动力学参数下坍缩到相同的最终状态,所以在应用当中它并不怎么常见。具有代表性的确定性搜索软件有基于CHARMM分子动力学模拟软件的CDOCKER。尽管在过去的几十年当中,这些分子对接算法在药物发现中起到了一定的作用,但由于蛋白质-配体相互作用的内在复杂性,加上难以计算的熵效应和溶剂效应,结合构象预测问题仍然远远没有达到让人满意的地步。
近年来,研究者开始尝试采用数据驱动的方式来解决结合构象预测问题。DeepDock遵循启发式搜索的思路,利用图神经网络训练了一个评分函数来接受和拒绝构象。EquiBind提出了一个SE(3)等变网络,利用等变性约束直接预测配体在口袋内的笛卡尔坐标。TankBind则利用三角注意力机制生成二维结构信息,即配体内部和配体原子与蛋白质原子之间的原子间距离,进而恢复三维构象。然而,二维距离矩阵到三维构象的转换并不一一映射,因此三维重构的过程会进一步损害结合构象预测的准确性。因此,利用二维到三维转换的几何预测方法的模型需要将直接获得的构象进行弛豫。DiffDock则利用扩散模型在内坐标空间上进行旋转,平移和二面角空间进行采样生成构象。这种更“物理”的策略使得DiffDock在对接构象预测上达到了SOTA效果。基于深度学习的结合构象预测模型的快速发展的基础来源于小分子构象生成方法,如直接生成笛卡尔坐标的GeoDiff,从二维距离矩阵重构三维坐标的CGCF和SDEGen,以及在扭转空间进行生成的Torsional Diffusion。
最近,有一项研究显示1,基于深度学习的构象生成模型并不一定优于无参数方法。该研究利用RDKit中的EDKDG算法采样2000个构象,然后从中取出1/6的构象随机旋转二面角,取出1/6构象作力场优化,最后将这些构象叠合在原点并根据三维坐标进行聚类。他们构建的基线模型在COV和MAT指标上追平了深度学习的方法。因为这种无参数模型可以取得SOTA结果,因此他们质疑了深度学习构象生成方法中评测指标的合理性。需要指出的地方有两点:第一,针对分子构象生成问题,COV和MAT指标的计算仅仅是模型评测的一部分。其在文章中的“By revising the MCG setting in many deep learning based methods, we suggest the community rethink the benchmark in the current MCG, and focus on the end applications in various MCG-related downstream applications in the future.”但是构象生成的评测方法不止文章中提到的COV/MAT这么一种。如GraphDG, ConfGF,GeoDiff等文章当中比较了生成构象系综的和原始数据集当中的量化计算系综的热力学性质之差;DMCG当中证明了利用模型生成的构象作下游对接任务时,对接成功率得到了提升;SDEGen当中不仅和晶体构象作了比较,而且还做了动力学采样出分子的势能面,将模型生成的构象和RDKit生成的构象在势能面上做定性地比较。表一列出了分子构象生成领域中各个模型所涉及到的评测方法,这篇评述的作者选择性地忽视了除了COV/MAT以外的其他指标。第二,他们构建的无参数化方法之所以能击败其他机器学习模型,是因为采样量过大,这和无限猴子定理不谋而合,而且还是受过物理教育的猴子(RDKit产生构象的算法并不是一个纯随机的方法)。因此,作者在本文中构建了一个真正的无穷随机猴子算法用于说明即使这种更随机的方法也可以达到他们报导的精度。与他们的无穷物理猴子相比,无限随机猴子更进一步地摆脱了对ETKDG算法参数的依赖,这个方法的思路如下:作者对化学键采用谐振子模型建模,在这种条件下,键长分布可以用高斯分布很好地逼近。作者统计数据集当中不同键类型(如碳碳单键,碳氧双键)的键长平均值和标准差以拟合每一种化学键的分布。在生成构象过程当中,对每一个化学键长依据统计的高斯分布重采样,然后根据键长的二维信息重构分子的三维构象。实验表明无穷随机猴子几乎取得了和他们所提出的无限物理猴子(RDKit+Clustering)算法接近的效果,进一步说明了他们论文中比较方法的不公平性。至少,他们还应该为深度学习方法取样2000个构象,然后再进行聚类。
作者将Zhou et al.1的无穷物理猴子推广到了结合构象预测问题中,并且构建了考虑口袋信息的Scoring和基于力场优化的UFF基线模型。作者的方法强调了大采样量对于提高分子对接成功率的重要性,对使用RDKit+Clustering作为基线模型的公平性提出怀疑。此外,作者表明无穷物理猴子模型还可以作为对接构象生成的随机基线。表6当中列出了Uni-Dock方法,两种传统对接方法,两种给定口袋的深度学习方法以及作者构建的基线模型的对接成功率。从中作者得出两点结论:1. 从给定口袋的对接成功率上讲,机器学习模型有机会超越传统模型。2. 任何基于深度学习的对接模型的表现都必须超过无穷物理猴子才可以证明模型的基本有效性。除此之外,作者还指出当前基于口袋的对接模型可能存在的归纳偏置,并且指出了简单易行地克服该偏置的训练方法。
如前所述, RDKit+Clustering的策略本质上就是无穷猴子定理的物理版本,犹如用机关枪打靶然后聚类取分数一样。在采样相同样本量的情况下,COV/MAT可以部分反映构象系综的质量。为了进一步证明在大样本量下,随机算法同样可以达到SOTA的效果,作者设计了一个真正的无参数化随机方法,即无限随机猴子(Infinite Stochastic Monkey)。如图1所示,这个算法如下:1)随机采样器,作者首先统计数据集当中不同类型化学键的键长分布,并且基于谐振子模型假设对键长分布进行高斯逼近,通过键长构建分子的伪距离矩阵,并以此出发重构分子的三维构象;2)ETKDG约束的二面角随机采样器,作者利用ETKDG算法产生一系列构象,接着在分子的二面角空间进行随机采样,产生键长键角分布,满足ETKDG算法分布,但是二面角分布是均匀随机分布的构象。3)力场优化采样器,对1)产生的随机构象进行MMFF力场优化,获得以随机构象为起始点的力场优化后的构象。与RDKit+Clustering相比,作者的方法进一步摆脱了对先验知识的依赖,采样速度提高~10倍左右。测试时生成的样本量作者也采用与原文一致的采样量 ,即
,即
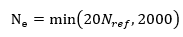
其中 是集合中所测试分子所对应的量化精度下的优势构象数目,二面角随机构象数和力场优化构象数是随机构象数的1/4。同样的,作者也利用K-means算法聚类两倍于的构象,取每一类的中心作为伪构象进行评测。
是集合中所测试分子所对应的量化精度下的优势构象数目,二面角随机构象数和力场优化构象数是随机构象数的1/4。同样的,作者也利用K-means算法聚类两倍于的构象,取每一类的中心作为伪构象进行评测。
图一:无限物理猴子算法在结合位姿预测问题上的工作流
无限物理猴子除了在分子构象生成问题上可以取得极高的性能外,在结合构象生成问题上,其也可以达到类似的结果。在药物设计应用当中,最常采用的方案是给定蛋白口袋的结合构象预测(一个更有名的说法是分子对接)。作者将Zhou et al.1 的无限物理猴子算法推广至对接构象预测问题当中,算法如下:1)利用ETKDG算法产生分子构象,此时的构象生成没有考虑任何的蛋白环境。2)将分子放置到口袋的几何中点上,然后以几何中点为中心进行随机旋转,获得最后的基于无穷物理猴子的对接构象。除此之外,作者还提出了一个考虑口袋内化学环境的scoring基线模型,即获得基于无穷物理猴子的对接构象之后,利用Vina打分评估该构象和口袋的结合能,按照结合能从低到高的顺序对分子进行排序。除了这种后处理式的考量口袋内化学环境的方法,作者还提出了一个基于力场的结合构象预测基线:在口袋残基固定的情况下以无穷物理猴子构象为起始点对构象进行力场优化以获得结合构象。通过评测在分子构象生成任务上和结合构象预测任务上的无穷物理猴子算法,作者得出这样的结论:较大的采样量会使与RMSD相关的指标持续提升。因此作者对文中1所采用的比较方法提出一些建议:当使用RDKit的无限猴子时,也应该和让其他机器学习方法成为无穷猴子。尽管作者部分赞同COV/MAT并不是一个完美的指标,但是世间并不完美。如果把一种方法比作一头大象,那么每一种指标就像一个摸象的盲人一样,只有采用不同的指标进行评测才能尽可能地了解这头大象的整体形貌。遗憾的是,他们只询问了一个正在摸大象腿的盲人,这个大象究竟是什么样子,而忽视了其他盲人的看法?。
作者赞同Yu et al.2的结论:深度对接模型应该更关注于局部对接的情况,即预测给定口袋情况下小分子的结合构象。尽管目前的深度对接模型大部分是在整个蛋白质上进行全局对接,如DiffDock, EquiBind等,但要公平地比较不同模型的性能,仍需在相同条件下进行对接评测。因此,作者最后比较了在给定口袋的情况下,深度学习模型,传统模型,随机模型之间的对接性能,包括AutoDock GPU,Glide SP,Uni-Dock,LigPose,TankBind以及本文构建的三种基线模型。其中成功对接定义为top-1构象和晶体构象的RMSD<2Å。
表二. 不同方法在GEOM-QM9和GEOM-Drugs上的表现
虽然本文提出的无限随机猴子算法比RDKit+Clustering策略更加随机,但在COV/MAT指标上仍取得了与SOTA相似的效果,进一步说明了纯随机算法在进行大量构象采样的情况下可以取得极高的COV/MAT指标。不难理解,当进行大量构象采样时,等于对分子的构象空间进行了均匀的采样。相当于把无限的猴子随机扔到分子的势能面上,然后分析这些猴子在势能面上的覆盖率。这种随机方法的结果是自然的:大样本量下采样的构象几乎会覆盖到势能面上的所有区域,这其中就包括量化计算得到的低能参考构象。而以RDKit所产生的构象作为起点,这些在势能面上的猴子进一步受到物理规则的驱动,更容易走到势能面上相对较低的区域。因此,如表二所示,在一个相对较大而不是无限的采样量下,物理猴子比随机猴子对低能构象的覆盖率要更高。
另一方面,深度学习方法在较小的采样量下可以更好的覆盖到低能构象空间。因此,在大量采样的情况下,Zhou and Yu等怀疑深度学习分子构象生成模型无法优于RDKit+Clustering的结论值得商榷。更重要的是,如上所述,由于COV/MAT指标存在局限性,大部分深度学习分子生成方法的评价并非单一地依赖于这两个指标。因此,对于分子构象生成方法,仅基于COV/MAT指标的性能评价缺乏意义。
表三. 无限物理猴子在不同阈值和采样数下的命中率
为了进一步说明采样量对势能面覆盖率的影响,本文将无限物理猴子算法扩展到了结合构象预测问题上。表三展示了无限物理猴子算法在不同大小构象集合和不同RMSD阈值下的表现。对于2000个构象集合,2埃以内的成功率高到74.84%,几乎优于大部分传统方法,但是这些构象并不可能用于下游任务。这与RDKit+Clustering中的讨论类似。似乎按照Zhou1的观点来看,由于随机猴子算法产生的结合构象几乎不可能为有效构象,所以应该是对接构象的benchmark有问题。但事实上,离开样本量谈命中率是不正确的。如果看top-1,top-5的命中率的话,基本就和作者的预期相符,无穷物理猴子的命中率是极低的。
图二:三种基于无限物理猴子的基线模型在不同阈值下的对接成功率
进一步挖掘无穷物理猴子算法带来的启示。作者计算随机构象在口袋内的结合能,依据这个结合能排序计算随机构象和晶体构象之间的RMSD,对应的结果在表4当中。可以发现,新计算的top-1, top-5的2埃成功率相较于之前的无限物理猴子算法略有提高,这是因为在计算结合能进行排序的过程中,更合理的结合构象(拥有较低的结合能)被排到前面。由于这些构象均基于随机旋转所产生,即使部分构象与晶体构象之间具有较低的RMSD,它们在能量上并不具备优势,甚至有些构象会与蛋白口袋内的残基发生碰撞。这一实验进一步说明了无穷物理猴子模型的随机性。但在相同的采样量的情况下(top-1和top-5),对接成功率依然是一个有效的评测指标。
另一个有趣的问题是在进行物理规律的指导下(力场优化),离散分布在势能面上的随机构象,是否可以进一步优化到低能构象,进而提高对接成功率。力场指导下的几何优化可以驱使分子构象移动到最近的局部势能低点中,所以优化后的几何构象不仅取决于所选取的力场,也取决于分子的初始结构。从表6可以看出,与随机构象相比,其2埃内top-1命中率从1.76%上升到了9.23%,top-5命中率上升到了26.66%,图2展示了三种方法在1,5和2000构象采样量下的命中率。从这个图当中可以得出以下两个结论:
1. 任何机器学习模型如果成功学习了口袋内分子构象的分布规律,那么对接成功率指标应当优于无穷物理猴子模型。从目前报导的模型来看,深度学习模型毫无疑问地超过了无穷物理猴子模型,证明了这些模型的有效性。
2. 在利用深度学习开发结合构象预测模型时(即对接软件),更应关注局部对接情况,且在训练模型时要注意切分口袋时存在的归纳偏置。如果输入的口袋均以晶体构象的几何中心进行切割,这样会导致模型只见过位于口袋中心的构象,冻结预测结合构象时的平移自由度。一个简单地改进方案就是在切口袋的时候对晶体构象的几何中心?加一个高斯噪声扰动,即
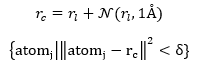
其中 为配体构象的几何中心,
为配体构象的几何中心, 即为欲切口袋的几何中心,
即为欲切口袋的几何中心,
 为口袋的原子,
为口袋的原子,
 为给定切口袋的阈值。
为给定切口袋的阈值。
表六中比较了局部对接情况下传统对接方法与深度学习方法的对接成功率。为公平起见,作者选取了两个传统方法(AutoDock,Glide SP),两个深度学习方法以及作者构建的三个baseline。如图所示,在局部对接情况下,传统方法可以达到66.8%的精度(Gilde SP),而基于深度学习的LigPose则取得了SOTA的效果(74.7%),这说明了在给定口袋的条件下,深度学习方法优于传统方法。另一种方法TankBind虽然只取得了24.2%的精度,但是仍然远高于本文构建的基于UFF力场的口袋优化baseline和无限物理猴子和Scoring的随机baseline。,本文作者认为,只要深度学习对接方法超过无限物理猴子模型或者是Scoring方法(最好是Top-5的表现),即可证明该方法学到了口袋残基和配体之间的相互作用规律。总之,深度学习在结合构象预测方面确实有机会超过传统方法,而对于这两类方法,衡量其有效性的最终方法是通过后续的生物活性实验。
这篇文章当中,作者系统地分析了无限物理猴子算法在分子构象生成和结合预测方面作为基线模型的合理性,得到了如下的结论:
虽然COV/MAT有其自身的局限性,但RDKIt+Clustering之所以优于其他基于深度学习的模型的原因主要是过高的采样量。而且在分子生成领域,还有多角度的构象生成质量的评价指标,单纯地运用COV/MAT作为评测是极其不合理的。
在结合构象的预测当中,无限物理猴子算法可以作为一个随机基线模型用于证明方法的有效性。
作者在给定口袋下的公平比较中表明深度学习方法确实可以增强结合构象预测问题。此外,这种比较揭示了在数据处理过程中隐藏在口袋截断过程中的归纳性偏差。
总之,作者的分析表明,使用基于物理学的指标和考虑样本量是评价分子构象生成和结合姿势预测方法性能的重要因素。作者的结果强调了基于深度学习方法的潜力和在数据处理阶段考虑归纳偏差的重要性。
作者感谢宋剑飞和施慧,以及碳硅智慧的全体正式员工为本工作提供的帮助。
Zhou, G., Gao, Z., Wei, Z., Zheng, H. & Ke, G. Do Deep Learning Methods Really Perform Better in Molecular Conformation Generation? arXiv preprint arXiv:2302.07061 (2023).
Yu, Y., Lu, S., Gao, Z., Zheng, H. & Ke, G. Do deep learning models really outperform traditional approaches in molecular docking? arXiv preprint arXiv:2302.07134 (2023).