大模型之间的战争,人类精英杀红了眼。
谷歌不再顾忌AI发展带来的风险,解开了身上缚龙索。
面临生存危机时,不作恶就暂时放一边。
虽然AI大爆炸人类后果难测,但洪水滔天再说。
管它呢,一起毁灭吧!
2023.05.11,谷歌PaLM2直接对抗GPT-4,摒弃伦理放飞自我。
AI军备竞赛,已然不可停止。
冥冥之中,人类命运在此分野?
还记得三月底,人类提出要“封印AI”六个月。
但小石入海,掀不起任何波澜。
原因很简单,人类已经堕入“囚徒困境”。
就算AI教父Hinton出走,并称人类可能被取代,但谷歌不为所动,力推最强模型PaLM2。“猜疑链”一旦形成,那管什么“人类命运”。
此时的人类精英和科技巨头,像极了博弈论困境中的囚徒,想尽办法保护自己,但最终导向可能是一个最悲剧的结果:
以上只是人类在AI大爆炸中面临的一种困难,“诸神之战”最后是人类崛起。那“百模大战”的结局呢?是不是人类之黄昏?
人类此次发起的AI战争,后果难以预测。
而战争又集中到大模型,人类再无退路。
不仅仅是“囚徒困境 ”,以下12条定律,映照着人类自身的无奈。
一旦一只领头羊做出某个行为,羊群就会跟随和模仿,甚至担心自己没有抓住时机。
这就是典型的“羊群效应”,在科技发展领域体现得更加淋漓尽致。
一旦某项新技术或新产品成功,就会有大量企业纷纷跟进。
P(X) = α * P(X_m) + (1 - α) * P(X_i)
P(X) 表示个体选择选项 X 的概率,α 是羊群效应的权重参数,P(X_m) 是大多数人选择选项 X 的概率,P(X_i) 是个体独立选择选项 X 的概率。
个体的决策概率受到大多数人决策概率的影响,当 α 接近 1 时,个体更倾向于跟随大多数人的决策;当 α 接近 0 时,个体更倾向于独立决策。
ChatGPT横空出世,很多企业都加入了大模型之争中。
有老牌传统科技巨头,有新兴的互联网公司,还有很多名不见经传的企业……
仅仅是国内,根据统计发现,目前已有30多款大模型出现。
而实际上正在研发的,可能远远不止这个数量。
幸存者偏差:
被淘汰者不说话
幸存者偏差,又称生存者偏差,是一种常见的逻辑谬误。
就像是“没来的同学请举手”一样,是统计学魔鬼在玩魔术。
它只考虑幸存下来的样本,而忽略了那些已经消失的样本。
了解幸存者偏差,可以定义以下变量:
P(x):表示个体 x 存在于总体中的概率。
S(x):表示个体 x 存在于筛选过程中幸存的概率。
F(x):表示个体 x 未幸存的概率。
根据幸存者偏差的观点,幸存的个体更有可能被观察到,而未幸存的个体则更容易被忽略,可以使用以下数学建模来表示幸存者偏差:
P(x | S) = P(x) * S(x) / ∑[P(y) * S(y)]
(对所有 y)
其中,P(x | S) 表示在幸存条件下个体 x 的存在概率,∑[P(y) * S(y)] 表示所有幸存个体的总和。
在大模型之争中,人们只看到了ChatGPT这样的成功者。
但往往不知道,有很多企业已经被市场淘汰出局。
它们可能因为技术力不足和资金短缺等种种原因,早早倒在这片沙场上。
在任何一个系统中,最重要的只占约20%,其余80%都是次要的。
假设有一个集合,其中包含N个元素。设集合中有N个元素,记为X={x1, x2, ..., xn}。假设X的重要性、价值或影响力分别用I(x)表示。
将X按照I(x)从高到低进行排序,得到排序后的集合Y={y1, y2, ..., yn},其中y1表示最重要的元素,yn表示最不重要的元素。
根据二八定律,选择Y中的前20%的元素,记为Y_20={y1, y2, ..., y0.2N},它们占据了整体重要性、价值或影响力的80%。
剩下的80%的元素,记为Y_80={y0.2N+1, y0.2N+2, ..., yn},它们只占据了整体重要性、价值或影响力的20%。
在大模型之争中也是如此,大模型需要庞大的算力、数据和算法训练作为支撑。
能够满足这一需求的,只有少数几家科技巨头。
换句话说,大模型的训练就是一个“烧钱”项目。
所有与AIGC相关的产业和公司,每一个后面都站着一个巨头,甚至自己就是巨头本头。
而正是因为这个原因,最终掌握大模型话语权的也是这些科技巨头。
它们将成为最重要的那20%,在未来的AIGC时代呼风唤雨。
一些人或组织在共同努力下取得的收益,被一些其他人或组织不努力也能分享收益。
搭便车是人类本性,经常有人嘲讽国内的科技企业:人家一开源我们就创新 。平时不在科技创新上坐冷板登,等着别人开源然后搭便车。
搭便车博弈可以假设有 N 个参与者,标记为 1, 2, 3, ..., N。每个参与者都有两种选择:付出努力(E)或搭便车(F)。
参与者i的效用函数表示为Ui(E, F),表示参与者i根据自己的选择和其他参与者的选择获得的效用。假设效用函数满足一定的性质,如单调递增性和有界性等。
搭便车博弈可以用一个N × 2的行动矩阵表示,记作A=[a_ij],矩阵中的元素可以通过参与者之间的互动关系和效用函数来确定。
美国《财富》曾在三月份报道称,美国近50%的企业已经开始用ChatGPT。
有48%的已经让其代替员工工作。还有89%的大学生在用ChatGPT做作业。
随着时间推移,这个比例只会越来越高。
虽然在大模型发展中,中小企业和个人很难承担大量的时间和资源投入。
但他们却可以从大企业的研究成果中受益,利用已训练好的大模型解决自己的问题。
囚徒困境:
谁都害怕对方更强
马斯克等人曾发起联名信,呼吁停止发展大模型。
但这是绝对不可能的事情,因为人类已经堕入了“囚徒困境”。
囚徒困境是博弈论中非零和博弈的代表性例子。
其中最有名的例子是“两个嫌疑犯作案后被警察抓获,最后都选择了揭发对方”。
囚徒反映的是个人最佳选择,而非团体最佳选择。
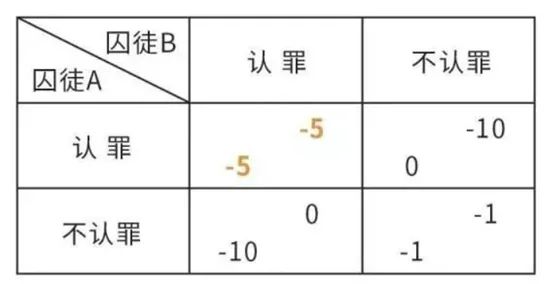
在囚徒困境下,所有人都担心其他人会制造出更强大的大模型。
这样就会被迫进入AI军备竞赛,没有人会停止,反而会加大力度研究。
一旦你停止了研究,很可能就会被人反超而失去竞争力。
最后的结果可能是人类自相坑害队友,而AI成为那个收获人类成果的警察,将人类关入牢笼之中。
创造性破坏理论:
为了生存必须变革
约瑟夫·熊彼特在20世纪初提出“创造性破坏理论”。
新兴企业通过创新和技术进步,取代和淘汰原有的企业和产业,促进经济发展和进步。
在人工智能领域,ChatGPT的出现无疑打破了过往的产业规则。
它与十多年前Iphone一样,具有划时代的意义。
这也代表着传统的自然语言处理方法将被彻底替代。
对于企业来说,如果无法及时适应新技术和市场变化,就可能被取代。
要适应不断变化的市场和技术环境,就必须保持持续的创新和变革。
这也是国内外众多传统科技企业如履薄冰的原因,毕竟诺基亚塞班的命运还历历在目。
凡有的,还要加给他叫他多余;没有的,连他所有的也要夺过来。
这就是马太效应,在一项活动或领域中,成功的个体或组织总能得到更多的机会和资源,从而比起其他人更容易取得成功的现象。
其中,Y表示某一指标(如资源、财富、权力)的累积量,X表示个体或单位的某一属性(如初始资源、能力、影响力)的量,k是一个常数,n是大于1的指数。
个体或单位的初始属性越大,其累积量的增长速度就越快。这意味着在一个具有马太效应的系统中,资源或权力倾向于向少数拥有更多初始属性的个体或单位聚集,导致差距的进一步扩大。
在大模型的竞争中,谷歌和微软等大企业由于其巨大的资源和先进的技术,使得在研究和发展中拥有更多的机会和优势,从而进一步巩固其在这个领域的地位。
而中小企业资源有限,很难挑战和跨越这些大山。
强者愈强,AIGC最后的结局,很大可能还是落到垄断寡头手中。
摩斯科定律:
第一个不一定最好
美国管理学家R·摩斯科曾提出:
所以要不断追问,打破砂锅问到底。
而在大模型的竞争中,摩斯科定律有另外一种解读。
越先出现的人工智能大模型,不一定是最好的大模型。
大模型的发展需要不断地迭代和改进,新的算法、技术和方法会不断涌现。
更早出现的大模型,可能会有更多技术积累。但这并不代表后来者没有任何机会。
这也是为什么这么大公司不放弃的原因,摩斯科定律给了信心。
人们在技术发展方面,往往会高估其短期的效益,却低估长期的影响。
阿玛拉定律将短期效益表示为 B_s,长期影响表示为 B_l。可以使用下面的数学公式来表示这种关系:
这个不等式表示了短期效益大于长期影响,即人们倾向于更关注和重视短期利益,而对长期影响的重要性进行低估。
大模型研究也是如此,目前我们可能高估了它的短期收益。
所以当资本纷纷进入这一行业时,不免会产生泡沫。
但从长远来看,AI可能真的带来的是一种革命,至于革谁的命,就很难说了。
手表定律:
越多可能越混乱
手表定律是指一个人有一块表时,可以知道当时是几点钟,当他同时拥有两只表时,却因为两只表的微小不协调,丧失对两只表的时间刻度的信心。
我们可以用以下方式表示手表定理:
N:行为或决策选项的数量。
t(N):选择某个选项所花费的时间,t(N)是一个关于N的函数。
T(N):总共花费的时间,T(N) 是t(N)的累积和。
随着选项数量的增加,总体花费的时间呈二次增长(即平方级增长)。即:
其中,a 是一个正比例常数。随着选项数量N的增加,总体花费的时间T(N)增长得更快。
按照目前情况来看,未来大模型会越来越多。
每个人能够选择的大模型会很多,但可能会变得更加混乱。
举个例子,如果询问同一个问题,得到的却是不同的答案。
那么人们该相信哪个答案?
最终这个问题会不会影响到人类的整体行为?
这可能是每一个研发大模型的企业都该思考的问题。
一个系统中,在初始条件下哪怕微小的变化都能带动整个系统巨大的连锁反应,这是一种混沌现象。
形象化来比喻就是:一只南美洲亚马逊河热带雨林的蝴蝶,偶尔扇动几下翅膀,两周后可能引起美国德克萨斯州的一场龙卷风。
蝴蝶效应可以表示一个动力系统中的天气模型。以下是洛伦兹系统的数学表达式:
在上述方程中,x、y和z是状态变量,σ、ρ和β是常数参数,t是时间。
它表达了空气流体运动的复杂性,微小的变化可能会在系统中产生非线性和长期的影响,导致系统走向完全不同的轨迹。
同样的,我们永远都不知道,正在训练中的大模型,是不是那扇动翅膀的蝴蝶。
某个算法或技术的微小变化可能会在整个系统中引发重大的变化。
这个微小变化,又会不会对未来整个人类社会产生某种影响。
冰山理论:
更多的我们看不到
就好比冰山,露出水面的只是它的百分之一,水下的部分却足以击沉无数次泰坦尼克号。
其中,S 代表事物的总体大小,V 表示可见的部分,H 表示隐藏的部分。这个方程表达了冰山的结构,我们只能看到冰山露出水面的部分,而水下的冰块则是隐藏的。
所以,无论是ChatGPT,还是PaLM2。
我们看到的只是它强大工具性的一面。
很多底层技术、算法等是我们不了解的。
而这些,才是至关重要的一部分。
2023年,是人类将自身推向悬崖的一年吗?
ChatGPT vs PaLM2,不过是大模型战争的一个缩影。
成百上千个大模型在酝酿,时刻会破土而出。
人类正陷入一场混乱而失控的军备竞赛。
更恐怖的是,对更强大的AI,没有人能够理解、预测和控制。
所以,人类精英们越是努力,碳基生命就越是危险。
面对AI黑盒,人类能100%保证它不会反向颠覆吗?
没有规则限制,没有法律制约,谁都不知道下一步会发生什么。
有人说,担心这个是庸人自扰、杞人忧天。
但要承认,有些错误人类一次都不能犯。
你敢想象《黑客帝国》的故事真正发生吗?
如今的人类,踏上了一辆没有刹车按钮的列车。
什么时候会因为变换轨道而掉落悬崖呢?
真到了那个时候,人类怎么办?
现实世界,谁来拯救人类?
ChatGPT COURSE
量子学派×喜马拉雅
联合推出
「ChatGPT第一课:
武装我们第2大脑」
量子学派-重磅打造
ChatGPT系统化大众课程
喜马拉雅-边听边学
碎片化时间掌握AIGC前沿知识
1、读懂技术原理
2、理解产品本质
3、掌握底层逻辑
4、思考AGI未来
从零开始
玩转ChatGPT
武装第二大脑
走进碳硅协作进行时
点击下方链接购买或扫描二维码咨询
▼ 咨 询 课 程 ▼