在结晶固体中,外部热或机械刺激引起的结构不稳定性几乎完全发生在定义明确的结构缺陷处,例如位错。然而,无序固体缺乏长程平移对称性。因此,很难识别某种结构缺陷。在过去的几十年里,已经出现了一些现象学模型来理解无序固体中塑性重排的结构起源。这些模型的共识是,无序固体中的原子重排可能源于一些松散堆积的区域,这些区域充当结构“缺陷”。最近,研究人员通过采用新兴的监督机器学习 (ML) 方法确定了与重排相关的结构“缺陷”。尽管通过监督机器学习 (ML) 模型的开发在预测各种无序系统的局部结构不稳定性方面取得了重大进展,但这些模型的泛化和可解释性仍有待解决。
基于系统分析,来自北京计算科学研究中心和杭州电子科技大学的学者发现ML预测模型的权重函数与预测系统的径向分布函数(RDF)之间存在显着相关性。本研究进一步提出了一个密度涨落模型,其中每个原子的径向对称函数作为局部结构描述符,修改后的全局 RDF 作为权重函数。与最近需要利用动态信息作为监测信号的 ML 预测模型不同,该模型仅基于静态结构信息,具有良好的泛化能力。与其他广泛研究的结构参数相比,该模型可以为不同的 MG 系统提供更可靠的结构不稳定性预测能力。本研究的发现揭示了局部结构不稳定性的密度波动特征,并阐明了无序材料中的结构-性能关系。相关文章以“Machine-learning inspired
density-fluctuation model of local structural instability in
metallic glasses”标题发表在Acta
Materialia。

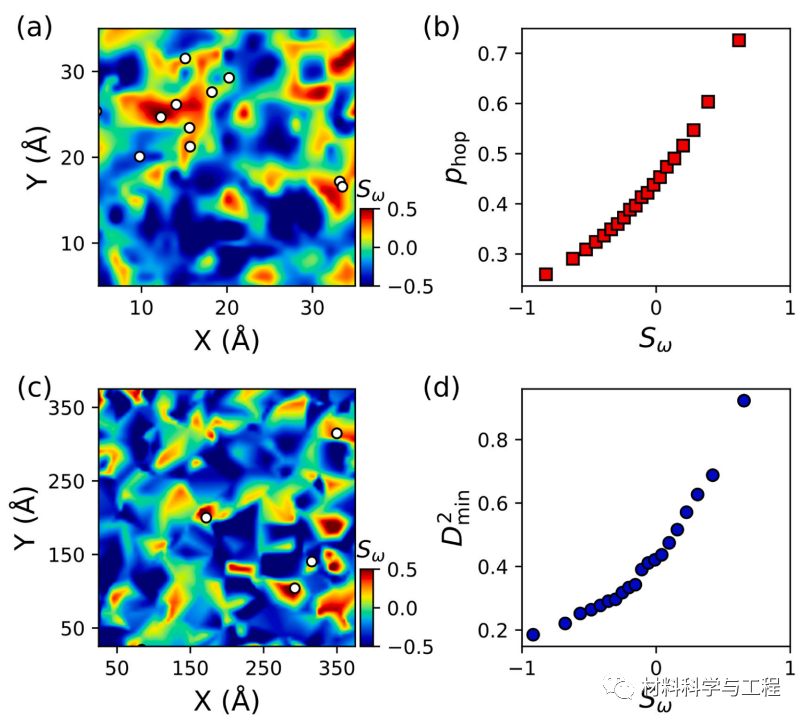
图 1. 使用柔软度 (Sω) 预测塑性重排。 (a)-(c) 等高线图分别表示Cu50Zr50 SL 的 10
Å 厚切片和 Cu50Zr50 MG 的 0.1 Å 厚切片中的柔软度 (Sω)。(b)-(d) 平均 phop 和 D2min 分别与 Sω的相关性。
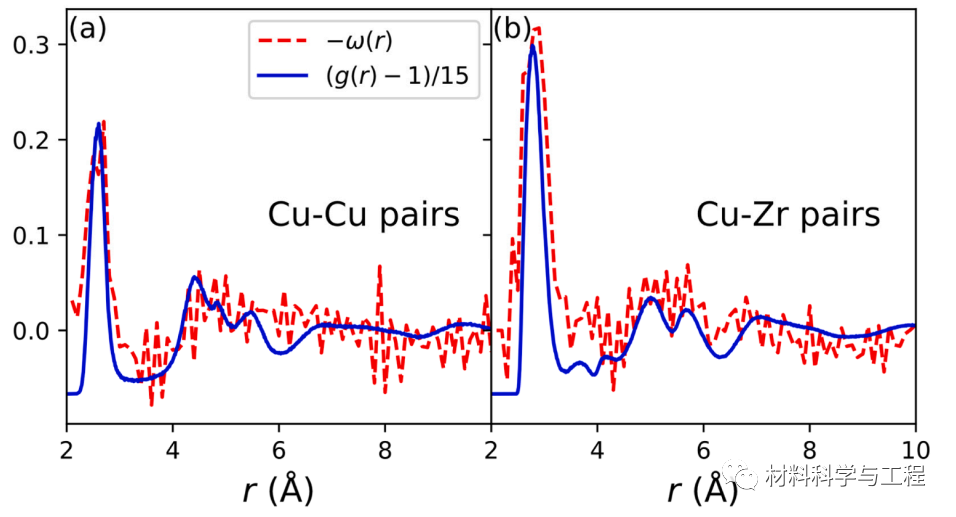
图 2. Cu50Zr50MG的超平面法线与修正径向分布函数的相关性。 (a)-(b)对于Cu-Cu和Cu-Zr对,超平面正态−ω(r)以及修饰径向分布函数[g(r)− 1]/15分别作为距离r的函数
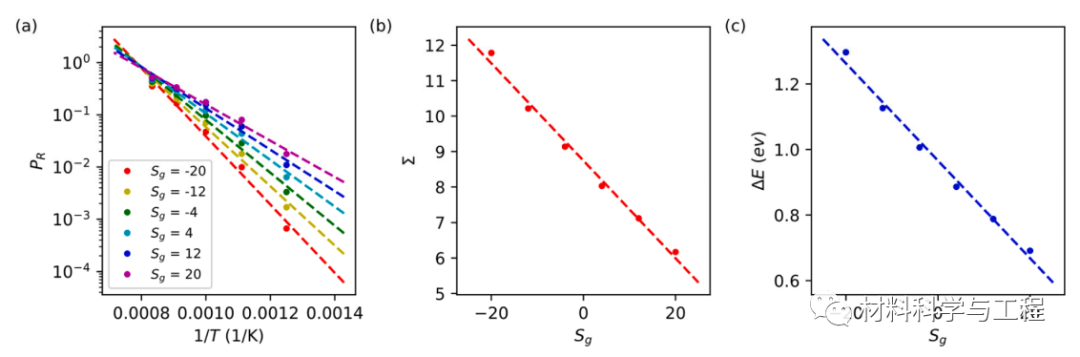
图 3 径向柔和度与动态的关系。(a) 重排概率,PR(Sg),作为 1/T 的函数,对于 Cu50Zr50SL 的六个不同的软度值,从 Sg = −20 到 Sg = 20。 (b)熵标度 Σ 与 Sg。 (c) 能量标度,ΔE,与 Sg的关系
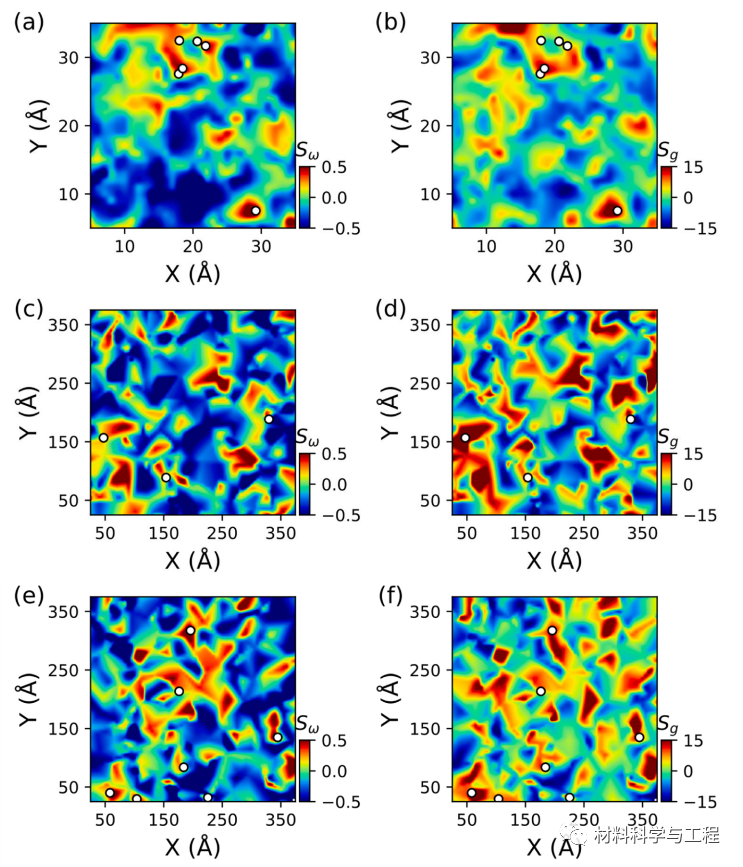
图 4. 柔软度 (Sω) 和径向柔软度 (Sg) 的比较。 (a)-(b) 等高线图分别表示 Cu50Zr50SL 的 10 Å 厚切片中的 Sω 和Sg 场。 (c)-(d) 等高线图分别表示 T = 0 K 时 Cu50Zr50 MG的 0.1 Å 厚切片中的 Sω 和Sg 场。 (e)-(f) 等高线图分别表示 T = 300 K 时 Cu50Zr50MG 的 0.1 Å 厚切片中的 Sω 和Sg 场。
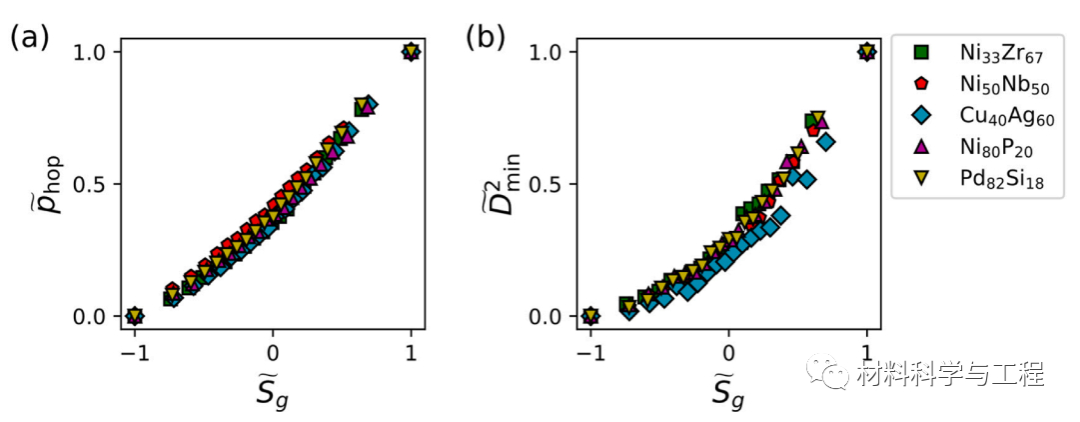
图 5. Sg与动力学之间的相关性。 (a)-(b) Ni33Zr67、Ni50Nb50、Cu40Ag60、Ni80P20 和 Pd82Si18系统的归一化 phop 和 D2min 与归一化 Sg 之间的相关性。
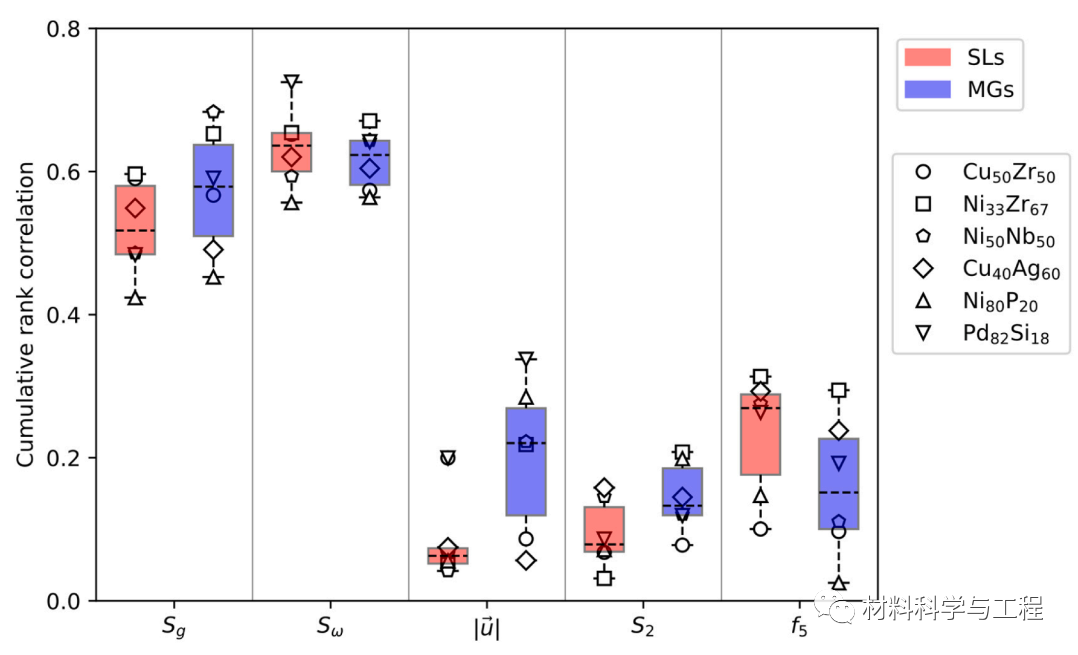
图6.单个结构指标与动态之间的累积排名相关性比较。显示了Cu50Zr50,Ni33Zr67,Ni50Nb50,Cu40Ag60,Ni80P20和Pd82Si18SL和MG的结果。在箱形图中,箱形的边界跨度为 25% 到 75% 百分位数,虚线表示中位数。
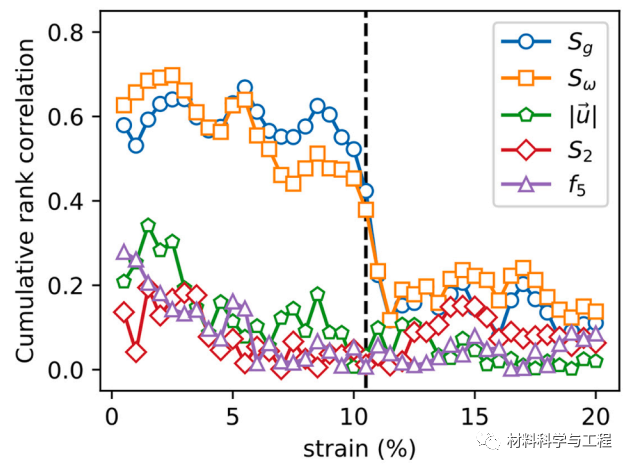
图 7. 计算单个结构指示剂长块与 D2 min 之间的累积秩相关性,作为 Cu50Zr50MG 应变的函数。
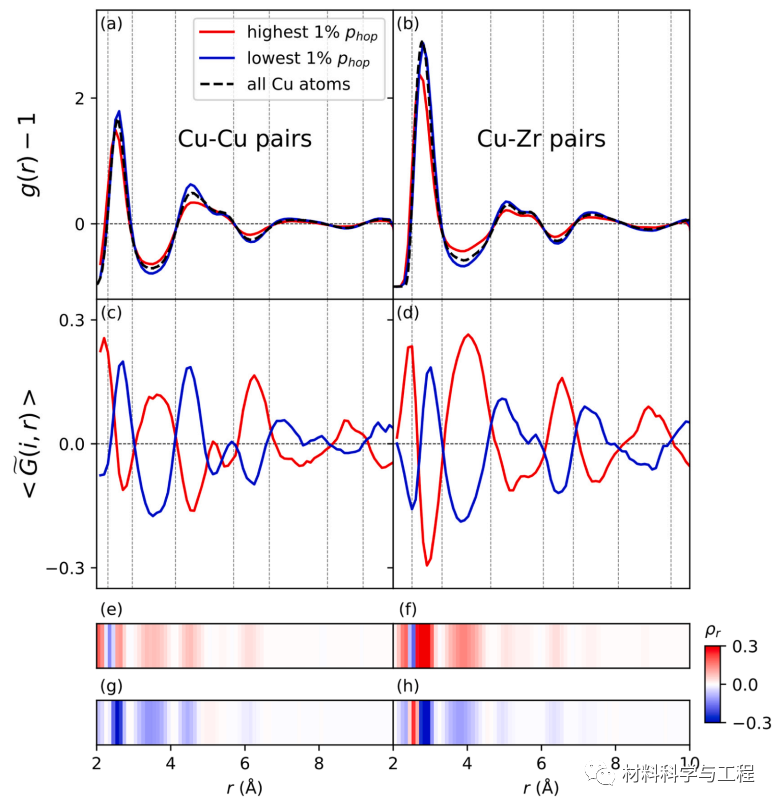
图 8. CuZr SL 重排原子和非重排原子之间的结构差异。 (a)-(b) gCuCu(r) - 1 和 gCuZr(r)
- 1 分别作为距离 r 的函数。 (c)-(d) 平均结构特征CuCu (i; r)> 和 `CuZr(i;
r)> 的分布。 (e)(f) 结构编码特征的分布,ρCuCur = − [gCuCu(r)− 1]〈 G`CuCu(i; r)〉 和 ρCuZrr = − [gCuZr(r) − 1] 〈 G`CuZr(i ; r)> 分别用于快速 Cu 原子。 (g)-(h) 慢速 Cu 原子的结构编码特征分布,分别为 ρCuCu r 和 ρCuZrr
总之,本研究提出了一种新的密度波动模型,用于识别静态过冷金属液体和剪切 MG 中的结构不稳定性。原子 Sg 是通过使用径向对称函数作为原子结构表示结合系统的修改 RDF 作为权重函数来定义的。因此,与之前的监督 ML 方法相比,它是一个纯粹的结构指标,仅依赖于静态结构。此外,密度波动模型是针对不同化学系统的可解释和可推广的模型。此外,与仅基于静态结构的其他广泛使用的结构参数相比,Sg 可以更好地预测热或应力诱导的重排。本研究提出的 Sg概念为阐明无序材料中的结构-性质关系开辟了新的机会。(文:SSC)
本文来自微信公众号“材料科学与工程”。欢迎转载请联系,未经许可谢绝转载至其他网站。
