
论文信息:
Qiyan Ren, Yan Zhou, Lechuan Hu, Chengchao Wang, Jian Liu, Lanxin Ma,Linhua Liu.Evaluation and design of photothermal conversion performance for multiple“complex-morphology” nanofluids via bidirectional deep neural network, Applied Thermal Engineering, 2023.
论文链接:
https://doi.org/10.1016/j.applthermaleng.2023.121954
纳米流体具有良好的光学和热性能,已被广泛应用于太阳能收集的潜在工作流体和太阳能蒸汽产业。本文采用了机器学习与高通量辐射传输计算相结合的方法,对各种纳米流体的整个光热转换过程进行了全面的分析。通过调节纳米粒子的形状、材料成分和几何参数,可以实现共振吸收峰和光谱吸收的调制。同时还建立了一个包含14060组纳米流体的设计空间数据集。基于该数据集证明了双向深度神经网络模型是正向和逆问题的有效可靠的解决方案。本工作为评价纳米流体在光热转换中的性能提供了一个总体框架,也是一种准确、有效地预测和设计纳米流体的方法,具有广泛的适用性。
纳米流体的辐射转移过程如图1(a).所示,本文研究了五种具有等离子体共振性质的粒子见图1(b)。采用等体积有效半径均匀地描述粒径。对于核壳纳米球,它由半径为rc的核粒子和厚度为ts的壳粒子组成,CSR=/rc为核壳比。对于纳米棒,长径比AR用直径D和长度L来描述。对于纳米棒,a是立方体的边长。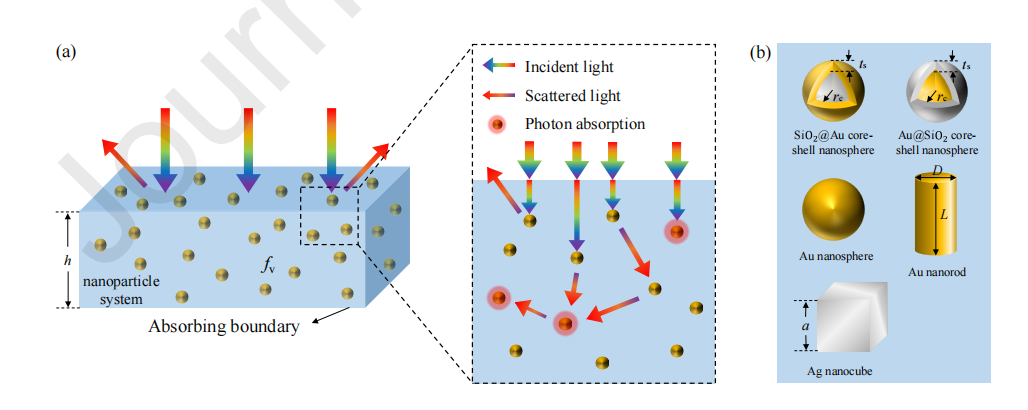
图1.示意图 (a)光通过纳米流体进行传播的过程 (b)NPs的类型和几何参数。 本文设计的双向深度神经网络结构
见图2,由一个预先训练好的前向神经网络和一个全连接的反向神经网络组成。为了训练模型,首先训练正向神经网络,利用材料和几何参数高精度地预测纳米流体的吸收光谱Aλ。神经网络的训练和构建决定了隐藏层中的层和神经元的数量。通过最小化损失函数来最小化预测值和真实值之间的均方误差(MSE)的训练过程 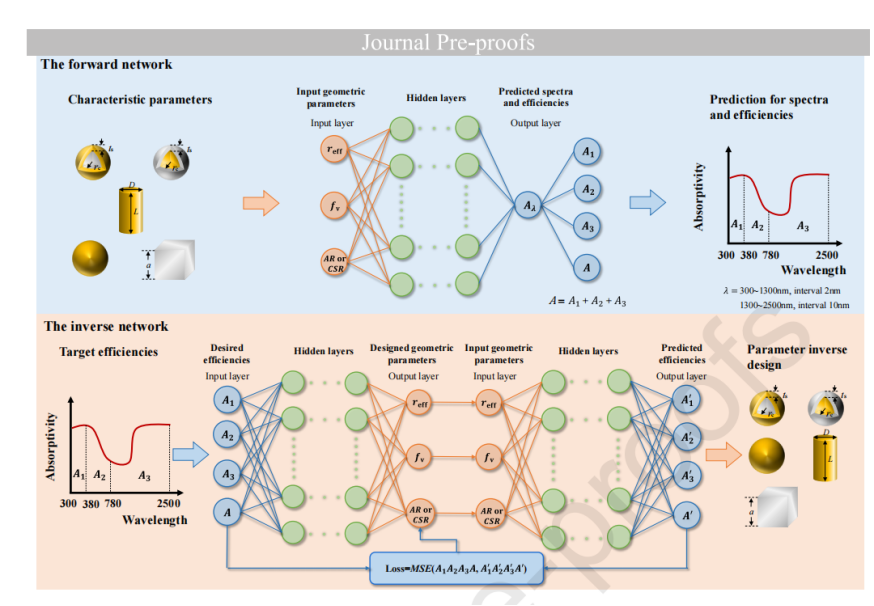
图2.用于预测吸收光谱和太阳吸收效率,以及设计纳米流体几何参数的双向神经网络结构示意图。
用t矩阵和DDA法计算的吸收效率系数与Lorenz-Mie结果的比较如图3(a).所示,除了验证了单个粒子的吸收效率因子外,还比较了用蒙特卡罗方法对辐射传输的理论计算。图3(b)比较了Chen等人研究得到的光谱吸收率与本文提出的蒙特卡罗方法计算的结果。结果显示偏差小于3%,验证了该方法的准确性。 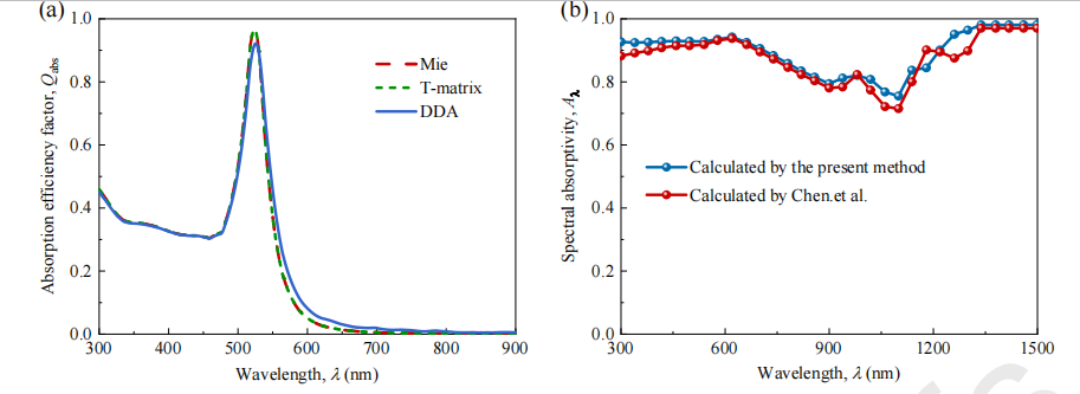
图3. (a)通过洛伦兹-米理论、t矩阵和DDA的方法计算得到Au NS的吸收效率因子;
(b)Chen等的结果与本文的方法对Cu@C纳米球悬浮液的光谱吸收率的比较。图4为不同类型和尺寸的NPs的吸收效率系数与波长的变化函数。图4表明,在300~2500nm的波长范围内,有效半径对所有NPs的吸收效率因子都有明显的影响。从图5(a)-(c)可以看出,随着粒径的变化,存在一个最大的吸收峰。此外,共振吸收峰位置的变化对球形粒子的反射不敏感。从图4(d)-(f)可知吸收峰的最大值随有效半径值有显著变化。总体说来,粒径是确定NPs的吸收效率因子和吸收峰的关键。(a)Au NS, (b) SiO2@Au NS, (c) Au@SiO2 NS, (d)-(e) Au NR, and (f) Ag NC。 核壳比对核壳纳米粒子的光学性能的影响如图5所示。比较图5(a)、(b),可以看出两种粒子共振吸收峰与核壳比值的变化有显著差异。对于SiO2@Au NSs,共振吸收峰的最大值和位置均随CSR的变化而变化,而对于Au@SiO2 NSs,只有前者发生变化。对于旋转对称纳米棒,长宽比是影响光学性能的另一个重要因素。图5(c)、(d)显示了长宽比对于旋转对称的纳米棒光学性能的影响。如图5(c)所示,当AR < 1时,可见光谱和近红外光谱之间出现了两个共振吸收峰。在近红外范围内,共振吸收峰的最大值和位置都随着AR的增加而变化,而只有前者在可见光范围内发生变化。从图5(d)可以看出,当AR增大时,共振吸收峰位置随着AR的红移,当AR > 1时,其最大值也增大。与reff相比,共振吸收峰的变化对AR更为敏感。图5.不同CSR或AR条件下的吸收效率因子随波长的变化(a) SiO2@Au NS, (b) Au@SiO2 NS, and (c)-(d) Au NR。 图6(a)-(c)可知,随着体积分数fv的增加,Au NS纳米流体的光谱吸收率Aλ逐渐增加,并且半径越小越敏感。图6(d)-(f)显示了具有不同几何参数和体积分数fv的SiO2@Au NS纳米流体的吸收光谱。当半径从10nm增加到50 nm时,在fv = 1×10-4时对纳米流体光谱吸收率有轻微的影响。随着fv从1×10-5增加到1×10-4,Aλ有明显的变化,较小的CSR(CSR = 0.1)表现出更好的全光谱吸收特性。因此有必要共同调整多个参数来提高SiO2@Au NS纳米流体的光谱吸收率。不同reff、fv和AR的Au NR纳米流体的吸收光谱见图6(g)-(i),可以看出,随着reff从10nm增加到90nm,Aλ值显著降低,而与reff相比,Aλ值对fv和AR的变化敏感性较低。以上结果表明,纳米流体的吸收光谱受到多种因素的影响且光学/辐射特性与单个粒子有显著差异。 图6.(a)-(c) Au NS nanofluids, (d)-(f) SiO2@Au NS nanofluids, and (g)-(i) Au NR不同reff、fv和AR(或CSR)条件下的吸收光谱。
由图7(a)和(b)可以看出,在500~600nm波长内,太阳吸收随着r的增加而降低,而在600~1000nm范围内,r=为10 nm的纳米流体则明显减小。图7(b)显示在300~900nm波长内,与纯水相比,Au NS纳米流体对太阳能的吸收和利用大大提高,且对太阳能的吸收随fv的增加而增加。图7(c)反映出用高fv降低纳米流体的半径是获得更高的太阳吸收效率的有效途径。 图7. h=为10 mm的Au NS纳米流体在不同(a) r 和
(b) fv下的光谱辐照度;(c)r和fv对Au NS纳米流体太阳吸收效率的变化。从图8(a)可以看出,在可见波长范围内,纳米流体在可见波长范围内的太阳吸收有所提高,而在750~1100nm波长内,半径小则太阳吸收显著降低。从图8(b)可以看出,当fv =1×10-5,在750~1100nm波长之间时,增加fv可以显著提高纳米流体对太阳的吸收。图8(c)显示出CSR的减少导致了对纳米流体的太阳吸收的显著增加。太阳吸收效率随着rc或CSR的降低而增加,这为具有较高fv的SiO2@Au NS纳米流体提供了更灵活的效率调整。 图8.h=为10 mm的SiO2@Au NS纳米流体在不同 (a) reff、(b) fv和 (c) CSR中的光谱辐照度。为了研究几何参数和体积分数在调节光热转换性能中的作用,计算了金纳米纳米流体的光谱辐照度和太阳吸收效率。具有reff、fv和AR的金纳米纳米流体的光谱辐照度变化如图9(a-c)所示。从图9(a)可以看出,反射为10 nm的纳米流体在500~950nm波长内具有更好的太阳吸收能力,并具有更好的太阳吸收特性。然而,reff 为50 nm的纳米流体在950~1300nm之间具有更好的太阳吸收。与图9(b)中的纯水相比,纳米流体的加入显著提高了对太阳能的吸收。如图9(c)所示,AR的增加对Au NR纳米流体的太阳吸收影响较小。在图9(d-f)中,分析了在fv为1×10-5~1×10-3时,reff和AR对纳米流体太阳吸收效率的影响。图9(d)和(e)表明,当fv增加时,降低reff或AR有利于Au NR纳米流体的太阳能吸收效率。
随着reff的降低,在fv =为1×10-3时,太阳吸收效率显著提高,但对AR的敏感性降低,如图9(f)所示。图9.h=为10 mm的Au NR纳米流体在不同(a) reff、(b) fv和(c) AR中的光谱辐照度;在(d)ff=1×10-5,(e)fv=1×10-4,(f)fv=1×10-3下Au NR纳米流体太阳吸收效率的变化。
本文训练了一个双向神经网络,根据几何参数准确预测吸收光谱和太阳吸收效率。然后,根据期望的效率进行几何参数的逆设计。由于数据量大,仅部分数据集如图10所示,可以表示数据集的数据分布。由图可知球形纳米粒子的太阳吸收效率比非球形纳米粒子的太阳吸收效率覆盖范围更广。由图10(a)知,与Au NS纳米流体相比,具有表面等离子体共振的SiO2@Au NS纳米流体在相同的粒径下具有更高的光热转换效率。由于纳米粒子光学性质的变化,非球形纳米流体的太阳吸收效率随着有效半径的增大而明显降低,如图10(b)所示。
图10.五种类型的纳米流体的太阳能吸收效率数据集的5%神经网络利用训练数据在训练过程中不断地改变连接权值。随着连续训练,损失函数逐渐减小,直到达到收敛。选择Au@SiO2 NS纳米流体进行分析损失函数。图11(a)显示,随着周期的增加,训练集和验证集都呈现出一个减小的损失函数。MSE在真实值与预测值之间的统计分布如图11(b)所示,其中正向预测的精度超过99%,证实了其进行吸收光谱预测能力的可行性。从测试集中随机选择的每种类型的纳米流体的吸收光谱的预测结果如图12(a)-(e)所示。此外,在图12(f)中比较了五种类型的纳米流体的预测的太阳吸收效率和真实的太阳吸收效率。结果表明,正向神经网络的训练几乎可以完美地预测任何类型的纳米流体的光谱。 图11.(a)Au@SiO2 NS纳米流体的训练和验证集的损失函数;
(b)真实与预测之间所有类型粒子的MSE数据分布。图12. (a) Au NS纳米流体、(b) SiO2@Au NS纳米流体、(c) Au@SiO2 NS纳米流体、(d) Au NR纳米流体和(e) Ag NC纳米流体的吸收光谱模型预测和数值模拟结果的比较。为了解决“一对多”的问题,利用双向神经网络结构实现了纳米流体的设计,本文以目标太阳吸收效率作为输入,以设计的参数(reff、CSR或AR、fv)作为输出,也记为中间层。预先训练好的前向神经网络(由7个隐藏层组成,包含1200个神经元)直接接收输出参数来预测效率。逆神经网络通过最小化损失函数来进行优化,损失函数是输出预测效率和输入效率之间的MSE。期望与设计的MSE之间的数据分布统计数据如图13(b).所示,纳米流体的大部分值均小于0.1。这表明逆设计的精度超过93%,说明本文的模型在准确确定所需效率的结构参数方面得到了很好的支持。图13.(a)Au@SiO2 NS纳米流体的训练和验证集的损失函数;
(b) 目标粒子和设计粒子之间所有类型粒子的MSE数据分布。此外,作者进行了一个随机选择过程来评估逆神经网络。为了获得所需的NPs几何参数,逆神经网络结合了目标效率值。通过仿真计算将设计的结构转换为有效的设计,观察到设计结果与之前的目标结果之间有很强的一致性。即使在目标参数和设计参数之间存在显著差异,它们仍然表现出相似的效率。如图14所示,其中对应的光谱也表现出高度的相似性。图14(a)-(e)比较了目标光谱(实线)和设计光谱(彩色线),图14(f)显示了期望效率和设计效率之间的差异。如图所示,设计的效率和目标效率之间的区别可以忽略不计,这进一步证明了该逆神经网络是可靠的和准确的。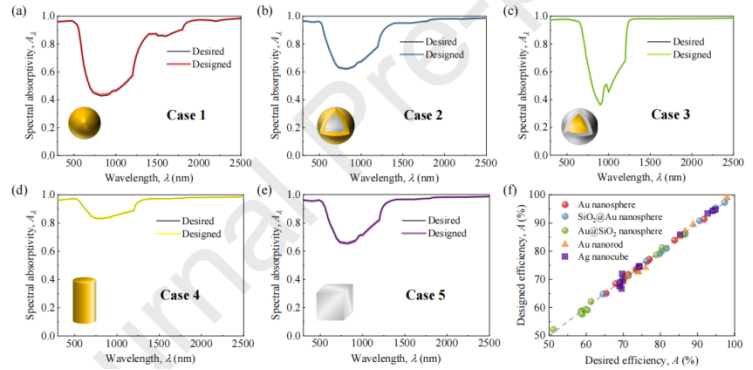
图14. (a) Au NS纳米流体、(b) SiO2@Au NS纳米流体、(c) Au@SiO2 NS纳米流体、(d) Au NR纳米流体和(e) Ag数控纳米流体的逆设计解决方案
本文提出了一个双向深度神经网络模型,有效地解决了利用纳米流体转换太阳能的正向和逆设计问题。结果表明,不同纳米流体的光谱吸收率受其对几何参数的灵敏度的影响。此外,SiO2@Au NS纳米流体在CSR 为0.1时表现出增强的全光谱吸收特性。双向深度神经网络的利用提供了一种系统的方法来准确评估纳米流体的光热转换效率,准确率为99%。考虑对生成的设计进行实验验证,通过考虑在实际应用中影响决策的因素,如经济效益,来进一步完善整体框架。
招聘信息 | 山东高等技术研究院吴小虎课题组招收联
合培养研究生、科研助理和博士后
点击下图查看详细招聘信息
!
