声明:该论文为研究团队成员阅读到的优秀文献,非本推文作者原创。
原文出处:Liu X, Chen X, Tian M, et al. Effects of buffer size on associations between the built environment and metro ridership: A machine learning-based sensitive analysis[J]. Journal of Transport Geography, 2023, 113: 103730.
利用更细粒度的大数据和非参数机器学习方法,该研究对300m、600m、800m和1000m四种径向缓冲区范围内的建成环境要素与地铁客流的关系进行了敏感性分析。研究结果有助于规划人员为站点地区规划和需求预测制定地铁汇水区基准,更重要的是,研究结果强调了精心选择基于面积的变量的分析空间单元的重要性,特别是在使用非参数机器学习方法进行研究时。
1.研究区域与变量
本研究以上海为个案进行研究。该研究使用了上海地铁的数据,特别是2019年9月18日(一个典型的星期三)记录的乘客人数数据。该数据集包括了上海17条线路上341个站点的每日客流量数据,如图1所示。
DRM共包括15个自变量,并将其分为两组:(1)建成环境变量和(2)站点特征变量。表1提供了本研究所使用的所有自变量和因变量的详细描述。
2.分析方法
2.1机器学习方法:eXtreme Gradient Boosting
由Chen和Guestrin提出的XGBoost在城市和交通研究中越来越受欢迎。它是一种稳健的机器学习算法,以能够处理大型数据集和建模复杂、非线性关系而闻名。它的设计允许对大数据和错综复杂的模式进行高效处理,在预测精度上超越了传统的线性模型。
在数学上,XGBoost使用加性函数来预测最终结果,如式(2)所示:
至于确定每棵树的结构,需要最小化的学习目标如下:
其中,后面的Ω(fk)表示正则化参数,如公式(4)所示:
对于固定的结构q(x),我们可以通过公式(5)计算出叶j的最优解ωj*,并通过公式(6)简化目标函数。
2.2解读机器学习:SHapley Addictive explanations
为了解释该研究中的XGBoost模型,研究者使用了由Lundberg和Lee提出的一种复杂的机器学习解释方法——夏普利加法(SHAP)技术。SHAP通过利用Shapley值的可加性属性将全局解释与局部解释合并。
SHAP是一种一致的特征归因方法,使用线性公式结合变量效应之和和截距作为预测的近似值,如公式(7):
特征归属由Shapley值φi表示,定义为所有可能差异的加权平均值:
为了获得最优的参数设置并避免过拟合问题,使用五折交叉验证程序来训练XGBoost模型。经过迭代,当树的数量、深度和收缩率设置为表2中的参数时,性能最佳,平均绝对误差(MAE)、均方根误差(RMSE)和R2最低。
1.XGBoost模型的性能
该研究在4个不同的缓冲区(见表3)内比较了传统OLS模型和XGBoost模型之间的R2、MAE和RMSE。首先,在所有缓冲区大小下,XGBoost模型都优于OLS回归模型。XGBoost模型将R2从0.10提高到0.19,MAE从2355.1降低到2723.5,RMSE从319.9降低到2472.2。
其次,与XGBoost模型相比,四种缓冲区大小下OLS模型的性能差异相对较小,最大R2区间约为0.05。然而,XGBoost模型显示出不同的趋势,其中不同的缓冲区大小确实影响模型的预测能力,最大的R2区间达到0.12。
第三,在四个缓冲区模型中,OLS和XGBoost模型都强调,与使用其他缓冲区大小的模型相比,包含600米缓冲区大小的模型具有更高的预测能力。这一观察为选择600m缓冲区作为预测站区地铁客流和站区周边发展的推荐选择提供了令人信服的案例。
2.自变量的相对重要性
建成环境和站点特征因素的共同贡献在不同缓冲区大小(见表4)之间存在差异。研究结果提供了两点启示。首先,在文献中经常被忽视的车站特征变量,确实在影响地铁客流量中起着关键作用,特别是线路和入口的数量以及车站年龄,它们构成了从周边地区捕获地铁客流量的基本和直接方式。相比之下,单个建成环境变量对地铁出行的影响是边际的,但几个建成环境变量对出行的综合影响可能很大。其次,研究结果表明,建成环境的影响与邻近地铁站点高度交互,在600m汇水区域内影响最大,这与模型在不同缓冲区的预测性能的研究结果一致。
在不同的缓冲区大小(见图3)下,单个建成环境因子的排名显示出异质性和不一致的结果。尽管最有影响的特征在不同的缓冲区大小模型中通常保持一致的排名,但影响较小的变量的排名显著波动。
研究结果表明,商业用地、容积率和土地利用多样性通常被推荐用于增强TOD,在600米半径范围内对地铁客流量显示出类似的影响。然而,当缓冲区尺寸超过600m时,它们对地铁客流的影响急剧减小。相反,商业用地和街道密度的重要性随着缓冲区规模的扩大而增加。同时,以街道网络为基础的空间连通性的积极影响在更大范围内更为明显。
3.自变量的非线性效应
图4展示了四个缓冲区尺度上的人口密度和就业密度的SHAP图。就人口密度而言,SHAP图显示,在0至3万人/km2范围内,人口密度与地铁乘客量之间呈反U型关系。一旦超过这一临界值,关系再次转为正相关,尽管有些分散,而且这种模式在所有四个缓冲区规模模型中都是一致的。在300m和600m模型中,就业密度与地铁客流量之间呈倒"V"型关系。然而,就业密度对地铁客流量的不利影响在800m和1000m模型中明显减弱。
图5给出了不同土地利用类型在4种缓冲区尺度下的SHAP图,可以看出,缓冲区大小对土地利用与地铁客流之间的非线性关系有重要影响。尽管以数量而不是密度来衡量,土地利用在四种不同的缓冲区大小之间表现出显著的波动。
图6说明了多样性、设计和目的地可达性变量的SHAP图。结果表明,缓冲区大小对建成环境与地铁站客流之间的关系有不同程度的影响。例如,街道密度对300 m和600 m缓冲区模型内的地铁客流量的影响是相对一致的,这可以通过更平坦的曲线来证明。然而,在600 m和1000 m模型中,街道网络的曲线变得波动和上升。公交站点和到CBD距离的SHAP图也证实了缓冲区大小可能会影响它们与地铁客流的细微关联。
图6 多样性、设计和目的地可达性变量的SHAP值图
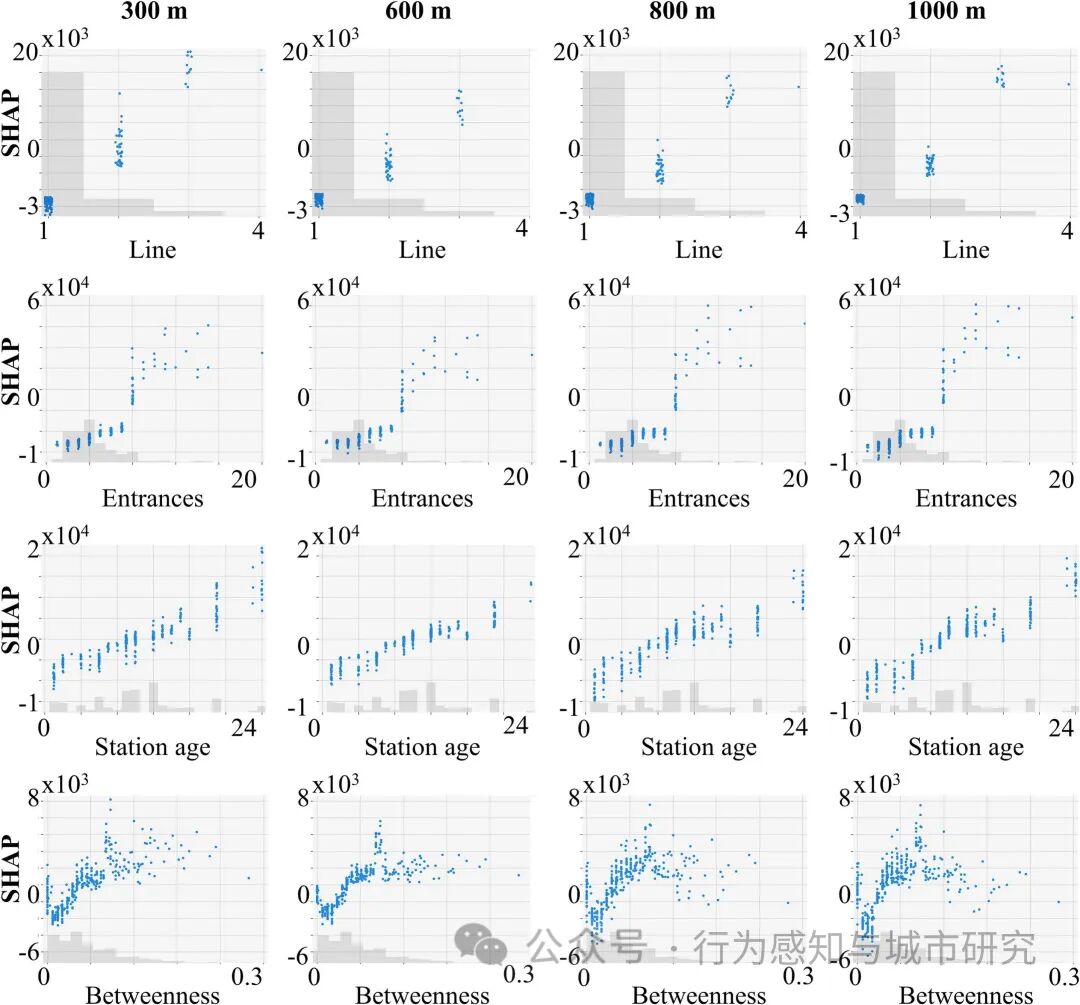
图7给出了台站特征变量的SHAP图。与建成环境变量相反,这些图表明缓冲区大小并不显著影响与地铁客流的相关性。