上篇文章:机器学习基本概念图解:线性回归和成本函数介绍了如何使用线性回归和成本函数来找到房价数据的最佳拟合线。然而,我们也发现,测试多个截距值可能既繁琐又低效。本篇将深入探讨梯度下降法,这是一种强大的技术,可以帮助我们找到最佳截距并优化模型。我们将探索其背后的数学原理,并了解如何将其应用于我们的线性回归问题。
梯度下降是一种强大的优化算法,旨在快速有效地找到曲线的最小值点。要形象地描述这个过程,最好的方式就是想象你站在山顶,山谷里有一个装满黄金的宝箱在等着你。
然而,由于天色昏暗,什么也看不见,你无法确定山谷的具体位置。而且,你也想抢在别人之前到达山谷(因为你想独吞所有宝藏,呵呵)。梯度下降可以帮助你探索地形,高效快速地到达这个最佳点。在每个点,它都会告诉你需要走多少步,以及应该朝哪个方向走。
类似地,梯度下降可以按照算法列出的步骤应用于我们的线性回归问题。为了直观地展示寻找最小值的过程,我们绘制MSE曲线。我们已经知道曲线的方程是:
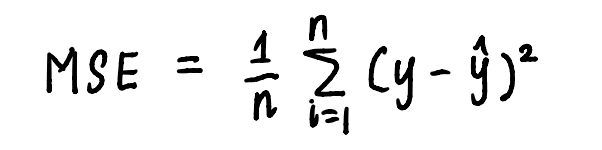
曲线方程是用于计算 MSE 的方程。
并且从上一篇文章中,我们知道我们的问题中的MSE方程是:

如果我们缩小图,我们可以看到,通过在上面的公式中代入一些截距值,可以找到一条MSE曲线(类似于我们的谷值)。因此,让我们代入 10,000 个
截距值,得到一条如下所示的曲线:
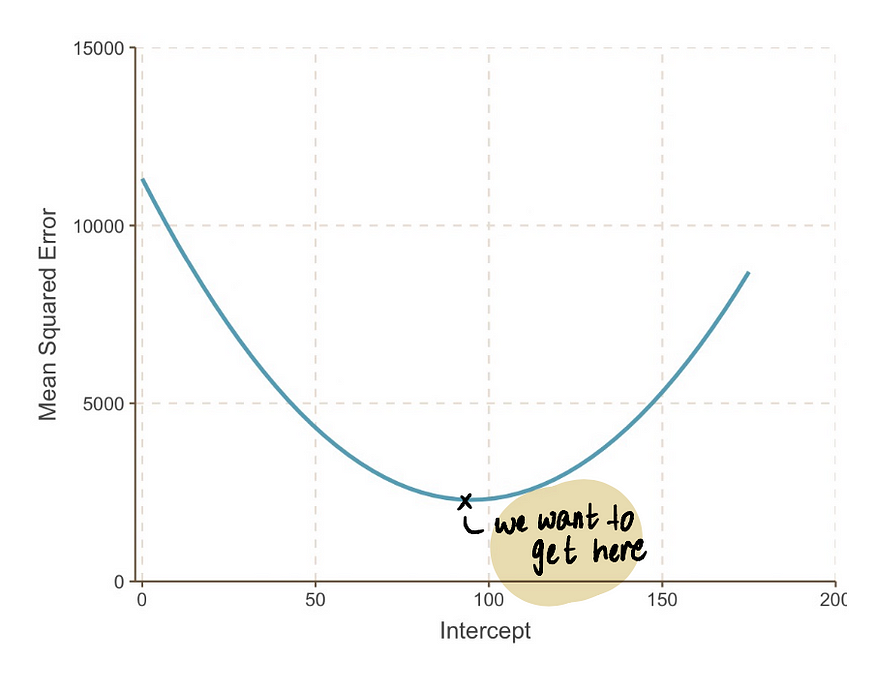
实际上,我们不知道 MSE 曲线是什么样子。我们的目标是达到MSE曲线的底部,我们可以按照以下步骤实现:
1.首先对截距值进行随机初始猜测
在这种情况下,我们假设截距值的初始猜测是 0。
2.计算该点的MSE曲线的梯度
曲线在某一点的斜率可以用该点处的切线(一种奇特的说法,表示该线仅在该点与曲线相切)表示。例如,在点 A,当截距等于 0 时, MSE曲线的斜率可以用红色切线表示。
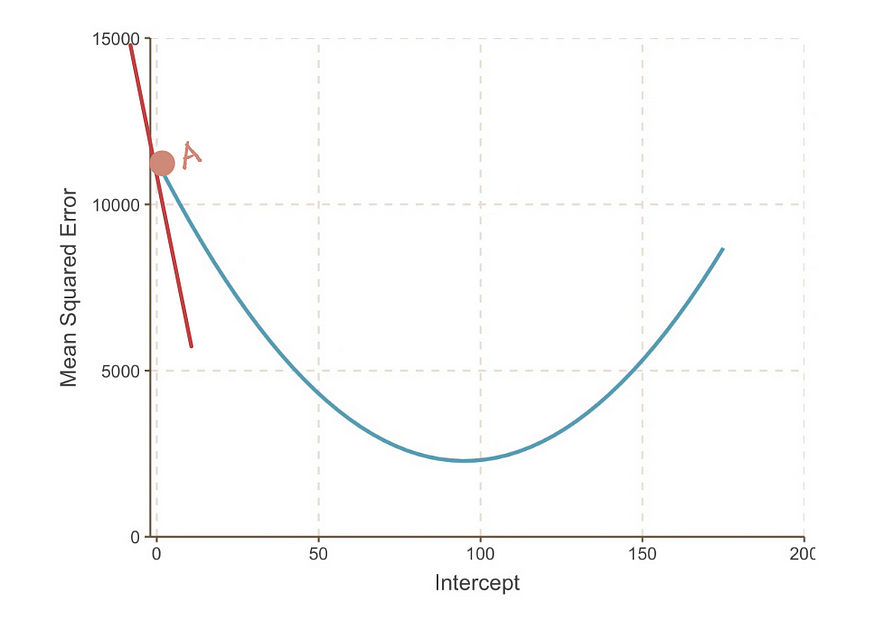
截距 = 0 时 MSE 曲线的梯度。为了确定梯度的值,我们运用微积分知识。具体来说,梯度等于曲线对给定点截距的导数。这表示为:
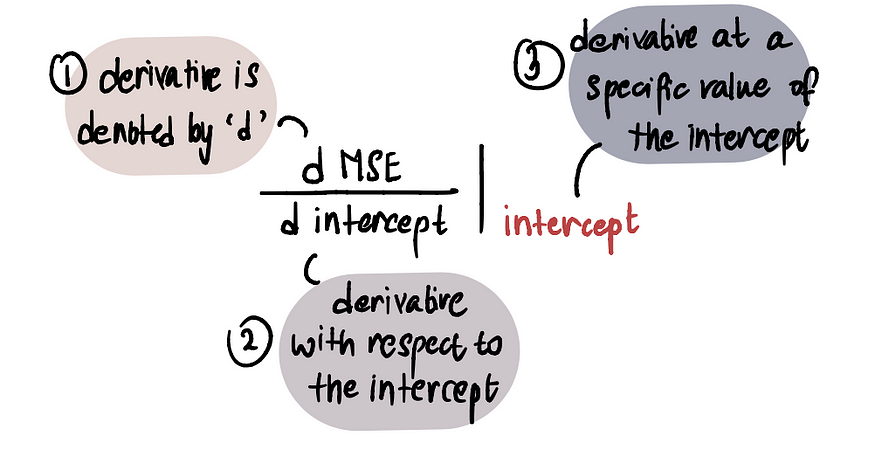
我们按如下方式计算MSE曲线的导数 :
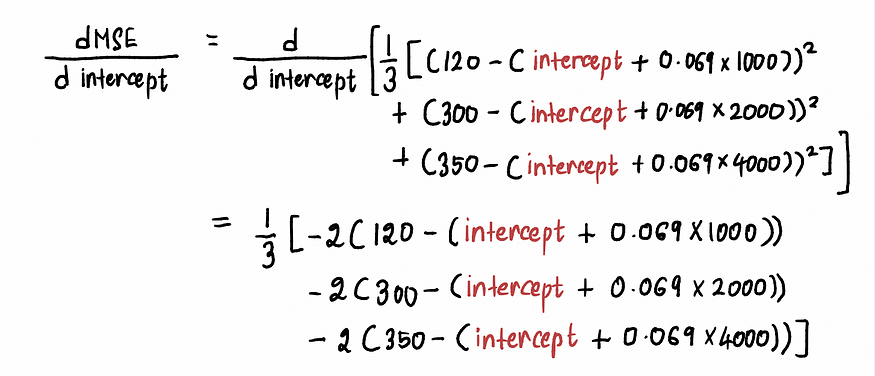
现在要求A 点处的梯度,我们将 A 点处的截距值代入上式。由于截距= 0,A 点处的导数为:
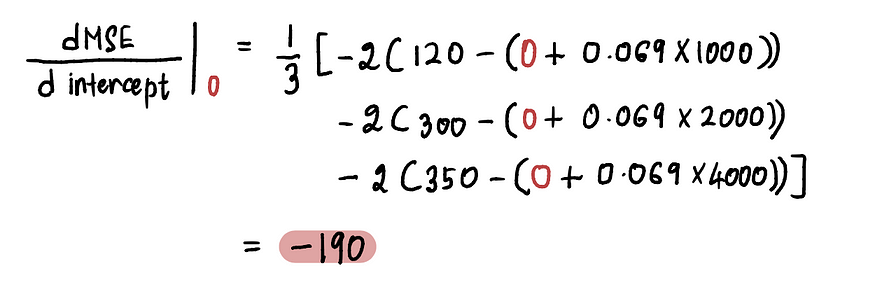
因此,当截距= 0 时,梯度= -190。
注意:当我们接近最优值时,梯度值会趋近于零。在最优值处,梯度等于零。相反,我们离最优值越远,梯度就越大。
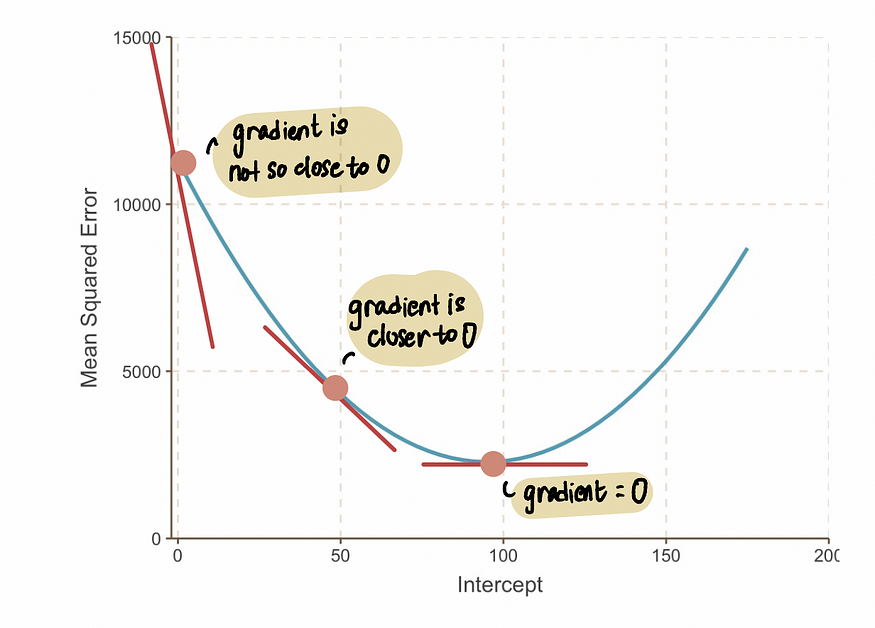
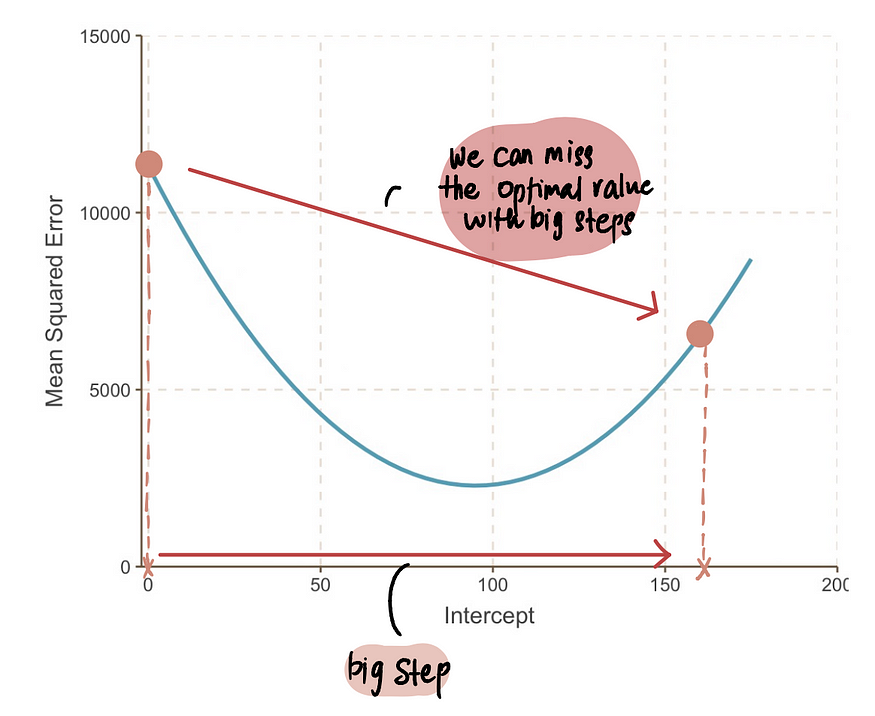
由此,我们可以推断,步长应该与梯度相关,因为它告诉我们应该小步走还是大步走。这意味着,当曲线的梯度接近于 0 时,我们应该小步走,因为我们已经接近最优值了。而如果梯度较大,我们应该采取更大的步长,以便更快地达到最优值。
注意:但是,如果我们迈出超大的一步,那么我们可能会跳跃过大而错过最佳点。所以我们需要小心。
3.使用梯度和学习率计算步长并更新截距值
因为我们看到
步长和坡度彼此成比例,步长乘以坡度由一个预先确定的常数值称为学习率:

学习率控制步长的大小,并确保所采取的步长不会太大或太小。
实际应用中,学习率通常是一个小于等于 0.001 的正数。但对于我们的问题,我们将其设置为 0.1。
因此当截距为 0 时:
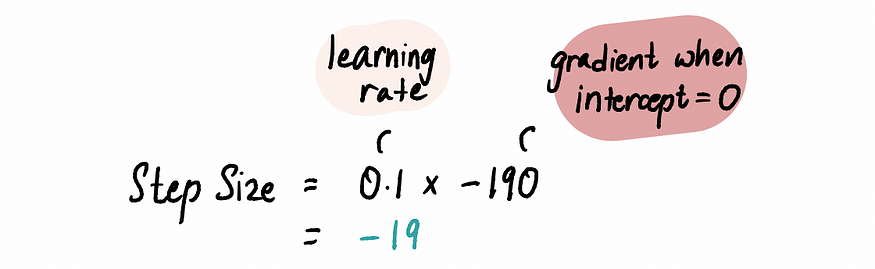
根据上面计算的步长,我们使用以下任何等效公式来更新截距(即改变我们当前的位置) :

为了在此步骤中找到新的截距,我们代入相关值,并发现新的截距= 19。
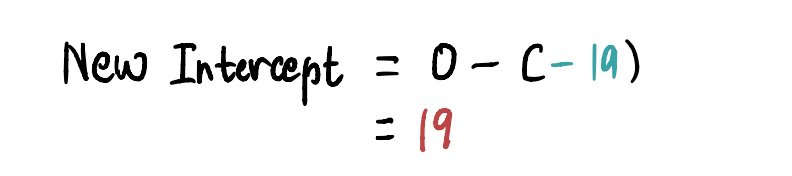
现在将这个值代入MSE方程,我们发现截距为 19时的MSE = 8064.095。我们迈出了一大步,更接近了最优值,并降低了MSE。
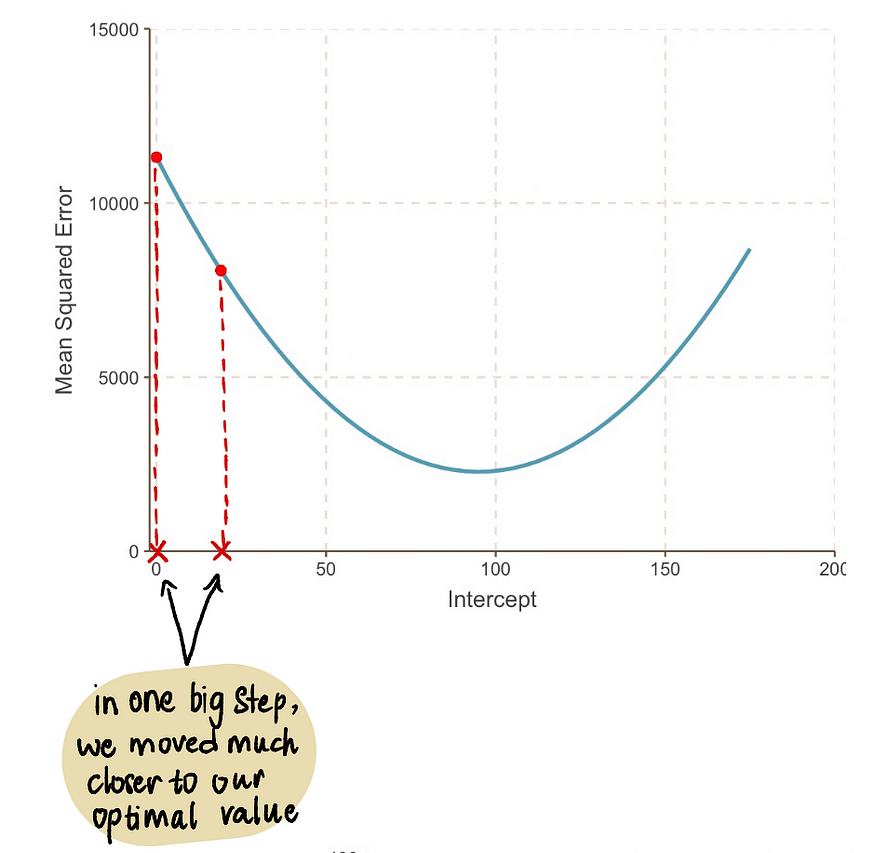
即使我们看一下图表,我们也会发现截距为 19 的新线比截距为 0 的旧线更适合我们的数据:
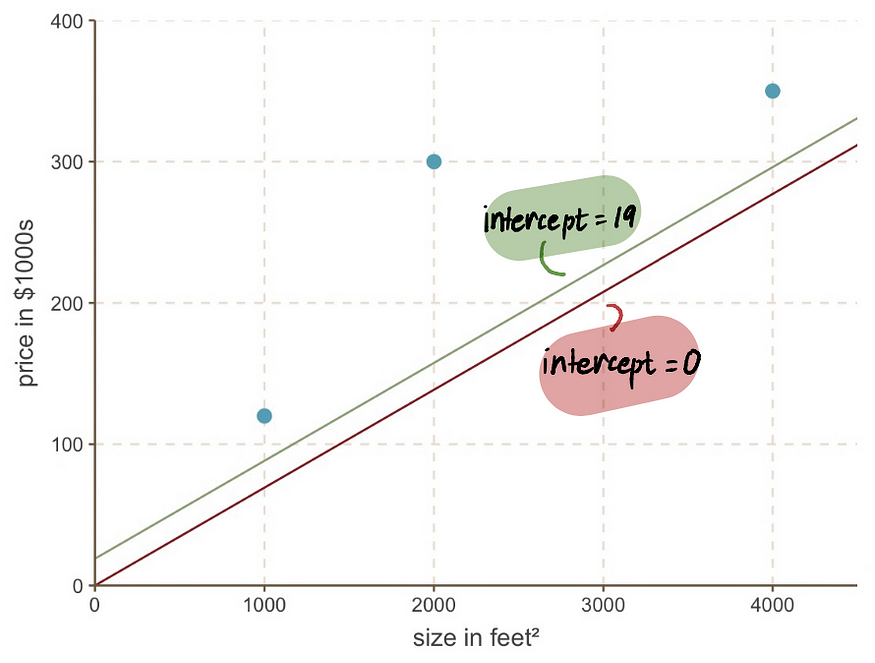
4.重复步骤 2-3
我们使用更新后的截距值重复步骤 2 和 3 。例如,由于本次迭代中的新截距值为 19,按照步骤 2,我们将计算此新点的梯度:
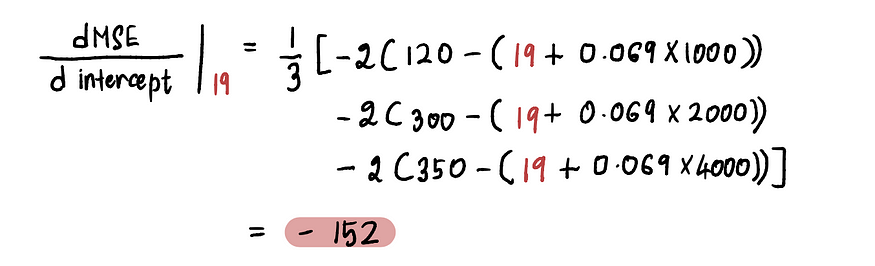
我们发现,截距值为 19 处的MSE曲线的斜率是 -152(如下图中红色切线所示)。
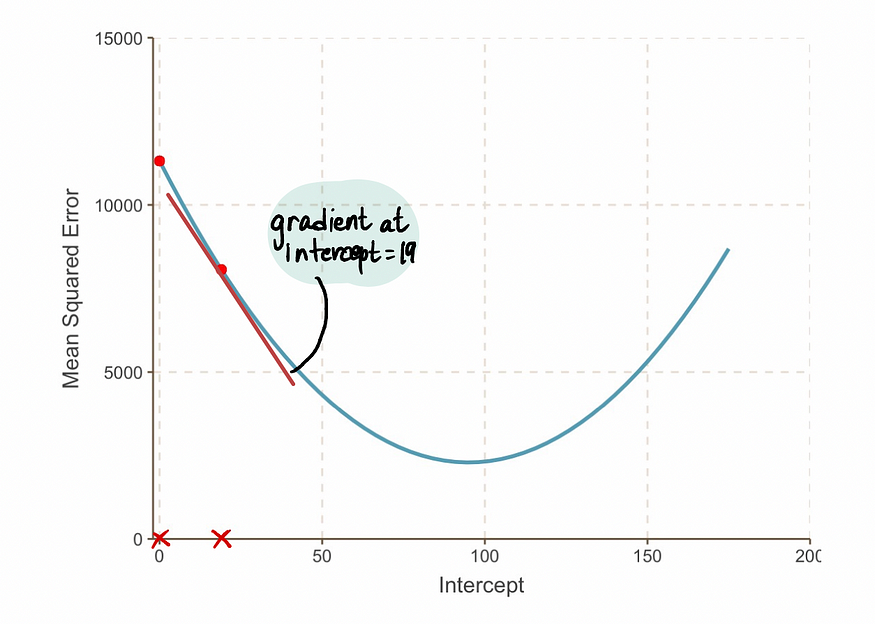
接下来,按照步骤 3
,我们来计算步长:
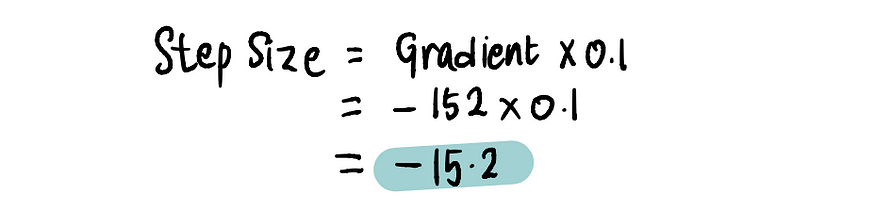
然后更新截距值:
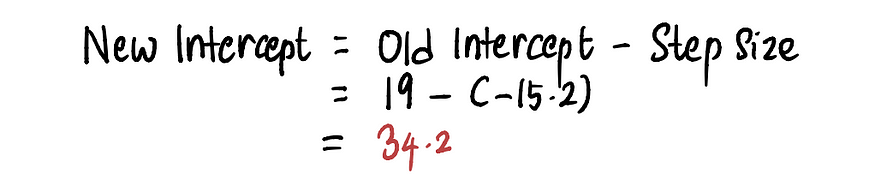
现在我们可以将之前的截距为 19 的线与新的截距为 34.2 的线进行比较。
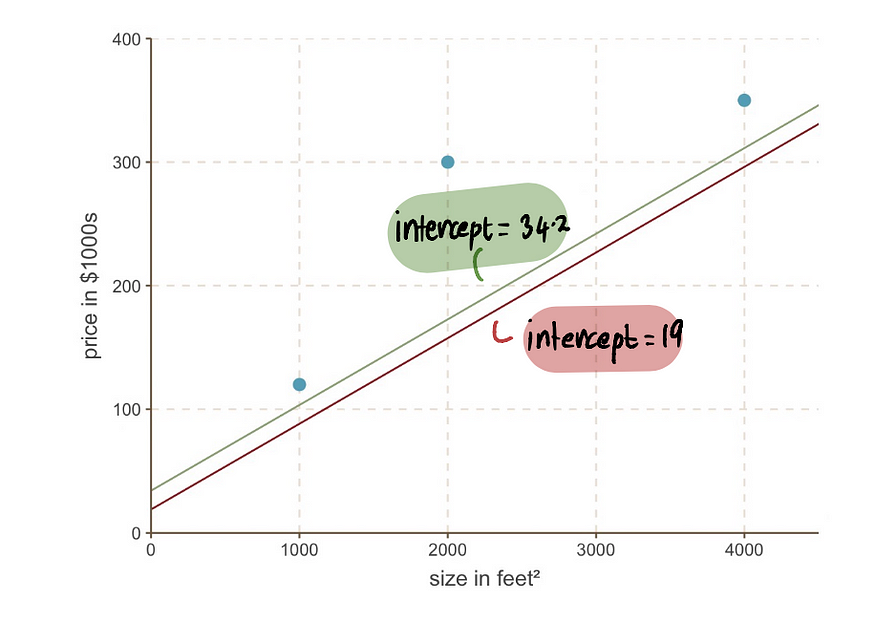
我们可以看到新线更适合数据。总体而言,MSE正在变得越来越小。
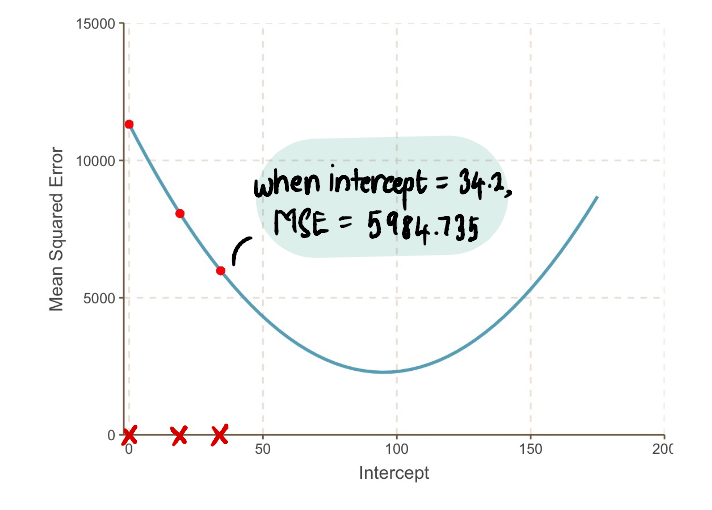
我们的步长越来越小:
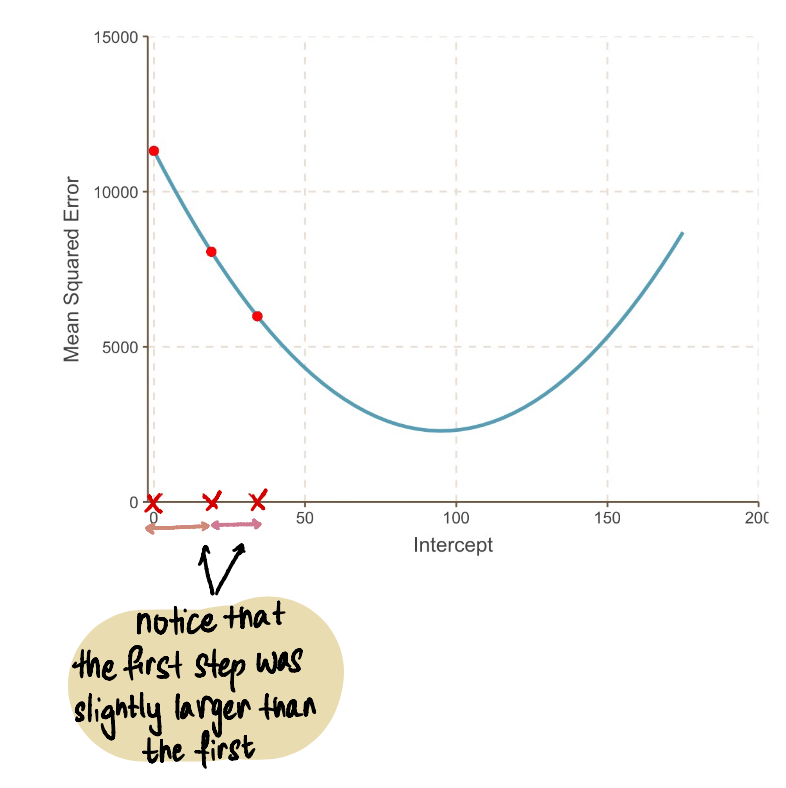
我们反复重复这个过程,直到找到最优解:
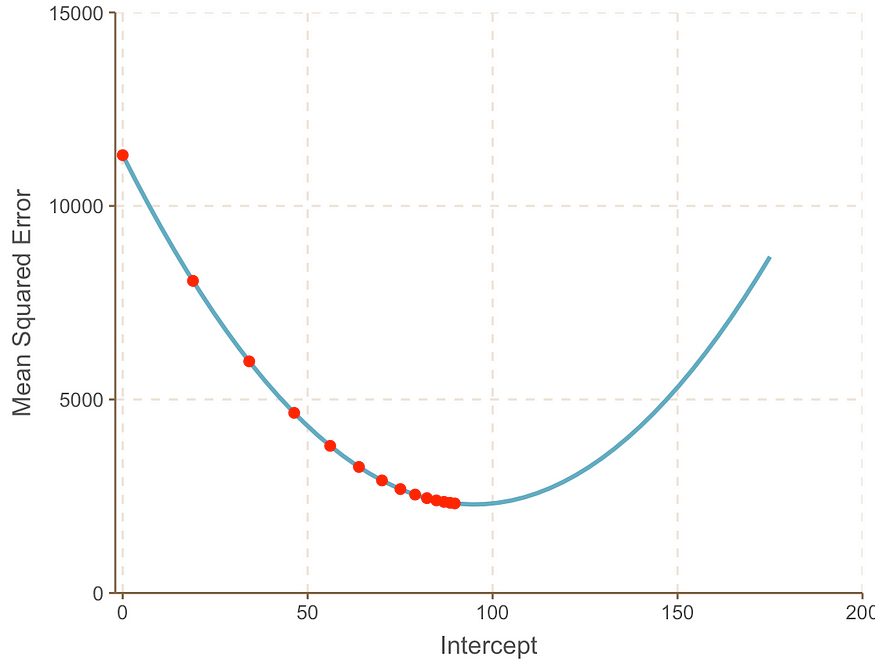
随着我们接近曲线的最小值点,我们观察到步长变得越来越小。经过13步后,梯度下降算法估计截距值为95。如果我们有一颗水晶球,这将被确认为MSE曲线的最小值点。并且,与我们在上一篇文章中看到的蛮力方法相比,这种方法显然更加高效。
现在我们有了截距的最优值,线性回归模型是:

线性回归线如下所示:
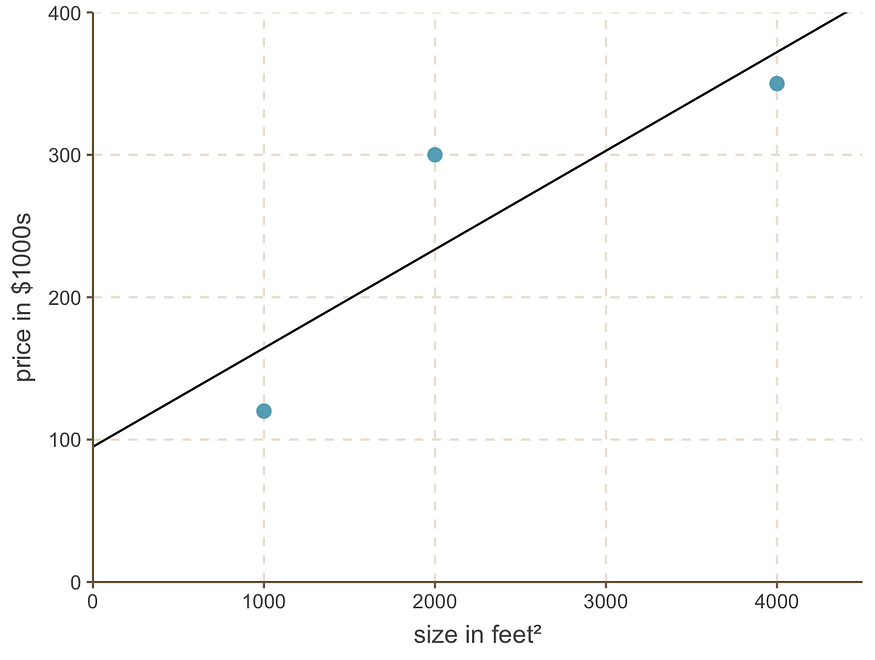
最佳拟合线,截距 = 95,斜率 = 0.069
最后,回到我们的朋友马克的问题——他应该以什么价格出售他的 2400 平方英尺的房子?

将房屋面积 2400 平方英尺代入上述等式中……
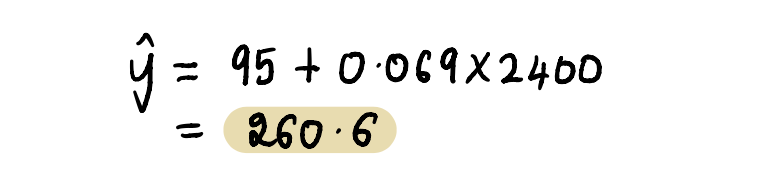
根据他家附近这三栋房子的情况,他应该以 260,600 美元左右的价格出售这栋房子。
现在我们已经对这些概念有了深入的理解,让我们做一个快速的问答环节来回答任何遗留的问题。
为什么找到梯度实际上有效?
为了说明这一点,考虑这样一个场景:我们正试图到达曲线 C 的最小值点,记为x*。我们当前位于x处的点 A ,位于x*的左侧:
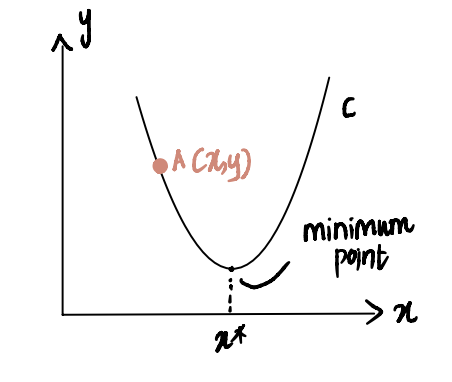
如果我们对点 A 处的曲线求导,表示为
dC (x)/dx,则会得到一个负值(这意味着梯度向下倾斜)。我们还观察到,我们需要向右移动才能达到x*。因此,我们需要增加x才能达到x*的最小值。
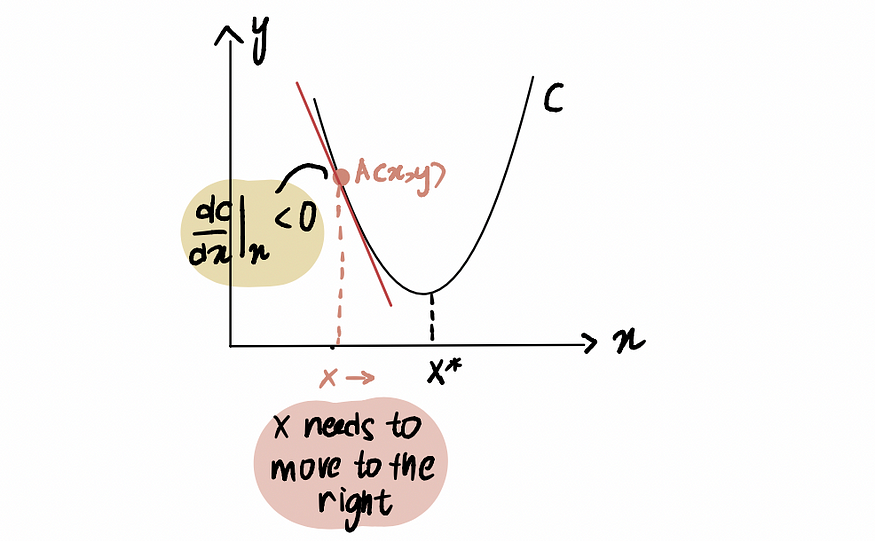
红线(或梯度)向下倾斜 => 负梯度
由于dC(x)/dx为负,因此x-𝛂*dC(x)/dx将大于x ,从而向x*移动。
类似地,如果我们位于最小点 x* 右侧的点 A,那么我们得到一个正梯度(梯度向上倾斜),dC(x)/dx。
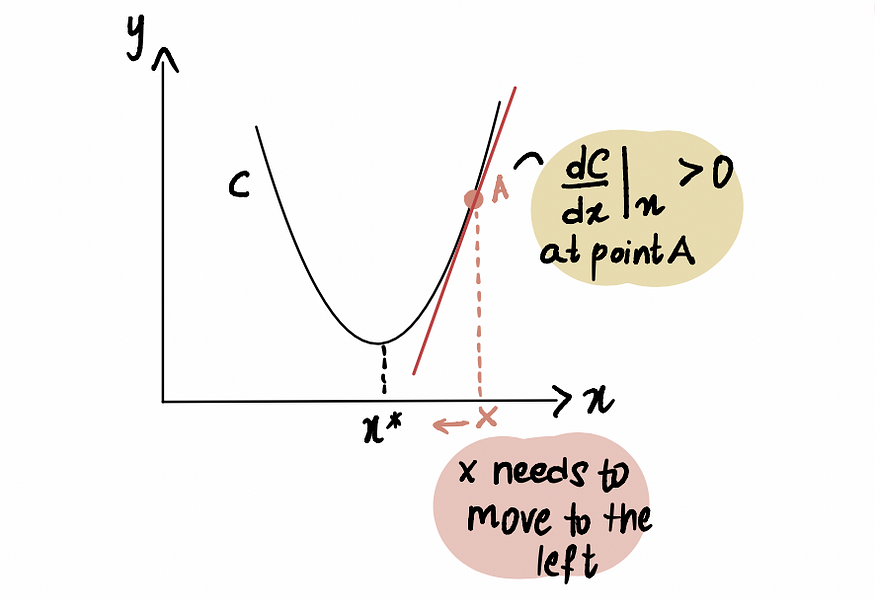
红线(或梯度)向上倾斜 => 正梯度
因此x-𝛂*dC(x)/dx将小于x,从而趋向x*。
梯度下降如何知道何时停止采取措施?
当步长 (Step Size)非常接近 0时,梯度下降停止。如前所述,在最小值点处梯度为 0,而当我们接近最小值时,梯度会趋近于 0。因此,当某点处的梯度接近于 0 或在最小值点附近时,步长 (Step Size)也会接近于 0,这表明算法已经达到最优解。
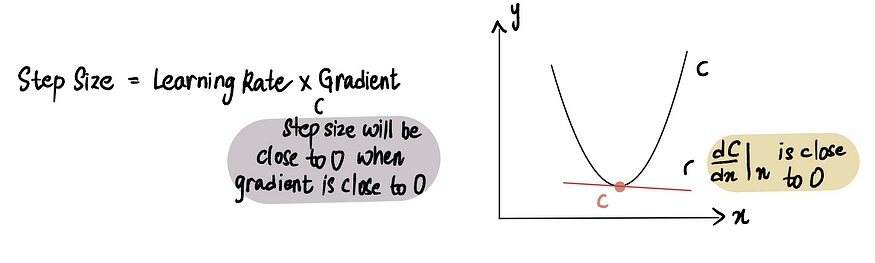
当我们接近最小值点时,梯度接近于 0,随后,步长也接近于 0
实际上,最小步长 = 0.001 或更小
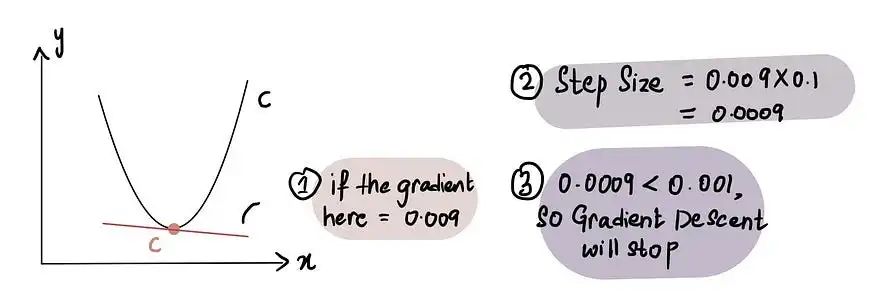
话虽如此,梯度下降还包括放弃之前所采取的步数的限制,称为最大步数。
实际上,最大步数 = 1000 或更大
因此,即使步长大于最小步长,如果步数已超过最大步数,梯度下降就会停止。
如果最小点更难识别怎么办?
到目前为止,我们一直在处理容易识别最小值点的曲线(这类曲线称为凸曲线
)。但是,如果我们有一条不那么漂亮的曲线(技术上称为非凸曲线),看起来像这样,该怎么办?
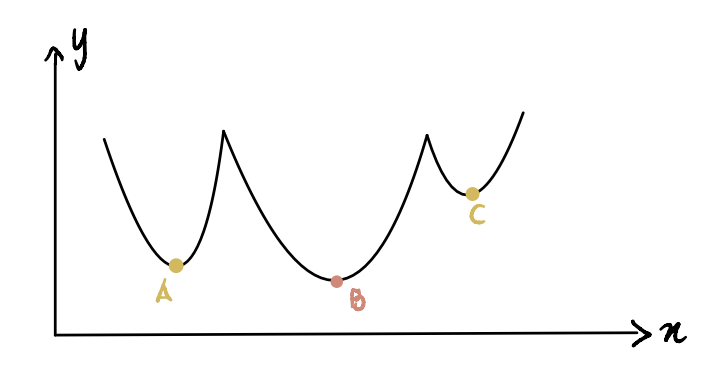
在这里,我们可以看到点 B 是全局最小值(实际最小值),点 A 和 C 是局部最小值(可能被误认为是全局最小值但实际上并非如此)。因此,如果一个函数有多个局部最小值和一个全局最小值,梯度下降法并不能保证一定能找到全局最小值。此外,它找到哪个局部最小值取决于初始猜测的位置(如梯度下降法第一步所示)。
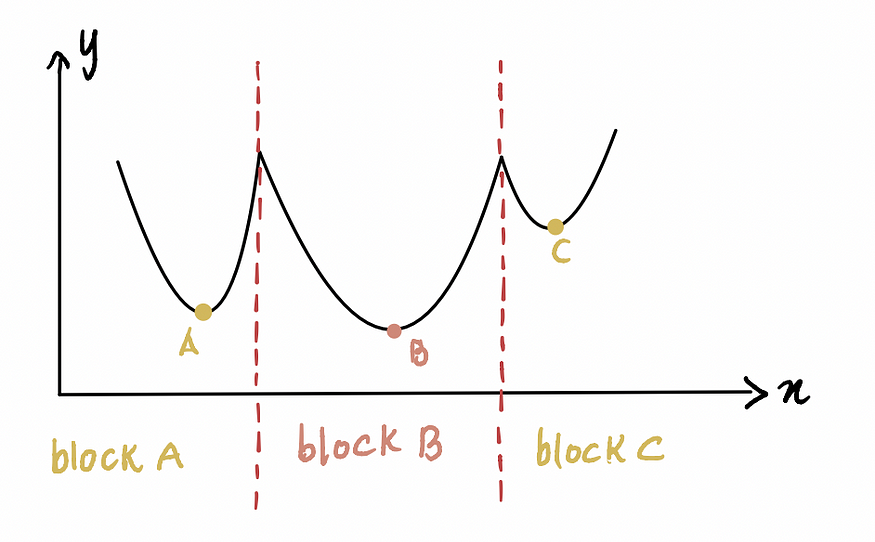
以上面这个非凸曲线为例,如果初始猜测在区块 A 或区块 C,梯度下降将声明最小值点分别位于局部最小值 A 或 C,而实际上它位于 B。只有当初始猜测在区块 B 时,算法才会找到全局最小值 B。
现在的问题是——我们如何做出正确的初步猜测?
答案很简单:尝试并犯错。有点儿像。
答案并不那么简单:从上图可以看出,如果我们对x的最小猜测为 0(因为它位于区块 A),那么它将导致局部最小值 A。因此,正如您所见,在大多数情况下,0 可能不是一个好的初始猜测。一种常见的做法是将一个基于均匀分布的随机函数应用于 x 所有可能值的范围。此外,如果可行的话,使用不同的初始猜测运行算法并比较它们的结果,可以深入了解这些猜测之间是否存在显著差异。这有助于更有效地识别全局最小值。
好的,我们快到了。最后一个问题。
如果我们试图找到多个最优值怎么办?
到目前为止,我们只专注于寻找最佳截距值,因为我们神奇地知道线性回归的斜率值是 0.069。但是,如果我们没有水晶球,不知道最佳斜率值怎么办?那么我们需要同时优化斜率和截距值,分别表示为x₀和x₁。
为了做到这一点,我们必须利用偏导数,而不仅仅是导数。
注意:偏导数的计算方法与常规导数相同,但由于我们要优化的变量不止一个,因此其表示方式有所不同。想了解更多信息,请阅读这篇文章或观看此视频。
然而,这个过程与优化单个值的过程相对相似。仍然需要定义成本函数(例如MSE),并且必须应用梯度下降算法,但增加了对 x₀ 和 x₁ 求偏导数的步骤。
步骤 1:对 x₀ 和 x₁ 进行初步猜测
步骤 2:求出这些点处关于 x₀ 和 x₁ 的偏导数
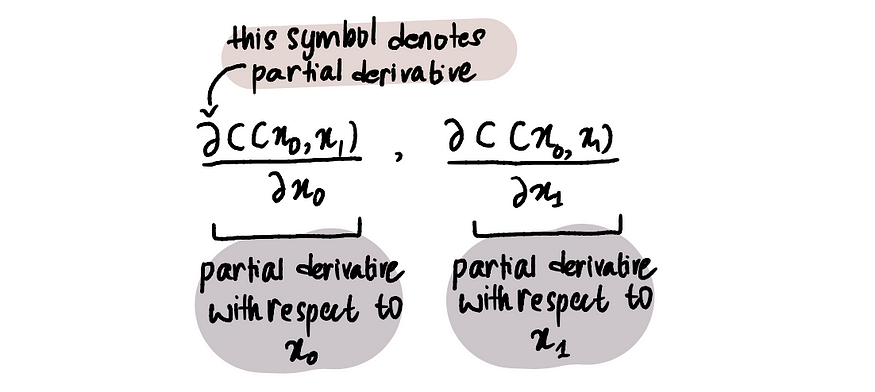
步骤 3:根据偏导数和学习率同时更新 x₀ 和 x₁
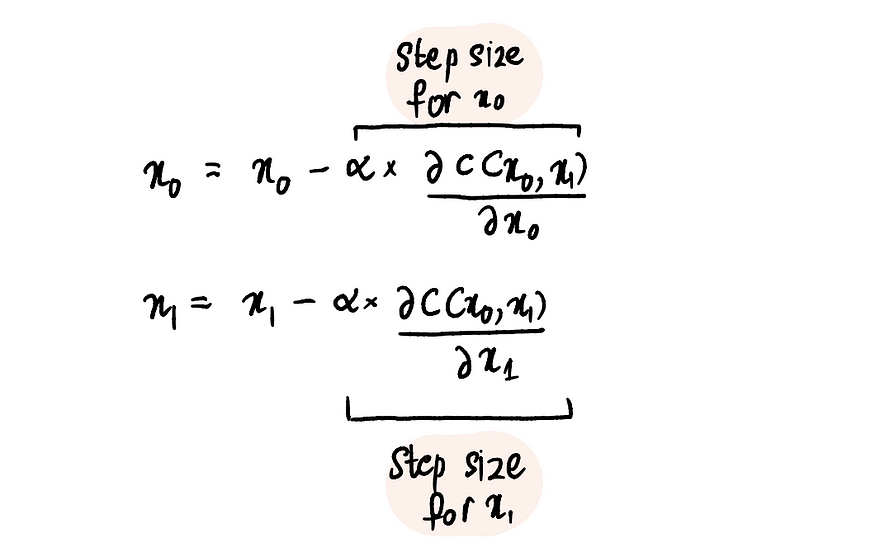
步骤 4:重复步骤 2-3,直到达到最大步数或步长小于最小步长
我们可以将这些步骤推断为 3、4 甚至 100 个值以进行优化。
总而言之,梯度下降是一种强大的优化算法,能够有效地帮助我们达到最优值。它可以应用于许多其他优化问题,使其成为数据科学家必备的基本工具。
原文:https://medium.com/data-science/back-to-basics-part-uno-linear-regression-cost-function-and-gradient-descent-590dcb3eee46