一图搞懂深度学习 - 基于梯度的优化（梯度下降）

在模型优化过程中，我们曾尝试通过手动调整单个标量系数来观察其对损失值的影响。具体来说，当初始系数为0.3时，损失值为0.5。随后，我们尝试增加系数至0.35，发现损失值上升至0.6；相反，当系数减小至0.25时，损失值下降至0.4。这一实验结果表明，在该特定情境下，减小系数值有助于降低模型的损失值。

然而，这种方法在实际应用中非常低效，因为模型通常包含大量的系数（可能达到上千个甚至上百万个），对每个系数进行两次前向传播来计算不同取值下的损失值，计算成本极高。

为了解决这个问题，引入了梯度下降法作为一种更高效的优化方法。梯度下降法通过计算损失函数对每个系数的梯度（即损失值对系数的导数），能够指导我们如何调整每个系数以最小化损失值，而无需对每个系数进行多次前向传播试验。

1. 初始化参数：选择一个起始点作为初始参数，这些参数可以是任意值或随机选择的值。

2. 计算梯度：计算当前参数点处的损失函数的梯度。梯度是一个向量，表示损失函数在每个参数维度上的变化率。

3. 更新参数：使用梯度信息来更新参数，以使损失函数的值减小。这通常是通过沿着梯度的反方向进行调整来实现的，调整的大小由学习率决定。

4. 迭代更新：重复计算梯度和更新参数的步骤，直到满足停止准则，如达到预设的最大迭代次数或损失函数值减小到足够小的值。

1. 批量梯度下降（Batch Gradient Descent，BGD）：在每次迭代中使用全部的训练数据来计算梯度，然后更新模型参数。

• 优点：收敛速度相对较快，可以利用矩阵运算加速计算，且在凸优化问题中能保证收敛到全局最优解。

• 缺点：在处理大规模数据集时，计算梯度的时间和空间复杂度较高，内存使用量可能过大。

2. 随机梯度下降（Stochastic Gradient Descent，SGD）：在每次迭代中随机选择一个样本来计算梯度，然后更新模型参数。

• 优点：计算梯度的时间和空间复杂度较低，适用于处理大规模数据集，且能跳出局部最优解（因为每次更新参数的方向不一定是相同的）。
• 缺点：收敛速度较慢，且可能会出现震荡现象，对于稠密数据集的计算速度可能较慢。

• 优点：计算梯度的时间和空间复杂度较低，收敛速度较快，且可以利用矩阵运算的并行性加速计算，同时能跳出局部最优解。

• 缺点：需要手动设置小批量大小，如果选择不当可能会影响收敛速度和精度。对于大规模、稀疏或实时数据流问题，其计算效率可能不如SGD，但比BGD要好。

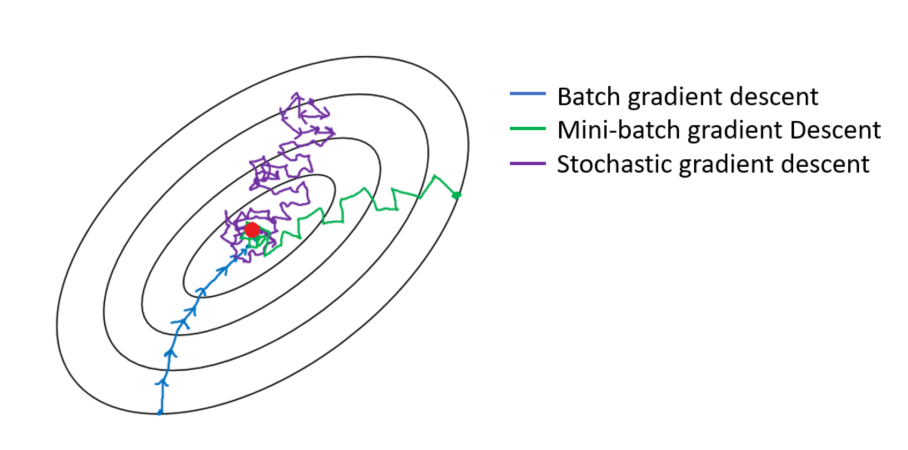
“一图 + 一句话”彻底搞懂BGD、SGD、MBGD。