附件内容摘录

A.1 数据预处理

我们使用结构化查询语言（SQL）从医院信息系统（HIS）中检索并构建数据库，相关代码已通过临床专家和数据库工程师的审核。采用随机抽样策略，将提取的数据与患者的扫描病历进行交叉核对，并根据抽样结果调整检索策略。同时，利用相关的流行病学调查、高质量随机对照试验（RCT）和队列研究对数据进行二次验证。

本研究首先使用227个心脏手术国际疾病分类（ICD）代码筛选研究对象。为进一步验证纳入患者的准确性，我们通过识别手术名称中的关键词（共78项）对患者进行细致评估。此外，通过仔细核查患者住院期间的计费记录，我们确定了289项与目标人群特定手术及耗材费用相关的项目，用于对研究人群进行进一步验证和交叉核对。

为确保20多年来来自多个医疗中心患者数据的准确性和一致性，我们根据样本来源、测量单位和参考范围，对相同实验室检查结果的检测项目进行了细致的合并与标准化处理。我们对不同的检测名称、单位和检测试剂盒进行比对和转换，以确保含义一致。

此外，我们还进行了异常值检测与修正，以保障数据准确性。首先，基于医学常识识别输入错误并采取纠正措施；其次，构建与数据相关的新变量，对数据进行进一步核查和修正；同时，采用多元高斯分布等机器学习异常值检测方法，对结构化数据进行处理和检验。

为确保数据的可靠性和有效性，我们整合了ICD-9和ICD-10疾病代码，并结合自然语言处理工具与人工验证，对对于多次入院的患者，我们患者的既往病史进行进一步处理。将每次入院视为一个独立的数据样本。排除缺少基线（术前）血清肌酐或术后血清肌酐检测值的患者；若最新术前血清肌酐检测时间距手术超过90天，则将该基线标记为缺失，并将该病例排除在分析之外；同样，住院时长超过90天的病例也视为异常值并予以剔除。

时序数据构建

为实现心脏手术相关急性肾损伤（CSA-AKI）的动态实时预警，我们将预处理后的数据转换为时间结构化序列。将患者的住院数据（包括生命体征和实验室检查结果）按时间顺序排列，构建间隔为2小时的时序数据。实验室检查（如肌酐、尿素氮等）在临床确定的时间点进行检测。

模型的输入为每个变量的时间序列，每产生一项新的实验室检查结果，都会按其检测时间戳添加到对应序列中。预测过程具有“实时性”，即实验室检查结果一旦可用便会被纳入模型。这种变量的动态使用方式是该模型的优势之一，能够实现风险的持续更新。

尽管2小时的采样间隔会导致部分检测频率较低或不规律的变量出现时间空白段，但我们的模型通过指示变量明确体现数据缺失情况，从而以统一的方式处理不规律且低频率的记录，确保其在不同医院间具有较高的适用性。

数据插补

部分数据的缺失可能并非随机（例如，对于病情稳定的患者，临床医生可能不会开具特定的实验室检查，导致相关数据缺失）。因此，我们没有采用传统的数据插补方法，因为我们认识到数据缺失本身可能反映患者的病情稳定状态。相反，我们通过缺失指示变量明确表示缺失数据，以保留这一具有信息价值的信号。

对于在同一时间窗口内被多次测量的指标，我们计算其平均值来代表患者在该时间段内的状态。此外，我们还系统地识别并修正了数据点之间不合理的时间间隔。

AKI的定义与标注

本研究中，心脏手术相关急性肾损伤（CSA-AKI）的定义采用改良的肾脏病：改善全球预后（KDIGO）标准：

• I期（轻度）：48小时内血清肌酐升高≥0.3mg/dL，或血清肌酐升高至基线值的1.5-1.9倍（且推测该升高发生在过去7天内）；
• II期（中度）：血清肌酐升高至基线值的2.0-2.9倍；
• III期（重度）：血清肌酐升高至基线值的3.0倍及以上、血清肌酐升高至≥4.0mg/dL，或启动肾脏替代治疗。

此外，我们还结合国际疾病分类（ICD）代码中临床医生诊断的AKI，对AKI的定义进行补充。我们未采用从原始电子健康记录（EHR）中提取的直接尿量数据，原因如下：（1）心脏手术患者常通过容量扩张和利尿剂调整液体平衡，在此背景下尿量并非可靠指标；（2）心脏重症监护室的液体管理策略差异极大，受患者个体差异和主管医生诊疗偏好的影响[1-4]。

我们根据上述分类定义每个时间间隔内患者的当前状态，并将随后48小时的状态作为标签。考虑到AKI的进展性， 我们设定了12个预测目标，重点预测未来6、12、24和48小时内三类CSA-AKI（所有AKI、中重度AKI、重度AKI）的发生情况。动态变化的预测窗口（如0-6小时、0-12小时等）自手术后立即开始，例如，6小时预测窗口用于判断从当前时刻起6小时内是否会发生AKI。此外，AKI分期采用患者近期的肌酐检测值进行动态分类，而非长期（如住院期间）的肌酐峰值。

对于每个预测时间点（发病前t小时），模型输入仅包含截至该时间点可获取的数据。预测时间戳之后的所有实验室检查值（包括肌酐）均被严格屏蔽并排除，模型不会获取任何未来（t时刻之后）的信息。若患者在规定的观察期和预测窗口内未进行肌酐检测，则该预测样本被标记为标签模糊，并从训练集和评估集中剔除，以避免因缺乏检测而将患者误分类为“非AKI”。

本研究的主要结局指标是预测发病前6-48小时内重度（III期）CSA-AKI的发生情况。我们将重度AKI（III期）设为主要结局指标，是因为其会带来最严重的临床后果（如需要透析治疗、高死亡率），且通常需要最紧急的干预。相比之下，轻度AKI（I期）可能是暂时性的，影响较小。因此，早期识别重度AKI高危患者具有极高的临床价值。为确保模型的广泛适用性，我们仍将轻度AKI的预测结果作为次要结局指标，对模型性能进行评估。

模型评估

采用布里尔评分（Brier Score，即预测概率的均方误差）和校准曲线对模型的校准度进行评估。布里尔评分用于量化二分类事件的预测准确性，其计算公式为：

其中， 为预测概率， 为实际结局（0或1）， 为预测次数。布里尔评分越低，表明模型的校准效果越好。

A.3 因果深度学习相关概念

深度学习中的因果性

因果性是深度学习领域一个新兴的研究方向。它通过挖掘复杂分布中隐藏的因果关系，降低深度学习模型出现数据驱动型错误的可能性，同时确保模型在不同环境下的稳定性和可解释性。

以训练神经网络区分猫和狗为例：由于许多狗的图片中，狗都处于草地上，模型可能会通过判断“动物是否在草地上”来识别狗。但这种预测方式并不稳定，因为存在大量狗不在草地上的图片[5]。这一问题同样存在于医疗结局预测场景中，例如心脏手术相关急性肾损伤（CSA-AKI）的预测。若仅依靠患者年龄进行预测，当年轻患者因其他原因发生CSA-AKI时，模型就可能出现预测错误，因此这种预测方式稳定性较差。

相反，若基于导致结局的风险因素进行预测[6]——例如，通过观察耳朵、鼻子等特征识别狗，通过导致CSA-AKI的实际病因预测CSA-AKI——深度学习模型在不同环境下的泛化能力会显著提升。

结构因果模型（SCM）

通过考虑时空结构依赖性，时序数据中的因果关系可通过结构因果模型（SCM）[7]来表示。我们将均匀采样的时序数据记为 ，其中为时刻 的样本向量，包含个变量，且。这里，代表患者编号，代表该患者时序数据的长度。

时序数据的结构因果模型（SCM）[8]可表示为：（）。其中，是代表时空结构依赖性的（潜在）非线性函数；代表潜在变量（也可视为噪声）；代表变量的“因果父集”（即对有直接因果影响的变量集合）。

因果发现（同时也是我们因果深度学习方法）的核心任务，就是为每个变量识别出其对应的因果父集。在A.4节中，我们将简要介绍现有的因果发现方法。

非线性格兰杰因果性

格兰杰因果性是因果发现的一大类核心方法。我们将输入数据集记为（为简化分析，此处将所有输入数据均视为时序数据；对于年龄、性别等静态变量，我们假设CSA-AKI对这些变量无因果影响，这一假设同样符合格兰杰因果性的前提）。其中，代表第位患者的第条时序数据，（为患者总数），（为每位患者的时序变量总数）。

本文采用现有研究[9,10]中的表示方法，将标签的预测概率定义为：

其中，，（为类别总数）。本文重点研究从输入到标签的因果关系发现。

在动态系统中，若时序数据的历史值有助于预测标签的未来状态，则称时序数据对未来结局存在格兰杰因果影响。标准的格兰杰因果性适用于线性关系场景，近年来已被扩展到非线性关系场景[11]，其定义如下：

定义1：当且仅当存在类别和不同于的，使得

时，时序数据对结局存在格兰杰因果影响。
也就是说，时序数据的历史数据会影响对的预测结果。

非线性格兰杰因果性与神经网络（NN）具有高度兼容性。考虑到神经网络的通用逼近能力[12]，我们可通过分量级多层感知机（MLP）或循环神经网络/长短期记忆网络（RNN/LSTM）来拟合因果关系函数。此外，如文献[10,13]所述，通过对网络连接权重施加稀疏正则化，神经网络能够学习所有个变量与预测标签之间的因果关系。

需要注意的是，格兰杰因果性并不等同于“真正的因果性”（即珀尔（Pearl）所定义的因果性），但研究证明，在假设“无即时效应”和“无潜在混杂变量”的前提下，格兰杰因果性可支持因果结论的推导[14]。近年来，由于格兰杰因果性能够发现目标变量的因果父集[15]，已被广泛应用于各类场景。但若存在未被测量的混杂变量，可能导致虚假因果结论的产生，因此对相关结果的解读需保持谨慎。

A.4 因果发现相关研究进展

我们的方法通过识别因果关系，使心脏手术相关急性肾损伤（CSA-AKI）预测模型能在不同环境下泛化，这一过程与因果发现领域密切相关。因果发现（又称因果结构学习）涵盖静态场景与动态时序场景，是机器学习领域近几十年来的研究热点，并已取得显著进展。我们将现有因果发现方法大致分为以下几类：

基于约束的方法

此类方法（如PC算法[16]、FCI算法[17]）通过执行条件独立性检验构建因果图。后续该类方法被扩展到时序场景中，典型代表包括时序FCI算法（tsFCI）[18]和PCMCI算法[8,19,20]。

基于评分的学习算法

这类算法通过应用带惩罚项的神经常微分方程或无环约束来重构因果图[21,22]。

加性噪声模型（ANM）

加性噪声模型基于加性噪声假设推断因果图[23]，其适用前提包括：数据生成过程为线性、无未观测混杂变量、扰动变量服从非零方差的非高斯分布。文献[24]将加性噪声模型扩展到非线性场景，使其可适用于几乎所有非线性形式与加性噪声结合的模型。

基于格兰杰因果性的方法

格兰杰因果性由文献[25]首次提出，该方法通过检验某一时序数据对另一时序数据预测的辅助作用，分析两者间的时间因果关系。近年来，深度神经网络（NN）被广泛应用于非线性格兰杰因果发现[9,10,13,26-28]。

收敛交叉映射（CCM）

收敛交叉映射由文献[29]提出，可用于为不可分离的弱连接动态系统重构非线性状态空间。后续该方法被扩展到同步、混杂或零散时序等场景[30-32]。

A.5 REACT的两阶段框架

在本文中，我们提出一种方法，可实现：

• a）识别对目标结局存在因果影响的变量；
• b）利用识别出的因果变量预测结局。

这两个阶段协同进行、相互促进。在下文部分，我们将分析因果发现为何有助于提升模型的可解释性与泛化性。我们将该算法命名为REACT（因果深度学习算法）。

为清晰阐述该算法，我们首先将因果概率图（CPG）定义为，其中元素代表变量对结局产生因果影响的概率，即。在训练过程中，我们交替学习预测模型与因果概率图矩阵，分别通过 预测阶段与因果发现阶段实现。REACT的具体实现细节将在A.7节中阐述。

预测阶段

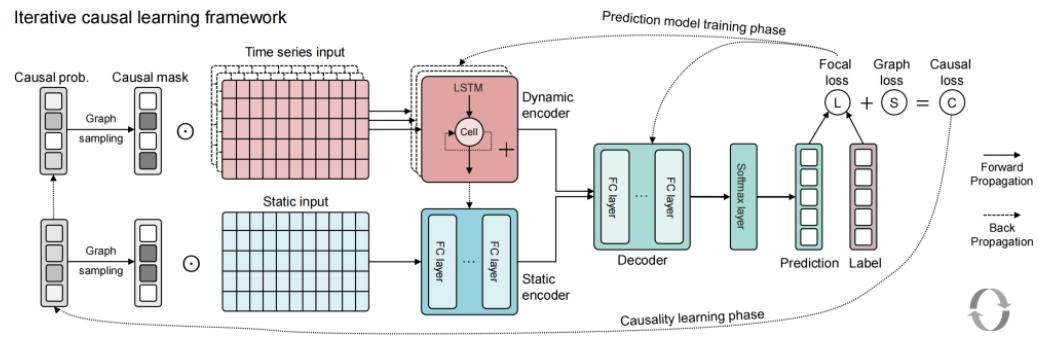
所提出的预测阶段旨在通过神经网络预测医疗结局，其网络结构如图2和补充方法图1所示。该神经网络的输入包括所有历史数据点（）以及已识别出的因果概率图（CPG）。

训练过程中，我们基于伯努利分布对因果图进行采样[9,33]，神经网络的输出为预测概率，公式如下：

其中，（代表伯努利分布）。在每个迷你批次（mini-batch）中，会为每个训练样本单独采样生成输入掩码。

本阶段中，输入掩码起到类似Dropout的正则化作用[34]，用于提升神经网络的稳健性。训练过程通过最小化焦点损失（Focal Loss）[35]函数 来更新网络参数，焦点损失函数公式如下：

式中，为迷你批次中的样本数量，为类别数量，为焦点损失函数中的系数，为指示函数（若，则；否则为0）。由于心脏手术相关急性肾损伤（CSA-AKI）的类别标签存在严重不平衡问题，焦点损失通过为难分样本和误分类样本分配更高权重，可有效解决这一问题。

softmax层输出的类别预测概率为。我们采用单一神经网络模型，同时预测不同时间窗口（6小时、12小时、24小时、48小时）内的AKI风险。具体而言，该模型会输出每个时间窗口内三类AKI（所有AKI、中重度AKI、重度AKI）的发生概率，最终共产生12个概率输出（4个时间窗口×3类AKI）。这种设计使模型既能利用数据中的共性模式，又能捕捉特定时间窗口的风险因素，相比为每个时间窗口单独训练模型更具效率，且通过单次推理即可实现全面的时间维度风险评估。

因果发现阶段

预测阶段结束后，进入因果发现阶段以学习因果概率图（CPG）。为确定因果概率，我们将其建模为，其中代表sigmoid函数（），为待学习的参数集合。

此外，由于输入数据在时间上始终先于结局，因此无需在因果概率图中学习边的方向。由于为离散变量，无法直接优化，我们采用Gumbel-Softmax技术[36]进行处理。通过最小化以下目标函数，对图参数进行优化：

式中，为前文定义的、用于惩罚预测误差的焦点损失，为 正则化项，用于实现所学习因果概率图的稀疏连接。若被惩罚至（此时），则可推断时序变量对结局不存在格兰杰因果影响。

我们在A.6节中进一步证明，在特定假设条件下，所识别出的因果向量会收敛到真实的格兰杰因果关系。在假设“无未观测混杂变量”与“时间先后性”的前提下，REACT能提取反映格兰杰因果效应的关联关系，并确定因果方向。具体而言，模型会评估每个变量对结局的预测能力，进而捕捉格兰杰因果效应；最终保留的变量为结局的直接因果因素，间接因果因素则被剔除（例如，若变量仅通过变量对结局产生影响，那么当被纳入模型后，会从因果因素中剔除）。

模拟干预

在预测阶段，输入掩码基于伯努利分布采样并起到正则化作用；而在因果发现阶段，该采样过程通过对每个变量实施模拟干预，模拟随机对照试验（RCT）。具体而言，我们通过随机纳入或排除某一变量对模型进行干预，并评估干预对结局产生的因果效应。

在每次训练迭代中，每个输入变量都会经历随机干预过程：以概率被剔除（），或以概率被保留（）。参数（通过计算得出）代表模型当前估计的变量对结局的因果影响程度。模型通过评估“变量存在时”与“变量被干预时”的预测性能差异，持续更新。

A.6节的研究表明，对于真正对结局有因果影响的变量，算法倾向于将其保留；反之，对于虚假关联变量，算法会逐步将其剔除：非因果变量的会收敛至0（频繁被干预但不影响预测结果），而具有重要因果意义的变量的会稳定在1附近（对这些变量的干预会显著影响预测结局）。这种掩码机制有效实现了系统性的因果干预，模拟了在训练过程中持续进行的“虚拟消融实验”，最终实现因果变量的识别。

参数的选择

因果阈值参数同样决定了模型纳入变量的数量。越小，模型会纳入更多对结局因果效应较弱的变量，可能捕捉到存在虚假关联的变量间动态关系，从而限制模型的迁移能力；反之，过大则可能损害模型的预测准确性。

我们通过优化内部验证准确性与模型复杂度之间的权衡关系来选择，外部验证结果仅作为独立验证依据。

模型的泛化性

REACT中采用的采样策略（）不仅能将因果概率图（CPG）融入神经网络，还能像Dropout[34]一样起到正则化作用，防止神经网络过拟合。因此，该模型从以下两方面提升性能与泛化性：

1. 因果发现阶段筛选出稳健的因果特征：补充图6的实证结果表明，仅使用6个因果变量时，模型的泛化性仍能提升；
2. 预测阶段防止神经网络过拟合：补充表5~8的实验结果显示，当仅使用因果特征训练另一个神经网络（未采用我们的因果深度学习策略）时，其性能仍低于REACT。这表明REACT不仅能通过识别因果变量提升泛化性，还能在训练过程中避免过拟合。

基于因果推断的重要性分析

利用已识别出的因果图，我们通过计算平均反事实概率来分析每个因果变量的重要性。由于所有动态变量在时间上均先于结局 ，因此图模型中不存在从指向的边。此外，若假设“无未观测混杂变量”，则通过对除外的其他变量进行条件控制，可阻断从到的所有后门路径，此时反事实概率可确定为：

式中，为变量的参考值，为剔除后的变量集合。我们重点分析反事实预测，并将个体重要性（IIM） 定义为：

个体重要性用于衡量某一变量对特定患者的重要程度。为计算所有患者的 平均重要性（AIM），公式如下：

式中，代表样本编号，代表总样本数。需注意的是，该重要性分析方法存在局限性：我们假设“无未观测混杂变量”，这一假设在实际场景中可能过于严格。若该假设不成立，因果推断分析可能存在偏差，计算结果将仅为深度学习模型的遮挡分析[37]。

A.7 实现细节

我们在搭载英特尔酷睿（Intel Core）中央处理器（CPU）和英伟达 geforce RTX 3090 图形处理器（GPU）的个人计算机（PC）上开展实验。我们使用 PyTorch1 框架实现本文提出的算法及基于神经网络的对比算法，使用 Python 库 xgboost2 实现极端梯度提升（XGBoost）算法。

网络架构

REACT 中的因果学习模型包含两个阶段，即结局预测阶段和因果发现阶段。其中，结局预测阶段采用基于长短期记忆网络（LSTM）和多层感知机（MLP）的神经网络。为同时处理静态输入和动态输入，该网络可进一步分为三部分：基于 MLP 的静态编码器、基于 LSTM 的动态编码器，以及另一个基于 MLP 的解码器。

对比模型

实验中提及的“LSTM/Transformer”（长短期记忆网络/转换器），指与 LSTM/Transformer 动态编码器结构相同的模型；“MLP”（多层感知机）指全 MLP 网络，即先将所有动态输入和静态输入展平（flatten），再输入单个 MLP 编码器。

“MLP”“LSTM”和“XGBoost”均未引入因果发现模块，即使用所有变量进行预测。如补充表 5~8 所示，在部分实验中，我们还测试了“仅使用筛选后变量训练常规神经网络（如 MLP、LSTM、Transformer）”的场景——该场景采用“深度学习前先进行特征筛选”的策略，而非本文提出的因果学习策略。在此设置下，我们仅将筛选后的变量作为输入，其余变量设为 0，以保证可使用相同隐藏层宽度的同一网络架构进行实验。

对于 XGBoost 模型，由于我们的数据集包含超过 100 万个样本，无法一次性加载到内存中，因此采用数据迭代器（data iterator）的方式实现该模型，每个迭代器包含 5 万个样本。

训练策略

结局预测阶段

初始学习率设置为相对较高的值，随后逐步下降至初始值的 10%（使用 PyTorch 中的 torch.optim.lr_scheduler.StepLR 调度器，学习率衰减的乘法因子设为 (0.1^{1/\text{tot_epoch}})，其中 tot_epoch 为总训练轮次）。焦点损失（Focal Loss）中的系数 γ 设为 2。

因果发现阶段

初始时，因果概率图中所有元素 (\sigma(\theta)) 均设为 0.5，即参数 θ 全为 0。本阶段的学习率设置与结局预测阶段不同，但同样会逐步下降至初始值的 10%。有关参数的详细设置请参见下文。

为避免 (|\sigma(\theta)|_1)（(\sigma(\theta)) 的 L1 范数）过大，我们先将其除以 θ 中的元素总数，再乘以正则化参数 λ。

参数搜索

超参数在深度学习模型的开发中起着关键作用。我们对每个深度学习模型（含本文提出的因果学习模型）均采用标准的网格搜索（parameter grid search）方法寻找最优超参数。通过选择在验证集上表现最佳的超参数组合，确定最终使用的超参数。

由于每次训练需耗时数小时甚至数天，网格搜索仅能覆盖少量超参数值。补充表 4 列出了各参数的搜索范围，其中最终使用的参数以粗体标注。

to be continued

相关课程推荐

相关课程推荐