今儿和大家聊聊聚类算法模型~
聚类算法的价值在于,它能在没有先验标签的情况下,把看似杂乱的数据自动分成有结构的群体,帮我们理解数据的内在规律。
很多时候业务问题并不是预测一个结果,而是先搞清楚有哪些类型,聚类正好解决了这个起点问题。
在工业界,它被大量用在用户分群、异常检测、设备状态识别等场景中,直接影响运营决策和成本控制。
可以说,聚类算法常常不是终点模型,但它决定了后续分析和建模能不能走在正确的路上。
今儿分享的聚类模型有:
K-means聚类
目标:将数据划分为个簇,使得同一簇内的样本彼此尽可能接近(欧式距离小)。
方法:交替进行分配和更新两步,直到质心稳定。
直观理解:每个簇用一个质心(均值点)来代表,点归属于距离最近的质心。
核心原理
设数据集为,选择簇数,每个簇对应一个质心,以及簇集合。
优化目标(最小化簇内平方误差,Within-Cluster Sum of Squares, WCSS):
常用初始化为-means++,可加快收敛并提升效果。
Python实现
下面的代码用合成数据生成5个簇,使用K-means聚类,并绘制不同簇的散点以及星形质心。
可直观看到就近分配到质心的原理。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
# 1) 生成合成数据(5个簇)
X, y_true = make_blobs(
n_samples=1000,
centers=5,
cluster_std=[0.60, 0.50, 0.55, 0.45, 0.50],
random_state=42
)
# 2) 运行K-means
k = 5
kmeans = KMeans(
n_clusters=k,
init='k-means++', # 更稳定的初始化
n_init=10,
max_iter=300,
random_state=0
)
labels = kmeans.fit_predict(X)
centers = kmeans.cluster_centers_
# 3) 可视化
plt.figure(figsize=(8, 6), dpi=120)
bright_colors = ['red', 'blue', 'lime', 'purple', 'orange']
for i, color in enumerate(bright_colors):
cluster_points = X[labels == i]
plt.scatter(cluster_points[:, 0], cluster_points[:, 1],
c=color, s=30, alpha=0.85, label=f'簇 {i}',
edgecolors='white', linewidths=0.4)
plt.scatter(centers[:, 0], centers[:, 1],
c='yellow', s=300, marker='*',
edgecolors='black', linewidths=1.2,
label='质心')
plt.title('K-means聚类(不同簇,星形为质心)', fontsize=14)
plt.xlabel('特征1')
plt.ylabel('特征2')
plt.legend(loc='best', frameon=True)
plt.grid(alpha=0.25, linestyle='--')
plt.tight_layout()
plt.show()
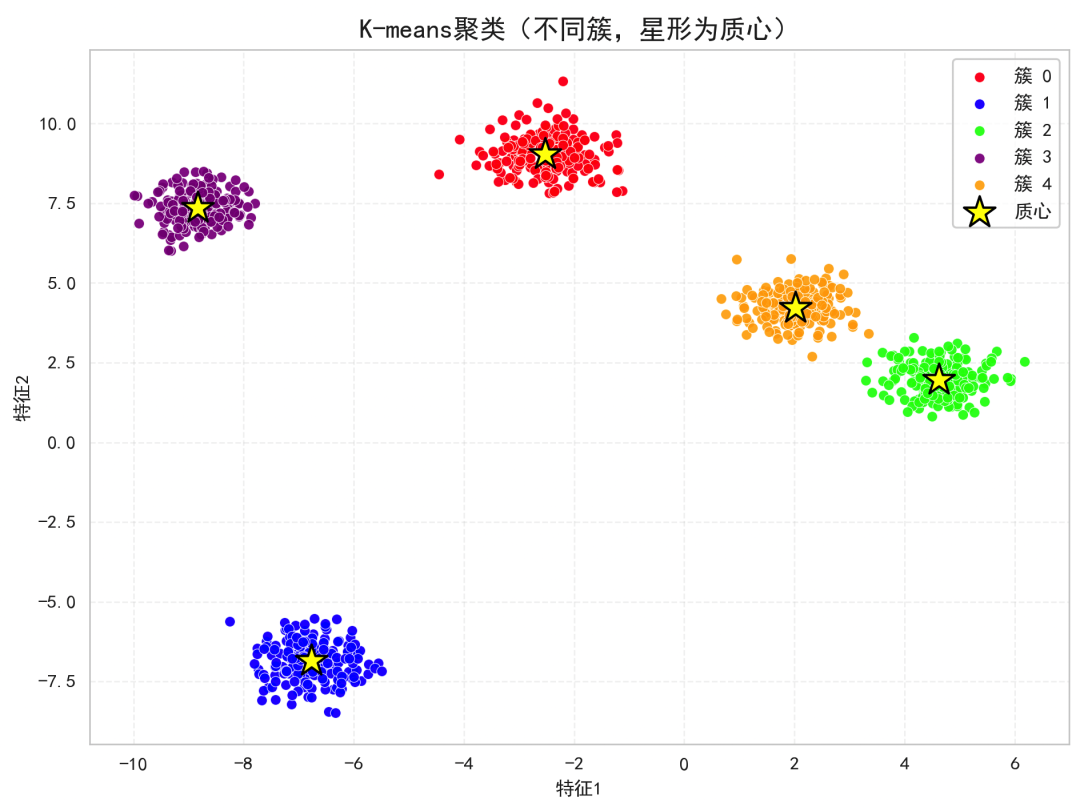
颜色代表簇分配(对应公式中的),星形点是质心。
算法通过反复分配到最近质心与用均值更新质心来减少总的簇内平方误差。
层次聚类
层次聚类是一类无监督学习方法,它不直接给出平坦的簇划分,而是通过逐步合并(或拆分)样本构建出一个树状的层次结构(树状图/谱系图,dendrogram)。
最常用的是自底向上的凝聚式层次聚类:开始时每个样本各自为簇,随后按簇间距离最小的原则迭代地合并成更大的簇,直到达到目标簇数或距离阈值。
核心优点:
- 不需要事先确定簇的形状(如高斯假设),可以通过切割树状图得到不同层级的聚类结果。
典型缺点:
- 朴素实现的时间复杂度较高(通常为),对大规模数据可能较慢。
- 一旦合并无法撤销(贪心策略),对噪声和度量选择较敏感。
核心原理
以凝聚式层次聚类为例,每一步选择使簇间距离最小的一对簇合并。
设样本点,欧氏距离为
给定两个簇,不同的连结定义如下:
- Ward 连结(方差最小化,最常用的默认选项之一): 设和分别为簇与的均值,Ward合并代价(聚合后总平方误差的增量)为
每一步选择使最小的一对簇进行合并。
迭代合并步骤:
将与合并为新簇,更新簇间距离,直到达到指定簇数或切割高度阈值。
Python实现
生成一个二维的合成数据集。
使用 sklearn 的 AgglomerativeClustering(Ward连结)得到3个簇。
使用 SciPy 画出对应的树状图(dendrogram),并在合适的高度画一条水平线表示切割得到3簇。在右侧画出聚类结果的散点图。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn.cluster import AgglomerativeClustering
from scipy.cluster.hierarchy import linkage, dendrogram
# 1) 生成合成数据(2D)
np.random.seed(42)
X, y_true = make_blobs(n_samples=75,
centers=[(-6, -2), (0, 8), (6, -4)],
cluster_std=[1.0, 1.1, 1.3],
random_state=42)
# 2) 凝聚式层次聚类(Ward)
n_clusters = 3
model = AgglomerativeClustering(n_clusters=n_clusters, linkage='ward')
y_pred = model.fit_predict(X)
# 3) 用SciPy计算linkage并画树状图
Z = linkage(X, method='ward') # 与sklearn的Ward一致(欧氏距离)
# 为了得到3簇的切割高度:在从3到2簇的合并高度稍下方画线
cut_height = Z[-(n_clusters - 1), 2] * 0.99
palette = ['#e41a1c', '#377eb8', '#4daf4a', '#984ea3', '#ff7f00']
plt.figure(figsize=(12, 5))
# 左:树状图
ax1 = plt.subplot(1, 2, 1)
dendrogram(Z,
color_threshold=cut_height,
above_threshold_color='#999999', # 阈值以上用灰色
leaf_rotation=90,
leaf_font_size=8)
plt.axhline(y=cut_height, color='#ff7f00', linestyle='--', linewidth=2, label='切割高度')
plt.title('层次聚类树状图(Ward)', fontsize=12)
plt.xlabel('样本索引'
, fontsize=10)
plt.ylabel('合并距离/代价', fontsize=10)
plt.legend()
# 右:聚类散点图
ax2 = plt.subplot(1, 2, 2)
for k in range(n_clusters):
mask = (y_pred == k)
plt.scatter(X[mask, 0], X[mask, 1],
s=70, c=palette[k], edgecolors='white', linewidths=0.8,
alpha=0.95, label=f'簇 {k}')
plt.title('AgglomerativeClustering(Ward)聚类结果', fontsize=12)
plt.xlabel('X1', fontsize=10)
plt.ylabel('X2', fontsize=10)
plt.legend()
plt.grid(alpha=0.3)
plt.tight_layout()
plt.show()
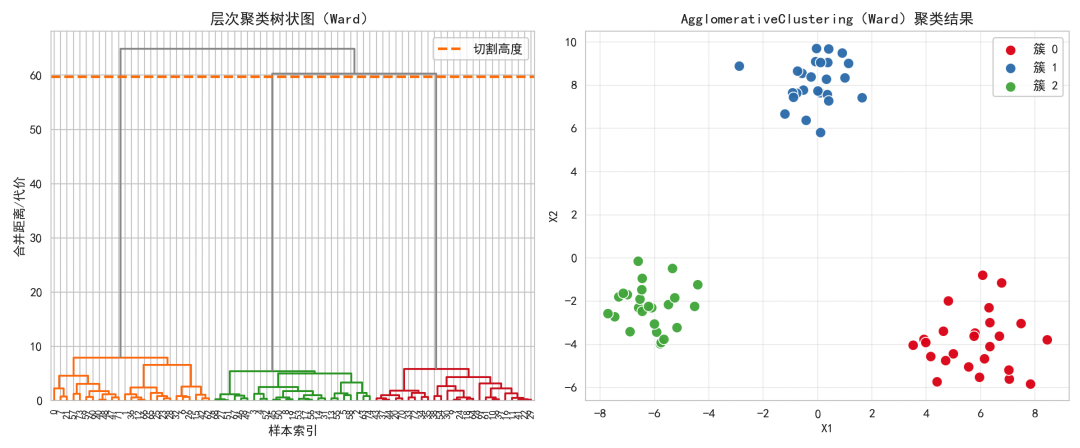
左图的树状图展示了从每个点作为簇开始,逐步合并直至全部合并的过程。横线(橙色虚线)所示的切割高度对应把树切开得到3个簇。
右图的散点图展示了最终的3个簇。Ward连结倾向于合并后簇的紧致性(最小化簇内平方和的增量),因此常得到较为球形、紧凑的簇划分。
高斯混合模型
高斯混合模型(Gaussian Mixture Model, GMM)是一种将数据分布表示为多个高斯分布加权求和的概率模型。
用于聚类时,GMM能刻画软聚类(每个样本属于各簇的概率)以及非球形(椭圆形)簇的结构,相比K-means更灵活。
核心思想
用个高斯分量来近似数据的总体分布;
每个分量有其权重、均值、协方差;
通过EM算法最大化观测数据的似然,学习参数。
模型形式:
其中,高斯密度为:
EM算法的关键步骤:
最大化的目标(对数似然):
Python实现
下面用二维数据集,拟合GMM并画出:
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Ellipse
from sklearn.mixture import GaussianMixture
from sklearn.preprocessing import StandardScaler
COLORS = ['#e41a1c', '#377eb8', '#4daf4a', '#984ea3', '#ff7f00']
np.random.seed(42)
# 1) 生成合成数据:3个椭圆形的高斯簇
mean1 = np.array([0, 0])
cov1 = np.array([[2.0, 1.2],
[1.2, 1.5]])
mean2 = np.array([6, 4])
cov2 = np.array([[1.5, -1.0],
[-1.0, 2.0]])
mean3 = np.array([-5, 5])
cov3 = np.array([[1.0, 0.0],
[0.0, 3.0]])
X1 = np.random.multivariate_normal(mean1, cov1, size=300)
X2 = np.random.multivariate_normal(mean2, cov2, size=250)
X3 = np.random.multivariate_normal(mean3, cov3, size=250)
X = np.vstack([X1, X2, X3])
# 可选:标准化(有助稳定拟合),但这里保持原始以便直观显示椭圆
# X = StandardScaler().fit_transform(X)
# 2) 拟合GMM
K = 3
gmm = GaussianMixture(n_components=K, covariance_type='full', random_state=42)
gmm.fit(X)
labels = gmm.predict(X) # 硬标签:argmax责任度
resp = gmm.predict_proba(X) # 责任度:软分配 (N x K)
means = gmm.means_ # (K x 2)
covs = gmm.covariances_ # (K x 2 x 2)
weights = gmm.weights_ # (K,)
# 3) 可视化:数据点 + 每个分量的协方差椭圆 + 混合密度等高线
def draw_ellipse(ax, mean, cov, color, n_std=2.0, lw=2.5):
# 根据协方差的特征分解绘制椭圆(n_std倍标准差)
vals, vecs = np.linalg.eigh(cov)
order = vals.argsort()[::-1]
vals, vecs = vals[order], vecs[:, order]
angle = np.degrees(np.arctan2(vecs[1, 0], vecs[0, 0]))
width, height = 2 * n_std * np.sqrt(vals) # 2*std 显示直径
ellip = Ellipse(xy=mean, width=width, height=height, angle=angle,
edgecolor=color, facecolor='none', lw=lw)
ax.add_patch(ellip)
# 网格评估密度
x_min, x_max = X[:,0].min()-3, X[:,0].max()+3
y_min, y_max = X[:,1].min()-3, X[:,1].max()+3
xx, yy = np.meshgrid(np.linspace(x_min, x_max, 300),
np.linspace(y_min, y_max, 300))
grid = np.column_stack([xx.ravel(), yy.ravel()])
logp = gmm.score_samples(grid) # log p(x)
p = np.exp(logp).reshape(xx.shape)
plt.figure(figsize=(9, 7))
# 混合密度等高线(柔和透明以不遮盖点)
contours = plt.contourf(xx, yy, p, levels=15, cmap='plasma', alpha=0.35)
# 数据点(按簇着色)
for k in range(K):
plt.scatter(X[labels==k, 0], X[labels==k, 1],
s=40, c=COLORS[k], edgecolors='black', linewidths=0.3,
label=f'Cluster {k+1}', alpha=0.95)
# 绘制每个分量的均值和协方差椭圆(2σ和3σ,体现椭圆簇形)
for k in range(K):
draw_ellipse(plt.gca(), means[k], covs[k], COLORS[k], n_std=2.0, lw=2.8)
draw_ellipse(plt.gca(), means[k], covs[k], COLORS[k], n_std=3.0, lw=1.8)
plt.scatter(means[k,0], means[k,1], marker=
'*', s=220,
c=COLORS[k], edgecolors='black', linewidths=0.5,
label=f'Mean {k+1}')
plt.title('GMM聚类:椭圆分量 + 混合密度等高线', fontsize=14)
plt.xlabel('x1'); plt.ylabel('x2')
plt.legend(loc='upper right', fontsize=10, frameon=True)
plt.tight_layout()
plt.show()
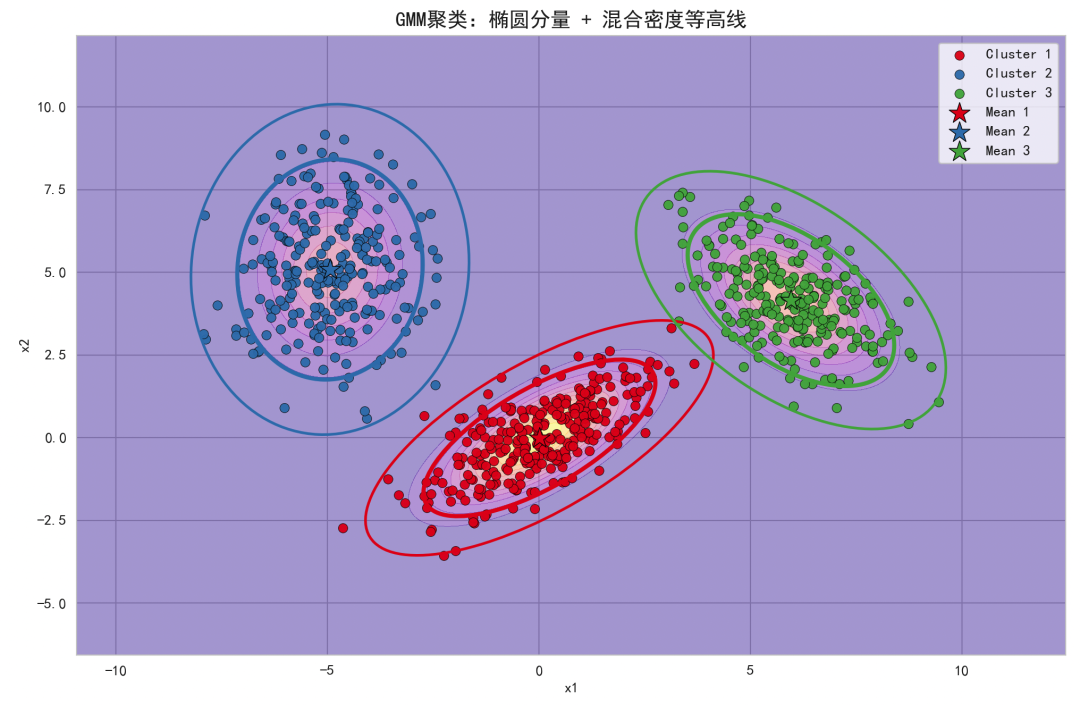
背景的plasma等高线展示了混合概率密度的形状(概率模型),椭圆展示每个高斯分量的协方差结构(非球形簇)。
点的颜色是硬聚类结果(由最大责任度得到),体现GMM将数据划分为多个高斯簇;若需要展示软聚类,可根据最大责任度调整点的透明度或使用连续颜色映射。
DBSCAN
DBSCAN(Density-Based Spatial Clustering of Applications with Noise)是一种基于密度的聚类算法。
通过邻域半径和最小点数两个参数来定义密度、识别核心点、边界点和噪声点,从而能发现任意形状的簇,并自动识别噪声(离群点),不需要预先设定簇的数量。
核心优势:
核心参数:
- :最小邻域点数(含自身),一般可取维度数的2–4倍或经验设定
核心原理
给定数据集 ,距离度量(常用欧氏距离):
-邻域:
核心点:若 ,则点 为核心点。
直接密度可达:若 且 是核心点,则 由 直接密度可达。
密度可达:若存在点序列 ,其中,且对所有(),由直接密度可达,则称对 密度可达。
密度相连:若存在某点 ,使得与均对密度可达,则称与 密度相连。
簇:数据集中最大密度相连的点集;不属于任何簇的点为噪声(Noise)。
直观理解,以半径 画邻域圆,如果圆里点数 ≥ MinPts,则该点是核心点。核心点能够
扩展形成簇;邻域内不足但连接到核心点的为边界点;落在稀疏区域的为噪声。
Python实现
我们使用合成数据(两个月牙形簇 + 少量随机离群点),运行DBSCAN并用颜色标出簇、核心点、边界点和噪声,同时用绿色圆环示意邻域,给大家体现算法原理。
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import DBSCAN
from sklearn.datasets import make_moons
# 1) 构造合成数据:月牙形 + 离群点
rng = np.random.default_rng(42)
X_moons, _ = make_moons(n_samples=1000, noise=0.06, random_state=42)
# 随机离群点(均匀采样以制造噪声)
outliers = rng.uniform(low=[-2.0, -1.2], high=[3.0, 2.2], size=(80, 2))
X = np.vstack([X_moons, outliers])
# 2) 运行DBSCAN
eps = 0.25 # 邻域半径(可微调)
min_pts = 6 # 最小邻域点数(含自身)
db = DBSCAN(eps=eps, min_samples=min_pts)
labels = db.fit_predict(X)
# 核心点索引
core_indices = getattr(db, "core_sample_indices_", [])
core_mask = np.zeros(len(X), dtype=bool)
core_mask[core_indices] = True
# 边界点与噪声掩码
noise_mask = labels == -1
border_mask = (labels != -1) & (~core_mask)
palette = [
"red", "blue", "orange", "green", "magenta",
"cyan", "gold", "purple", "fuchsia", "lime"
]
unique_labels = sorted(set(labels) - {-1})
# 3) 绘图
plt.figure(figsize=(
7.5, 6.5), facecolor="white")
ax = plt.gca()
# 画簇中的核心点和边界点
for i, lab in enumerate(unique_labels):
col = palette[i % len(palette)]
# 核心点(加粗、亮色)
ax.scatter(X[(labels == lab) & core_mask, 0],
X[(labels == lab) & core_mask, 1],
s=80, c=col, marker="o",
edgecolors="white", linewidths=0.9,
alpha=0.95, label=f"Cluster {lab} (core)")
# 边界点(同色、稍小)
ax.scatter(X[(labels == lab) & border_mask, 0],
X[(labels == lab) & border_mask, 1],
s=50, c=col, marker="o",
edgecolors="black", linewidths=0.6,
alpha=0.9, label=f"Cluster {lab} (border)")
# 噪声点(黑色叉)
ax.scatter(X[noise_mask, 0], X[noise_mask, 1],
s=60, c="black", marker="x",
alpha=0.85, label="Noise")
# 用绿色圆环示意几个核心点的 ε-邻域
core_points = X[core_mask]
if len(core_points) > 0:
sel = rng.choice(len(core_points), size=min(2, len(core_points)), replace=False)
for p in core_points[sel]:
circle = plt.Circle((p[0], p[1]), eps, color="lime",
fill=False, lw=2.0, alpha=0.8)
ax.add_patch(circle)
ax.plot([p[0]], [p[1]], marker='o', markersize=9,
markerfacecolor='none', markeredgecolor='lime', markeredgewidth=2.0)
ax.set_title(f"DBSCAN clustering (eps={eps}, MinPts={min_pts})", fontsize=13)
ax.set_xlabel("x1")
ax.set_ylabel("x2")
ax.set_aspect("equal", adjustable="box")
ax.grid(True, alpha=0.25, linestyle="--"
)
ax.legend(loc="upper right", fontsize=9, framealpha=0.9)
plt.tight_layout()
plt.show()
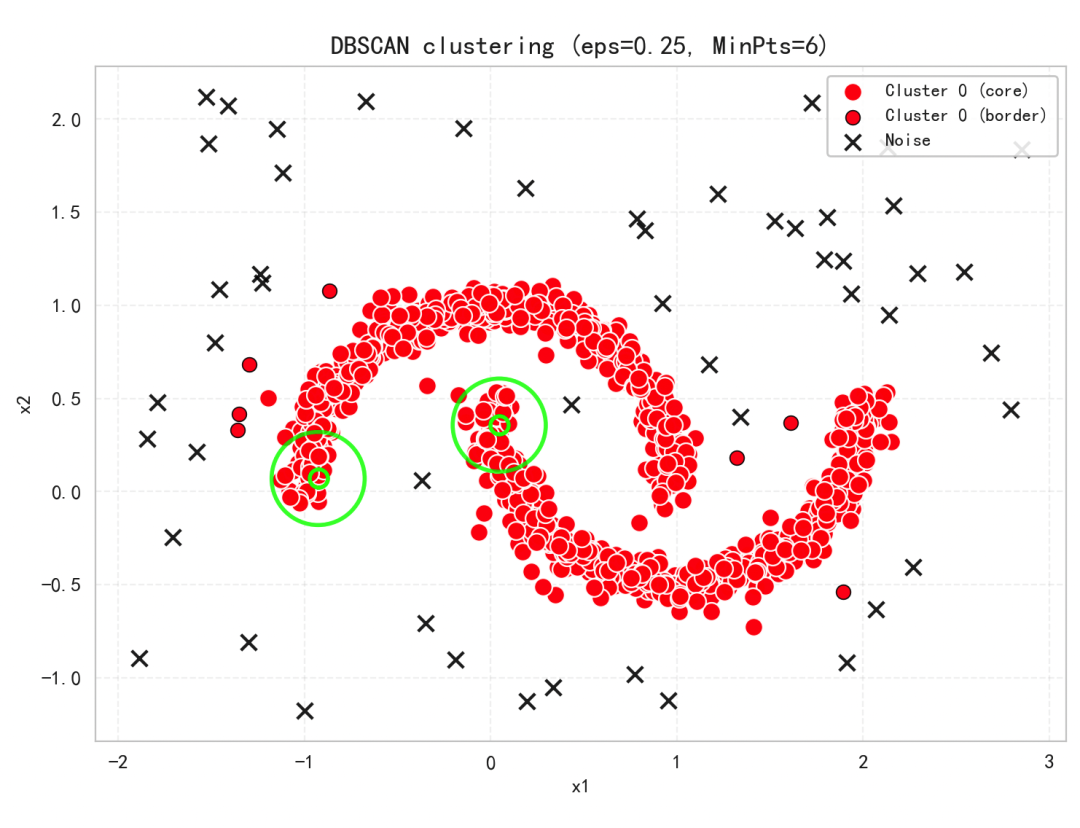
若簇被误分或噪声过多,可适当增大/减小 与 。常用经验是用k-距离图(例如取 )寻找距离拐点,以设定合适的 。
模糊C均值
模糊C均值是一种软聚类方法:与K-Means那样把每个样本硬性分到某一个簇不同,FCM为每个样本分配对每个簇的隶属度,介于0到1之间,并且每个样本的所有隶属度之和为1。
这让FCM在簇边界或重叠区域能更自然地表达不确定性和模糊性。
核心思想是最小化加权的簇内平方误差,其中权重由隶属度的模糊因子控制(常用)。
目标函数:
约束条件:
更新规则(交替迭代直至收敛):
当增大时,隶属度更平滑更平均;当时更接近硬聚类。
算法流程简述:
- 重复:更新隶属度 → 更新簇中心 → 直至中心/目标函数收敛或达到迭代上限
Python实现
我们用PyTorch实现FCM的核心更新公式,生成三团有重叠的二维数据;
用隶属度加权的颜色混合可视化:每个点的颜色为三个簇基本色(红/绿/蓝)的加权混合,混色越明显说明该点在多个簇都有较高隶属度,体现模糊特性;
绘制黑色X标出最终簇中心。
import torch
import numpy as np
import matplotlib.pyplot as plt
def fuzzy_c_means(X, n_clusters=3, m=2.0, max_iter=100, tol=1e-4, seed=0):
"""
Fuzzy C-Means using PyTorch.
X: torch.Tensor of shape (N, D)
Returns:
C: torch.Tensor of shape (c, D) - cluster centers
U: torch.Tensor of shape (N, c) - membership matrix
"""
torch.manual_seed(seed)
N, D = X.shape
# 初始化中心:随机选择数据点
idx = torch.randperm(N)[:n_clusters]
C = X[idx].clone() # (c, D)
eps = 1e-12
# 迭代
for it in range(max_iter):
C_prev = C.clone()
# 距离矩阵 d(i,k) = ||x_i - c_k||
d = torch.cdist(X, C, p=2) + eps # (N, c)
# 更新隶属度 U
# u_ik = 1 / sum_j (d_ik / d_ij)^(2/(m-1))
exponent = 2.0 / (m - 1.0)
ratio = (d[:, :, None] / d[:, None, :]) ** exponent # (N, c, c)
denom = ratio.sum(dim=2) # (N, c)
U = 1.0 / denom # (N, c)
# 更新簇中心 C
w = U ** m # (N, c)
denom_c = w.sum(dim=0) # (c,)
num_c = X.T @ w # (D, c)
C = (num_c / (denom_c + eps)).T # (c, D)
# 检查收敛(中心变化)
shift = torch.norm(C - C_prev)
if shift.item() < tol:
# print(f"Converged at iter {it}, shift={shift.item():.6f}")
break
return C, U
# 生成合成数据(3个高斯簇,带重叠)
def make_data(seed=0, n_per=150):
torch.manual_seed(seed)
centers = torch.tensor([[0.0, 0.0],
[5.0, 5.0],
[-5.0, 5.0]])
Xs = []
for c in centers:
Xs.append(c + 1.6 * torch.randn(n_per, 2))
X = torch.cat(Xs, dim=0)
return X
if __name__ ==
"__main__":
# 数据
X = make_data(seed=42, n_per=150) # 共450点
# 运行FCM
C, U = fuzzy_c_means(X, n_clusters=3, m=2.0, max_iter=200, tol=1e-5, seed=42)
# 将隶属度映射为RGB颜色
# 每个簇的基础色:R, G, B
base_colors = np.array([
[1.0, 0.05, 0.05], # bright red
[0.05, 0.95, 0.05], # bright green
[0.1, 0.1, 1.0] # bright blue
], dtype=np.float32)
U_np = U.detach().cpu().numpy() # (N, c)
point_colors = U_np @ base_colors # (N, 3), 隶属度线性混色
# 绘图
plt.figure(figsize=(8, 6), dpi=140)
plt.scatter(X[:, 0].numpy(), X[:, 1].numpy(),
c=point_colors, s=28, alpha=0.95, edgecolors='none', label='数据点(颜色=隶属度混色)')
# 中心
plt.scatter(C[:, 0].numpy(), C[:, 1].numpy(),
marker='X', s=220, c='black', edgecolors='white', linewidths=2.0, label='聚类中心')
plt.title("模糊C均值 (FCM):隶属度混色可视化", fontsize=14)
plt.xlabel("X1", fontsize=12)
plt.ylabel("X2", fontsize=12)
plt.legend(loc='best', fontsize=10)
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()
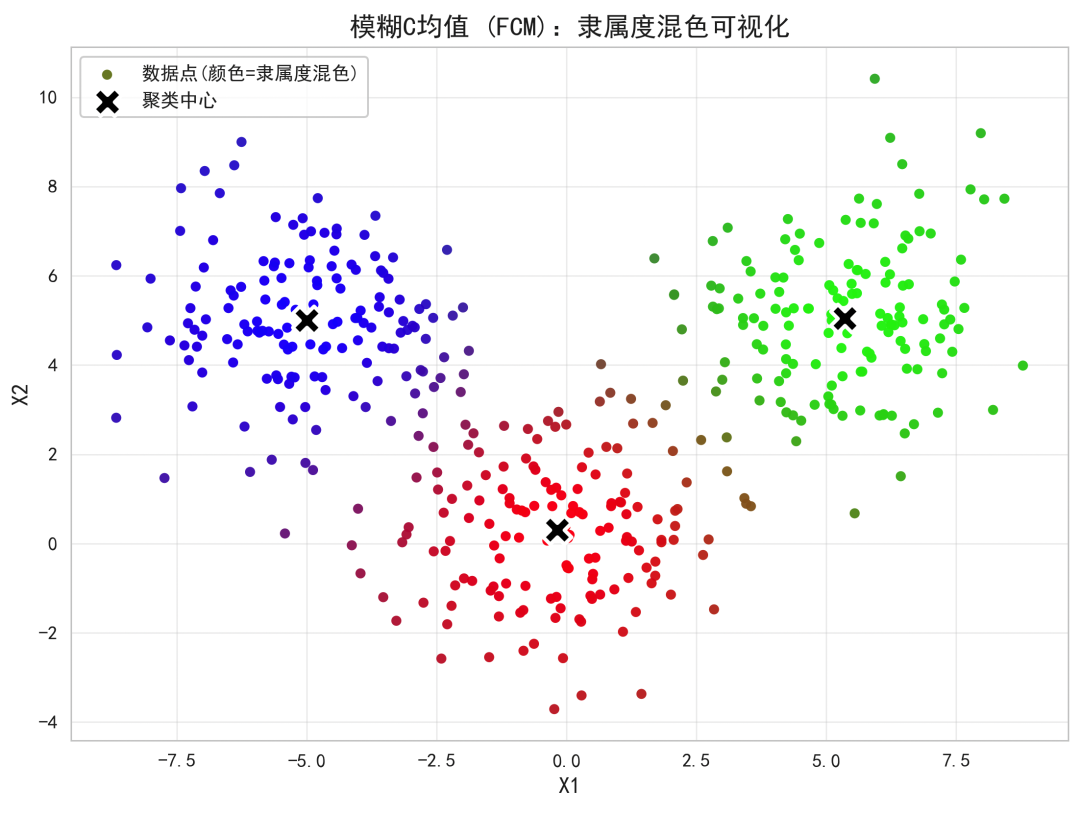
- 每个点的颜色是三个簇基本色的加权混合,权重正是该点对三个簇的隶属度;
- 在簇重叠区域,点会呈现明显的混色(如紫色、青色、黄绿色等),体现模糊归属;
最后
大家可以自行执行上述代码,都是完整的,整体理解聚类算法的核心含义,以及不同聚类算法个侧重点~