
随着材料基因组计划的发展,高通量制备和分析材料成为必然。面对大规模的测量数据,我们如果逐个对其进行分析并从中找到感兴趣的样本数据,无疑会消耗大量的时间和精力。机器学习作为大数据处理中常使用的技术,有助于我们提高分析效率,发现隐含在数据中的规律。
接下来,我们通过一个具体的例子介绍如何借助机器学习方法分析高通量XRD数据。C. J. Long等人通过在单个硅片上沉积三元Fe-Ga-Pd化合物薄膜,得到535个三元Fe-Ga-Pd成分连续变化的1.75*1.75mm2大小的样品[1]。经过XRD表征,得到其中273个样品的衍射数据。之后,对衍射数据进行扣除背底等处理。如何提高分析这些XRD数据效率呢?我们可以借助机器学习中的聚类算法,对273个XRD样品数据进行聚类,将尽可能的单相样本归并到同一个聚类簇,这样我们只要分析各个聚类簇中代表性的样品数据就可以大大提高分析效率。
在进行聚类之前,我们需要设计可以度量样品数据间相似性的参量,然后在其基础上进行聚类。在这里,我们采用相关系数来衡量样品数据间的相似性。两个样品衍射数据x,y的相关系数为:
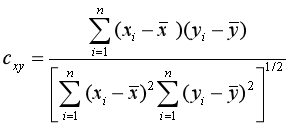
其中,n表示单条衍射谱中的数据点数目。相关系数的取值范围为[-1,1],1表示两个样品的衍射谱是完全相关的,0表示完全不相关,-1表示完全反相关。基于相关系数,我们可以进一步定义距离dxy =(1-cxy)/2,dxy的取值范围为[0, 1],值越小表示两个样品衍射谱越相似。由于我们有N个样品的衍射数据,这样我们就可以得到一个N×N的距离矩阵D。这个距离矩阵D表示了各个样品衍射数据间的相似性。由于距离矩阵中的dij不是按照欧氏距离定义的,所以在三维空间中按照距离矩阵展示N个点是难以实现的。但是,我们可以通过主成分分析,保留主要特征,将上述矩阵约化到三维空间中,如图1所示。
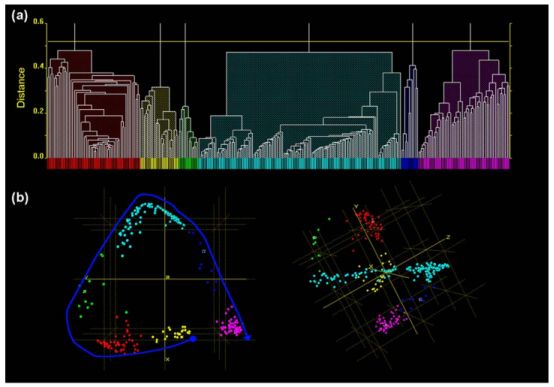
图1 (a)层级聚类算法,X轴上每一条竖线对应一个样本点,不同聚类簇用不同颜色标注。(b)聚类后的样本在三维空间中的分布,左图中蓝线为层级聚类算法使用的路径。
基于约化后的距离矩阵,我们对这些样本采用无监督学习中的层级聚类算法进行聚类。该算法先将数据集中每个样本看做一个初始聚类簇,然后在算法运行的每一步中找出距离最近的两个聚类簇进行合并,该过程不断重复直至达到预设的聚类簇个数。如图1(a)所示,图中的X轴表示沿着图1(b)中的蓝线路径对应各个样本点依次排列,y轴表示合并聚类时对应的间距。图1(b)为聚类后各个样本点在三维空间中的分布图,不同颜色对应不同的聚类簇。
从图中可以看出,样本分为六个聚类簇,其中有的聚类簇分布比较集中,比如红色聚类簇和紫红色聚类簇,有的聚类簇则分布比较离散,如绿色聚类簇和蓝色聚类簇。分布比较集中的聚类簇可能对应单相,分布比较离散的聚类簇可能对应两相混合或者单个相中某个峰有连续迁移。
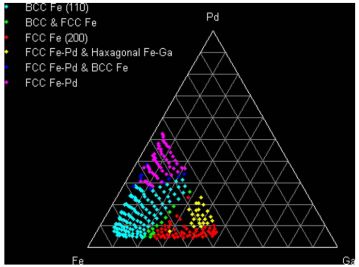
图2 三元相图,其中不同颜色样本点对应图1中相应的聚类簇
我们将聚类结果对应到三元相图中,并将各个聚类簇XRD和晶体学数据库中的结构进行对照,找出其中代表性的结构。如图2所示,紫红色为FCC Fe-Pd,蓝色为FCC Fe-Pd和BCC Fe,青色为BCC Fe,绿色为BCC Fe和FCC Fe,红色为FCC Fe,黄色为FCC Fe-Pd和六方Fe-Ga。蓝色和绿色样本分别分布在两个单相间,对应两个单相的混合。
以上结果证明,通过利用机器学习中的降维和聚类算法有助于高效分析高通量XRD数据,识别其中的相分布及不同相的交界处,帮助我们快速找到感兴趣样品区域。
参考文献:
[1] Long C J, Hattrick-Simpers J, Murakami M, et al. Rapid structural mapping of ternary metallic alloy systems using the combinatorial approach and cluster analysis[J]. Review of Scientific Instruments, 2007, 78(7): 072217.
对机器学习应用于材料科学感兴趣?材料人8月底举办的线下材料计算培训涉及机器学习,欢迎参加。如有需要,请咨询微信maxw89。
投稿邮箱
tougao@cailiaoren.com
投稿以及内容合作可加微信
cailiaorenvip
材料人重磅推出特色计算服务,为广大材料&化学科技工作者提供包括第一性原理计算、有限元计算、分子动力学计算、流体力学计算、相图计算等一系列材料计算代算服务,以及相关的计算指导、培训服务。如有需要,欢迎扫码添加客服咨询(微信号:cailiaoren001)

