作者:华校专
作者信息:
华校专,曾任阿里巴巴资深算法工程师、智易科技首席算法研究员,现任腾讯高级研究员,《Python 大战机器学习》的作者。
编者按:
算法工程师必备系列更新啦!继上次推出了算法工程师必备的特征工程后,小编继续整理了必要的机器学习知识,全部以干货的内容呈现,哪里不会学哪里,老板再也不用担心你的基础问题!接下来,就让我们紧跟作者的步伐,一起畅游聚类世界吧!
聚类(下)
三、密度聚类
- 密度聚类
density-based clustering假设聚类结构能够通过样本分布的紧密程度确定。 - 密度聚类算法从样本的密度的角度来考察样本之间的可连接性,并基于可连接样本的不断扩张聚类簇,从而获得最终的聚类结果。
3.1 DBSCAN 算法
DBSCAN是一种著名的密度聚类算法,它基于一组邻域参数 来刻画样本分布的紧密程度。
给定数据集 , 定义:
即: 包含了样本集 中与 距离不大于 的所有的样本。
即:若 的 -邻域中至少包含 个样本,则 是一个核心对象。
密度直达directyl density-reachable:若 是一个核心对象,且 , 则称 由 密度直达,记作 。
密度相连density-connected:对于 和 ,若存在 ,使得 与 均由 密度可达,则称 与 密度相连,记作。
- 核心对象
core object:若
,则称 是一个核心对象。
DBSCAN算法的簇定义:给定邻域参数 , 一个簇 是满足下列性质的非空样本子集:
即一个簇是由密度可达关系导出的最大的密度相连样本集合。
DBSCAN算法的思想:若 为核心对象,则 密度可达的所有样本组成的集合记作 。可以证明 就是满足连接性与最大性的簇。
于是 DBSCAN 算法首先任选数据集中的一个核心对象作为种子seed,再由此出发确定相应的聚类簇。
算法步骤:
(1) 初始化核心对象集合为空集:
(2) 寻找核心对象:
(2.1) 遍历所有的样本点 , 计算
(2.2) 如果 ,则
(3) 迭代:以任一未访问过的核心对象为出发点,找出有其密度可达的样本生成的聚类簇,直到所有核心对象都被访问为止。
- 若在核心对象 的寻找密度可达的样本的过程中,发现核心对象 是由 密度可达的,且 尚未被访问,则将 加入 所属的簇,并且标记 为已访问。
- 对于 中的样本点,它只可能属于某一个聚类簇。因此在核心对象 的寻找密度可达的样本的过程中,它只能在标记为未访问的样本中寻找 标记为已访问的样本已经属于某个聚类簇了)。
- 若样本集的密度不均匀,聚类间距差相差很大时,聚类质量较差。因为此时参数 和 MinPts 的选择比较困难。
3.2 Mean-Shift 算法
Mean-Shift 是基于核密度估计的爬山算法,可以用于聚类、图像分割、跟踪等领域。
Mean-Shift 算法的基本思路是:
移动过程中,兴趣域范围内的所有样本都标记为同一个簇。
因此Mean-Shift 会向着密度最大的区域移动。
下图中:蓝色为当前的兴趣域,红色为当前的中心点 紫色向量为mean shift 向量,灰色为移动之后的兴趣域 。
- 如果
mean shift 向量为 ,则停止移动,说明兴趣域 已到达数据点最密集的区域。 然后计算当前的mean shift 向量,兴趣域的中心移动为: 。

在计算mean shift 向量的过程中假设每个样本的作用都是相等的。实际上随着样本与中心点的距离不同,样本对于mean shift 向量的贡献不同。
定义高斯核函数为: ,则重新mean shift 向量定义为:
其中 称做带宽。 刻画了样本 距离中心点 相对于半径 的相对距离。
Mean_Shift 算法:
迭代,直到所有的样本都被访问过。迭代过程为(设已有的簇为 1,2,\cdots,L-1 ):
(1) 在未访问过的样本中随机选择一个点作为中心点 ,找出距它半径为 的兴趣域,记做 。将 中的样本的簇标记设置为 (一个新的簇)。
(2) 计算当前的mean shift 向量,兴趣域中心的移动为:
在移动过程中,兴趣域内的所有点标记为访问过,并且将它们的簇标记设置为 。
(3) 如果 ,则本次结束本次迭代。
(4) 设已有簇中,簇 的中心点 与 距离最近,如果 ,则将当前簇和簇合并。
合并时,当前簇中的样本的簇标记重新修改为 。
当所有的样本都被访问过时,重新分配样本的簇标记(因为可能有的样本被多个簇标记过):若样本被多个簇标记过,则选择最大的那个簇作为该样本的簇标记。即:尽可能保留大的簇。
输入:
(1) 数据集
(2) 带宽参数
(3) 迭代阈值 ,簇阈值
- 通常 采用放射状对称核函数 , 为 的轮廓函数, (一个正数)为标准化常数从而保证 的积分为 。
- 没有局部极小值点,因此当给定带宽参数
时,其聚类结果就是唯一的。
- 无法区分有意义的簇和无意义的簇。如:在
Mean_Shift 算法中,异常点也会形成它们自己的簇。
四、层次聚类
- 层次聚类
hierarchical clustering 试图在不同层次上对数据集进行划分,从而形成树形的聚类结构。
4.1 AGNES 算法
AGglomerative NESting:AGNES是一种常用的采用自底向上聚合策略的层次聚类算法。
AGNES首先将数据集中的每个样本看作一个初始的聚类簇,然后在算法运行的每一步中,找出距离最近的两个聚类簇进行合并。
合并过程不断重复,直到达到预设的聚类簇的个数。
这里的关键在于:如何计算聚类簇之间的距离?
由于每个簇就是一个集合,因此只需要采用关于集合的某个距离即可。给定聚类簇 , 有三种距离:
最小距离由两个簇的最近样本决定。
最大距离由两个簇的最远样本决定。
平均距离由两个簇的所有样本决定。
- 当
AGNES算法的聚类簇距离采用 时,称作单链接single-linkage算法。 - 当
AGNES算法的聚类簇距离采用 时,称作全链接complete-linkage算法。 - 当
AGNES算法的聚类簇距离采用 时,称作均链接average-linkage算法 。
输入:
(1) 数据集
(2) 聚类簇距离度量函数
(3) 聚类簇数量
算法步骤:
(1) 初始化:将每个样本都作为一个簇
(2) 迭代,终止条件为聚类簇的数量为 。迭代过程为:
计算聚类簇之间的距离,找出距离最近的两个簇,将这两个簇合并。
每进行一次迭代,聚类簇的数量就减少一些。
4.2 BIRCH 算法
BIRCH:Balanced Iterative Reducing and Clustering Using Hierarchies 算法通过聚类特征树CF Tree:Clustering Feature True来执行层次聚类,适合于样本量较大、聚类类别数较大的场景。
4.2.1 聚类特征
聚类特征CF:每个CF 都是刻画一个簇的特征的三元组: 。其中:
- :表示簇内样本的线性求和: ,其中 为该
CF 对应的簇。
根据CF 的定义可知:如果CF1 和 CF2 分别表示两个不相交的簇的特征,如果将这两个簇合并成一个大簇,则大簇的特征为: 。
即:CF 满足可加性。
簇心欧氏距离centroid Euclidian distance:,其中 分别为各自的簇心。
簇心曼哈顿距离centroid Manhattan distance: 。
簇连通平均距离average inter-cluster distance:
全连通平均距离average intra-cluster distance:
方差恶化距离variance incress distance: 。
4.2.2 CF 树
CF树的结构类似于平衡B+树 。树由三种结点构成:根结点、中间结点、叶结点。
根结点、中间结点:由若干个聚类特征CF ,以及这些CF 指向子结点的指针组成。
叶结点:由若干个聚类特征CF 组成。
(1) 叶结点没有子结点,因此CF 没有指向子结点的指针。
(2) 所有的叶结点通过双向链表连接起来。
(3) 在BIRCH 算法结束时,叶结点的每个CF 对应的样本集就对应了一个簇。

- 枝平衡因子 :非叶结点中,最多不能包含超过
个
CF 。 - 叶平衡因子 :叶结点中,最多不能包含超过 个
CF 。 - 空间阈值 :叶结点中,每个
CF 对应的子簇的大小(通过簇半径 来描述)不能超过 。
由于 CF 的可加性,所以 CF 树中,每个父结点的 CF 等于它所有子结点的所有 CF 之和。
输入:
(1) 样本集 ,
(2) 枝平衡因子
(2.1) 叶平衡因子
(2.2) 空间阈值
算法步骤:
(1) 初始化:CF 树的根结点为空。
(2) 随机从样本集
中选出一个样本,放入一个新的 CF 中,并将该 CF 放入到根结点中。
(3) 遍历 中的样本,并向 CF 树中插入。迭代停止条件为:样本集 中所有样本都插入到 CF 树中。
迭代过程如下:
(3.1) 随机从样本集 中选出一个样本 ,从根结点向下寻找与距离最近的叶结点,和里与最近的。
(3.2) 如果 加入到 对应的簇中之后,该簇的簇半径 ,则将
加入到 对应的簇中,并更新路径上的所有CF 。本次插入结束。
(3.3) 否则,创建一个新的CF,将 放入该CF 中,并将该CF 添加到叶结点 中。如果 的CF 数量小于 ,则更新路径上的所有CF 。本次插入结束。
(3.4) 否则,将叶结点 分裂为两个新的叶结点 。分裂方式为:
(3.4.1) 选择叶结点 中距离最远的两个CF,分别作为 中的首个CF 。
(3.4.2) 将叶结点 中剩下的CF 按照距离这两个CF 的远近,分别放置到 中。
(3.5) 依次向上检查父结点是否也需要分裂。如果需要,则按照和叶子结点分裂方式相同。
4.2.3 BIRCH 算法
BIRCH 算法的主要步骤是建立 CF 树,除此之外还涉及到 CF 树的瘦身、离群点的处理。
- 将数据点插入到
CF
树的过程中,用于存储CF 树结点及其相关信息的内存有限,导致部分数据点生长形成的CF 树占满了内存。因此需要对CF 树瘦身,从而使得剩下的数据点也能插入到CF 树中。 CF 树生长完毕后,如果叶结点中的CF 对应的簇太小,则会影响后续聚类的速度和质量。
BIRCH 瘦身是在将 增加的过程。算法会在内存中同时存放旧树 和新树 ,初始时刻 为空。
- 在完成所有的
CF 迁移之后, 为空, 就是瘦身后的 CF 树。
BIRCH 离群点的处理:
稀疏子簇:簇内数据点的数量远远少于所有子簇的平均数据点的那些子簇。
将稀疏子簇放入待定区时,需要同步更新CF 树上相关路径及结点。
如果数据点无法插入到CF 树中,则可以确定为真正的离群点。
- 当 中所有数据点都被插入之后,扫描待定区中的所有数据点(这些数据点就是候选的离群点),并尝试将其插入到
CF 树中。 - 在对
CF 瘦身之后,搜索所有叶结点中的所有子簇,寻找那些稀疏子簇,并将稀疏子簇放入待定区。
输入:
(1) 样本集
(2) 枝平衡因子
(2.1) 叶平衡因子
(2.2) 空间阈值
算法步骤:
(1) 建立 树。
(2) (可选)对CF 树瘦身、去除离群点,以及合并距离非常近的CF 。
(3) (可选)利用其它的一些聚类算法(如:k-means)对CF树的所有叶结点中的CF 进行聚类,得到新的CF 树。
这是为了消除由于样本读入顺序不同导致产生不合理的树结构。
这一步是对 结构进行聚类。由于每个CF 对应一组样本,因此对CF 聚类就是对 进行聚类。
(4) (可选)将上一步得到的、新的CF 树的叶结点中每个簇的中心点作为簇心,对所有样本按照它距这些中心点的距离远近进行聚类。
这是对上一步的结果进行精修。
- 节省内存。所有样本都存放在磁盘上,内存中仅仅存放
CF 结构。 -
结果依赖于数据点的插入顺序。原本属于同一个簇的两个点可能由于插入顺序相差很远,从而导致分配到不同的簇中。甚至同一个点在不同时刻插入,也会被分配到不同的簇中。
对非球状的簇聚类效果不好。这是因为簇直径 和簇间距离的计算方法导致。
每个结点只能包含规定数目的子结点,最后聚类的簇可能和真实的簇差距很大。
- 如果指定
,则需要将叶结点按照距离远近进行合并,直到叶结点中
CF 数量等于 。
五、谱聚类
谱聚类spectral clustering 是一种基于图论的聚类方法。
谱聚类的主要思想是:基于数据集 来构建图 ,其中:
通过对图 进行切割,之间的边的权重尽可能的低、各子图内的边的权重尽 可能的高。这样就完成了聚类。

5.1 邻接矩阵
在图 中,定义权重 为顶点 和 之间的权重,其中 。
定义 为邻接矩阵:

由于 为无向图,因此 。即: 。
定义度矩阵 为一个对角矩阵,其中对角线分别为各顶点的度:

-
对于顶点集合 的一个子集 ,定义为子集中点的个数;定义,为子集 中所有点的度之和。
2. 事实上在谱聚类中,通常只给定数据集 ,因此需要计算 出邻接矩阵。
基本思想是:距离较近的一对点(即相似都较高),边的权重较高;距离较远的一对点(即相似度较低),边的权重较低。
基本方法是:首先构建相似度矩阵 ,然后使用近邻法、K 近邻法、或者全连接法。

3. ϵ-近邻法:设置一个距离阈值 ,定义邻接矩阵为:
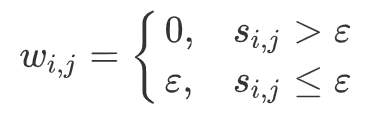
即:一对相似度小于 的点,边的权重为 否则边的权重为。
ϵ-近邻法得到的权重要么是 ,要么是 ,权重度量很不精确,因此实际应 用较少。
4. K 近邻法:利用 KNN 算法选择每个样本最近的 个点作为近邻,其它点与 当前点之间的边的权重为 。
这种做法会导致邻接矩阵 非对称,因为当 是 的 近邻时, 不 一定是 的 K 近邻。
为了解决对称性问题,有两种做法:
5. 全连接法:所有点之间的权重都大于
。
5.2 拉普拉斯矩阵
定义拉普拉斯矩阵 ,其中 为度矩阵、 为邻接矩阵。
拉普拉斯矩阵 的性质:
设其 个实特征值从小到大为 ,即: 。
是半正定的,且对应的 个特征值都大于等于0,且最小的特征值为 。
5.3 谱聚类算法
5.3.1 最小切图
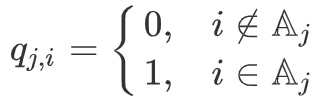
则有:
2. 最小切图算法: 最小的切分。即求解:
 3. 最小切图切分使得不同子图之间的边的权重尽可能的低,但是容易产生分割 出只包含几个顶点的较小子图的歪斜分割现象。
3. 最小切图切分使得不同子图之间的边的权重尽可能的低,但是容易产生分割 出只包含几个顶点的较小子图的歪斜分割现象。5.3.2 RatioCut 算法
RatioCut 切图不仅考虑最小化 ,它还考虑最大化每个子图的点的个数。即:
则有: