
马尔科夫态模型(Markov state model, MSM)是基于分子动力学轨迹的粗粒化分析模型,一方面,能够将高维空间抽象的生物功能构象变化动力学轨迹更加简单、直观的表示,另一方面,可以通过多条并行短轨迹预测长时间动力学,引入并行计算很大程度上缩减模拟所需要时间。近日,香港科技大学黄旭辉教授课题组总结了近几年MSM领域地重要进展与研究成果并对未来做出了展望。该论文目前已发表在JACS Au。分子动力学模拟(Molecular Dynamics Simulation)可以用来获得生物大分子等活性物质的全原子精细构象动力学信息,从而揭示生物大分子复杂的构象变化动力学过程。然而,对于复杂的生物体系而言,其大分子发挥相关功能的构象变化动力学所跨越的时间尺度(毫秒量级甚至更大)相比于受到计算机算力所限制的分子动力学模拟方法(微秒量级或更小)往往是要大很多的,甚至跨越几个数量级。因此,在近十几年的工作中,人们不断发展、优化基于分子动力学模拟的马尔科夫态模型——通过分析大量的短的分子动力学模拟轨迹,来预测长时间尺度的复杂生物大分子的重要功能构象变化动力学。马尔科夫态模型的核心方法是通过对时间与空间进行粗粒化处理,在离散的时间序列上建立起离散态的动力学过程,并根据马尔科夫链的演化(与过去信息无关),得到长时间尺度的动力学信息。在MSM中,将相空间进行分为大量小态或多个亚稳态(一般先通过K-Center、K-Means、K-Medoids等聚类算法将空间分多个小态,后通过PCCA、 PCCA+等组合算法重组至大态)。空间上的降维或离散化会破坏分子动力学原有的Markovian性质,如果可以将快过程和慢过程很好的分离,在间隔时间(lag-time)大于快过程时间后,慢过程仍然具有Markovian性质。通过对大量离散化分子动力学轨迹进行采样,可以计算出态与态之间的迁移概率,得到固定间隔时间下的迁移概率矩阵,并最终获得预测体系长时间动力学的演化方程: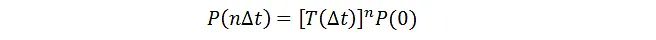
因此,基于分子动力学模拟数据完整构建MSM的整个过程大概可以分为以下几步:Feature Selection - Dimensionality Reduction - Discretization - Lumping。在该文中,作者从两个方面介绍MSM领域中的最新进展。(1)引入深度学习算法:实现高效、自动化的Feature Selection以及Dimensionality Reduction; (2)利用广义主方程理论:计算投影空间动力学过程中的记忆内核,通过更短的轨迹更准确预测长时间动力学过程。深度学习算法用于Feature Selection & Dimensionality ReductionFeature Selection 可以确定构建MSM的必要自由度和基函数。一般来说,对于体系较小的生物分子(如NTL9,FIP35 WW domain),可以使用整个分子的结构特征构造MSM,获得全局的构象变化动力学信息。然而,对于复杂的生物大分子体系(例如Pol Ⅱ复合物,约3600个氨基酸残基,将近1300万组α-C间距),保留所有特征来构造MSM消耗大量计算资源,并且只有局部功能相关的构象变化动力学才是研究重点。在早期的研究中,一般通过对体系的理解或物理直觉来筛选特征。近年来,逐渐发展出一些自动化实现Feature Selection的方法。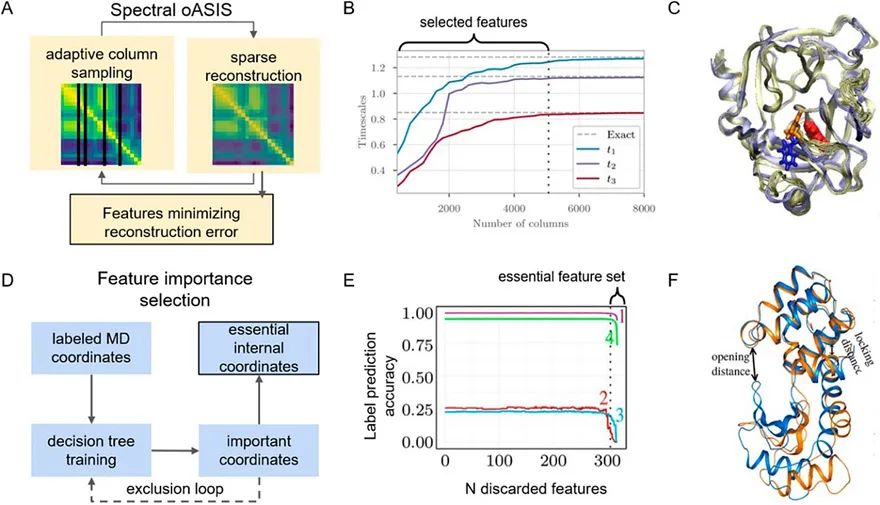
图1. 用于研究大分子功能构象变化动力学所使用的Feature Selection方法。A)Spectral-oASIS算法;B)对于胰蛋白酶-苯甲脒体系利用Spectral-oASIS方法筛选特征,时间尺度同特征数量变化曲线;C)利用Spectral-oASIS 方法对胰蛋白酶苯甲脒活性位点开放过程选择特征并进行表示;D) 重要特征筛选方法概括;E)将T4溶菌酶原始轨迹分类到不同亚稳态的精确度与被舍弃的特征变量数量之间的相关曲线;F)提取出的ECs用来表示T4溶菌酶的功能构象变化结构。Spectral-oASIS是由Frank Noe教授与Cecilia Clementi教授课题组在2018年提出的实现自动化Feature Selection的方法 [1]。该方法在生物大分子系统所有特征集合中采样并进行筛选,利用Nystrom算法,构建近似的弛豫协方差矩阵,并计算相应的特征值,通过变分原理找到能够最佳近似得到体系重要动力学过程的集合(图1A,B)。除此之外,Gerhard Stoke教授课题组在18年也发展了一种基于深度学习算法的实现自动化Feature Selection的方法[2] ——重要特征筛选(feature importance selection)方法。该方法基于决策树结构的监督机器学习算法,首先将原始轨迹的坐标集合作为变量,相对应的亚稳态分类作为标签,不断训练、优化模型,提取出对分态影响较大的重要特征。之后在这些特征所构成的集合中继续筛选、迭代、计算分类时的精确程度,进而得到与生物大分子局部功能构象变化紧密相关的重要特征变量(essential internal coordinates(ECs))(图1D,E)。2. Dimensionality Reduction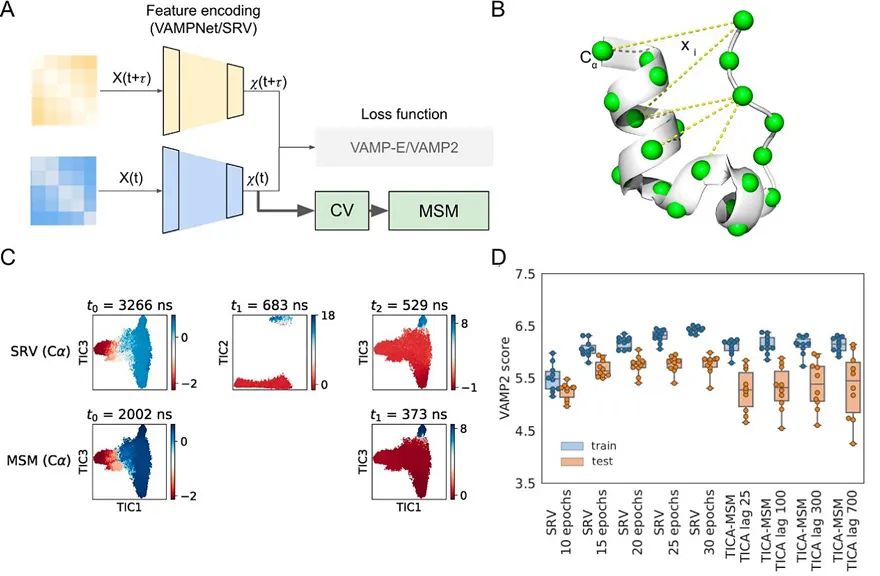
图2. 基于VAMPNets及其衍生方法所得到CVs可以准确描述体系重要动力学信息。A)VAMPNets结构示意图;B)Trp-笼蛋白结构;C)将Trp-笼蛋白的MD模拟轨迹投影到TICA坐标上,上三张图用颜色标记部分是投影在TICA空间的由SRV方法得到的三个动力学模式,下面两张图用颜色标记部分是投影在TICA空间的由TICA-MSM方法得到的两个动力学模式;D)根据VAMP-2 score对不同方法进行评估。为了构建MSM,需要将相空间进行离散化,但在高维空间直接进行离散化分态很困难。一般来说,人们通过提取出系统相互正交的最慢的动力学模式作为体系的Collective Variables(CVs),并将高维空间的分子动力学轨迹投影到这些CVs上,从而在尽量保留原始重要动力学信息的同时实现降维。近年来,基于变分原理(Variational Principle)的TICA方法(Time-Lagged Independent Components Analysis)常被用来计算体系前几个最慢的动力学模式,作为CVs来进行空间降维。2018年, Frank Noe教授课题组结合深度学习算法和变分原理提出了VAMPNet的概念,可以用于计算高维空间的最慢的动力学模式,进而构造MSM [3]。该方法采用了两个并行的深度学习网络,分别将高维相空间的即时分子动力学轨迹与时间弛豫轨迹作为网络的输入部分,根据变分原理设计VAMP-2 Score(R2)作为深度学习网络的损失函数,通过梯度下降算法不断训练优化参数,最终得到根据原始特征非线性重组后的CVs(图2A)。然而,由于VAMPNet是基于Koopman理论所建立的,该方法所研究的体系并不包含精细平衡(detailed balance)的限制条件。因此,在2019年,Andrew L. Ferguson教授课题组又在VAMPNet的基础上提出了SRV理论(State-free Reversible VAMPNets),并加入了系统动力学可逆的限制条件。在此工作中,SRV理论被成功用于构建研究Trp-笼蛋白折叠动力学的MSM。该方法将蛋白的所有α-C间距作为神经网络的输入部分(图2B),通过训练优化SRV网络,得到该体系的前七个CVs,并在这七个CVs构成的低维空间中,继续进行分态并构建MSM。相比于TICA,SRV方法计算出了TICA未能得到的一个动力学过程(图2C),并且得到了更加接近真实动力学模式的CVs(图2D)。利用广义主方程理论:计算投影空间动力学过程中的记忆内核低维空间的运动轨迹往往需要足够长的lag-time(受到较短的分子动力学轨迹长度所限制)才能达到Markovian。为了解决这一问题,2019年,黄旭辉教授课题组利用广义主方程发展了准马尔科夫态模型算法(quasi-Markov State Models, qMSM)可广泛用于复杂生物体系精确动力学计算 [4]。低维离散投影空间的广义主方程表示形式:
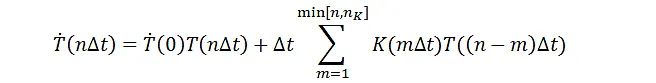
相比于传统的马尔科夫模型,基于广义主方程发展的准马尔科夫态模型引入了记忆内核K(mΔt)(Memory Kernel),可以准确计算在投影空间中历史动力学对现在动力学的影响。其中,记忆核K(mΔt)可以由转移概率矩阵及其微分形式通过贪心算法得到,并会在m足够大(间隔时间足够长)时衰减为零。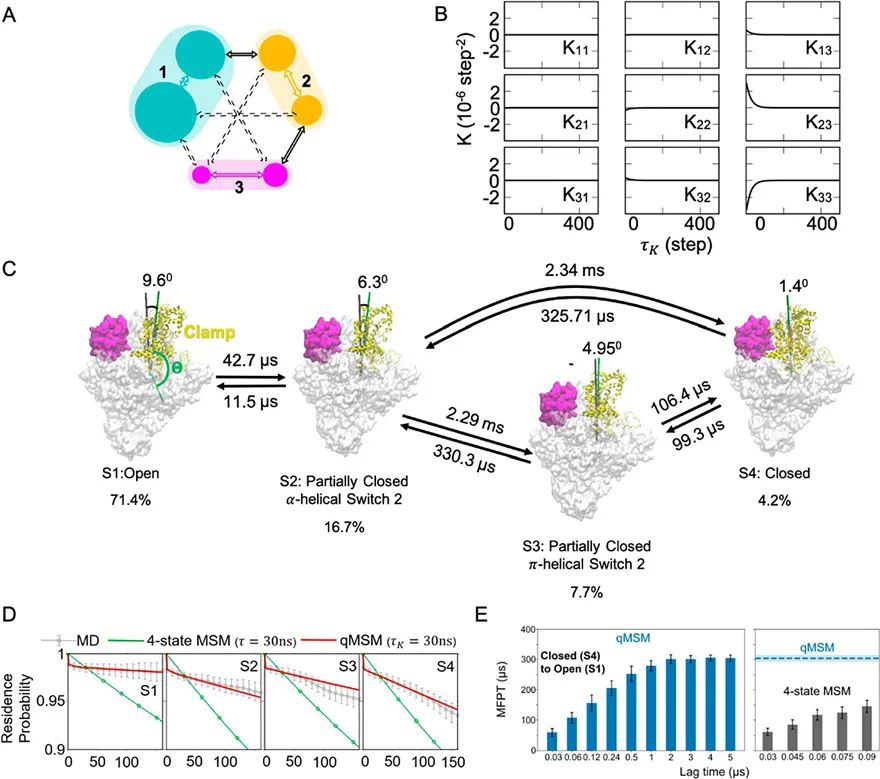
图3. qMSM理论根据已有分态获得的精准动力学模型。A) 简单三态模型;B)三态模型中的记忆内核;C)靶向细菌RNA聚合酶clamp区域打开过程中四个亚稳态之间的动力学转化过程以及qMSM计算的平均转换时间;D) Chapman−Kolmogorov 测试;E)构象亚稳态S4到S1的Mean First Passage Time (MFPT)。利用qMSM,黄教授课题组成功揭示了靶向细菌RNA聚合酶的抗生素抑制基因转录的机理。在计算RNA聚合酶的构象转变动力学模型时,基于广义主方程的qMSM可以得到比MSM更好的结果。比如,在间隔时间为30 ns的情况下,qMSM能够更精准的预测体系的快动力学过程(图3D)。并且,亚稳态S4-亚稳态S1过程所需的时间时,qMSM在更加短的间隔时间下得到了更接近于真实系统的MFPT(图3C、E)。除该工作之外,马里兰大学Tiwary教授课题组又建立了另一套基于LSTM模型(Long Short-Term Memory)的算法用于研究生物大分子体系构象变化动力学过程。该算法通过构建循环神经网络(Recurrent Neural Network),在不同时间节点下保留过去的信息,并将路径熵作为损失函数,成功预测了丙二酸二肽的动力学过程,以及实验单分子FRET数据。这篇文章总结了机器学习算法在马尔科夫态模型理论中的应用,通过引入机器学习算法,可以有效的进行动力学过程的特征选择和相空间的降维。利用统计力学中的广义主方程,可以利用短的动力学轨迹更加准确地预测长时间动力学过程。将计算机科学中的不同算法与物理化学理论结合往往能够产生不一样的火花。Markov State Models to Study the Functional Dynamics of Proteins in the Wake of Machine LearningKirill A. Konovalov, Ilona Christy Unarta, Siqin Cao, Eshani C. Goonetilleke, and Xuhui Huang*JACS Au, 2021, DOI: 10.1021/jacsau.1c00254
https://www.x-mol.com/university/faculty/304555[1]. Litzinger, F.; Boninsegna, L.; Wu, H.; Nuske, F.; Patel, R.; Baraniuk, R.; Noe, F.; Clementi, C. Rapid Calculation of Molecular Kinetics Using Compressed Sensing. J. Chem. Theory Comput., 2018, 14 (5), 2771−2783.[2]. Brandt, S.; Sittel, F.; Ernst, M.; Stock, G. Machine Learning of Biomolecular Reaction Coordinates. J. Phys. Chem. Lett., 2018, 9 (9), 2144−2150.[3]. Mardt, A.; Pasquali, L.; Wu, H.; Noe, F. VAMPnets for deep learning of molecular kinetics. Nat. Commun., 2018, 9, 5.[4]. Cao, S. Q.; Montoya-Castillo, A.; Wang, W.; Markland, T. E.; Huang, X. H. On the advantages of exploiting memory in Markov state models for biomolecular dynamics. J. Chem. Phys., 2020, 153 (1), 014105.


点击“阅读原文”,查看 化学 • 材料 领域所有收录期刊
