数学推导+纯Python实现机器学习算法26：PCA降维

点击上方“小白学视觉”，选择加"星标"或“置顶”

重磅干货，第一时间送达

作为一种常见的多元统计分析方法，主成分分析法（Principal Component Analysis，PCA）也是一种经典的无监督学习算法。PCA通过正交变换将一组由线性相关变量表示的数据转换为少数几个由线性无关变量表示的数据，这几个线性无关的变量就是主成分。PCA通过将高维数据维度减少到少数几个维度，本质上属于一种数据降维方法，也可以用来探索数据的内在结构。

PCA原理与推导

PCA的基本想法如下：首先对需要降维的数据各个变量标准化（规范化）为均值为0、方差为1的数据集。然后对标准化后的数据进行正交变换，将原来的数据转换为若干个线性无关的向量表示的新数据。这些新向量表示的数据不仅要求相互线性无关，而且需要是所包含的信息量最大。

PCA使用方差来衡量新变量的信息量大小，按照方差大小排序依次为第一主成分、第二主成分等。下面对PCA原理进行简单推导。假设原始数据为维随机变量，其均值向量为：

其协方差矩阵为 :

现假设由维随机变量到维随机变量的线性变换：
其中。

然后可得变换后的随机变量的统计特征：

当上述线性变换满足如下条件时，变换后的分别为的第一主成分、第二主成分以及第主成分。

变换的系数向量为单位向量，有。
变换后的变量与线性无关，即。
变量是所有线性变换中方差最大的，是与不相关的所有线性变换中方差最大的。

以上条件给出了求解PCA主成分的方法。根据约束条件和优化目标，我们可以使用拉格朗日乘子法来求出主成分。先来求解第一主成分。

根据前述条件，我们可以形式化第一主成分的数学表达为：

定义拉格朗日函数：

将上述拉格朗日函数对求导并令为0可得：

所以是的特征值，是对应的单位特征向量。假设是的最大特征值对应的单位特征向量，则和均为上述优化问题的最优解。所以为第一主成分，其方差为对应协方差矩阵的最大特征值：

同样方法也可求第二主成分。但约束条件中需要加上与第一主成分不相关的约束，具体推导这里略过。按上述方法可一致计算到第个主成分，且第个主成分的方差等于的第个特征值：

假设原始数据为行列的数据，梳理PCA的计算流程如下：

对行列的数据按照列进行均值为0方差为1的标准化；
计算标准化后的的协方差矩阵；
计算协方差矩阵的特征值和对应的特征向量；
将特征向量按对应特征值大小从上到下按行排列成矩阵，取前行构成的矩阵；
即为PCA降维后的维数据。

PCA的numpy实现

虽然sklearn中提供了PCA降维的API，但其背后算法是用SVD来实现的。numpy模块下提供了强大的矩阵运算函数，下面我们用numpy来实现一个PCA算法。

import numpy as np
class PCA():    # 计算协方差矩阵    def calculate_covariance_matrix(self, X):        m = X.shape[0]        # 数据标准化        X = X - np.mean(X, axis=0)        return 1 / m * np.matmul(X.T, X)



    
    def pca(self, X, n_components):        # 计算协方差矩阵        covariance_matrix = self.calculate_covariance_matrix(X)        # 计算协方差矩阵的特征值和对应特征向量        eigenvalues, eigenvectors = np.linalg.eig(covariance_matrix)        # 对特征值排序        idx = eigenvalues.argsort()[::-1]        # 取最大的前n_component组        eigenvectors = eigenvectors[:, idx]        eigenvectors = eigenvectors[:, :n_components]        # Y=PX转换        return np.matmul(X, eigenvectors)

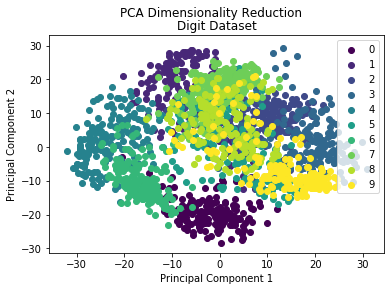
由上述代码可以看到，基于numpy我们仅需要数行核心代码即可实现一个PCA降维算法。下面以sklearn digits数据集为例看一下降维效果：

from sklearn import datasetsimport matplotlib.pyplot as pltimport matplotlib.cm as cmximport matplotlib.colors as colors
# 导入sklearn数据集data = datasets.load_digits()X = data.datay = data.target
# 将数据降维到2个主成分X_trans = PCA().pca(X, 2)x1 = X_trans[:, 0]x2 = X_trans[:, 1]
# 绘图展示cmap = plt.get_cmap('viridis')colors = [cmap(i) for i in np.linspace(0, 1, len(np.unique(y)))]
class_distr = []# 绘制不同类别分别for i, l in enumerate(np.unique(y)):    _x1 = x1[y == l]    _x2 = x2[y == l]    _y = y[y == l]    class_distr.append(plt.scatter(_x1, _x2, color=colors[i]))
# 图例plt.legend(class_distr, y, loc=1)
# 坐标轴plt.suptitle("PCA Dimensionality Reduction")plt.title("Digit Dataset")plt.xlabel('Principal Component 1')plt.ylabel('Principal Component 2')plt.show();

下载1：OpenCV-Contrib扩展模块中文版教程

在「小白学视觉」公众号后台回复：扩展模块中文教程，即可下载全网第一份OpenCV扩展模块教程中文版，涵盖扩展模块安装、SFM算法、立体视觉、目标跟踪、生物视觉、超分辨率处理等二十多章内容。

下载2：Python视觉实战项目52讲

在「小白学视觉」公众号后台回复：Python视觉实战项目，即可下载包括图像分割、口罩检测、车道线检测、车辆计数、添加眼线、车牌识别、字符识别、情绪检测、文本内容提取、面部识别等31个视觉实战项目，助力快速学校计算机视觉。

下载3：OpenCV实战项目20讲

在「小白学视觉」公众号后台回复：OpenCV实战项目20讲 ，即可下载含有20个基于OpenCV实现20个实战项目，实现OpenCV学习进阶。

交流群

欢迎加入公众号读者群一起和同行交流，目前有SLAM、三维视觉、传感器、自动驾驶、计算摄影、检测、分割、识别、医学影像、GAN、算法竞赛等微信群（以后会逐渐细分），请扫描下面微信号加群，备注：”昵称+学校/公司+研究方向“，例如：”张三 + 上海交大 + 视觉SLAM“。请按照格式备注，否则不予通过。添加成功后会根据研究方向邀请进入相关微信群。请勿在群内发送广告，否则会请出群，谢谢理解~