作者：Andrej Karpathy
译者：Yang
原文标题：Deep Neural Nets: 33 years ago and 33 years from now
Andrej Karpathy，斯坦福大学博士（师从李飞飞）、前 OpenAI 研究科学家，现为特斯拉人工智能和自动驾驶视觉总监。
个人网站主页：https://karpathy.ai/
图 | Andrej Karpathy 特斯拉人工智能和自动驾驶视觉总监我认为 Yann LeCun 等人于 1989 年发表的论文“反向传播应用于手写邮政编码识别”（Backpropagation Applied to Handwritten Zip Code Recognition），具有相当重要的历史意义，因为据我所知，这是最早用反向传播机制端到端训练的神经网络在现实生活中的应用。除了其使用的微型数据集（7291 个 16x16 的灰度数字图像）和微型神经网络（仅 1000 个神经元）显得落伍之外，在 33 年后的今天，这篇论文读来仍然十分新颖——它展示了一个数据集，描述了神经网络结构、损失函数、优化器，并报告了在训练集和测试集上实验得到的错误率。除了时光已流逝 33 年，这篇文章仍是一篇标准的深度学习论文。因此，我此次复现这篇论文，一是为了好玩，二是将这次练习作为一个案例来研究深度学习进展的本质。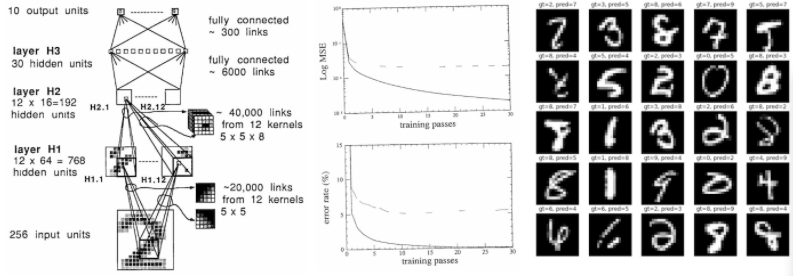
我试着尽可能与这篇论文保持一致，并用 PyTorch 复现了 GitHub repo 上 karpathy/lecun1989-repro 中的所有内容。最初的网络部署在 Lisp 上，使用 Bottou 和 LeCun 1988 年发表的“backpropagation simulator SN（后来命名为 Lush）”。这篇论文是用法语写的，所以我没有更好地理解它，但从结构上来看，你可以使用更高级的 API 来构造神经网络，就像你今天在 PyTorch 上搭建各式各样的项目那样。作为软件设计的简要说明，现代程序库采用了一种分为 3 部分的设计：1）一个高速（C/CUDA）通用张量库，能在多维张量上实现基本的数学运算；
2）一个自动求导引擎，能跟踪正向计算特征，并能提供反向传播操作；
3）可编程（Python）的深度学习编码器，高级的 API，需要包含常见的深度学习操作，比如构建层、架构、提供优化器、损失函数等。
训练细节在训练过程中，我们必须在有 7291 个示例的训练集上训练 23 个周期，总共向神经网络传送了 167693 次数据（包含样本和标签）。最初的网络在 SUN-4/260 工作站上训练了 3 天。我在我的 MacBook Air（M1）CPU 上运行了我的实现，并在大约 90 秒的时间内完成了运行（约 3000 倍的显著提速）。我的 conda 设置为使用本机 AMD64 版本，而不是 Rosetta 仿真。如果 Pytorch 支持 M 1（包括 GPU 和 NPU）的全部功能，加速可能会更显著，但这似乎仍在开发中。我还天真地尝试在一张 A100 GPU 上运行代码，但实际上训练速度更慢了，很可能是因为网络太小了（4 个卷积层，最多 12 个通道，总共 9760 个参数，64 K 位址量，1 K 激活值），SGD 每次只能使用一个样本。这就是说，如果真的想用现代硬件（A100）和软件基础设施（CUDA、PyTorch）解决这个问题，我们需要用每个样本的 SGD 过程来交换完整的批量训练，以最大限度地提高 GPU 利用率，并很可能实现另一个约 100 倍的训练耗时提速。
复现 1989 年的表现 原论文展示的结果如下：
eval: split train. loss 2.5e-3. error 0.14%. misses: 10
eval: split test . loss 1.8e-2. error 5.00%. misses: 102
而我的复现代码在同时期的表现如下：
eval: split train. loss 4.073383e-03. error 0.62%. misses: 45
eval: split test . loss 2.838382e-02. error 4.09%. misses: 82
由此可见，我只能粗略地再现这些结果，却不能做到完全一样。可悲的是，很可能永远无法进行精确复现了，因为我认为原始数据集已经被遗弃在了时间的长河中。相反，我不得不使用更大的 MNIST 数据集（哈哈，我从没想过我会用“大”来形容它）来模拟它，取其 28x28 位，通过双线性插值将其缩小到 16x16 像素，并随机地从中提取合理数量的训练集和测试集样本。但我相信还有其他罪魁祸首。例如，这篇论文对权重初始化方案的描述有点过于抽象，我怀疑 PDF 文件中存在一些格式错误，例如，删除点“.”让“2.5”看起来像“2 5”，并且有可能（我想是吧？）删除了平方根。例如，我们被告知权重初始值是从均匀的“2 4/F”中提取的，其中 F 是扇入，但我猜这肯定是（我猜的）指“2.4/sqrt（F）”，其中 sqrt 有助于保持输出的标准偏差。网络的 H1 层和 H2 层之间的特定稀疏连接结构也被忽略了，论文只是说它是“根据一个在这里不会被讨论的方案选择的”，所以我不得不在这里做出一些合理的猜测，比如使用重叠块稀疏结构。论文还声称使用了 tanh 非线性，但我想这实际上可能是映射 ntanh（1）=1 的“标准化 tanh”，并可能添加了一个按比例缩小的跳跃连接，这是在当时很流行的操作，以确保 tanh 平滑的尾部至少有一点梯度。最后，本文使用了“牛顿算法的一个特殊版本，它使用了 Hessian 的正对角近似值”，但我只使用了 SGD，因为它非常简单，更何况根据本文，“人们认为该算法不会带来学习速度的巨大提高”。
坐上时光车“作弊”
这是我最喜欢的部分。想一下，相比于 1989，我们已经在未来生活了 33 年，这时的深度学习是一个非常火爆的研究领域。利用我们的现代理解和 33 年来的研发技术积累，我们能在原有成果的基础上提高多少？我最初的结果是：
eval: split train. loss 4.073383e-03. error 0.62%. misses: 45
eval: split test . loss 2.838382e-02. error 4.09%. misses: 82
首先我略述一下，我们正在做一个 10 类别的简单分类任务，但在当时，这被建模成一个均方误差（MSE）回归到目标 -1（负类）或 +1（正类）的任务，输出神经元同样也具有 tanh 非线性。所以我删除了输出层上的 tanh 以获得类别 logit，并在标准（多类）交叉熵损失函数中交换。这一变化极大地改善了训练错误，在训练集上直接过拟合了，结果如下：
eval: split train. loss 9.536698e-06. error 0.00%. misses: 0
eval: split test . loss 9.536698e-06. error 4.38%. misses: 87
我怀疑，如果输出层具有（饱和）tanh 非线性和 MSE 误差，那么在权重初始化细节上必须更加小心。其次，根据我的经验，一个经过微调的 SGD 可以很好地工作，但现代的 Adam 优化器（当然，学习率为 3e-4）几乎总是作为一个强大的 baseline，几乎不需要任何调整。因此，为了提高我对优化不会影响性能的信心，我选择了使用学习率为 3e-4 的 AdamW，并在训练过程中逐步将其降至 1e-4，结果如下：
eval: split train. loss 0.000000e+00. error 0.00%. misses: 0
eval: split test . loss 0.000000e+00. error 3.59%. misses: 72
这在 SGD 的基础上给出了一个略微改善的结果，但我们还必须记住，通过默认参数，训练过程中也出现了一些权重衰减，这有助于克服过度拟合的情况。由于仍然出现了严重的过度拟合，我随后介绍了一种简单的数据增强策略，将输入图像水平或垂直移动最多 1 个像素。然而，由于这模拟了数据集大小的增加，我还必须将训练周期数数从 23 次增加到 60 次（我已经验证过在原始设置中单纯地增加通过次数并不能显著改善结果）：
eval: split train. loss 8.780676e-04. error 1.70%. misses: 123
eval: split test . loss 8.780676e-04. error 2.19%. misses: 43
从测试错误中可以看出，这很有帮助！数据增强是一个相当简单且非常标准的概念，用于克服过度拟合，但我在 1989 年的论文中没有找到它，也许它是一个 1989 年后才有的创新（我猜的）。由于我们仍然有点过拟合，我在工具箱中找到了另一个现代工具，Dropout。我在参数最多的层（H 3）前加了一个 0.25 的弱衰减。因为 dropout 将激活设置为零，所以将其与激活范围为 [-1,1] 的 tanh 一起使用没有多大意义，所以我也将所有非线性替换为更简单的 ReLU 激活函数。因为 dropout 在训练中会带来更多的噪音，我们还必须训练更长的时间，增加至最多 80 个训练周期，但结果却变得十分喜人：
eval: split train. loss 2.601336e-03. error 1.47%. misses: 106
eval: split test . loss 2.601336e-03. error 1.59%. misses: 32
这使得我们在测试集上的错误减少到了 32/2007！我验证了在原来的网络中仅仅交换 tanh->relu 并没有带来实质性的收益，所以这里的大部分改进都来自于增加了 dropout。总之，如果我能时光旅行到 1989 年，我将能够减少大约 60% 的错误率，使我们从约 80 个错误减少到约 30 个错误，测试集的总体错误率约为 1.5%。这并不是完全没有代价的，因为我们还将训练时间增加了近 4 倍，这将使 1989 年的训练时间从 3 天增加到近 12 天。但推理速度不会受到影响。剩下的测试失败样本如下所示：
然而，在替换 MSE->Softmax，SGD->AdamW，添加数据增强，dropout，交换 tanh→relu 之后，我开始逐渐减少依赖触手可得的技巧。我尝试了更多的方法（例如权重标准化），但没有得到更好的结果。我还尝试将 Visual Transformer（ViT）小型化为“micro-ViT”，大致在参数量和计算量上与之前相符，但无法仿真 convnet 的性能。当然，在过去的 33 年里，我们还研究出了许多其他创新，但其中许多创新（例如，残差连接，层/批次标准化）只适用于更大的模型，并且大多有助于稳定大规模优化。在这一点上，进一步的收益可能来自网络规模的扩大，但这会增加测试的推断时间。
用数据“作弊”另一种提高性能的方法是扩大数据集的规模，尽管完成数据标注需要一些成本。我们在最初的 baseline（再次作为消融参考）上测试结果是：
eval: split train. loss 4.073383e-03. error 0.62%. misses: 45
eval: split test . loss 2.838382e-02. error 4.09%. misses: 82
根据我们所有的 MNIST 都可用的事实，我们可以简单地尝试将训练集扩大 7 倍（从 7291 到 50000 个示例）。让 baseline 训练 100 个周期，这已经表明仅仅增加数据就能提高性能：
eval: split train. loss 1.305315e-02. error 2.03%. misses: 60
eval: split test . loss 1.943992e-02. error 2.74%. misses: 54
但进一步将其与当代知识的创新（如前一节所述）结合在一起，将带来迄今为止最好的表现：
eval: split train. loss 3.238392e-04. error 1.07%. misses: 31
eval: split test . loss 3.238392e-04. error 1.25%. misses: 24
总而言之，在 1989 年简单地扩展数据集将是提高系统性能的有效方法，且不需要牺牲推理时间。反思让我们总结一下我们在 2022 年时，作为一名时间旅行者考察 1989 年最先进的深度学习技术时所学到的：
首先，33 年来宏观层面上没有太大变化。我们仍在建立由神经元层组成的可微神经网络结构，并通过反向传播和随机梯度下降对其进行端到端优化。所有的东西读起来都非常熟悉，只是 1989 时它们的体量比较小。
按照今天的标准，1989 年的数据集就是一个“婴儿”：训练集只有 7291 个 16x16 的灰度图像。今天的视觉数据集通常包含数亿张来自网络的高分辨率彩色图像（例如，谷歌有 JFT-300M，OpenAI CLIP 是在 400M 的数据集上训练的），但仍会增长到几十亿。这大约是此前每幅图像约一千倍的像素信息（384*384*3/（16*16））乘以十万倍的图像数（1e9/1e4），输入的像素数据的差距约为一亿倍。
那时的神经网络也是一个“婴儿”：这个 1989 年的网络有大约 9760 个参数、64 K 个位址和 1 K 个激活值。现代（视觉）神经网络的规模通常有几十亿个小参数（1000000X）和 O（~1e12）个位址数（~1000000X），而自然语言模型甚至可以达到数万亿级别的参数量。
最先进的分类器花了 3 天时间在工作站上训练，而现在在我的无风扇笔记本电脑上训练只需 90 秒（3000 倍原始提速），通过切换到全批量优化并使用 GPU，很可能能进一步获得 100 倍的提升。
事实上，我能够根据现代的技术创新调整模型，比如使用数据增强，更好的损失函数和优化器，以将错误率降低 60%，同时保持数据集和模型的测试时间不变。
仅通过增大数据集就可以获得适度的收益。
进一步的显著收益可能来自更大的模型，这将需要更多的计算成本和额外的研发，以帮助在不断扩大的规模上稳定训练。值得一提的是，如果我被传送到 1989 年，我最终会在没有更强大计算机的情况下，使模型达到改进能力的上限。
假设这个练习的收获在时间维度上保持不变。2022 年的深度学习意味着什么？2055 年的时间旅行者会如何看待当前网络的性能？
2055 年的神经网络在宏观层面上与 2022 年的神经网络基本相同，只是更大。
我们今天的数据集和模型看起来像个笑话。两者都在大约上千亿倍大于当前数据集和模型。
我们可以在个人电脑设备上用大约一分钟的时间来训练 2022 年最先进的模型，这将成为一个有趣的周末项目。
今天的模型并不是最优的，只要改变模型的一些细节，损失函数，数据增强或优化器，我们就可以将误差减半。
我们的数据集太小，仅通过扩大数据集的规模就可以获得适度的收益。
如果不升级运算设备，并投资一些研发，以有效地训练如此规模的模型，就不可能取得进一步的收益。
但我想说的最重要的趋势是，在某些目标任务（如数字识别）上从头开始训练一个神经网络的整个过程由于过于精细化而很快变得过时，特别是随着 GPT 等基础模型的出现。这些基础模型只由少数具有大量计算资源的机构来训练，并且大多数应用是通过轻量级的微调网络，快速部署工程，数据清洗，模型蒸馏，用专用的推理网络来实现的。我认为，我们应该期待这一趋势愈发蓬勃，而且也已经确实如此。
在最极端的推断中，你根本不会想训练任何神经网络。在 2055 年，你将要求一个千亿大小的神经网络超强大脑通过用英语说话（或思考）来执行一些任务。如果你的要求足够清晰，它会很乐意执行的。当然，你也可以自己训练神经网络……但你还有什么训练的必要呢？
原文链接：
http://karpathy.github.io/2022/03/14/lecun1989/
