量化投资与机器学习微信公众号，是业内垂直于量化投资、对冲基金、Fintech、人工智能、大数据等领域的主流自媒体。公众号拥有来自公募、私募、券商、期货、银行、保险、高校等行业30W+关注者，曾荣获AMMA优秀品牌力、优秀洞察力大奖，连续4年被腾讯云+社区评选为“年度最佳作者”。
这就教你如何真正使用因子数据！
量化投资与机器学习公众号从2022年开始，正式推出我们的网红大IP：因子日历
2024年《因子日历》已如期编写中~QIML一直在想，除了日历本身外还能改小伙伴带来点什么？因此，我们花了大半年时间对所有因子进行了复现，同时结合现有数据给出了250+个可对外计算的因子。如此，让日历和数据结合在一起，成为一个更加实用的学习工具！
那么今天，QIML会给大家一系列教程，为购买因子日历的读者介绍如何使用量化手段来挖掘和分析因子！
如需下载因子日历提供的数据，请大家在公众号后台进行下载获取。
操作方式如下：
1、因子筛选应与所用模型相匹配，若是线性因子模型，只需选用能评估因子与收益间线性关系的指标，如IC、Rank IC；若是机器学习类的非线性模型，最好选用能进一步评估非线性关系的指标，如 Chi-square 及 Carmer's V 等；2、本文主要测试了机器学习类的非线性模型所需的因子筛选指标，推荐使用 Cramer'V 和互信息，它们都能捕捉非线性关系；虽然因子和收益都是连续型变量，但也可以将它们离散化后再做测试，特别是因子尾部数据与收益的关系，极端数据往往有更强的预测能力。前言
在传统的多因子模型体系下，已经有一套相对成熟的因子检验和因子筛选流程，因子检验大多涉及因子的 IC 分析、收益率分析、换手率分析、板块分析等多个方面，是对单个因子做检验，判断其是否对收益有显著影响；因子筛选主要有逐步回归、主成分分析 PCA 等方法，是对批量因子做筛选，剔除冗余因子，降低因子间的相关性，因子检验得到的因子有效性程度也可以作为因子筛选的评价指标，用于剔除低效因子。而本文主要是站在机器学习视角介绍相关的因子筛选方法，即特征筛选方法，机器学习下的因子筛选主要是为了模型能有更好的预测效果、更强的泛化能力，其中也会涉及相应的评价指标和筛选规则，但指标和规则不再局限于简单的线性相关性和线性回归，也涵盖了很多非线性关系的考察。 在机器学习视角下，根据是否考虑因子间的冗余信息 redundancy 或是多重共线性的影响 substitution effects，可以将因子筛选分为单因子筛选和多因子筛选，单因子筛选通常是对单个因子做独立评价，然后再基于筛选规则选出排名靠前的部分因子，选出的因子集可能存在冗余信息；多因子筛选通常是逐个比较新因子在已选因子基础上带来的“增强”作用来决定该因子的去留，选出的因子集是对收益有最强解释力且因子间不相关的因子，传统的因子筛选多属于这类。 下文先重点介绍单因子筛选常用的评价指标，了解因子日历中的因子在这些评价指标上的排名情况，单因子筛选的筛选规则通常选的过滤法，即筛选出排名靠前的部分因子，本文就不再赘述。选用的评价指标有：方差、信息熵、F统计量、卡方检验、互信息，其中前两个指标在计算时不考虑收益 y 的信息，可称为非监督型评价指标，其余指标在计算时同时考虑了收益 y 的信息，可称为监督型评价指标。测试说明
▪ 因子预处理：MAD 异常值处理、行业中位数缺失值填充、市值行业中心化处理、标准化处理；前 3 步处理都在横截面上操作，第 4 步标准化处理可进行横截面或跨横截面操作；▪ 测试频率：月频，特征为因子值，标签为股票下个月收益率；▪ 有 2 种滚动测试的样本划分：① 横截面测试：以每个月末 t 横截面对应的行数据为样本，进行滚动测试；② 跨横截面测试：模拟模型滚动训练时时间窗的划分，在每个月末 t ，回溯过去 24 个月（包含当前月），以这个时间区间上的行数据为样本，进行滚动测试；▪ 因子预处理：提前剔除了缺失率高的因子，最终参与测试的因子数为 232 个。 非监督型评价指标只计算单个因子 x 自身的统计指标来用于因子筛选，不涉及标签 y 的信息，是对因子自身情况的评价，常用的统计指标有：缺失率、方差、信息熵等，下文重点介绍方差、信息熵。 方差衡量了变量的离散程度。如果某个因子的方差很小，说明该因子在所有样本上的取值都趋于相同，对样本没有区分度，对模型来说用处不大。计算方差时，因子预处理不做标准化处理，但会做归一化处理。 对比大类因子的平均方差情况，排名靠前的有估值因子>无形资产因子>规模因子>流动性因子，而且这些类因子（特别是规模因子）跨横截面后方差有些许降低（因子取值波动反而变小了）；常用的动量因子的方差排名相对靠后；波动型技术指标的方差受时间维度的影响较大，跨横截面后该类因子取值波动变得更大了。结合下面几幅图可知各大类因子中方差排名最靠前和排名最靠后的具体因子以及它们在分布图中的大致位置（最顶端的点和最底端的点），所有因子过去所有横截面的平均方差都在 0.025 以上。 信息熵衡量了变量所包含的平均信息量。可以用信息熵来衡量因子取值的混乱程度（反过来说是“纯度”），如果某个因子的信息熵很高，说明该因子取值相对混乱和丰富，不确定性高，而不是偏向于单一取值，能为模型提供的信息也多。在计算单个因子的信息熵时，先将因子按取值范围的 10% 分位间隔进行离散化处理，分为 10 组，各组内的频数不等，再基于如下公式计算信息熵，其中p(xi)为各组内的频率：对比大类因子的平均信息熵情况，排名靠前的有规模因子>财务质量因子-改进>成长因子>投资因子>流动性因子等，但各大类因子间的信息熵差距并不是很大。值得注意的是，所有大类因子的信息熵在跨横截面后都有所下降（占比小于0.5）。结合下面几幅图可知各大类因子中信息熵排名最靠前和排名最靠后的具体因子以及它们在分布图中的大致位置（最顶端的点和最底端的点）。当所有组内频数都一致，即p(xi)=0.1时，信息熵达到最大，取值约为 3.32，对数市值、营业利润相关因子的取值都接近该水平。
def _entropy(x, bins=None):
"""
calculate Shanon Entropy
"""
N = len(x)
x_ = x[~np.isnan(x)] # drop nan
if len(x_)<1:
return np.nan
if bins is None:
_,counts = np.unique(x_, return_counts=True)
else:
counts = np.histogram(x_, bins=bins)[0]
prob = counts[np.nonzero(counts)] / N
en = -np.sum(prob * np.log2(prob))
return en
计算监督型评价指标时除了考虑因子 x 的信息外，还会同时考虑收益 y 的信息，是对因子与收益间关系的评价，常用的统计指标有 F 统计量、Cramer' V值、互信息等，测试用的收益 y 为股票未来一个月的收益率。
F统计量
此处的 F 统计量通过对单个因子 x 与收益 y 进行一元线性回归得到，具体调用的 sklearn 中的 f_regression，该方法采用如下公式计算 x 与 y 之间的回归系数：E[(X[:, i] - mean(X[:, i])) * (y - mean(y))] / (std(X[:, i]) * std(y))，该公式本质上就是计算的 x 与 y 的 pearson 相关系数（也就是因子 IC 值），可以证明得到该相关系数的平方即为该回归方程的判定系数R^2（回归平方和与总离差平方和之比值 SSR/SST），最终的 F 统计量为：
回归中的 F 统计量通常用于检测回归方程整体的显著性，由于单变量回归只涉及一个回归系数，此时的 F 统计量衡量了因子 x 和收益 y 的关联程度，F 值越高，关联性越强，对应的 p 值可用于判定因子 x 和收益 y 的关系是否显著。为了消除不同横截面样本量的影响，下图中的 F 统计量都是经过归一化后的值。
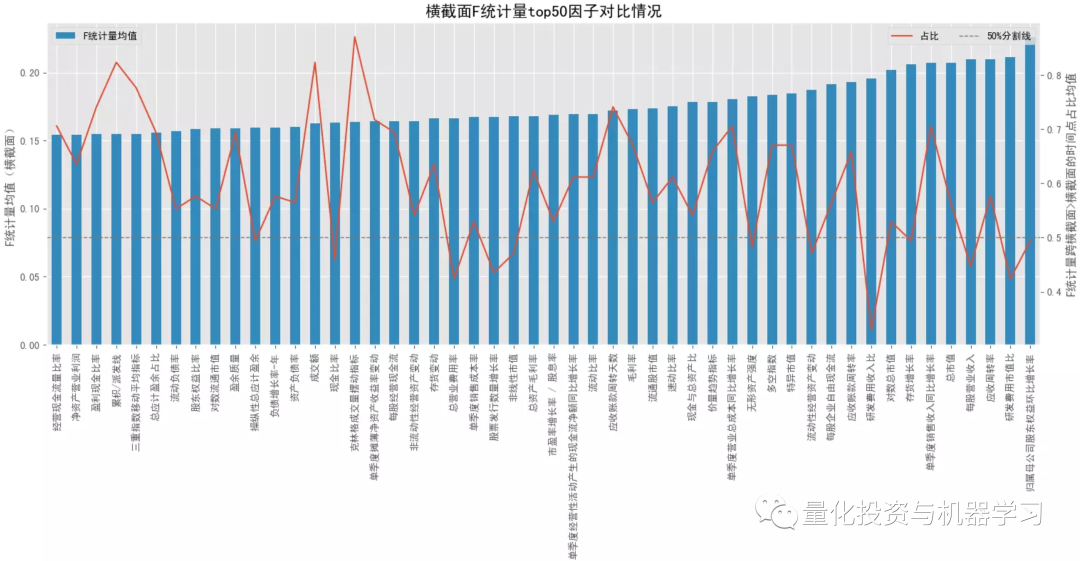
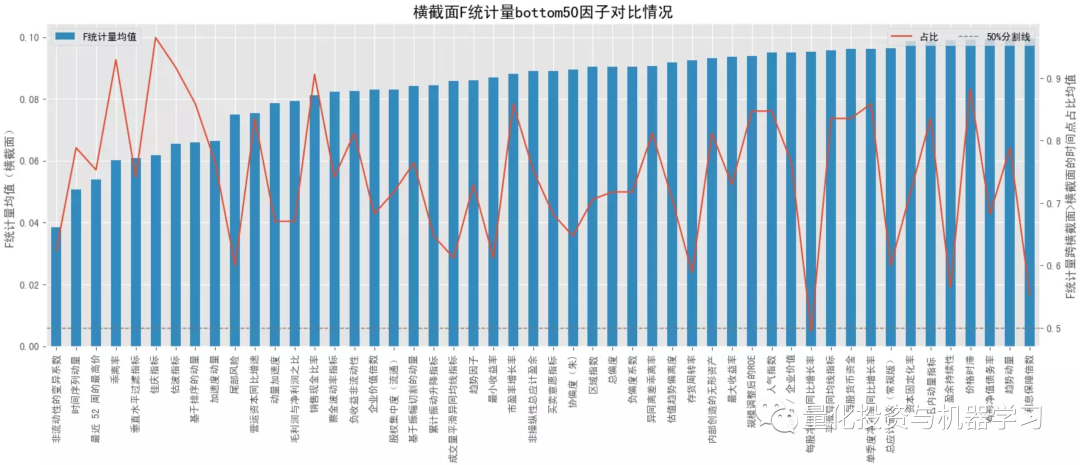
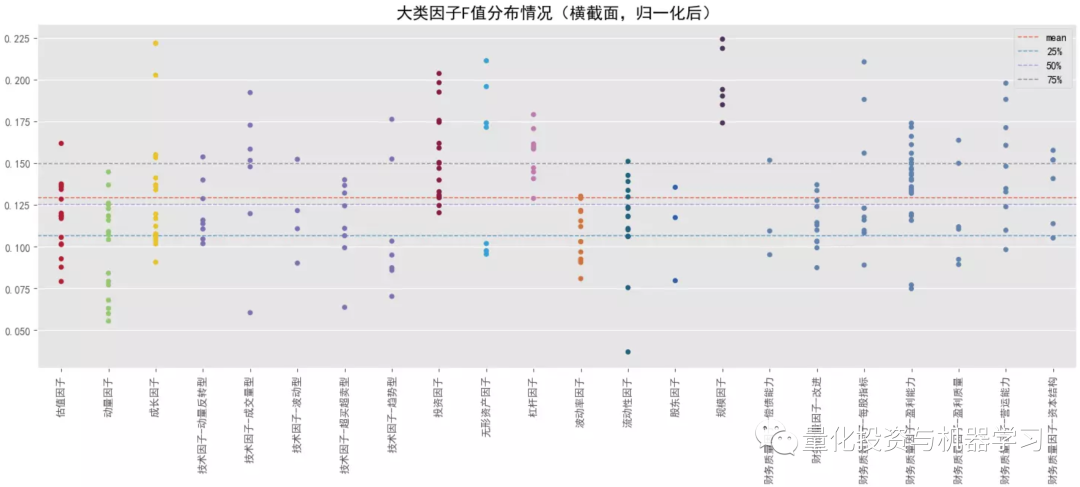
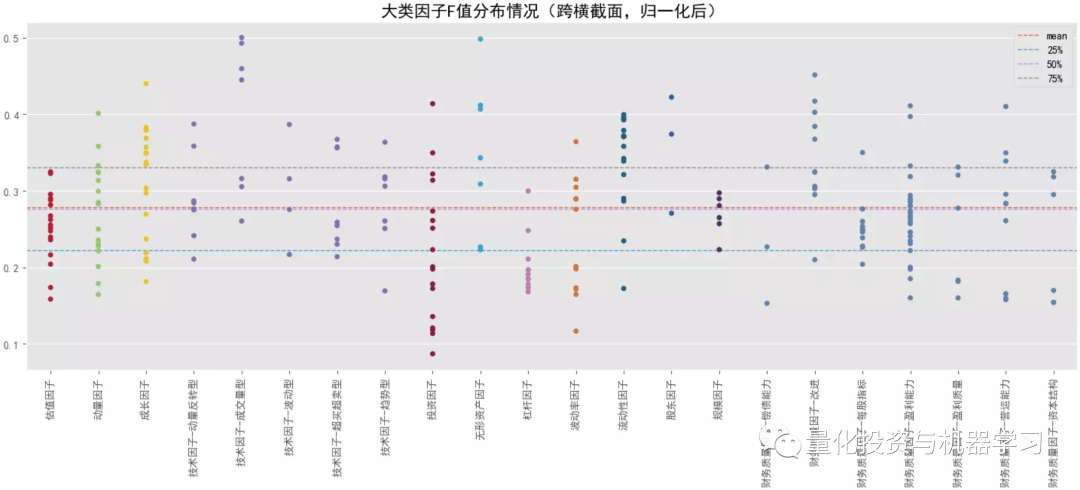
对比大类因子的平均 F 统计量情况，排名靠前的是规模因子>无形资产因子>投资因子>杠杆因子，常用的动量因子排名最后，估值因子也排名较后；基本上所有的大类因子在跨横截面后 F 统计量都有所提升（可能受样本量影响），但排名头部的大类因子提升的可能性相对更低些。在看 P 值显著占比情况，排名靠前的是规模因子>流动性因子>来自量价的技术因子、动量因子、波动率因子等，前面 F 值高的因子反倒排名靠后了，说明这些因子在不同横截面上的表现不是很稳定，有些时点上表现很突出，但大多数时间表现并不理想。
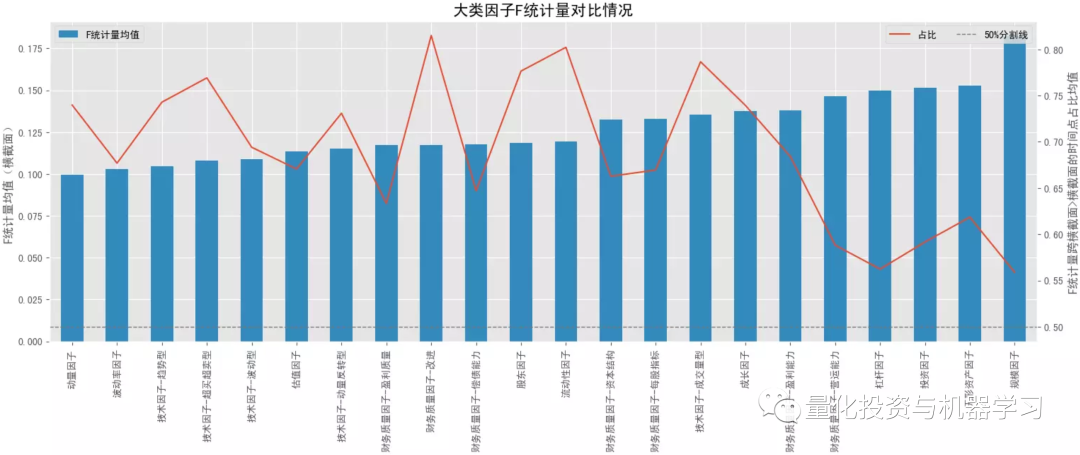
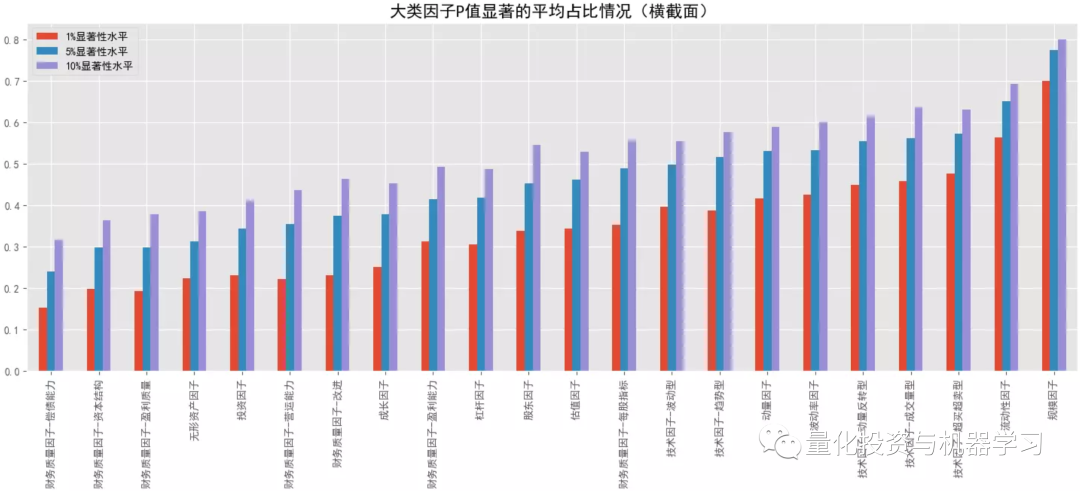
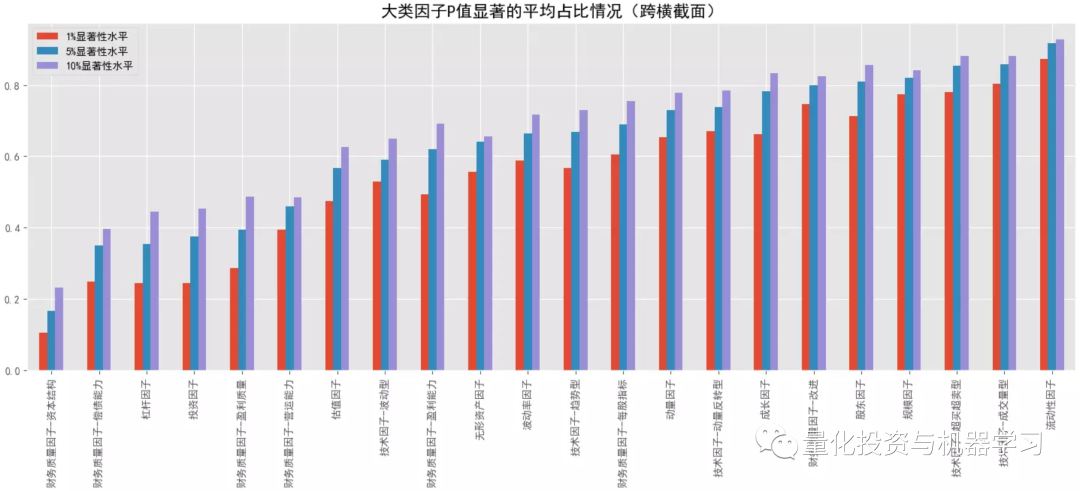
结合下面几幅图可知各大类因子中 F 统计量排名最靠前和排名最靠后的具体因子以及它们在分布图中的大致位置（最顶端的点和最底端的点）。与大类因子一致，就 F 值来看，排名靠前的因子中，基本面因子居多，排名靠后的因子中，量价因子居多，但量价因子在时序上表现的更稳定。
卡方检验
此处的卡方检验指的是 Pearson's chi squared test，它借助列联表来判断两个分类变量是否独立，所以若想用卡方检验来做因子筛选，需要对因子 x 和收益 y 做离散化处理，对于因子 x 的离散化有 2 种方式：① 离散化为 N 类：利用 qcut 等分为 N 组，组内样本量相等；② 离散化为 2 类：只取因子值排名靠前的 n% 样本作为一组和排名靠后的 n% 样本作为一组，剔除掉中间的那部分样本，只保留尾部 tail；对于收益 y 的离散化有 2 种方式：① 离散化为 N 类：利用 qcut 等分为 N 组，组内样本量相等；② 离散化为 2 类：将收益大于等于 0 的为一组，收益小于 0 的为一组。若 x 的划分选用的方式 ②，则保留相应的 y ，但 y 的分类是基于全样本确定的。对于评价指标，可以选用 Cramer'V 和 p 值：
在筛选因子时，一般用 Cramer'V ，其取值为 0-1，取值越高，关联性越强，更方便做比较。相比回归的 F 统计值，Cramer'V 能衡量因子 x 与收益 y 的非线性关系，而且因子 x 的尾部划分，能进一步知道因子的极端取值与收益的关系，而因子对收益的预测能力往往依赖于极端值。
卡方检验示例代码
def chi2(x, y, x_bin=0.1, y_bin=3) -> tuple:
'''
Chi-square test of independence between x and y
x_bin: int -> use all cases and split equally; 0 use tails only and get two bins
y_bin: int -> split equally; 'zero' -> split at zero and get only two bins (win and lose), y=0 belong to win
return：tuple (chi_square, p_value, contingency coefficient, cramer'v)
'''
x,y = discretization_processing(x, y, x_bin, y_bin)
# get chi2
arr = pd.crosstab(index=x, columns=y).sort_index().to_numpy()
chi2_stat = chi2_contingency(arr, correction=True, lambda_=None)
chi2 = chi2_stat[0]
phi2 = chi2 / arr.sum()
n_rows, n_cols = arr.shape
cramer = np.sqrt(phi2 / min(n_cols - 1, n_rows - 1))
contingency = np.sqrt(chi2 / (chi2+arr.sum()))
return (chi2,chi2_stat[1],contingency,cramer)
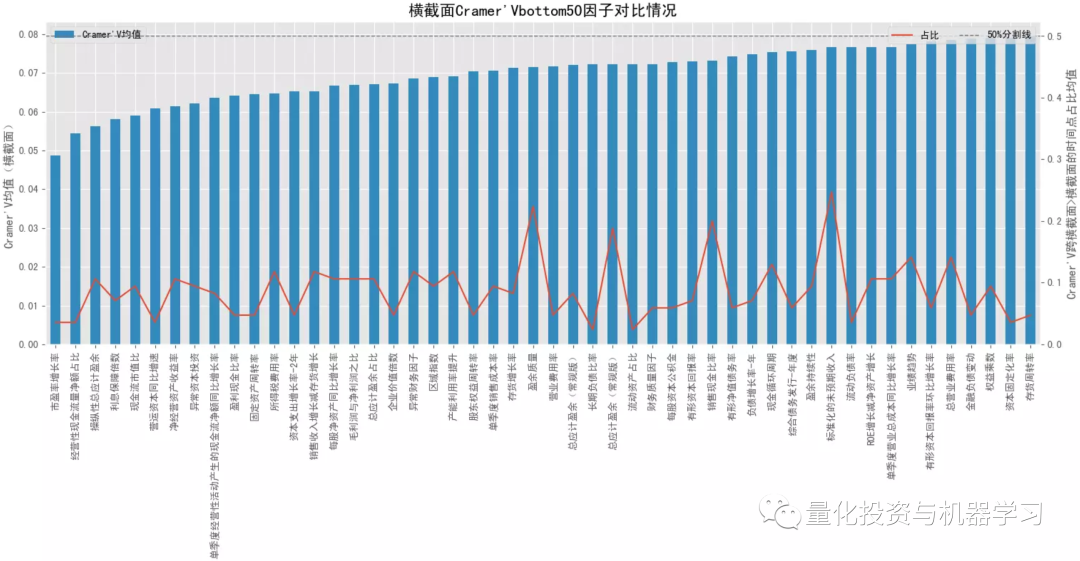
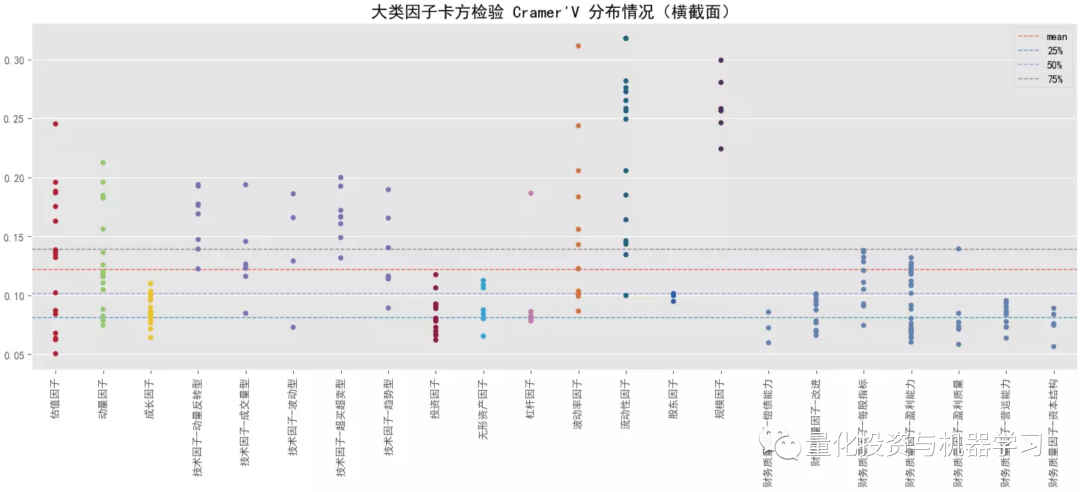
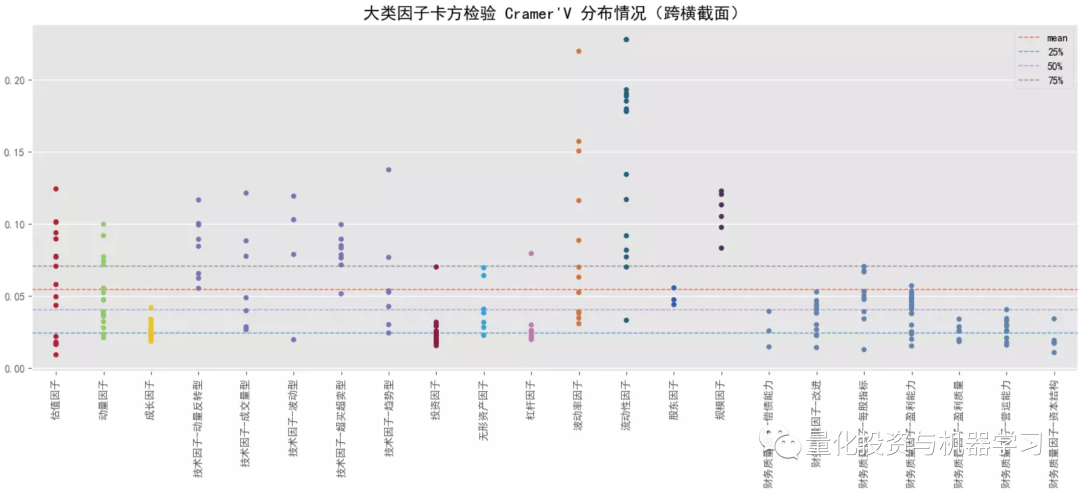
下图测试，因子 x 离散化采用方式②，阈值取0.1，收益 y 离散化采用方式①，阈值取 3，更多的是测试因子极端值的表现；对比大类因子的平均 Cramer'V 统计量情况，排名靠前的有：规模因子>流动性因子>来自量价的技术因子、波动率因子、动量因子等，量价因子普遍优于基本面因子，与前面 F 统计量的 p 值占比相对一致；结合卡方检验的 p 值显著性占比情况，与 Cramer'V 统计量的排名也是保持一致的。对比跨横截面的结果，所有大类因子在跨横截面后 Cramer'V 值都有所降低，但显著时间点占比有所提高，这可能是受样本量的影响。对比 F 统计量，Cramer'V 给出的结果更一致，更稳定，而且还能捕捉非线性关系。
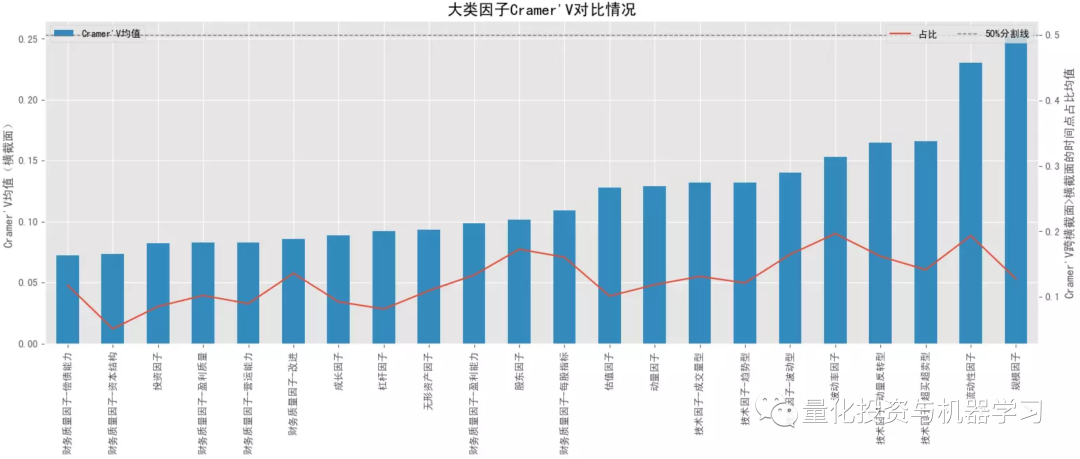
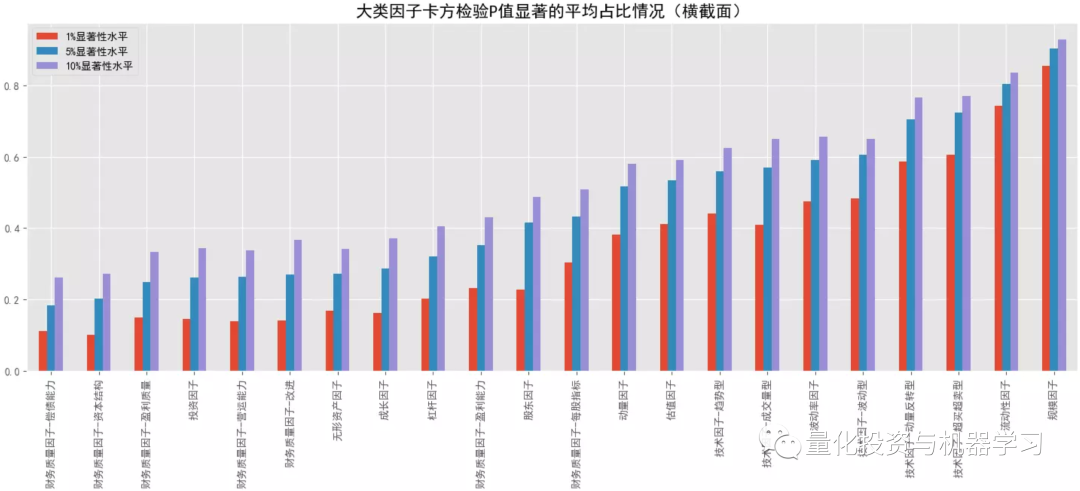
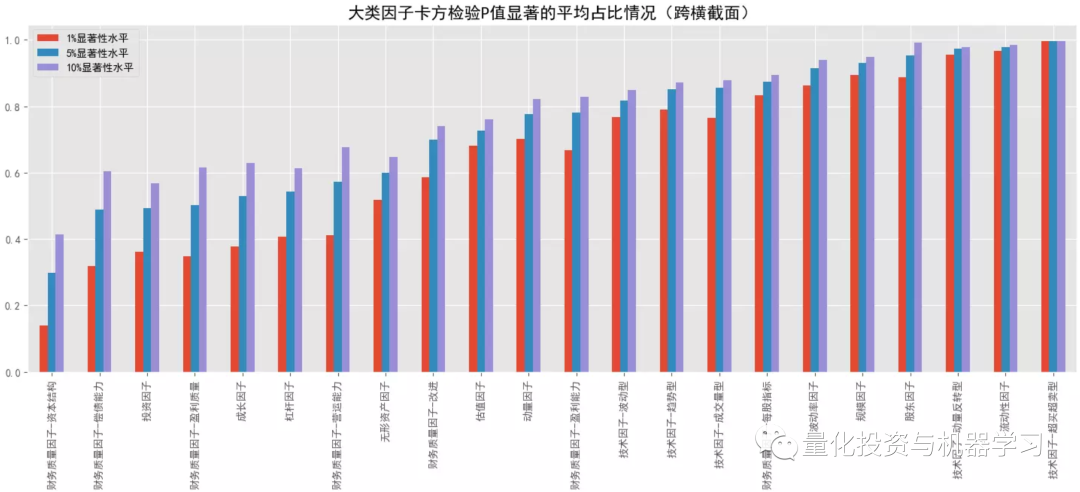
结合下面几幅图可知各大类因子中 Cramer'V 统计量排名最靠前和排名最靠后的具体因子以及它们在分布图中的大致位置（最顶端的点和最底端的点）。排名靠前因子中，量价因子居多，排名靠后因子中，基本面因子居多。
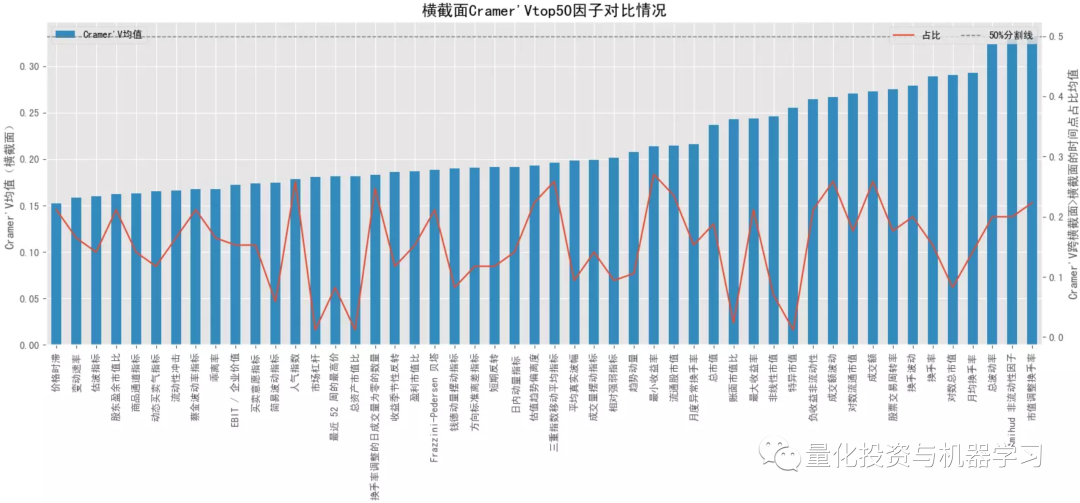
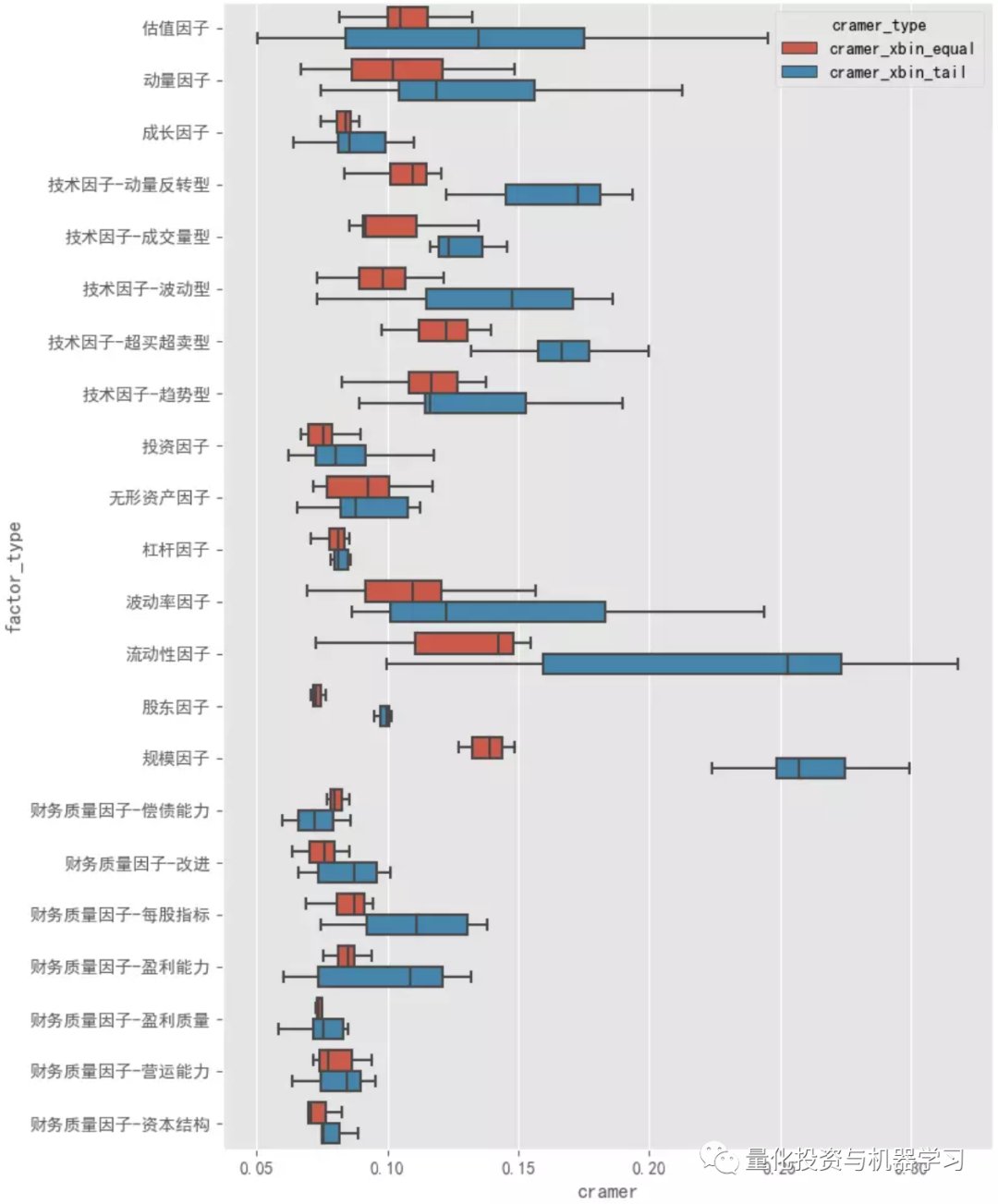
下图还进一步对比了因子 x 的 2 种离散化方式下大类因子 Cramer'V 均值分布情况（因子 x 采用 3 等均分 equal 和保留 10% 的尾部 tail，收益 y 同上，采用 3 等均分），极端值下因子与收益的关联关系相对更高，这个现象在财务质量因子上的表现相对要弱些。
互信息
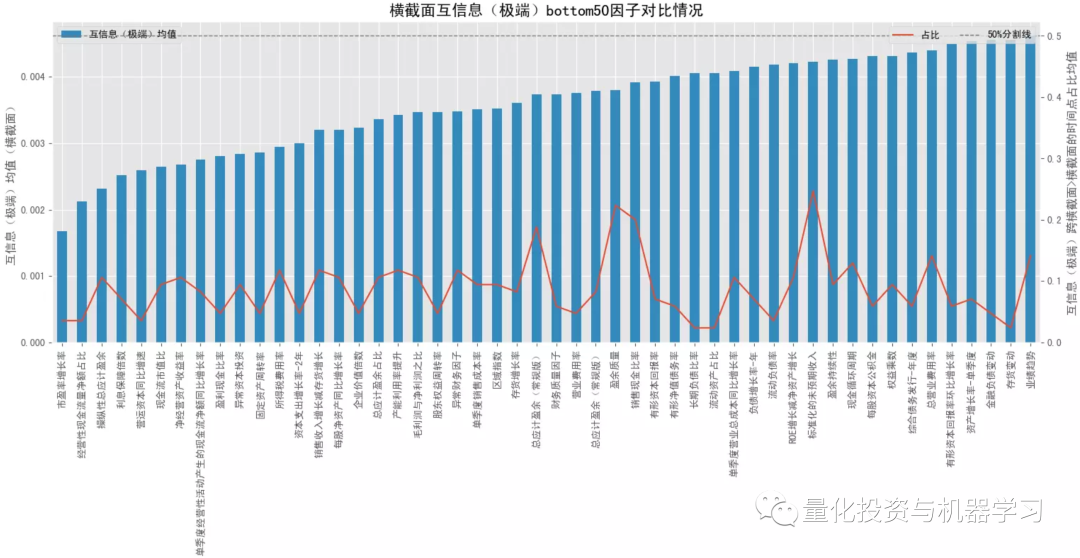
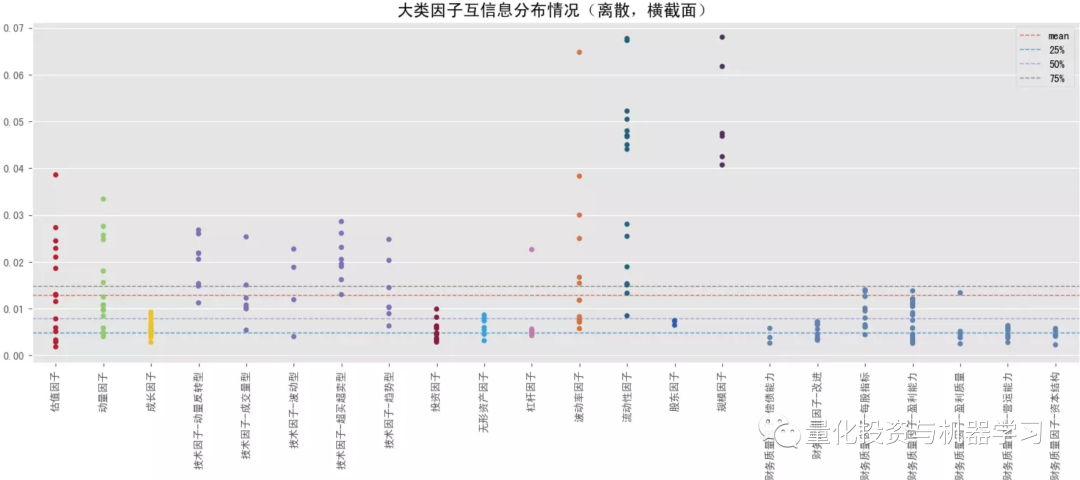
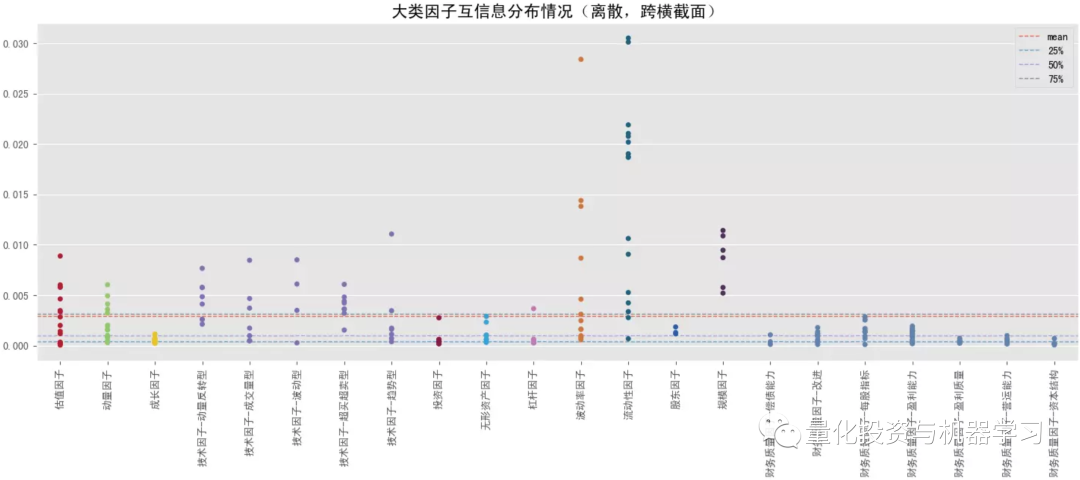
互信息是从信息熵的角度考察变量间的关系，即收益 y 在给定因子 x 信息的情况下减少的不确定性，互信息越高，因子 x 带来的关于收益 y 的信息越多，越有助于减少收益 y 的不确定性，收益 y 对因子 x 的依赖程性也越高，也能捕捉变量间的非线性关系。决策树中用于判断分支节点的信息增益（公式2）本质上和互信息（公式1）是一致的。sklearn 在特征选择模块中提供了 2 中计算互信息的方法，mutual_info_classif （即mutual_info_score）适用于离散目标变量，mutual_info_regression 适用于连续目标变量。 下图测试结果调用 mutual_info_regression 计算互信息，大类因子中，互信息排名靠前的有：流动性因子>规模因子>来自量价的技术因子、波动率因子、动量因子等，也是量价因子表现优于基本面因子，跨横截面后互信息也都有所降低，整体上与卡方检验的结果较为一致。结合下面几幅图可知各大类因子中互信息排名最靠前和排名最靠后的具体因子以及它们在分布图中的大致位置（最顶端的点和最底端的点）。排名靠前因子中，量价因子居多，比如 Amihud 非流动性因子、总波动率因子、各类换手率因子等；排名靠后因子中，基本面因子居多，如各类财务质量因子。 下图测试结果调用 mutual_info_score 计算互信息，在测试前对因子和收益做了离散化操作（因子 x 离散化采用方式 ②，阈值取0.1，收益 y 离散化采用方式 ①，阈值取 3），重点评价极端值的表现。大类因子排序有些许变化，但整体上也是呈现“量价因子表现优于基本面因子，跨横截面后互信息也都有所降低”的规律。对比连续值下的互信息，极端值下互信息头尾差异较大，规模因子、流动性因子极端值的作用比基本面因子高很多。 极端值下，互信息最高的是市值调整的换手率，其次是 Amihud 非流动性因子，然后是一些规模因子，规模因子极端值的作用整体上要强于流动性因子。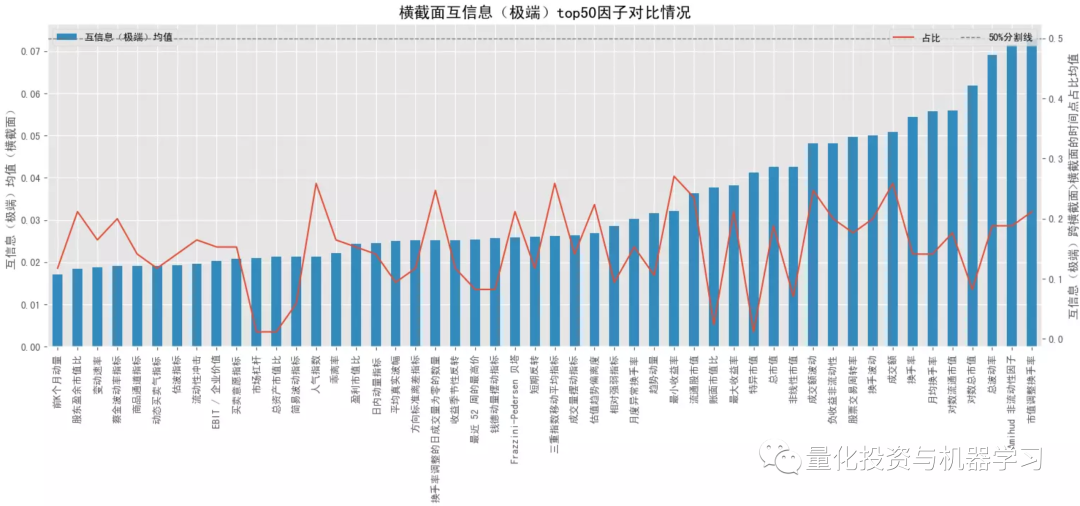
def discretization_processing(x, y, x_bin=0.1, y_bin=3) -> tuple:
'''
x_bin: int -> use all cases and split equally; 0 use tails only and get two bins; None -> raw x
y_bin: int -> split equally; 'zero' -> split at zero and get only two bins (win and lose), y=0 belong to win; None -> raw y
return：tuple (discretized feature, discretized target)
'''
# cut target y
if isinstance(y_bin, int):
y = pd.qcut(y, q=y_bin, duplicates='drop')
elif y_bin=='zero':
y = np.where(y>=0, 1, 0)
elif y_bin is None:
y = y
else:
raise ValueError("y_bin must be int or 'zero' or None !")
# cut predictor x
if isinstance(x_bin, float) & (x_bin<=0.5) & (x_bin>0):
x_bin_ = int(1/x_bin)
x = pd.qcut(x, q=x_bin_, duplicates='drop')
elif isinstance(x_bin, int):
x = pd.qcut(x, q=x_bin, duplicates='drop')
elif x_bin is None:
x = x
else:
raise ValueError("x_bin must be fraction in (0,0.5] or int or None !")
# only get tail
if isinstance(x_bin, float):
un = np.unique(x)
id = np.where((x==un[0])|(x==un[-1]))[0]
x = x[id]
y = y[id]
return (x,y)
总结
本文对因子日历计算了多个可用于因子筛选的评价指标。但总体上，因子筛选的指标要与模型的选择保持一致，具体来说：1、如果是线性的因子模型，那么因子评价的指标只需要能够评估因子与收益率之间的线性关系即可，如 IC 或 Rank IC；2、如果是机器学习的非线性模型，那么因子评价的指标不仅要能反映因子与收益的线性关系还要反映非线性关系，如 Chi-square 及 Carmer's V 等。后面我们会将本文介绍的因子筛选指标与机器学习模型结合使用，测试因子筛选对模型效果的提升作用。
