之前介绍了方差是用来刻画数据波动性的统计量,那么协方差就是描述两个变量之间的变动关系。通俗地理解为:两个变量是同向变化?还是反向变化?同向或反向程度有多少?
X变大,Y也变大,说明两个变量是同向变化的,这时协方差就是正的。X变大,Y变小,说明两个变量是反向变化的,这时协方差就是负的。并且从数值大小来看,协方差的绝对值越大,则两个变量同向或反向的程度也越大,即有较强的相关。
公式的计算很简单,每个X与其均值之差乘以Y与其均值之差得到一个乘积,再将其都加起来求个均值即可。比如有两个变量X,Y,观察7个样本,画出他们的变化情况,并且很明显是同向变化的。
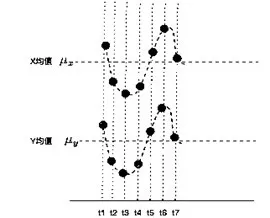
可以发现每一时刻的值与的值的正负号相同(比如t1时刻,他们同为正,t2时刻他们同为负):
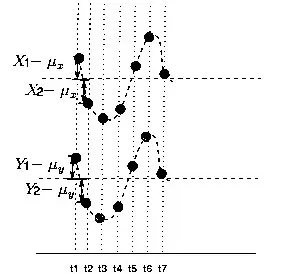
于是当他们同向变化时,的值与的值乘积为正。这样,当你把7个时刻的乘积加在一起,求平均后也就是正数了。如果反向运动:
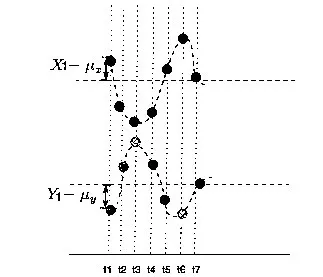
很明显,的值与的值的正负号相反,于是其乘积就是负值,计算出来的协方差也就是负数了。上面说的两种情况比较特殊,很多时候XY两个变量的变动没有规律,比如:

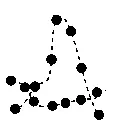
这种情况下某些的值与的值乘积为正,某些的值与的值乘积为负。加在一起后,其中的一些正负项就会抵消掉,最后平均得出的值就是协方差,通过协方差的数值大小,就可以判断这两个变量同向或反向的程度了。所以,在7个样本中,与的乘积为正的越多,说明同向变化的次数越多,亦即同向程度越高,反之亦然。总而言之,
若协方差为正,则X和Y同向变化;反之协方差为负,则反向变化;协方差绝对值越大表示同向或反向的程度越深。
其实方差也是一种特殊的协方差,只不过是X和X之间的协方差。
Part2 相关系数
相关系数的公式为:其实就是用X、Y的协方差除以X和Y的标准差。所以相关系数可以看成剔除了两个变量单位的影响、标准化后的特殊协方差。它可以反映两个变量变化是同向还是反向的,同向为正,反向为负。并且它又是标准化后的协方差,则它出现最重要的目的来了,就是消除两个变量单位的影响,使得不同变量的相关系数之间具有可比性。比如下面两种情况,关注一下纵轴的刻度:
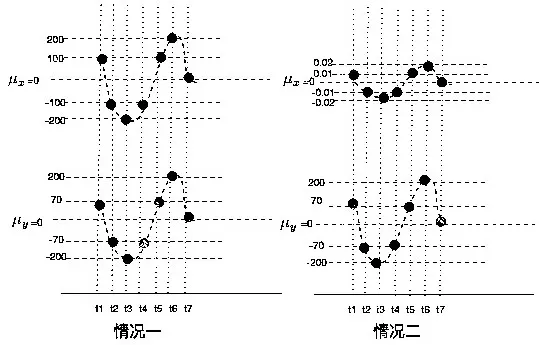
很容易可以看出两种情况下X和Y都是同向变化的,并且它们变化的方式都大致相同,在特定的样本点同为正或同为负,那么它们理应具有相同的相关关系。于是可以计算一下他们的协方差:
第一种情况下:[(100-0)×(70-0)+(-100-0)×(-70-0)+(-200-0)×(-200-0)…]÷7≈15428.57
第二种情况下:[(0.01-0)×(70-0)+(-0.01-0)×(-70-0)+(-0.02-0)×(-200-0)…]÷7≈1.542857
协方差差了一万倍,只能看出两种情况都是正相关的,但是我们能说第一种情况就相关性更强吗?在上面两种情况中,虽然X和Y的变化方向都相同,但是每次变化的幅度不相同,主要原因是单位的不一致引起的。所以,为了能准确比较两个变量的相关程度,我们就要把变化幅度对协方差的影响中剔除掉,也就是要去掉单位的影响,于是就要使用相关系数。那么如何剔除变量变化幅度的影响呢?很自然的就应该使用前面提到的方差和标准差了!相关系数是协方差除以标准差,当X或Y的波动变大的时候,它们的协方差会变大,标准差也会变大,这样相关系数的分子分母都变大,相互抵消,变小时也亦然。于是相关系数不像协方差一样可以在实数域上取值,它只能在+1到-1之间变化,具体为什么是+1和-1,可以自行Google柯西-斯瓦茨不等式。总之,对于两个变量X、Y,
当他们的相关系数为1时,说明两个变量线性相关程度最大,两个变量存在线性关系。随着相关系数减小,两个变量相关程度也变小。当相关系数为0时,两个变量的线性无关,但要注意,无关不一定独立。当相关系数继续变小,小于0时,两个变量开始出现反向相关。当相关系数为-1时,说明两个变量线性相关程度也最强,不过是相反的线性相关,反相变化。
让我们再回到前面X和Y的例子,用相关系数来衡量相关程度:
第一种情况:
X的标准差为
Y的标准差为
于是相关系数为
说明第一种情况下,X和Y有极强的相关性,几乎是线性相关。
第二种情况:
X的标准差为
Y的标准差为
于是相关系数为
在第二种情况下,X的标准差较第一种小了10000倍,即变化幅度小了,但是并不改变X和Y线性高度相关的事实。两种情况的相关系数相等,X和Y具有相同的相关性,故而使用相关系数来衡量和比较相关性,要比协方差合适很多。在第二种情况下,X的标准差较第一种小了10000倍,即变化幅度小了,但是并不改变X和Y线性高度相关的事实。
两种情况的相关系数相等,X和Y具有相同的相关性,故而使用相关系数来衡量和比较相关性,要比协方差合适很多。
机器学习交流qq群772479961,加入微信群请扫码