2024年8月8日,Nat. Comput. Sci.在线发表了复旦大学向红军教授和杨吉辉青年研究员课题组的研究论文,题目为《Accelerating the calculation of electron–phonon coupling strength with machine learning》,论文的第一作者为Yang Zhong和Shixu Liu。
电子-声子耦合(EPC)在各种物理现象中至关重要,如温度依赖的带隙、非辐射载流子复合、热导率和电导率以及超导性。在半导体中,EPC通常主导载流子散射,限制载流子迁移率。在Bardeen-Cooper-Schrieffer(BCS)超导体中,EPC诱导电子之间的吸引相互作用,形成库珀对并实现超导性。因此,准确计算EPC对于理解材料中的电子和声子行为至关重要。目前,密度泛函微扰理论(DFPT)结合最大化局域Wannier函数是计算布里渊区密集电子和声子波矢网格上EPC矩阵元的最有效方法。
粗网格上DFPT计算的微扰势也可以转换为局域原子轨道(AO)基集中的EPC矩阵,提供与Wannier插值方法类似的精度。然而,DFPT的计算成本与原子数(N)成比例,即O(N3),这限制了它在大型体系中的应用。此外,DFPT目前仅支持局域或半局域密度泛函,这不足以准确表征许多电子性质,如半导体带隙。精确的EPC预测需要先进的泛函,如Heyd-Scuseria-Ernzerhof(HSE)杂化泛函,但由于自洽密度泛函理论(DFT)中的高计算要求,使用杂化泛函或GW(其中G表示单粒子格林函数,W表示屏蔽库仑相互作用)微扰理论计算全布里渊区的EPC具有挑战性。
这将EPC研究限制在小型体系中,并将精度限制在标准交换关联泛函上。最近,已经提出了投影缀加波(PAW)方法中的实空间有限差分方案,用于具有HSE泛函的EPC计算。然而,HSE泛函所需的超胞计算仍然非常昂贵。此外,基于奇异值分解(SVD)方法压缩了所需的EPC矩阵元,但仍然依赖于粗网格上计算成本高的DFPT计算。为了探索实际材料中与EPC相关的特性,需要DFT以外的方法来使用先进的泛函进行高效准确的EPC计算。
在此研究中,作者开发了一种机器学习方法,使用E(3)-等变哈密顿图神经网络(HamGNN)来加速EPC计算。通过有效计算哈密顿量及其梯度,该方法将EPC计算速度提高了几个数量级,使其适用于非常密集网格上的大型体系。通过对HSE数据的训练,该方法可以有效地计算具有HSE先进泛函的EPC。通过使用HSE泛函准确预测GaAs的载流子迁移率和大型kagome晶体CsV3Sb5的超导性来证明其能力。
研究结果表明,HSE泛函对于正确捕获GaAs的电子结构和输运性质至关重要,而标准DFT泛函低估了有效电子质量,高估了载流子迁移率。对于CsV3Sb5,成功地在其压力诱导超导相图中再现了双圆顶。此外,通过计算CsV
3Sb5 2×2×1电荷密度波(CDW)超晶格中的EPC,预测了一个接近实验观测值的超导转变温度(Tc)。这项研究中的机器学习框架为精确计算EPC提供了一种超越DFT的有效方法,特别是在大型体系或需要先进泛函的体系中。
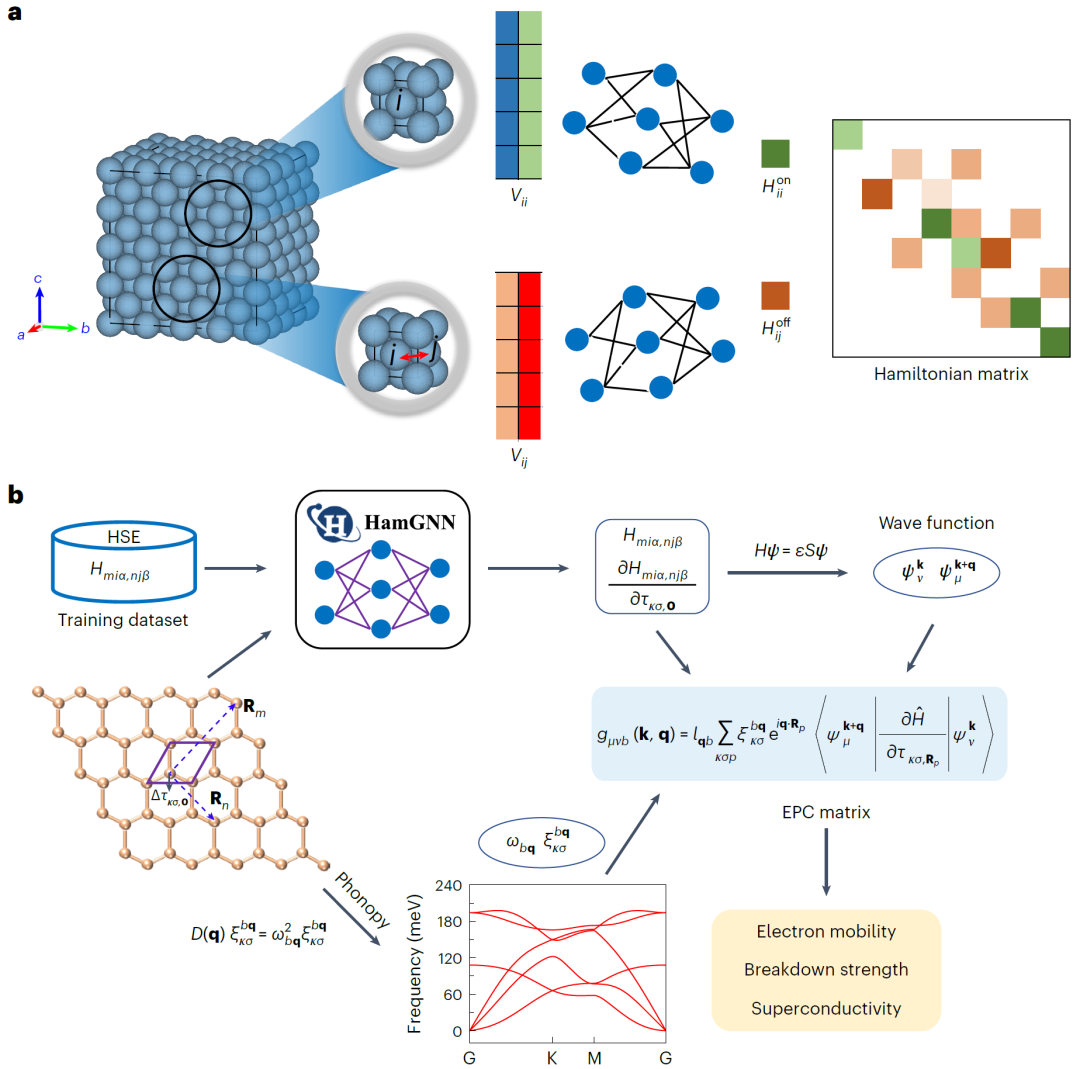
图1 利用HamGNN高效构建哈密顿矩阵和电子-声子相互作用框架
图4 CsV3Sb5的晶体结构、kagome晶格和超导转变温度
图5 CsV3Sb5 CDW相中的能带、声子谱和原子振动模式
Zhong, Y., Liu, S., Zhang, B. et al. Accelerating the calculation of electron–phonon coupling strength with machine learning. Nat. Comput. Sci., 2024.https://doi.org/10.1038/s43588-024-00668-7https://www.nature.com/articles/s43588-024-00668-7