特征机器学习特征工程和选择是将数据转化为最佳表示的艺术,以大大提升机器学习的效果。本指南是初学者的简明参考,提供了最简单但广泛使用的特征工程和选择技术。机器学习是让计算机在没有明确编程的情况下进行操作的学科——阿瑟·塞缪尔
机器学习是一种数据科学技术,它帮助计算机从现有数据中学习,以预测未来的行为、结果和趋势。
机器学习领域试图回答这样一个问题:“我们如何构建能够随着经验自动改进的计算机系统,以及管理所有学习过程的基本规律是什么?”-卡内基梅隆大学
从狭义上讲,在数据挖掘的背景下,机器学习(ML)是让计算机从历史数据中学习,识别数据中的模式/关系,然后进行预测的过程
将组成机器学习工作流的任务划分为多个阶段的方法有很多。但一般来说,基本步骤与上图所示类似。
特征:也称为属性/自变量/预测因子/输入变量。它是指被观察现象的个体可测量属性/特征[维基百科]。例如,一个人的年龄等。
目标:也称为因变量/响应变量/输出变量。它是监督学习中被预测的变量。
算法:用于实现特定机器学习技术的具体过程。线性回归等。
模型:应用于数据集的算法,包括其设置(其参数)。Y=4.5x+0.8等。我们希望模型能够最好地捕捉特征与目标之间的关系。
监督学习:用标记数据训练模型,以生成对新数据响应的合理预测。
无监督学习:用未标记的数据训练模型,以发现数据中的内在结构/模式。
- 强化学习:该模型是通过最大化奖励函数从一系列动作中学习而来的,可以通过惩罚不良行为和/或奖励良好行为来最大化奖励函数。自动驾驶等。
定义:所观察现象的任何可测量的属性/特征。它们被称为“变量”,因为它们所取的值在一个群体中可能会变化(而且通常会变化)。变量类型如下表:
注意:在现实中,我们可能由于各种原因而具有混合类型的变量。例如,在信用评分中,“错过付款状态”是一个常见的变量,其值可以为1、2、3,表示客户在其账户中错过了1-3次付款。如果客户在该账户上违约,它还可以取值D。我们可能必须在数据清洗的某些步骤后转换数据类型。
当存在缺失值时,某些算法无法工作
- 即使对于处理缺失数据的算法,如果不进行处理,模型也可能导致不准确的结论
了解数据集中引入缺失字段的机制非常重要。根据机制的不同,我们可以选择以不同的方式处理缺失值。这些机制最早是由Rubin提出的。如果所有观测值的缺失概率相同,则变量完全随机缺失(MCAR)。当数据MCAR时,数据缺失与数据集内任何其他观测值或缺失值之间绝对没有关系。换句话说,这些缺失数据点是数据的随机子集。没有什么系统性的因素使得某些数据比其他数据更容易缺失。如果随机缺失观察值,那么忽略这些情况不会影响所做的推断。当缺失值的倾向与观察到的数据之间存在系统关系时,就会发生随机缺失(MAR)。换句话说,观测值缺失的概率仅取决于可用信息(数据集中的其他变量),而不取决于变量本身。例如,如果男性比女性更有可能透露自己的体重,那么体重就是MAR(可变性别)。对于那些决定不透露体重的男性和女性,体重信息将随机缺失,但由于男性更容易透露体重,女性的缺失值将比男性更多。在上述情况下,如果我们决定继续使用缺失值的变量,我们可能会从包含性别中受益,以控制缺失观测值的权重偏差。缺失取决于尚未记录的信息,而这些信息也预测了缺失值。例如,如果某种治疗引起不适,患者更有可能退出研究(而“不适”未被测量)。在这种情况下,如果我们删除那些缺失的案例,数据样本就会产生偏差缺失取决于(潜在缺失的)变量本身。例如,收入较高的人不太可能透露这些信息。但是我们应该牢记,我们很难百分之百确定数据是MCAR、MAR还是MNAR,因为未观察到的预测变量(潜变量)是未被观察到的。
在实际场景中,当我们很难确定缺失值的机制,或者没有足够的时间对每个缺失变量进行深入研究时,一种流行的方法是采用以下策略:均值/中位数/众数插补(取决于分布情况)
分布末端插补
同时,这样我们既能捕捉到缺失值,又能获得完整的数据集。注意:一些算法(如XGboost)将缺失数据处理纳入了其模型构建过程,因此无需执行此步骤。但是,确保您了解算法如何处理它们并向业务团队解释这一点非常重要。定义:异常值是指与其他观测值偏差很大,以至于引起怀疑它是由不同机制生成的观测值。注意:根据具体情况,异常值要么值得特别关注,要么应该完全忽略。例如,信用卡上的异常交易通常是欺诈活动的迹象,而一个人的身高为1600cm很可能是由于测量误差造成的,应该被过滤掉或用其他东西代替。一些算法对异常值非常敏感,例如,Adaboost可能会将异常值视为“硬”情况,并对异常值施加巨大的权重,从而产生泛化能力较差的模型。任何依赖于均值/方差的算法都对异常值敏感,因为这些统计数据受到极端值的影响很大。另一方面,一些算法对异常值更鲁棒。例如,决策树在创建树的分支时往往会忽略异常值的存在。通常,树通过询问变量x是否大于等于值t来进行分割,因此异常值将落在分支的每一侧,但无论其大小如何,它都将被视为与其他值一样对待。事实上,异常分析和异常检测是一个巨大的研究领域。Charu的书《异常分析》提供了对这个主题的深刻见解。PyOD是一个全面的Python工具包,其中包含该领域的许多高级方法。这里列出的所有方法都是针对单变量异常值检测的。多变量异常值检测超出了本指南的范围。
然而,除了这些方法,更重要的是要记住,业务背景应该支配你如何定义和应对这些异常值。你的发现的意义应该由潜在的背景决定,而不是数字本身。
处理数据中的异常值有很多策略,并且根据上下文和数据集的不同,任何策略都可能是正确或错误的方法。在做出决定之前,了解异常值的性质很重要。注意:在某些情况下,罕见值(如异常值)可能包含数据集的有价值信息,因此需要特别注意。例如,交易中的罕见值可能表示欺诈。分类变量中的罕见值往往会导致过拟合,特别是在基于树的方法中。
大量不常用的标签增加了噪声,信息很少,因此导致过拟合。
稀有标签可能出现在训练集中,但不会出现在测试集中,因此导致对训练集的过度拟合。
- 测试集中可能会出现罕见的标签,而训练集中则不会出现。因此,模型将不知道如何对其进行评估。

- 当变量中有一个主要类别(超过 90%)时:观察该变量与目标之间的关系,然后要么丢弃该变量,要么保持原样。在这种情况下,变量通常对预测没有用,因为它几乎是恒定的(我们稍后将在特征选择部分看到)。
- 当类别数量很少时:保持原样。因为只有少数类别不太可能带来如此多的噪音。
- 当高基数时:尝试上述两种方法。但这并不能保证比原始变量更好的结果。
定义:分类变量中标签的数量被称为基数(cardinality)。变量中标签数量多被称为高基数(high cardinality)。具有太多标签的变量往往比只有少数标签的变量占主导地位,特别是在基于树的算法中。
变量中的大量标签可能会引入噪声,即使有信息,也很少,因此使机器学习模型易于过拟合。
一些标签可能只存在于训练数据集中,而不存在于测试数据集中,因此导致算法过度拟合训练集。
- 相反,测试集中可能会出现训练集中没有出现的新标签,因此算法无法对新观察值进行计算。

所有这些方法都试图对一些标签进行分组并降低基数。用决策树对标签进行分组等同于4.2.2节中介绍的“使用决策树进行离散化”方法,该方法旨在将标签合并为更加同质的组。将罕见出现的标签归为同一类别等同于3.3.2节中介绍的方法。定义:特征缩放是一种用于标准化数据自变量或特征范围的方法。在数据处理中,它也被称为数据归一化,通常在数据预处理步骤中执行。如果输入范围发生变化,在某些算法中,目标函数将无法正常工作。梯度下降在完成特征缩放后收敛得更快。梯度下降是一种常用的优化算法,用于逻辑回归、支持向量机、神经网络等。涉及距离计算的算法,如KNN、聚类,也受到特征大小的影响。只需考虑欧几里德距离的计算方法:取观测值之间平方差之和的平方根。这种距离会受到变量之间尺度差异的极大影响。方差较大的变量对这种度量的影响比方差较小的变量大。注意:基于树的算法几乎是唯一不受输入量影响的算法,因为我们可以很容易地从树的构建方式中看出。在决定如何进行分割时,树算法会寻找诸如“特征值X是否大于3.0”之类的决策,并在分割后计算子节点的纯度,因此特征的规模并不重要。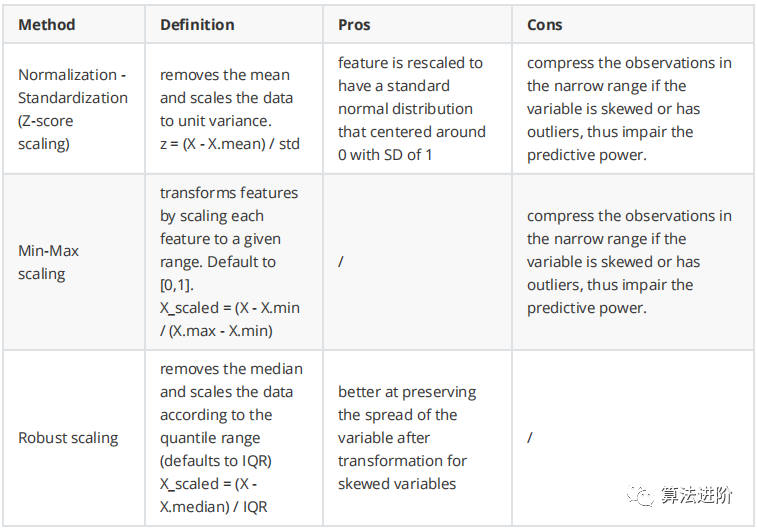
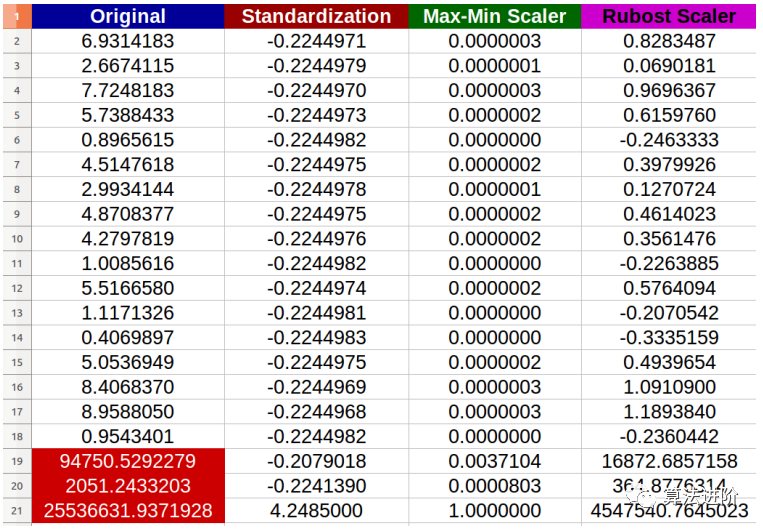
正如我们所看到的,归一化-标准化和最小-最大方法会将大多数数据压缩到一个较窄的范围,而鲁棒缩放器在保持数据分布方面做得更好,尽管它不能从处理结果中删除异常值。记住删除/输入异常值是数据清理中的另一个主题,应该提前完成。如果你的特征不是高斯分布,比如,具有偏斜分布或异常值,那么归一化-标准化不是一个好的选择,因为它会将大多数数据压缩到一个狭窄的范围。
然而,我们可以将特征转换为高斯分布,然后使用归一化 - 标准化。特征转换将在第3.4节中讨论。
在进行距离或协方差计算(如聚类、PCA和LDA等算法)时,最好使用归一化-标准化,因为它会消除尺度对方差和协方差的影响。
- Min-Max缩放与Normalization-Standardization具有相同的缺点,并且新数据可能不会限制在[0,1],因为它们可能超出原始范围。一些算法,例如一些深度学习网络,更喜欢在0-1范围内输入,因此这是一个不错的选择。
定义:离散化是通过创建一组跨越变量值范围的连续区间,将连续变量转换为离散变量的过程。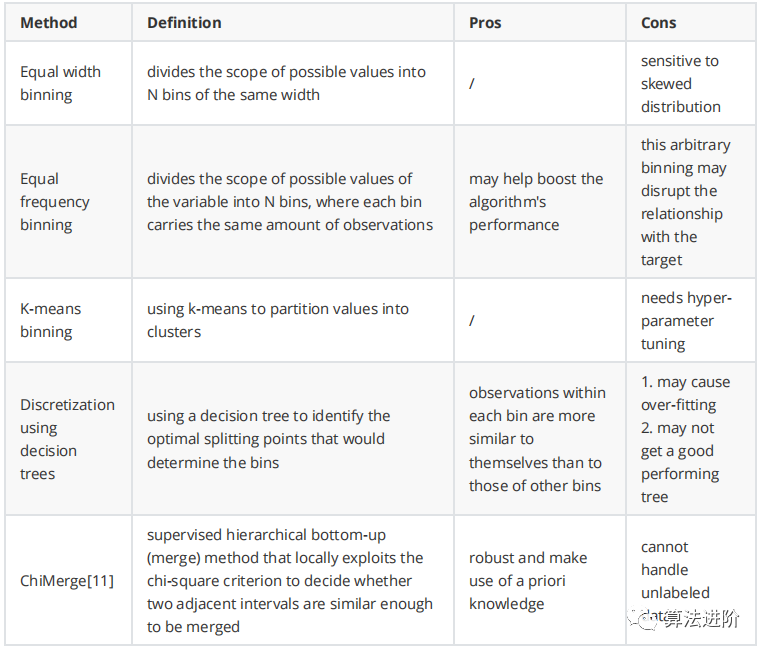
一般来说,没有最好的离散化方法。这确实取决于数据集和后续的学习算法。在决定之前,仔细研究你的特性和上下文。你也可以尝试不同的方法并比较模型的性能。
我们必须将分类变量的字符串转换为数字,以便算法能够处理这些值。即使你看到一个算法可以接受分类输入,最有可能的是,该算法将编码过程纳入其中。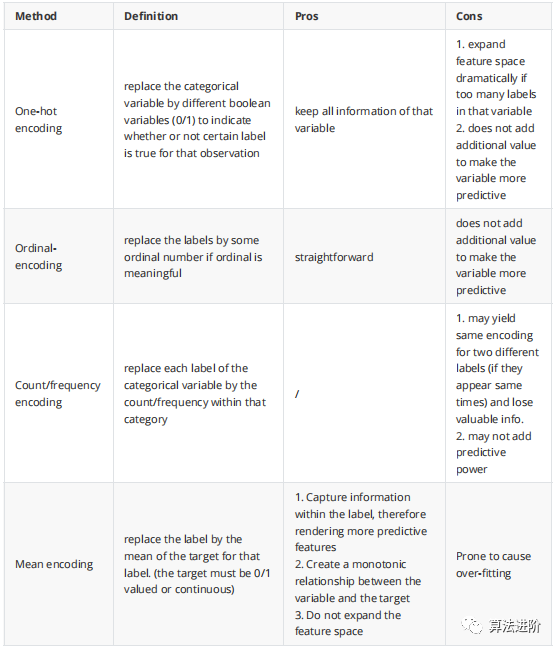
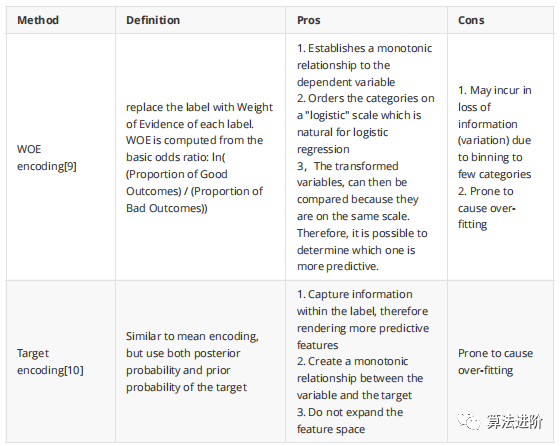
注意:如果我们在线性回归中使用one-hot编码,我们应该保留k-1个二进制变量以避免多重共线性。这对于在训练期间同时查看所有特征的任何算法都是如此。包括SVM、神经网络和聚类。另一方面,基于树的算法需要整个二进制变量集来选择最佳分割。注意:不建议在树算法中使用one-hot编码。one-hot将导致分裂高度不平衡(因为原始分类特征的每个标签现在都是一个新特征),结果导致两个子节点中的任何一个都不会有很好的纯度增益。由于one-hot特征被分解为许多部分,因此one-hot特征的预测能力将弱于原始特征。线性回归是一种直接的方法,用于预测定量响应Y,基于不同的预测变量X1、X2、... Xn。它假设X(s)和Y之间存在线性关系。从数学上讲,我们可以将这种线性关系写成Y≈β0+β1X1+β2X2+…+βnXn。同样,对于分类,逻辑回归假设变量与对数机率之间存在线性关系。对数(概率)=β0 + β1X1 + β2X2 + ... + βnXn如果机器学习模型假设预测值Xs和结果Y之间存在线性关系,当不存在这种线性关系时,模型的表现会较差。在这种情况下,我们最好尝试另一种不作这种假设的机器学习模型。如果没有线性关系,我们必须使用线性/逻辑回归模型,数学变换/离散化可能有助于建立关系,尽管它不能保证更好的结果。与结果Y之间存在线性关系
多元正态性
无或很少多重共线性
同方差性,也称为方差齐性,描述了一种情况,即误差项(即独立变量(Xs)和因变量(Y)之间的关系中的“噪声”或随机干扰)在所有独立变量的值中都是相同的。违反同方差性和/或正态性的假设(假设数据分布是同方差或高斯的,而实际上不是)可能会导致模型性能不佳。其余的机器学习模型,包括神经网络、支持向量机、基于树的方法和PCA,对自变量的分布没有任何假设。然而,在许多情况下,模型性能可能会受益于“类高斯”分布。为什么模型可以从“高斯型”分布中受益?在正态分布的变量中,可用于预测Y的X观测值在更大的值范围内变化,即X的值在更大的范围内“扩散”。在上述情况下,对原始变量的转换可以帮助使变量更接近高斯分布的钟形。
对数变换在应用于偏斜分布时非常有用,因为它们往往会扩大落在较低幅度范围内的值,并倾向于压缩或减少落在较高幅度范围内的值,这有助于使偏斜分布尽可能地接近正态分布。sklearn中的Box-Cox变换是另一种属于幂变换函数家族的流行函数。该函数有一个先决条件,即要转换的数值必须是正数(类似于对数变换所期望的)。如果它们是负数,则使用常数值进行移位会有所帮助。从数学上讲,Box-Cox变换函数可以表示如下。sklearn中的分位数变换将特征转换为遵循均匀分布或正态分布。因此,对于给定的特征,这种变换往往会分散最常见的值。它还降低了(边际)异常值的影响:因此,这是一种稳健的预处理方案。然而,这种变换是非线性的。它可能会扭曲以相同尺度测量的变量之间的线性相关性,但会使以不同尺度测量的变量更直接地具有可比性。我们可以用QQ图来检查变量在转换后是否呈正态分布(理论分位数上值的45度直线)。下面是一个例子,展示了sklearn的箱线图/Yeo-johnson/分位数变换的效果,将各种分布的数据映射到正态分布。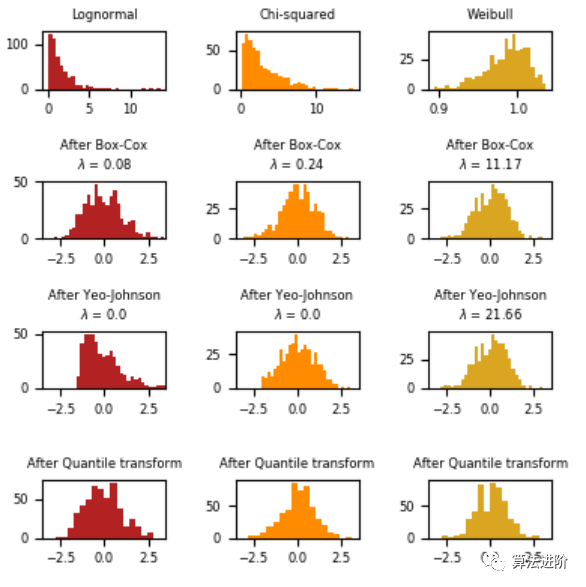
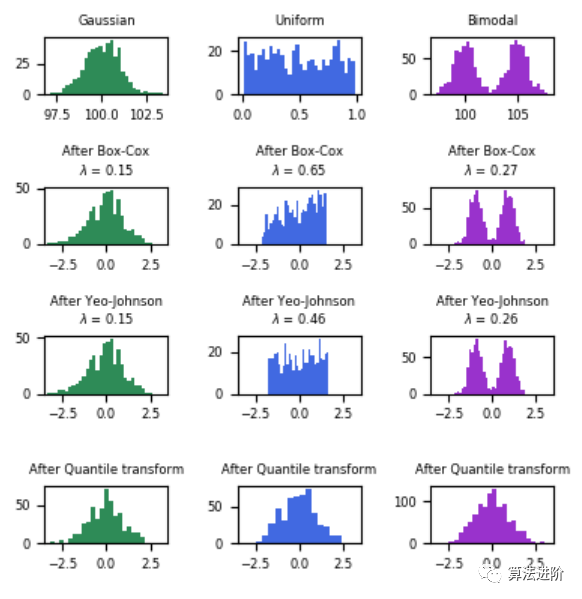
在“小”数据集(少于几百个点)上,分位数转换器很容易过度拟合。建议使用幂变换。定义:通过现有功能的组合创建新功能。这是向数据集添加领域知识的好方法。如第3.1节所述,我们可以创建一个新的二进制特征,用0/1表示原始特征上的观察值是否有缺失值通过对原始特征进行简单的统计计算来创建新特征,包括:
以通话记录为例,我们可以创建新的功能,如通话次数、呼入/呼出次数、平均通话时长、每月平均通话时长、最长通话时长等。在获得一些简单的统计衍生特征后,我们可以将它们交叉在一起。用于交叉的常见维度包括:还是以通话记录为例,我们可以拥有交叉特征,如:夜间/日间通话次数、不同业务类型(银行/出租车服务/旅行/酒店)下的通话次数、过去3个月的通话次数等。第4.5.2节中提到的许多统计计算可以再次用于创建更多特征。注意:可以在此处找到一个名为Featuretools的开源python框架,它可以帮助自动生成这些特征。常见技术。例如,为了预测一个分支机构信用卡销售的未来表现,信用卡销售/销售人员或信用卡销售/营销支出等比率将比仅使用分支机构销售的绝对卡数更有说服力。考虑一个类别特征 A,有两个可能的值 {A1, A2}。假设 B 是一个具有可能性 {B1, B2} 的特征。那么,A 和 B 之间的特征交叉将采用以下值之一:{(A1, B1), (A1, B2), (A2, B1), (A2, B2)}。你基本上可以给这些“组合”任何你喜欢的名字。只要记住,每个组合都表示 A 和 B 的相应值所包含的信息之间的协同作用。这是一种非常有用的技术,当某些特征共同表示一个属性时,比单独表示更好。从数学上讲,你正在对分类特征的所有可能值进行叉积。这个概念类似于第3.5.3节的特征交叉,但这个概念特别指的是两个分类特征之间的交叉。叉积也可以应用于数值特征,从而在A和B之间产生新的交互特征。这可以通过sklearn的多项式特征轻松实现,它生成一个新的特征集,由所有特征的多项式组合组成,其次数小于或等于指定的次数。例如,三个原始特征{X1,X2,X3}可以生成一个特征集{1,X1X2,X1X3,X2X3,在基于树的算法中,每个样本将被分配到一个特定的叶子节点。每个节点的决策路径可以被视为一个新的非线性特征,我们可以创建N个新的二元特征,其中n等于树或树集合中的叶子节点总数。然后,这些特征可以被馈送到其他算法,如逻辑回归。这种方法的好处是我们可以将几个特征的复杂组合组合在一起,这很有意义(正如树的学习算法所构造的那样)。与手动进行特征交叉相比,这为我们节省了大量时间,并且广泛用于在线广告行业的点击率(CTR)。从以上内容中我们可以看出,人工生成特征需要付出大量努力,并且可能无法保证良好的回报,特别是在我们拥有大量特征的情况下。使用树进行特征学习可以被视为自动创建特征的早期尝试,随着深度学习方法在2016年左右流行起来,它们也在这一领域取得了一些成功,如自动编码器和受限玻尔兹曼机。它们已被证明可以自动并以无监督或半监督的方式学习特征的抽象表示(压缩形式),这反过来又支持了语音识别、图像分类、物体识别等领域最先进的结果。然而,这些特征的可解释性有限,深度学习需要更多的数据才能提取高质量的结果。
mean(): Compute mean of groupssum(): Compute sum of group valuessize(): Compute group sizescount(): Compute count of groupstd(): Standard deviation of groupsvar(): Compute variance of groupssem(): Standard error of the mean of groupsfirst(): Compute first of group valueslast(): Compute last of group valuesnth() : Take nth value, or a subset if n is a listmin(): Compute min of group valuesmax(): Compute max of group valuesdef median(x): return np.median(x)
def variation_coefficient(x): mean = np.mean(x) if mean != 0: return np.std(x) / mean else: return np.nan
def variance(x): return np.var(x)
def skewness(x): if not isinstance(x, pd.Series): x = pd.Series(x) return pd.Series.skew(x)
def kurtosis(x): if not isinstance(x, pd.Series):
x = pd.Series(x) return pd.Series.kurtosis(x)
def standard_deviation(x): return np.std(x)
def large_standard_deviation(x): if (np.max(x)-np.min(x)) == 0: return np.nan else: return np.std(x)/(np.max(x)-np.min(x))
def variation_coefficient(x): mean = np.mean(x) if mean != 0: return np.std(x) / mean else: return np.nan
def variance_std_ratio(x): y = np.var(x) if y != 0: return y/np.sqrt(y) else: return np.nan
def ratio_beyond_r_sigma(x, r): if x.size == 0: return np.nan else: return np.sum(np.abs(x - np.mean(x)) > r * np.asarray(np.std(x))) / x.size
def range_ratio(x): mean_median_difference = np.abs(np.mean(x) - np.median(x)) max_min_difference = np.max(x) - np.min(x) if max_min_difference == 0: return np.nan else: return mean_median_difference / max_min_difference def has_duplicate_max(x): return np.sum(x == np.max(x)) >= 2
def has_duplicate_min(x): return np.sum(x == np.min(x)) >= 2
def has_duplicate(x): return x.size != np.unique(x).size
def count_duplicate_max(x): return np.sum(x == np.max(x))
def count_duplicate_min(x): return np.sum(x == np.min(x))
def count_duplicate(x): return x.size - np.unique(x).size
def sum_values(x): if len(x) == 0: return 0 return np.sum(x)
def log_return(list_stock_prices): return np.log(list_stock_prices).diff()
def realized_volatility(series): return np.sqrt(np.sum(series**2))
def realized_abs_skew(series): return
np.power(np.abs(np.sum(series**3)),1/3)
def realized_skew(series): return np.sign(np.sum(series**3))*np.power(np.abs(np.sum(series**3)),1/3)
def realized_vol_skew(series): return np.power(np.abs(np.sum(series**6)),1/6)
def realized_quarticity(series): return np.power(np.sum(series**4),1/4)
def count_unique(series): return len(np.unique(series))
def count(series): return series.size
def maximum_drawdown(series): series = np.asarray(series) if len(series)<2: return 0 k = series[np.argmax(np.maximum.accumulate(series) - series)] i = np.argmax(np.maximum.accumulate(series) - series) if len(series[:i])<1: return np.NaN else: j = np.max(series[:i]) return j-k
def maximum_drawup(series): series = np.asarray(series) if len(series)<2: return 0
series = - series k = series[np.argmax(np.maximum.accumulate(series) - series)] i = np.argmax(np.maximum.accumulate(series) - series) if len(series[:i])<1: return np.NaN else: j = np.max(series[:i]) return j-k
def drawdown_duration(series): series = np.asarray(series) if len(series)<2: return 0
k = np.argmax(np.maximum.accumulate(series) - series) i = np.argmax(np.maximum.accumulate(series) - series) if len(series[:i]) == 0: j=k else: j = np.argmax(series[:i]) return k-j
def drawup_duration(series): series = np.asarray(series) if len(series)<2: return 0
series=-series k = np.argmax(np.maximum.accumulate(series) - series) i = np.argmax(np.maximum.accumulate(series) - series) if len(series[:i]) == 0: j=k else: j = np.argmax(series[:i]) return k-j
def max_over_min(series): if len(series)<2: return 0 if np.min(series) ==
0: return np.nan return np.max(series)/np.min(series)
def mean_n_absolute_max(x, number_of_maxima = 1): """ Calculates the arithmetic mean of the n absolute maximum values of the time series.""" assert ( number_of_maxima > 0 ), f" number_of_maxima={number_of_maxima} which is not greater than 1"
n_absolute_maximum_values = np.sort(np.absolute(x))[-number_of_maxima:]
return np.mean(n_absolute_maximum_values) if len(x) > number_of_maxima else np.NaN
def count_above(x, t): if len(x)==0: return np.nan else: return np.sum(x >= t) / len(x)
def count_below(x, t): if len(x)==0: return np.nan else: return np.sum(x <= t) / len(x)
def number_peaks(x, n): """ Calculates the number of peaks of at least support n in the time series x. A peak of support n is defined as a subsequence of x where a value occurs, which is bigger than its n neighbours to the left and to the right. """ x_reduced = x[n:-n]
res = None for i in range(1, n + 1): result_first = x_reduced > _roll(x, i)[n:-n]
if res is None: res = result_first else: res &= result_first
res &= x_reduced > _roll(x, -i)[n:-n] return np.sum(res)
def mean_abs_change(x): return np.mean(np.abs(np.diff(x)))
def mean_change(x): x = np.asarray(x) return (x[-1] - x[0]) / (len(x) - 1) if len(x) > 1 else np.NaN
def mean_second_derivative_central(x): x = np.asarray(x) return (x[-1] - x[-2] - x[1] + x[0]) / (2 * (len(x) - 2)) if len(x) > 2 else np.NaN
def root_mean_square(x): return np.sqrt(np.mean(np.square(x))) if len(x) > 0 else np.NaN
def absolute_sum_of_changes(x): return np.sum(np.abs(np.diff(x)))
def longest_strike_below_mean(x): if not isinstance(x, (np.ndarray, pd.Series)): x = np.asarray(x) return np.max(_get_length_sequences_where(x < np.mean(x))) if x.size > 0 else
0
def longest_strike_above_mean(x): if not isinstance(x, (np.ndarray, pd.Series)): x = np.asarray(x) return np.max(_get_length_sequences_where(x > np.mean(x))) if x.size > 0 else 0
def count_above_mean(x): m = np.mean(x) return np.where(x > m)[0].size
def count_below_mean(x): m = np.mean(x) return np.where(x < m)[0].size
def last_location_of_maximum(x): x = np.asarray(x) return 1.0 - np.argmax(x[::-1]) / len(x) if len(x) > 0 else np.NaN
def first_location_of_maximum(x): if not isinstance(x, (np.ndarray, pd.Series)): x = np.asarray(x) return np.argmax(x) / len(x) if len(x) > 0 else np.NaN
def last_location_of_minimum(x): x = np.asarray(x) return 1.0 - np.argmin(x[::-1]) / len(x) if len(x) > 0 else np.NaN
def first_location_of_minimum(x): if not isinstance(x, (np.ndarray, pd.Series)): x = np.asarray(x) return np.argmin(x) / len(x) if len(x) > 0 else np.NaN
def percentage_of_reoccurring_values_to_all_values(x): if len(x) == 0: return np.nan unique, counts = np.unique(x, return_counts=True) if counts.shape[0] == 0: return 0 return np.sum(counts > 1) / float(counts.shape[0])
def percentage_of_reoccurring_datapoints_to_all_datapoints(x): if len(x) == 0: return np.nan if not isinstance(x, pd.Series): x = pd.Series(x) value_counts = x.value_counts() reoccuring_values = value_counts[value_counts > 1].sum() if np.isnan(reoccuring_values): return 0
return reoccuring_values / x.size
def sum_of_reoccurring_values(x): unique, counts = np.unique(x, return_counts=True) counts[counts < 2] = 0 counts[counts > 1] = 1 return np.sum(counts * unique)
def sum_of_reoccurring_data_points(x): unique, counts = np.unique(x, return_counts=True) counts[counts < 2
] = 0 return np.sum(counts * unique)
def ratio_value_number_to_time_series_length(x): if not isinstance(x, (np.ndarray, pd.Series)): x = np.asarray(x) if x.size == 0: return np.nan
return np.unique(x).size / x.size
def abs_energy(x): if not isinstance(x, (np.ndarray, pd.Series)): x = np.asarray(x) return np.dot(x, x)
def quantile(x, q): if len(x) == 0: return np.NaN return np.quantile(x, q)
def number_crossing_m(x, m): if not isinstance(x, (np.ndarray, pd.Series)): x = np.asarray(x) positive = x > m return np.where(np.diff(positive))[0].size
def absolute_maximum(x): return np.max(np.absolute(x)) if len(x) > 0 else np.NaN
def value_count(x, value): if not isinstance(x, (np.ndarray, pd.Series)): x = np.asarray(x) if np.isnan(value): return np.isnan(x).sum() else: return x[x == value].size
def range_count(x, min, max): return np.sum((x >= min) & (x < max))
def mean_diff(x): return np.nanmean(np.diff(x.values))
定义:特征选择是为机器学习模型构建选择相关特征子集的过程。并非总是存在“数据越多,结果越好”这一真理。包含无关特征(对预测毫无帮助的特征)和冗余特征(与其他特征无关的特征)只会使学习过程不堪重负,并容易导致过拟合。简化模型,使其更容易解释
更短的训练时间和更低的计算成本
数据收集成本更低
避免维度诅咒
我们应该记住,不同的特征子集可以为不同的算法提供最佳性能。因此,它不是机器学习模型训练的一个单独过程。因此,如果我们为线性模型选择特征,最好使用针对这些模型的选择程序,如回归系数或套索的重要性。如果我们为树选择特征,最好使用树导出的重要性。筛选方法根据性能指标选择特征,而不管以后采用哪种机器学习算法。单变量过滤器根据特定标准对单个特征进行评估和排名,而多变量过滤器则对整个特征空间进行评估。过滤器方法有:
在记分卡开发中,WOE编码(见第4.3.2节)和IV通常齐头并进。这两个概念都来自逻辑回归,是信用卡行业的标准做法。IV是一种流行且广泛使用的度量方法,因为与IV相关的变量选择有非常方便的经验法则,如下所述
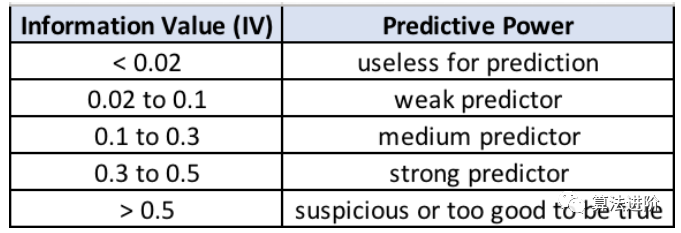
然而,所有这些过滤方法都没有考虑特征之间的相互作用,可能会降低我们的预测能力。我个人只使用方差和相关性来过滤一些绝对不必要的特征。注意:在使用卡方检验或单变量选择方法时,要记住一件事,即在非常大的数据集中,大多数特征将显示较小的p值,因此看起来它们具有很高的预测性。这实际上是样本大小的影响。因此,在使用这些程序选择特征时应该小心。超小的p值并不能突出超重要的特征,而是表明数据集包含太多的样本。注意:相关特征不一定影响模型性能(树等),但高维度会,过多的特征会损害模型的可解释性。因此,减少相关特征总是更好的。包装器使用搜索策略在可能的特征子集空间中搜索,并通过ML算法的性能质量评估每个子集。实际上,搜索策略和算法的任何组合都可以用作包装器。它的特点是:最常见的搜索策略组是顺序搜索,包括正向选择、反向排除和穷尽搜索。随机搜索是另一种流行的选择,包括遗传等进化计算算法和模拟退火。包装器中的另一个关键要素是停止条件。什么时候停止搜索?一般来说有三个:前向特征选择首先根据预设评估标准单独评估所有特征,并选择产生最佳性能算法的特征。在第二步中,它评估所选特征和第二个特征的所有可能组合,并根据相同的预设标准选择产生最佳性能算法的组合。预设标准可以是roc_auc(用于分类)和r平方(用于回归)。这种选择过程被称为贪婪,因为它评估了所有可能的单、双、三等特征组合。因此,它在计算上非常昂贵,有时,如果特征空间很大,甚至不可行。有一个专门针对python的包可以实现这种特征选择:mlxtend反向特征选择首先使用所有特征拟合模型。然后它删除一个特征。它会删除一个对特定评估标准产生最高性能算法(统计上最不显著)的特征。在第二步中,它会删除第二个特征,即再次产生最佳性能算法的特征。然后它继续删除特征,直到满足特定标准。例如,预设标准可以是roc_auc用于分类,r平方用于回归。在穷举特征选择中,通过优化特定机器学习算法的指定性能指标,在所有可能的特征子集中选择最佳特征子集。例如,如果分类器是逻辑回归,数据集由4个特征组成,则算法将评估所有15个特征组合,如下所示:1个特征的所有可能组合
2个特征的所有可能组合
3个特征的所有可能组合
并选择能够产生最佳性能(例如,分类准确率)的逻辑回归分类器。这种穷举搜索的计算成本非常高。在实践中,由于这种计算成本,它很少被使用。嵌入式方法结合了过滤器和包装器方法的优点。学习算法利用其自身的变量选择过程,同时进行特征选择和分类。常见的嵌入式方法包括Lasso和各种基于树的算法。其特征为:正则化包括对机器学习模型的不同参数添加惩罚,以减少模型的自由度。因此,模型不太可能适应训练数据的噪声,因此不太可能过拟合。在线性模型正则化中,对每个预测因子乘的系数应用惩罚。对于线性模型,通常有三种正则化:从不同类型的正则化中,Lasso(L1)具有能够将某些系数收缩为零的特性。因此,可以从模型中删除该特征。对于线性回归和逻辑回归,我们可以使用 Lasso 正则化来删除不重要的特征。请记住,增加惩罚将增加删除的特征数量。因此,你需要密切关注并监控,不要将惩罚设置得太高,以至于删除甚至重要的特征,也不要设置得太低,以至于不删除不重要的特征。话虽如此,如果惩罚过高,重要特征被删除,你应该注意到算法性能的下降,然后意识到你需要减少正则化。正规化是一个很大的主题。有关信息,您可以在这里参考:随机森林是最流行的机器学习算法之一。它们之所以如此成功,是因为它们通常具有很好的预测性能、低过拟合和易于解释性。这种可解释性是由于可以直接得出每个变量在树决策中的重要性。换句话说,很容易计算出每个变量对决策的贡献程度。
随机森林是一种bagging算法,由一堆基础估计器(决策树)组成,每个基础估计器都是从数据集中随机抽取观测值和随机抽取特征构建的。不是每棵树都看到所有特征或所有观测值,这保证了树之间是去相关的,因此不容易过拟合。每棵树也是基于单个特征或特征组合的一系列是非问题。在每次分裂时,问题将数据集分为两个桶,每个桶中的观测值之间更相似,并且与其他桶中的观测值不同。因此,每个特征的重要性是由每个桶的“纯度”决定的。对于分类,杂质的度量是基尼杂质或信息增益/熵。对于回归,杂质的度量是方差。因此,在训练树时,可以计算每个特征减少杂质的程度。特征减少杂质越多,特征就越重要。在随机森林中,每个特征的杂质减少可以在树之间进行平均,以确定变量的最终重要性。使用树衍生的特征重要性来选择特征是一种非常简单、快速且通常准确的方法,可以为机器学习选择好的特征。特别是,如果你打算构建树方法。然而,与在没有相关对应物的情况下构建树时的重要性相比,相关特征在树中将以相似且降低的重要性显示出来。与使用随机森林导出的特征重要性选择特征类似,我们可以根据梯度提升树导出的重要性选择特征。我们可以一次性完成,也可以以递归方式完成,这取决于我们有多少时间、数据集中有多少特征以及它们是否相关。特征选择的一种流行方法是对特定变量的值进行随机洗牌,并确定该置换如何影响机器学习算法的性能指标。换句话说,该想法是对每个特征的值进行置换,一次一个,并测量置换对机器学习模型的准确性、roc_auc或mse的降低程度。如果变量很重要,这是高度预测性的,那么它们的值的随机置换将大大降低这些指标中的任何一个。相反,不重要/非预测性变量应该对我们评估的模型性能指标几乎没有影响。根据机器学习算法得出的特征重要性对特征进行排名:可以是树重要性,或 LASSO/Ridge,或线性/逻辑回归系数。
删除一个特征(最不重要的特征),并利用剩余的特征构建机器学习算法。
计算你选择的性能指标:roc-auc、mse、rmse、准确率。
如果指标下降超过任意设置的阈值,则该特征很重要,应该保留。否则,我们可以删除该特征。
- 重复步骤2-4,直到所有特征都被删除(并因此被评估),并且性能下降得到评估。
该方法结合了诸如封装器之类的选择过程和来自诸如嵌入式方法之类的ML模型的特征重要性推导,因此被称为混合方法。该方法与反向特征选择的不同之处在于,它不会首先删除所有特征以确定删除哪一个。它根据机器学习模型得出的重要性删除最不重要的特征。然后,它评估该特征是否应该删除。因此,它在选择过程中只删除每个特征一次,而反向特征选择在选择的每一步都删除所有特征。因此,这种方法比包装器方法更快,通常比嵌入式方法更好。在实践中,它非常有效。它也考虑了相关性(取决于你设置任意性能下降阈值的严格程度)。不利的一面是,评估性能下降以决定保留或删除特征是任意设置的。下降越小,选择的功能越多,反之亦然。正如我们在第4.3.2节中提到的,随机森林对高度相关的特征赋予相同或相似的重要性。此外,当特征相关时,如果没有相关特征,构建的树的重要性低于特征本身的重要性。因此,我们可以通过递归删除一个特征,并在每一轮重新计算重要性,而不是一次性地(从所有初始特征中)根据重要性删除特征,从而得到更好的选择。在这种情况下,当删除与另一个特征高度相关的特征时,剩余特征的重要性就会增加。这可能导致更好的子集特征空间选择。不利的一面是,构建多个随机森林非常耗时,特别是当数据集包含大量特征时根据机器学习算法得出的特征重要性对特征进行排名:可以是树重要性,或 LASSO/Ridge,或线性/逻辑回归系数。
构建一个只有一个特征(最重要的特征)的机器学习模型,并计算模型的性能指标。
添加一个最重要的特征,并利用添加的特征和前几轮中的任何特征构建机器学习算法。
计算你选择的性能指标:roc-auc、mse、rmse、accuracy。
如果指标增加超过任意设置的阈值,则该特征很重要,应该保留。否则,我们可以删除该特征。
- 重复步骤2-5,直到所有特征都已被删除(并因此被评估),并且性能下降得到了评估。
此方法与向前特征选择之间的区别是相似的。它不会首先查找所有特征以确定添加哪个特征,因此它比包装器更快。数据泄露是指使用训练数据集以外的信息来创建模型。结果是你可能创建了过于乐观的模型,这些模型实际上毫无用处,不能用于生产。该模型在训练和测试数据上都显示出很好的结果,但事实上,这不是因为你的模型真的具有良好的泛化能力,而是因为它使用了测试数据中的信息。众所周知,使用交叉验证或至少在训练和评估模型时分离验证集,但人们很容易在特征工程和选择过程中忘记这样做。请记住,测试数据集不得以任何方式用于对模型做出选择,包括特征工程和选择。参考资料:
1、《A Short Guide for Feature Engineering and Feature Selection》
2、《 Penalized feature selection and classification in bioinformatics》
3、《 Least angle and ℓ1 penalized regression: A review》