代码逐行注释|用PyTorch实现深度学习的时间序列预测（基于LSTM循环神经网络）

大家可能没有注意过，人类一直在不自觉地对各种事物进行预测——哪怕是最微小或看似无关紧要的事物。

例如，装水的时候我们会预测什么时候能装满杯子。

在过马路时，我们会本能地预判车辆的位置，以确保自己能够安全通过。

在执行这些日常任务时，我们并不需要精确了解车辆的速度或水流的速度，这些复杂的计算对我们来说似乎是自然而然、水到渠成的事情。

这些预测能力是通过多年的生活经验、学习和练习，在无数次的实践过程中逐渐培养起来的。

然而，当我们试图主动预测大规模现象（如天气变化或未来一年的经济走势）时，情况就变得复杂得多了。

由于这些现象涉及的因素众多且相互关联，我们往往会感到力不从心，难以做出准确的预测。

这时，计算机的强大功能便显得尤为重要——它能够弥补我们在处理看似随机的偶发事件并将其与未来事件相关联方面的不足。

计算机在多次重复执行特定任务方面表现出色——我们可以利用这一优势来预测未来。

为了让大家可以更系统的学习时间序列，小墨学长还为大家准备了神经网络和时间序列的相关学习资料。

本文的数据集和时间序列、神经网络学习资料大家可以任意添加一位小助手获取（记得发送文章标题哦）

什么是“时间序列”？

时间序列是指任何在一段时间内发生的可量化指标或事件，几乎任何事物都可以被视为时间序列。

例如，你一个月内每小时的平均心率、一只股票一年内每天的收盘价，或某个城市一年内每周的车辆事故数量。

只要是在任何统一时间段内记录的信息，都可视为时间序列，

大家可能会注意到，上述每个示例中的事件都有一个频率（如每日、每周、每小时等）和一个持续时间（如一个月、一年、一天等）。

对于时间序列，我们会在整个观察期间以统一的频率记录该指标，换句话说，每条记录之间的时间间隔应该是相同的。

在本教程中，我们将探讨如何使用时间序列形式的过去数据来预测未来可能发生的情况。

目标

算法的目标是接收一系列数值，并预测序列中的下一个数值。

最简单的方法是使用自回归模型，但今天我们将使用循环神经网络（RNN）的深度学习方法来解决这个问题。

数据准备

让我们先来看一个时间序列样本，下面的图表显示了2013年至2018年油价的一些数据。

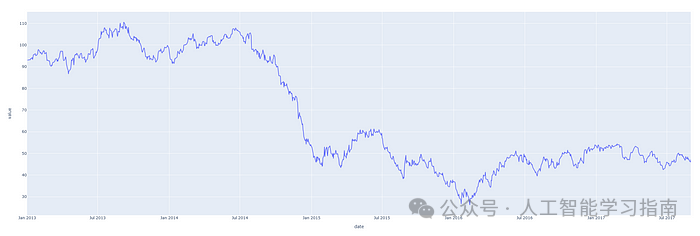
这只是一个在日期轴上绘制的单一数字序列的图，下面的表格显示了该时间序列的前10条记录。

仅查看日期列，就可以明显看出我们拥有每日频率的价格数据。

date        dcoilwtico2013-01-01  NaN2013-01-02  93.142013-01-03  92.972013-01-04  93.122013-01-07  93.202013-01-08  93.212013-01-09  93.082013-01-10  93.812013-01-11  93.602013-01-14  94.27

许多机器学习模型在归一化数据上表现更佳，归一化数据的标准方法是将数据转换，使得每列的均值为0，标准差为1。

下面的代码使用scikit-learn库提供了实现这一操作的方法。

from sklearn.preprocessing import StandardScaler  # 导入数据标准化工具
# 初始化一个空字典，用于存储每列数据对应的标准化工具scalers = {}
# 对数据框 `df` 中的每一列数据进行标准化工具的拟合for x in df.columns:      # 对每列数据拟合一个标准化工具，并存入字典中    scalers[x] = StandardScaler().fit(df[x].values.reshape(-1, 1))
# 创建一个副本 `norm_df`，用于存储标准化后的数据norm_df = df.copy()
# 使用拟合好的标准化工具对数据进行变换for i, key in enumerate(scalers.keys()):      # 对数据的第 i 列进行标准化，`reshape(-1, 1)` 是因为输入需要是二维的    norm = scalers[key].transform(norm_df.iloc[:, i].values.reshape(-1, 1))    # 将标准化后的数据赋值回对应列    norm_df.iloc[:, i] = norm

我们还需确保数据具有统一的频率——在本例中，我们拥有这5年来每天的油价数据，因此这一点得到了很好的满足。

如果你的数据并非如此，Pandas提供了几种不同的方法来重新采样数据以适应统一的频率。

序列化

实现这一点后，我们将使用时间序列生成固定长度的片段或序列。

在记录这些序列时，我们还将记录紧跟在该序列之后出现的值。例如：假设我们有一个序列：[1, 2, 3, 4, 5, 6]。

选择序列长度为3时，我们可以生成以下序列及其关联的目标值：

[序列]：目标值

[1, 2, 3] → 4

[2, 3, 4] → 5

[3, 4, 5] → 6

另一种看待这个问题的方式是，我们定义了要回溯多少步来预测下一个值。

我们将这个值称为训练窗口，将要预测的值数称为预测窗口。

在本例中，它们分别为3和1，下面的函数详细说明了如何实现这一点。

# 定义一个函数，用于生成时间序列的输入序列和目标值def generate_sequences(df: pd.DataFrame, tw: int, pw: int, target_columns, drop_targets=False):    '''    参数说明:    df: Pandas DataFrame，表示单变量或多变量的时间序列数据    tw: Training Window，整数，表示输入序列的时间步数（向后看多少步）    pw: Prediction Window，整数，表示目标预测的时间步数（向前预测多少步）    target_columns: 目标列的名称列表，表示要预测的列    drop_targets: 布尔值，可选，是否从数据集中删除目标列
    返回值:    一个字典，包含所有生成的输入序列和目标值，每个序列和目标值用键值对存储    '''


    
    data = dict()  # 用字典存储生成的序列和目标值    L = len(df)  # 获取数据框的总长度
    # 遍历整个数据框，生成输入序列和目标值    for i in range(L - tw):          # 如果选择了删除目标列        if drop_targets:            df.drop(target_columns, axis=1, inplace=True)  # 从数据框中移除目标列
        # 获取当前时间窗口（输入序列）        sequence = df[i:i + tw].values  # 从第 i 行开始，取长度为 tw 的数据作为输入序列                # 获取当前时间窗口之后的预测目标        target = df[i + tw:i + tw + pw][target_columns].values  # 从第 i + tw 行开始，取长度为 pw 的目标值                # 将输入序列和目标值存入字典中，以 i 作为键        data[i] = {'sequence': sequence, 'target': target}        # 返回包含所有序列和目标值的字典    return data

PyTorch要求我们按照以下方式将数据存储在Dataset类中：

class SequenceDataset(Dataset):
  def __init__(self, df):    self.data = df
  def __getitem__(self, idx):    sample = self.data[idx]    return torch.Tensor(sample['sequence']), torch.Tensor(sample['target'])    def __len__(self):    return len(self.data)

然后，我们可以使用PyTorch DataLoader来迭代数据，使用DataLoader的好处是，它内部处理批处理和混洗，因此我们无需自己实现这些功能。

执行以下代码后，训练批次便准备就绪：

# 定义模型的训练参数BATCH_SIZE = 16  # 训练的批量大小split = 0.8  # 训练集和测试集的划分比例，80%用于训练，20%用于测试
# 使用之前定义的 `generate_sequences` 函数生成时间序列数据# 参数说明：# - `norm_df.dcoilwtico.to_frame()`: 选取特定列 'dcoilwtico'，并转换为 DataFrame 格式# - `sequence_len`: 输入序列的长度（定义的时间步数）# - `nout`: 预测步数# - `'dcoilwtico'`: 目标列名称sequences = generate_sequences(norm_df.dcoilwtico.to_frame(), sequence_len, nout, 'dcoilwtico')
# 使用 `SequenceDataset` 类包装生成的时间序列数据，形成 PyTorch 数据集dataset = SequenceDataset(sequences)
# 根据定义的训练/测试比例划分数据集train_len = int(len(dataset) * split)  # 计算训练集的样本数量lens = [train_len, len(dataset) - train_len]  # 列表存储训练集和测试集的长度# 使用 PyTorch 的 `random_split` 方法将数据集划分为训练集和测试集train_ds, test_ds = random_split(dataset, lens)
# 为训练集和测试集分别创建数据加载器 (DataLoader)# 参数说明：# - `train_ds`: 训练数据集# - `BATCH_SIZE`: 每批次加载的数据量# - `shuffle=True`: 是否打乱数据集，保证训练过程的随机性# - `drop_last=True`: 如果最后一个批次数据量小于 `BATCH_SIZE`，是否丢弃该批次trainloader = DataLoader(train_ds, batch_size=BATCH_SIZE, shuffle=True, drop_last=True)testloader = DataLoader(test_ds, batch_size=BATCH_SIZE, shuffle=True, drop_last=True)

在每次迭代中，DataLoader将生成16个（批大小）序列及其关联的目标值，我们将这些值传递给模型。

模型架构

下面的类在PyTorch中定义了这种架构，我们将使用一个LSTM层，后面跟着一些用于模型回归部分的密集层，并在它们之间添加丢弃层，该模型将为每个训练输入输出一个单一值。

class LSTMForecaster(nn.Module):    """    定义一个用于时间序列预测的 LSTM 模型。    """
    def __init__(self, n_features, n_hidden, n_outputs, sequence_len, n_lstm_layers=1, n_deep_layers=10, use_cuda=False, dropout=0.2):        '''        初始化 LSTM 模型参数：        n_features: 输入特征的数量（对于单变量预测，通常为 1）        n_hidden: 每个隐藏层中的神经元数量        n_outputs: 每个训练样本需要预测的输出数量        sequence_len: 预测时需要回顾的时间步长（时间序列长度）        n_lstm_layers: LSTM 层的数量        n_deep_layers: LSTM 后的全连接层数量        use_cuda: 是否使用 GPU 进行计算        dropout: float (0 < dropout < 1)，用于防止过拟合的 dropout 比例        '''        super().__init__()
        self.n_lstm_layers = n_lstm_layers  # LSTM 层数        self.nhid = n_hidden  # 隐藏层神经元数量        self.use_cuda = use_cuda  # 是否使用 CUDA 加速
        # 定义 LSTM 层        self.lstm = nn.LSTM(n_features,                            n_hidden,                            num_layers=n_lstm_layers,                            batch_first=True)  # batch_first=True 表示输入形状为 (batch_size, seq_len, features)
        # LSTM 输出后的第一个全连接层        self.fc1 = nn.Linear(n_hidden * sequence_len, n_hidden)                # Dropout 层，用于减轻过拟合        self.dropout = nn.Dropout(p=dropout)
        # 定义全连接网络（DNN）层        dnn_layers = []        for i in range(n_deep_layers):            # 最后一层连接到输出（形状：n_hidden -> n_outputs）            if i == n_deep_layers - 1:                dnn_layers.append(nn.ReLU())  # 激活函数                dnn_layers.append(nn.Linear(n_hidden, n_outputs))            # 其他中间层（形状：n_hidden -> n_hidden），带 Dropout            else:                dnn_layers.append(nn.ReLU())  # 激活函数                dnn_layers.append(nn.Linear(n_hidden, n_hidden))                if dropout:                    dnn_layers.append(nn.Dropout(p=dropout))
        # 将全连接层编译成顺序网络        self.dnn = nn.Sequential(*dnn_layers)
    def forward(self, x):        '''        定义前向传播过程：        x: 输入数据，形状为 (batch_size, seq_len, features)        '''
        # 初始化 LSTM 的隐藏状态和细胞状态（形状为 [num_layers, batch_size, hidden_size]）        hidden_state = torch.zeros(self.n_lstm_layers, x.shape[0], self.nhid)        cell_state = torch.zeros(self.n_lstm_layers, x.shape[0], self.nhid)
        # 如果使用 CUDA，将隐藏状态移动到 GPU 上        if self.use_cuda:            hidden_state = hidden_state.to(device)            cell_state = cell_state.to(device)
        self.hidden = (hidden_state, cell_state)  # 初始化隐藏状态
        # 前向传播        x, h = self.lstm(x, self.hidden)  # 通过 LSTM 层        x = self.dropout(x.contiguous().view(x.shape[0], -1))  # 展平 LSTM 的输出 (batch_size, hidden_size * sequence_len)        x = self.fc1(x)  # 通过第一个全连接层        return self.dnn(x)  # 通过全连接网络 (DNN)，最终输出预测值

这个类是我构建的一个即插即用的Python类，能够基于我们选择的参数动态构建任何大小的这种类型神经网络——因此，你可以根据需要调整n_hidden和n_deep_players参数，为你的模型添加或删除参数。

参数越多，模型越复杂，训练时间越长，因此请根据你的用例选择最适合你数据的参数。

作为任意选择，让我们创建一个具有5个全连接层的长短期记忆（LSTM）模型，每个层有50个神经元，每个训练批次中的每个训练示例最终输出一个单一值。

在这里，sequence_len指的是训练窗口，nout定义了要预测的步骤数；

将sequence_len设置为180，nout设置为1，意味着模型将回顾180天（半年）的数据来预测明天会发生什么。

# 设置模型参数nhid = 50  # 隐藏层的神经元数量（即 LSTM 隐藏状态的维度）n_dnn_layers = 5  # 全连接网络（DNN）中的隐藏层数量nout = 1  # 输出窗口大小，即每个训练样本需要预测的时间步数sequence_len = 180  # 训练窗口大小，即用于预测的时间步数（输入序列长度）
# 输入特征的数量（由于这是单变量时间序列分析，这里设置为 1；多变量分析可在后续进行扩展）ninp = 1
# 设备选择（使用 CPU 或 GPU）USE_CUDA = torch.cuda.is_available()  # 检测是否有可用的 GPUdevice = 'cuda' if USE_CUDA else 'cpu'  # 如果有 GPU 可用，则选择 GPU，否则选择 CPU
# 初始化模型model = LSTMForecaster(    ninp,  # 输入特征数量    nhid,  # 隐藏层神经元数量    nout,  # 输出窗口大小    sequence_len,  # 输入序列长度    n_deep_layers=n_dnn_layers,  # 全连接网络的隐藏层数量    use_cuda=USE_CUDA  # 是否启用 GPU).to(device)  # 将模型移动到指定设备（CPU 或 GPU）

模型训练

定义了模型后，我们可以选择损失函数和优化器，设置学习率和迭代次数，并开始训练循环。

由于这是一个回归问题（即我们试图预测一个连续值），因此损失函数的一个安全选择是均方误差（MSE）。

这提供了一种稳健的方法来计算实际值与模型预测值之间的误差。计算公式如下：

优化器对象存储并计算反向传播所需的所有梯度。

# 设置学习率和训练轮数lr = 4e-4  # 学习率，控制模型的权重更新幅度n_epochs = 20  # 训练的轮数，即模型将遍历训练集的次数
# 初始化损失函数和优化器criterion = nn.MSELoss().to(device)  # 定义损失函数为均方误差 (MSE)，用于衡量预测值与真实值之间的差异# 使用 .to(device) 将损失函数移动到指定设备（CPU 或 GPU）
optimizer = torch.optim.AdamW(model.parameters(), lr=lr)# 使用 AdamW 优化器（Adam 的变体，添加了权重衰减以减少过拟合）# model.parameters() 将模型的参数传递给优化器进行更新# lr=lr 指定优化器的初始学习率

以下是训练循环。在每个训练迭代中，我们将计算之前创建的训练集和验证集上的损失：

# 定义列表来存储训练和验证损失t_losses, v_losses = [], []  # `t_losses` 用于存储每个 epoch 的训练损失，`v_losses` 用于存储验证损失
# 迭代训练轮次for epoch in range(n_epochs):  # 遍历指定的训练轮数  train_loss, valid_loss = 0.0, 0.0  # 初始化训练损失和验证损失的累积值
  # 训练步骤  model.train()  # 将模型设置为训练模式，启用 dropout 和梯度计算等功能  for x, y in trainloader:  # 遍历训练数据集的每个批次    optimizer.zero_grad()  # 清零优化器中的梯度缓存    x = x.to(device)  # 将输入数据移动到指定设备（CPU 或 GPU）    y = y.squeeze().to(device)  # 将目标值移动到设备并去掉多余的维度    preds = model(x).squeeze()  # 前向传播，计算预测值，并去掉多余维度    loss = criterion(preds, y)  # 计算当前批次的损失    train_loss += loss.item()  # 累加训练损失    loss.backward()  # 反向传播，计算梯度    optimizer.step()  # 根据梯度更新模型参数


    
  epoch_loss = train_loss / len(trainloader)  # 计算当前 epoch 的平均训练损失  t_losses.append(epoch_loss)  # 将训练损失添加到列表中
  # 验证步骤  model.eval()  # 将模型设置为评估模式，禁用 dropout 等训练专用功能  for x, y in testloader:  # 遍历验证数据集的每个批次    with torch.no_grad():  # 禁用梯度计算（节省内存和计算资源）      x, y = x.to(device), y.squeeze().to(device)  # 将数据移动到设备并去掉多余维度      preds = model(x).squeeze()  # 前向传播，计算预测值      error = criterion(preds, y)  # 计算当前批次的损失    valid_loss += error.item()  # 累加验证损失  valid_loss = valid_loss / len(testloader)  # 计算当前 epoch 的平均验证损失  v_losses.append(valid_loss)  # 将验证损失添加到列表中
  # 打印当前 epoch 的训练和验证损失  print(f'{epoch} - train: {epoch_loss}, valid: {valid_loss}')
# 绘制训练和验证损失曲线plot_losses(t_losses, v_losses)

现在模型已训练完毕，我们可以评估预测结果。

推理

在这里，我们将简单地调用我们的训练模型来预测未打乱的数据，并查看预测结果与真实观测值之间的差异。

def make_predictions_from_dataloader(model, unshuffled_dataloader):  model.eval()  predictions, actuals = [], []  for x, y in unshuffled_dataloader:    with torch.no_grad():      p = model(x)      predictions.append(p)      actuals.append(y.squeeze())  predictions = torch.cat(predictions).numpy()  actuals = torch.cat(actuals).numpy()  return predictions.squeeze(), actuals

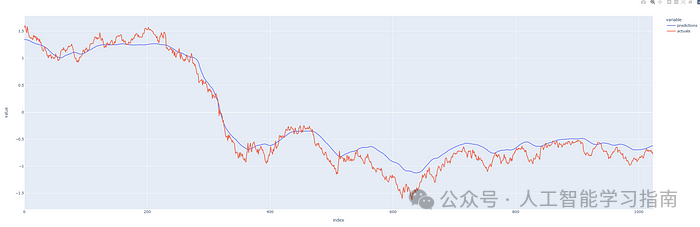
历史石油的标准化预测价格与实际价格

首次尝试，我们的预测结果还算不错！而且验证损失与训练损失一样低，这说明我们没有让模型过拟合，因此可以认为模型的泛化能力良好——这对于任何预测系统而言都至关重要。

针对这一时期油价随时间变化的预测，我们已经有了一个相当不错的估算器，接下来，让我们看看能否用它来预测未来的情况。

预测

如果我们把历史定义为直到预测时刻为止的一系列数据，那么算法就很简单：

从历史数据中获取最新的有效序列（训练窗口长度）。
将该最新序列输入模型，预测下一个值。
将预测值添加到历史数据中。
从第1步开始，进行任意次数的迭代。

这里需要注意的一点是，根据训练模型时选择的参数，预测的时间越远，模型就越容易受到自身偏差的影响，并开始预测平均值。

因此，如果没有必要，我们不想总是预测太远，因为这会影响预测的准确性。

以下函数实现了上述过程：

def


    
 one_step_forecast(model, history):    '''    单步预测函数。        参数:    model: PyTorch 模型对象    history: 表示时间序列最新值的数组，要求 `len(history.shape) == 2`（二维数组）        返回:    单个值，表示序列中下一个值的预测结果。    '''    model.cpu()  # 将模型移动到 CPU    model.eval()  # 将模型设置为评估模式    with torch.no_grad():  # 禁用梯度计算以节省内存和计算时间        pre = torch.Tensor(history).unsqueeze(0)  # 将输入数据转换为张量并添加一个维度        pred = model(pre)  # 使用模型进行前向预测    return pred.detach().numpy().reshape(-1)  # 将预测结果转换为 NumPy 数组并展平为一维数组
def n_step_forecast(data: pd.DataFrame, target: str, tw: int, n: int, forecast_from: int=None, plot=False):    '''    多步预测函数。        参数:    data: pandas 数据框，包含时间序列数据    target: 目标列名称，表示需要预测的时间序列    tw: 训练窗口大小（训练时所需的历史步数）    n: 整数，定义预测未来的步数    forecast_from: 整数，定义从哪个索引开始预测。为 None 时从数据末尾预测    plot: 布尔值，True 表示生成预测结果的可视化图表，False 表示不生成        返回:    包含预测值和实际值的数据框。    '''    history = data[target].copy().to_frame()  # 复制目标列作为历史数据
    # 根据预测的起始点生成初始序列输入    if forecast_from:        pre = list(history[forecast_from - tw : forecast_from][target].values)  # 从 `forecast_from` 开始获取窗口内的值    else:        pre = list(history[target])[-tw:]  # 如果 `forecast_from` 为 None，则使用序列末尾的窗口值
    # 调用 `one_step_forecast` n 次，并将预测值附加到序列中    for i, step in enumerate(range(n)):        pre_ = np.array(pre[-tw:]).reshape(-1, 1)  # 获取最近的 `tw` 个值并调整形状        forecast = one_step_forecast(model, pre_).squeeze()  # 调用单步预测函数        pre.append(forecast)  # 将预测结果附加到序列中
    # 将预测值添加到正确的历史序列时间点    res = history.copy()  # 创建历史数据的副本    ls = [np.nan for i in range(len(history))]  # 初始化 NaN 列表用于存储预测值
    # 处理预测从序列中某个点开始的情况    if forecast_from:        ls[forecast_from : forecast_from + n] = list(np.array(pre[-n:]))  # 将预测值填入对应的索引位置        res['forecast'] = ls        res.columns = ['actual', 'forecast']    else:        fc = ls + list(np.array(pre[-n:]))  # 添加预测值        ls = ls + [np.nan for i in range(len(pre[-n:]))]  # 填充额外的 NaN        ls[:len(history)] = history[target].values  # 设置实际值列        res = pd.DataFrame([ls, fc], index=['actual', 'forecast']).T  # 创建新的数据框
    return res  # 返回包含预测值和实际值的数据框

让我们从序列的中间不同位置开始进行预测，以便将预测结果与实际发生的情况进行比较。

我们编写的预测器代码可以从任何位置开始预测，并且可以进行任何合理数量的步骤。

红线表示预测结果，请注意，图表中的y轴显示的是归一化价格。

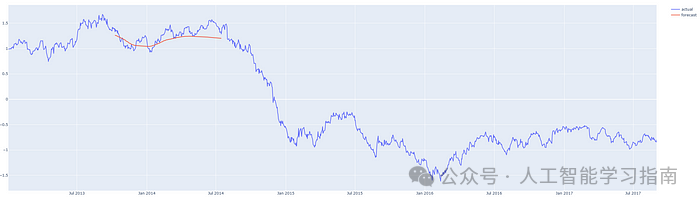
预测从 2013 年第 3 季度开始的 200 天

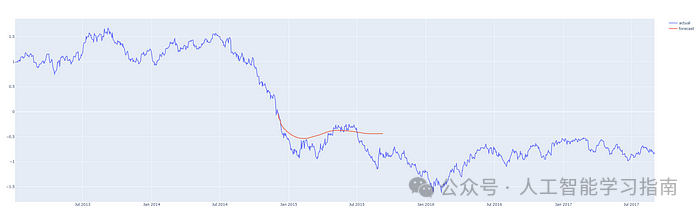
预测从 2014/15 年度开始的 200 天

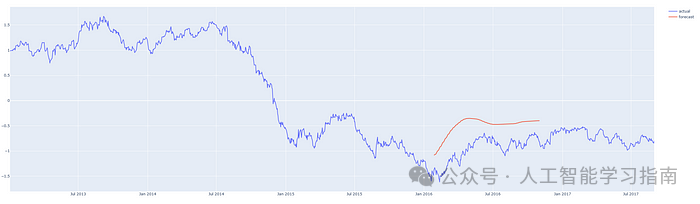
预测从 2016 年第 1 季度开始的 200 天

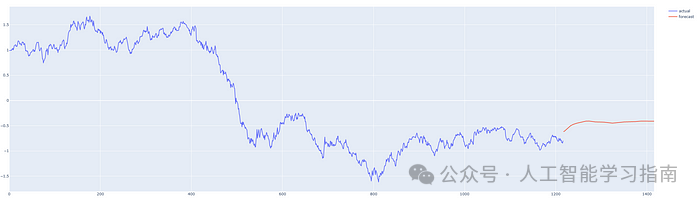
从数据的最后一天开始预测 200 天

而这只是我们尝试的第一个模型配置！如果更多地尝试不同的架构和实现，肯定能让模型训练得更好，预测也更准确。

结论

通过以上步骤，我们拥有了一个可以预测单变量时间序列中接下来会发生什么的模型。

本文只处理了单变量时间序列，即只有一系列单个值，但是，还有方法可以使用多个测量不同事物的序列一起来进行预测，这称为多变量时间序列预测。

这种预测模型真正的魔力在于其LSTM层，以及它作为神经网络的循环层如何处理和记忆序列。

另外我们打磨了一套基于数据与模型方法的 AI科研入门学习方案（已经迭代过 5 次），包含时序、图结构、影像三大实验室，我们会根据你的数据类型来选择合适的实验室，根据规划好的路线学习 只需 5 个月左右（很多同学通过学习已经发表了 sci 二区以下、ei 会议等级别论文）如果需要发高区也有其他形式。

人工智能系统班学习路线

大家感兴趣可以直接添加小助手微信：ai0808q 通过后回复咨询既可！

大家想自学的我还给大家准备了一些机器学习、深度学习、神经网络资料大家可以看看以下文章（文章中提到的资料都打包好了，都可以直接添加小助手获取）

人工智能资料分享

零基础学习路线（点击图片即可跳转）

深度学习中文教程书（点击图片即可跳转）

神经网络学习资料（点击图片即可跳转）

大家觉得这篇文章有帮助的话记得分享给你的死党、闺蜜、同学、朋友、老师、敌蜜！

B站：AI秃秃学长小墨

关注小墨

获取最新AI技能+最肝AI干货