量子计算
量子信息和计算的基本单位是量子比特(qubit),其状态可以是0、1或两者的叠加。量子比特的状态用Dirac的ket符号表示,满足单位范数条件:|α₀|² + |α₁|² = 1。测量会使量子比特的状态坍缩为经典比特,概率为|αₓ|²。量子比特可以通过可逆的单位操作(量子门)进行状态转换。Shor算法和Grover算法为量子算法研究带来了理论上的量子加速。实现这些算法需要大量的量子比特和良好的错误纠正,但当前的量子设备(NISQ设备)尚未达到此要求。量子机器学习(QML)是一个新兴领域,旨在充分利用NISQ设备。
量子机器学习
QML常用的两步方法:变分量子电路(VQC)和经典优化器。VQC由参数化量子门和固定纠缠门组成。经典数据通过数据嵌入过程编码为量子态。VQC应用参数化单位操作,输出通过测量量子比特获得。VQC参数通过经典优化工具优化,以最小化预定义损失函数。VQC常与经典神经网络结合,形成混合QML模型。一些软件包提供高效计算混合QML模型梯度的工具。
多变量时间序列数据包含M个变量,使用大小为L的回溯窗口和大小为T的预测窗口进行预测。预测超过48个时间步被视为长期时间序列预测(LTSF)。在通道独立条件下,单变量时间序列数据分别输入模型,预测未来T个时间步。使用均方误差(MSE)损失函数来衡量真实值与预测值之间的差异。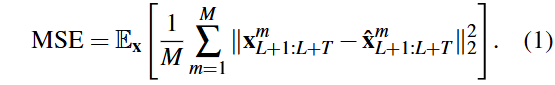
LTSF(长期时间序列预测)研究领域广泛,近年来基于transformer的模型增多。Wen et al.(2023)对transformer基础的LTSF模型进行了全面综述。Zeng et al.(2023)发现简单线性模型在性能上优于一些先进的transformer模型。Zeng et al.提出了三种模型:Linear(单层线性神经网络)、NLinear(输入最后值减去后再加回输出)和DLinear(将时间序列分解为趋势和季节性成分)。DLinear使用两个线性模型分别训练趋势和季节性,最终输出相加得到预测结果。我们将简单的Linear模型改编为QML模型。QuLTSF是一个混合量子机器学习模型,包含输入经典层、隐藏量子层和输出经典层。输入经典层将L个特征映射为2N长度的向量,输出为y₁。
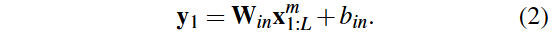
隐藏量子层使用幅度嵌入将y₁编码为量子态|φ_in⟩,并采用硬件高效的变分量子电路(VQC)。VQC由K层组成,每层包含可训练的单量子比特门和固定的CNOT门,输出为|ψ_out⟩。
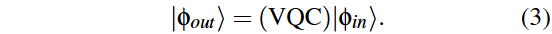
通过计算每个量子比特的Pauli-Z可观察量,得到隐藏量子层的输出y₂。输出经典层将y₂映射为预测的T长度向量,输出为X_LL^{m+L+T}。所有层的参数可以通过PennyLane等软件包联合训练。
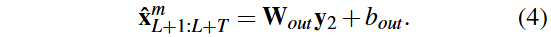
QuLTSF模型在Weather数据集上评估性能。数据集由Max-Planck生物地球化学研究所记录,包含21个气象和环境特征。数据记录于2020年,时间粒度为10分钟,共52,696个时间戳。数据划分:70%用于训练,20%用于测试,10%用于验证。
基线
选择三种线性模型(Linear, NLinear, DLinear)作为主要基线。还考虑了几种基于变换器的LTSF模型(FEDformer, Autoformer, Informer)作为其他基线。变换器模型已被证明优于传统统计模型(如ARIMA)和其他深度学习模型(如LSTM, DeepAR),因此不包括这些模型。
评估指标
在当前研究中,使用均方误差(MSE)和平均绝对误差(MAE)作为评估指标。
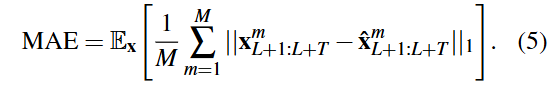
超参数
量子比特数 N = 10,隐藏量子层的 VQC 层数 K = 3。使用 Adam 优化器(Kingma 和 Ba, 2017)训练模型,目标是最小化训练集上的均方误差(MSE)。
结果
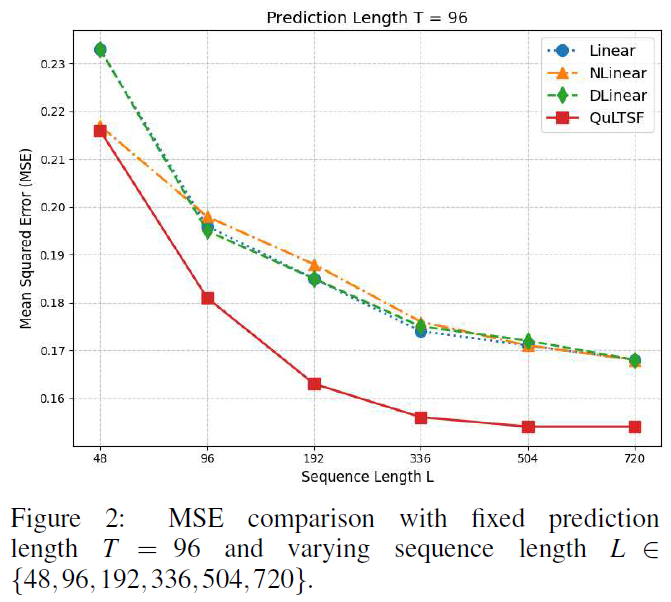
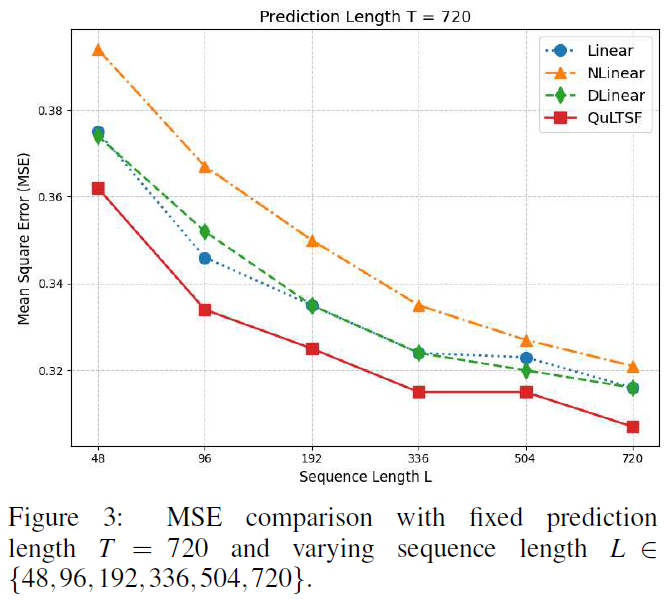
选择固定序列长度L=336,预测长度T为{96,192,336,720},比较QuLTSF与6个基线模型的MSE和MAE,QuLTSF在所有情况下均优于基线模型。为验证QuLTSF与基线线性模型的表现,进行不同序列长度L的实验,固定预测长度T=96和T=720,结果显示QuLTSF始终优于基线线性模型。

讨论
QuLTSF使用通用的硬件高效变换,选择合适的变换是QML中的研究方向(Du et al., 2022)。针对不同数据集寻找更好的QML LTSF模型变换仍是一个开放问题,参数化的两量子比特旋转门是潜在方法(You et al., 2021)。高效的数据预处理(如反向实例归一化)可减轻训练与测试数据之间的分布偏移,已在PatchTST(Nie et al., 2023)和MTST(Zhang et al., 2024)中应用。PatchTST和MTST在性能上优于线性模型(Zeng et al., 2023),但QuLTSF在有限设置下表现相当或更优。在设置(L = 336, T = 720)下,PatchTST、MTST和QuLTSF的MSE分别为0.320、0.319和0.315;在(L = 336, T = 336)下,MSE分别为0.249、0.246和0.248。效率高的数据预处理可能提升QML模型的结果。
本文提出了QuLTSF,一种简单的混合量子机器学习模型用于长期时间序列预测(LTSF)。QuLTSF结合了变分量子电路(VQC)和经典线性神经网络,形成高效的LTSF模型。简单线性模型优于复杂的基于变换器的LTSF模型,且引入隐藏量子层进一步提升了性能。研究为未来LTSF研究中的混合量子机器学习模型应用开辟了新方向。