不久前看过一篇剑桥博士的论文,强调了贝叶斯推断是深度学习的下一个风口。不得不说,确实很有预见性,贝叶斯推断的核心优势在于概率框架的灵活性和对不确定性的显式建模能力,天然适合解决传统深度学习黑箱性、数据饥渴等问题。
再加上,贝叶斯推断与深度学习的融合现在正突破传统AI的能力边界,各领域对可靠的不确定性量化需求与日俱增,当下贝叶斯推断的研究重要性毋庸置疑。我简单看了一下,已经有不少高区成果发表了,趁现在还不算卷,感兴趣的论文er抓紧上车。
至于创新方向,未来重点可能在算法效率、架构设计(尤其是贝叶斯深度学习架构)等方面,还需注意解决计算与理论问题。我已备好11篇贝叶斯推断前沿论文+代码,需要参考的可无偿获取。
扫码添加小享,回复“贝叶斯推断”
免费获取
全部论文+开源代码

A geometric ensemble method for Bayesian inference
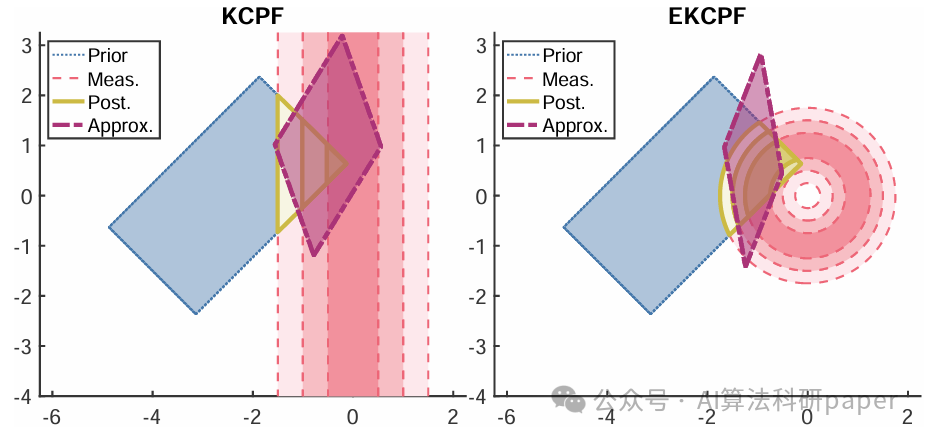
方法:论文提出了一种基于凸多面体的几何方法来近似贝叶斯推断。通过将先验和测量不确定性表示为凸多面体上的均匀分布,并利用这些几何结构进行更新和估计,从而实现对复杂问题的高效贝叶斯推断。
创新点:
- 提出了一种基于凸多面体的几何集合方法,将贝叶斯推理中的先验和测量不确定性表示为凸多面体上的均匀分布,为贝叶斯推断提供了一种新的几何视角。
- 开发了多种滤波器,包括扩展和卡尔曼化版本,这些滤波器能够处理线性和非线性测量问题。
- 提出了基于集合的滤波器,这些方法在低维和高维问题上均表现出良好的性能,验证了新方法的适用性。
Can Transformers Learn Full Bayesian Inference in Context?
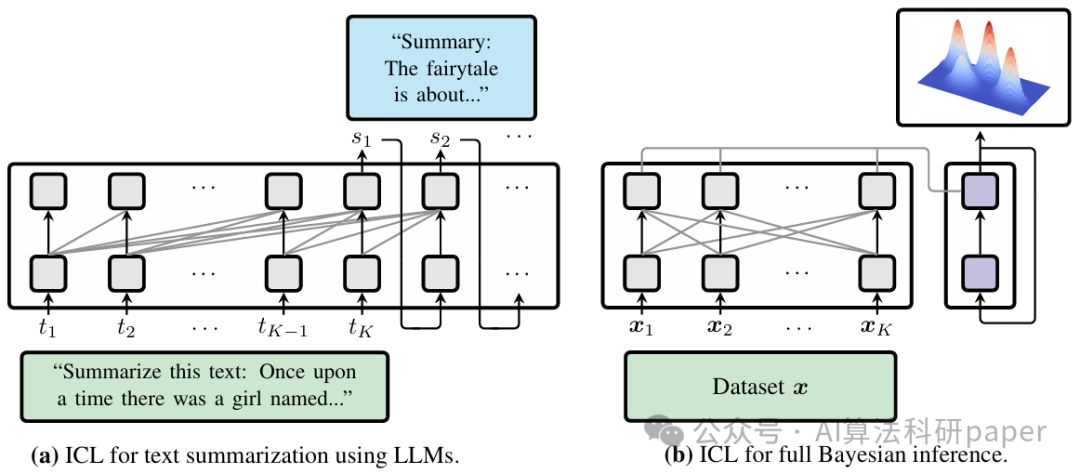
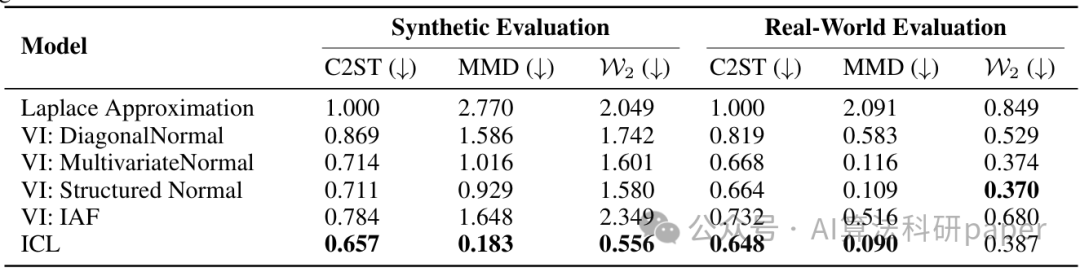
方法:论文提出了一种基于Transformer的方法,通过在上下文中学习,能够直接从数据中进行完整的贝叶斯推断。它利用连续归一化流来建模复杂的后验分布,无需显式的参数更新或对后验分布进行假设。实验表明,该方法在多种模型和真实数据集上的表现与现有的贝叶斯推断方法相当或更好。
创新点:
- 提出了一种基于Transformer的框架,利用连续归一化流在上下文中直接学习复杂的后验分布。
- 通过从模型的联合分布 中采样来训练Transformer,使其能够适应各种输入并快速生成后验分布的样本。
- 在广义线性模型和潜在因子模型等常见统计模型上,该方法性能优于或等同于现有贝叶斯推断方法。
扫码添加小享,回复“贝叶斯推断”
免费获取全部论文+开源代码

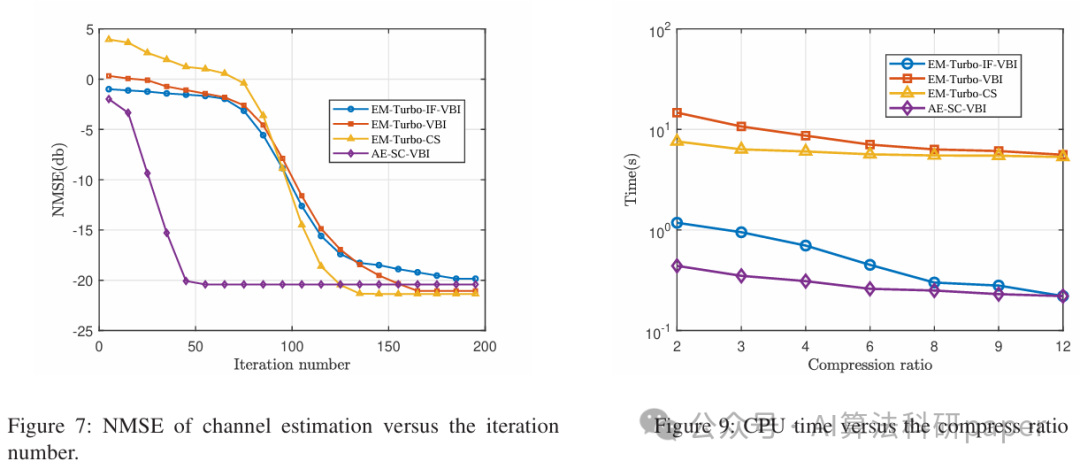
Subspace Constrained Variational Bayesian Inference for Structured Compressive Sensing with a Dynamic Grid
方法:论文提出了一种基于贝叶斯推断的交替估计框架,用于恢复动态网格下的结构化稀疏信号。核心方法是子空间约束变分贝叶斯推断(SC-VBI),通过低维子空间约束来避免高维矩阵求逆,降低计算复杂度。该框架结合动态网格估计和结构化稀疏推理模块,实现了快速收敛和高性能的信号恢复。
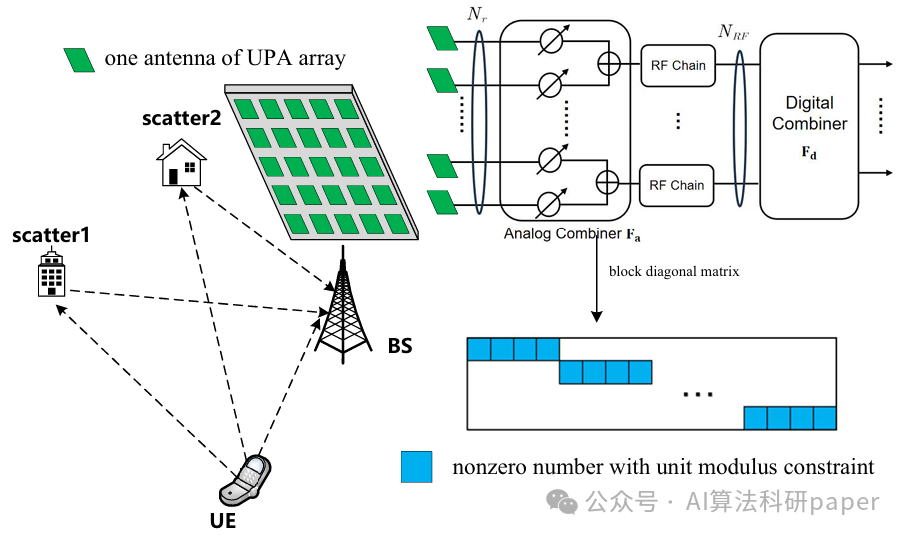
创新点:
- 提出了一种交替估计框架,结合子空间约束变分贝叶斯推断、动态网格估计和结构化稀疏推理模块,实现了高效信号恢复。
- 通过子空间约束矩阵求逆替代高维矩阵求逆,显著降低了计算复杂度,同时保持了算法的收敛速度和性能。
- 证明了SC-VBI算法的收敛性,并通过大规模MIMO信道估计的实验验证了其优越性。
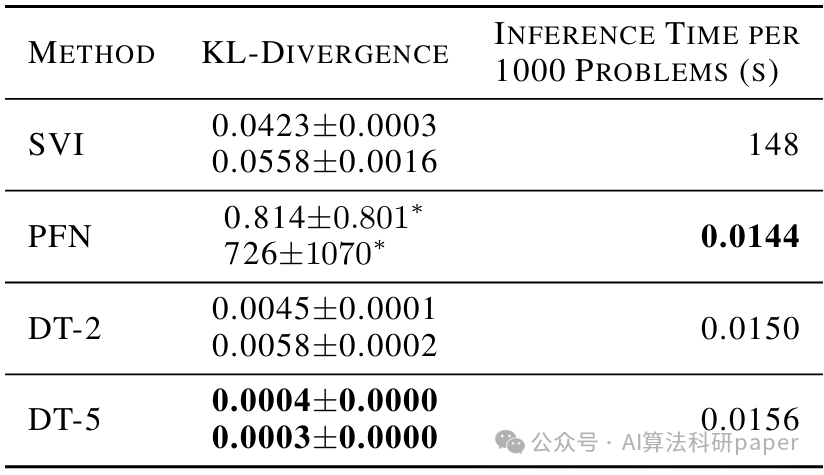
Distribution Transformers: Fast Approximate Bayesian Inference With On-The-Fly Prior Adaptation
方法:论文提出了一种名为“DTs”的方法,用于快速近似贝叶斯推断。它通过将先验分布表示为高斯混合模型,并利用Transformer架构将其转换为后验分布,从而在单次前向传播中完成推断。该方法能够在不重新训练的情况下处理多种先验分布,显著减少计算时间,同时保持灵活性和准确性。
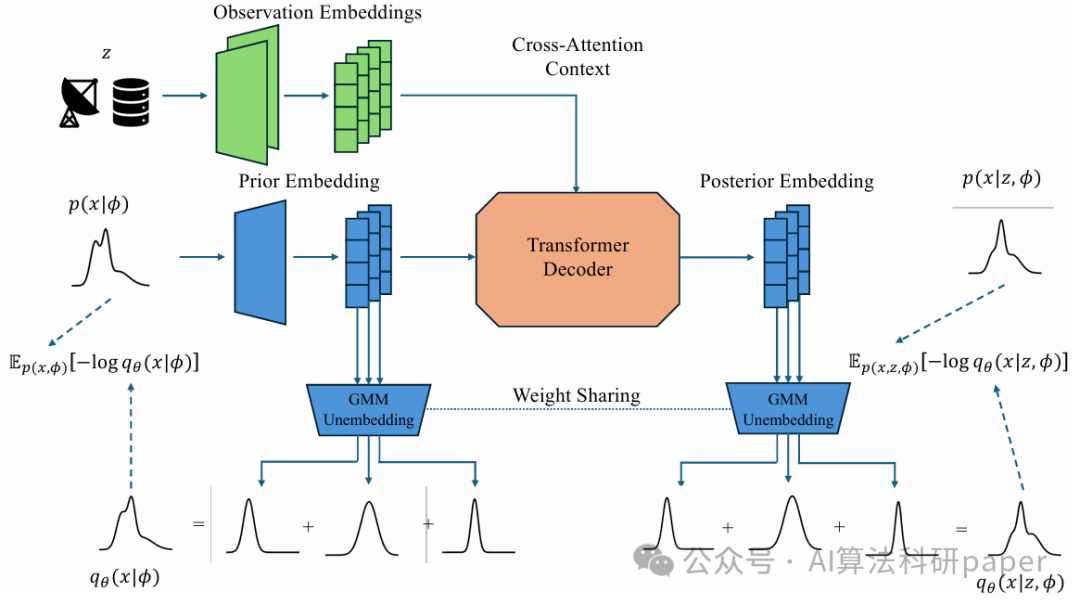
创新点:
- 提出了一种新的架构“DTs”,能够将任意先验分布映射为后验分布,支持动态更新先验而无需重新训练。
- 利用高斯混合模型和Transformer架构,实现了从先验到后验的高效转换,将计算时间从分钟级降低到毫秒级。
- 在多种任务中验证了该方法的优越性能,证明了其在实际应用中的高效性和准确性。
扫码添加小享,回复“贝叶斯推断”
免费获取
全部论文+开源代码
