空间组学 | Nat.Methods | 用可解释的深度学习绘制空间基因表达的地形图

Basic Information

• 英文标题：Mapping the topography of spatial gene expression with interpretable deep learning
• 中文标题：用可解释的深度学习绘制空间基因表达的地形图
• 发表日期：23 January 2025
• 文章类型：Article
• 所属期刊：Nature Methods
• 文章作者：Uthsav Chitra | Benjamin J. Raphael
• 文章链接：https://www.nature.com/articles/s41592-024-02503-3

Abstract

Para_01

1. 空间分辨的转录组学技术提供了组织切片中基因表达的高通量测量，但这些数据的稀疏性使得分析空间基因表达模式变得复杂。
2. 我们通过使用一个称为等深度（isodepth）的量来推导组织切片的地形图——类似于景观中的高度图——来解决这个问题。
3. 等深度的等值线包围了具有不同细胞类型组成的区域，而等深度的梯度则指示了表达变化最大的空间方向。
4. 我们开发了GASTON（基于神经网络的空间转录组学组织梯度分析），这是一种无监督且可解释的深度学习算法，能够同时学习等深度、空间梯度和分段线性表达函数，以建模连续梯度和基因表达中的不连续变化。
5. 我们证明了GASTON能够在多种组织中准确识别空间域和标记基因，大脑中的神经元分化和放电梯度，以及肿瘤微环境中代谢和免疫活动的梯度。

Main

Para_01

1. 基因表达在组织中存在显著差异，这既与组织内细胞类型的空间分布有关，也与通过发育、分化和细胞间通讯等过程引起的局部细胞状态变化有关。
2. 许多基因在组织的某些区域表现出急剧而不连续的变化，通常靠近包含不同细胞类型组合的不同空间域的边界；例如，大脑的不同皮层和新皮层层由某些标记基因的存在与否来区分。
3. 基因表达在组织中也可能连续变化，形成‘梯度’，这些梯度区分了细胞类型或细胞状态，并驱动包括发育和细胞通讯在内的基本生物学过程。
4. 例如，基因表达梯度是海马体中神经元功能异质性的基础，也是肝脏中肝细胞功能异质性的基础，而在肿瘤中，基因表达可能随着与周围基质的距离而连续变化，这是由于氧气梯度或细胞相互作用所致。

Para_02

1. 空间分辨转录组学（SRT）技术生成高通量的空间基因表达测量，量化组织切片中数千个位置的RNA转录本数量。
2. 这些技术能够推断组织中的空间域，并识别具有连续梯度和在空间域内及跨域之间不连续变化的基因和细胞类型。
3. 然而，SRT技术通常只提供转录组的稀疏测量：基于全转录组测序的当前技术覆盖范围有限（每个位置大约500到5,000个独特的分子标识符(UMIs)），而基于成像的技术则测量更小且更有针对性的转录本面板（通常为100到1,000个转录本）。
4. 这种稀疏性显著复杂化了空间基因表达的分析。

Para_03

1. 已经开发了多种计算方法，用于从SRT数据中识别空间域和/或具有空间变化表达的基因。
2. 这些方法通常利用相邻空间位置之间的表达测量值的相关性，以克服单个位置上的稀疏测量问题。
3. 许多方法通过将组织划分为具有大而不连续基因表达变化的子区域来识别不同的空间域，但不建模这些区域内连续的基因表达梯度。
4. 其他一些方法则通过将函数拟合到空间位置上的观察到的转录计数，以测试单个基因的表达是否在空间上变化。
5. 然而，这些方法无法区分空间域内的连续梯度与域之间表达的不连续变化。
6. 更广泛地说，这两种方法都不使用描述空间域边界以及这些域内空间位置相对位置的坐标系统来建模组织切片的几何形状，从而极大地限制了它们识别域内连续基因表达梯度的能力。

Para_04

1. 我们引入了基因表达地形图，这是一种不同的建模方法，用于描述基因表达的空间变化。
2. 我们使用等深线，即组织切片上的一维坐标，来推导出组织切片的地形图，该坐标描述了空间域的排列以及每个空间位置在其相应空间域中的相对位置。
3. 就像地形图通过海拔划分山脉和平原一样，我们的基因表达地形图通过等深线划分空间域。
4. 此外，与景观的海拔一样，等深线在组织切片上连续变化，提供了一个坐标来建模单个基因表达的连续变化。
5. 特别是，我们的地形图描述了基因表达梯度，类似于地形图如何显示某个方向是陡峭的上升还是平坦的高原。

Para_05

1. 我们开发了基于神经网络的空间转录组组织的梯度分析（GASTON），这是一种无监督且可解释的深度神经网络算法，它直接从空间分辨转录组（SRT）数据中学习组织切片的等深线、基因表达的空间梯度向量场以及单个基因的空间表达函数。
2. 特别是，GASTON 将基因表达建模为等深线的分段线性函数，该函数描述了基因表达中的连续梯度和急剧不连续性。
3. 我们证明了 GASTON 学习到的等深线和空间梯度揭示了多个组织切片的几何形状和连续基因表达梯度，涵盖了多种 SRT 技术，包括 10X Genomics Visium 和 Xenium、Slide-SeqV2、MERFISH 和 Stereo-Seq。
4. 在来自小鼠和人类大脑的 SRT 数据上，与现有方法相比，GASTON 更准确地识别出空间域和标记基因，绘制了细胞类型组织的空间变异图，并揭示了神经元放电和分化的空间梯度。
5. GASTON 对结直肠癌（CRC）和乳腺肿瘤样本的 SRT 数据分析识别出肿瘤微环境中代谢、免疫活性和上皮-间质转化（EMT）相关基因表达的梯度。

Results

GASTON learns gene expression topography of a tissue slice

GASTON 学习组织切片的基因表达拓扑结构

Para_01

1. 我们引入了等深量 d，一个模拟组织切片地形的标量，类似于地形图中陆地表面的海拔。
2. 一组等深量 d 相等的等高线将组织切片划分为空间域，而中间等深量的等高线定义了位置在域内的相对位置。
3. 此外，每个位置处的等深量 d 的梯度 ∇d 描述了每个空间域内基因表达的最大变化方向或空间梯度。
4. 这些空间梯度的集合定义了跨组织切片 T 的空间转录组向量场 v（图 1a）。
5. 因此，等深量描述了组织切片的几何结构，即组织中不同空间域的排列，以及每个空间域内的连续变化方向（方法）。

Fig. 1: GASTON, an interpretable deep neural network, learns the topography of a tissue.

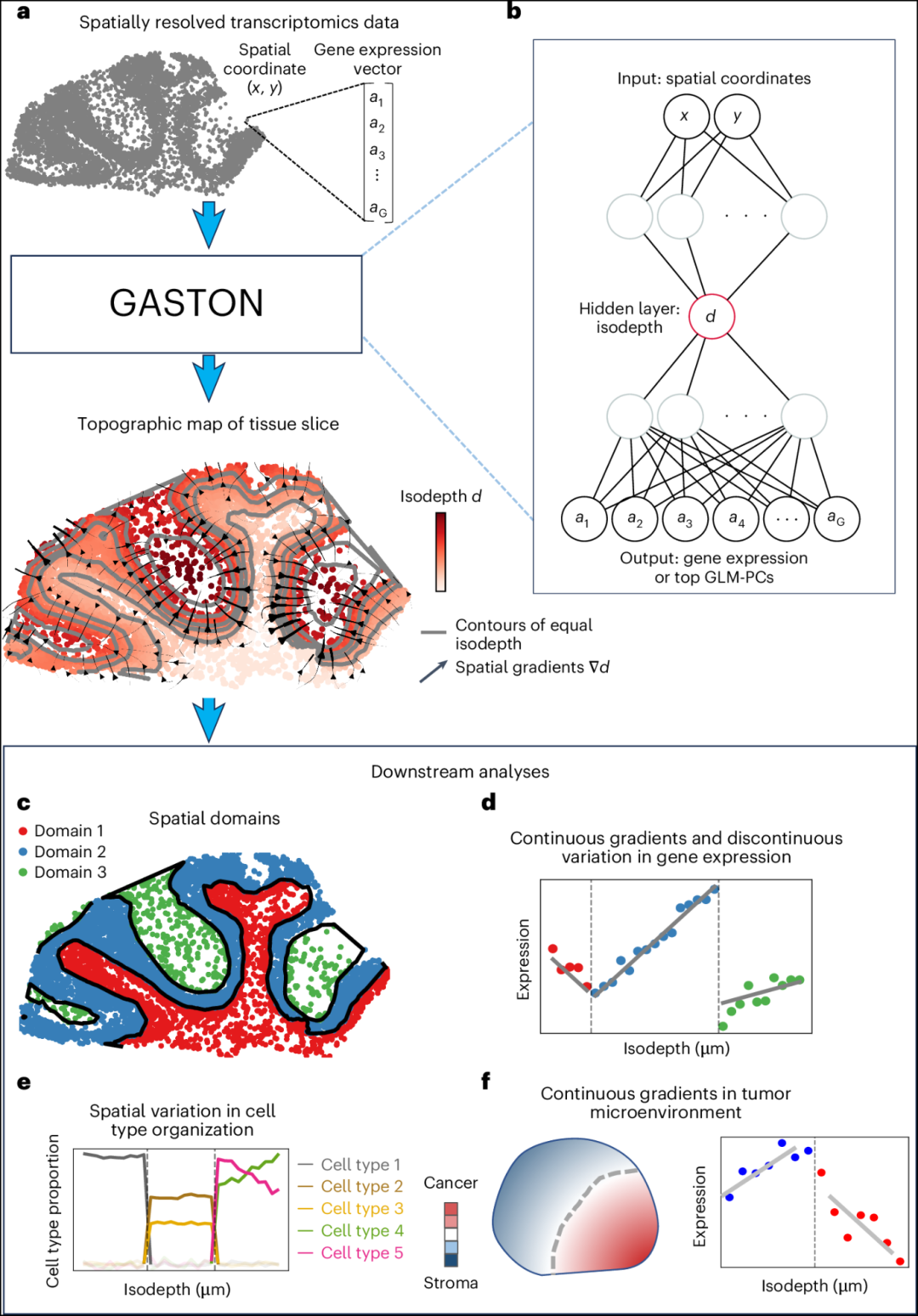
- 图片说明

◉ GASTON 从组织切片中获取 SRT 数据，并输出等深线，这是一种描述组织切片地形图的坐标，其中等深线的轮廓以灰色显示，空间梯度以流线表示。◉ GASTON 训练一个深度神经网络，根据空间坐标预测基因表达，其中等深线是训练后的神经网络中可解释隐藏层的值。◉ GASTON 学到的等深线使得许多下游任务成为可能，包括识别空间域，即由不同细胞类型组成和基因表达模式特征的组织区域。◉ 识别基因在等深线函数中的连续梯度和/或不连续变化。◉ 建模细胞类型组成在等深线函数中的变化。◉ 分析肿瘤微环境中基因表达的连续梯度。

Para_02

1. 为了从SRT数据中学习等深度d，我们开发了GASTON，该模型将每个基因g在空间位置(x, y)的表达式fg(x, y)建模为等深度d(x, y)的分段线性函数：

Para_03

1. 其中，R1，…，RQ 是空间域，αp,g 和 βp,g 分别是第 p 个空间域 Rp 中的截距和斜率。
2. 我们使用分段线性函数，因为它们是一类简单的模型，既可以在每个域内包含基因表达的连续变化，即表达梯度，又允许在域边界处存在表达的不连续性。
3. 每个空间域 Rp 的边界由等深线 d(x, y) 给出（方法）。
4. 我们强调，我们的模型不限制空间域 Rp 必须是连续区域；因此，GASTON 能够建模基因表达的长程空间相关性，与许多仅建模局部空间相关性的现有方法形成对比（方法）。

Para_04

1. GASTON 使用可解释的深度学习模型，以完全无监督的方式联合学习等深 d 和分段线性基因表达函数 fg。
2. 具体来说，GASTON 训练神经网络学习从空间坐标到基因表达特征的复合函数 (h∘d)(x, y)，其中等深 d(x, y) 对应于网络的一个可解释隐藏层（图 1b）。
3. 然后，GASTON 使用分段回归来学习空间域 Rp，以及每个基因 g 的分段线性表达函数 fg 的参数 α 和 β。
4. 我们将在下面展示，GASTON 的可解释方法揭示了有意义的空间域（图 1c），以及基因表达中的连续梯度和不连续性（图 1d）和细胞类型组成（图 1e），涵盖了包括大脑和肿瘤微环境在内的广泛 SRT 技术和生物系统（图 1f）。

GASTON recapitulates the spatial organization of the mouse cerebellum

GASTON 总结了小鼠小脑的空间组织结构

Para_01

1. 我们使用 GASTON 学习了小鼠小脑组织切片中的等深度 d 和空间梯度 ∇d，该切片中通过 Slide-SeqV2 平台测量了 9,985 个空间位置上的 23,096 个转录本的表达。
2. 学习到的等深度 d 提供了小脑分层几何结构的地形图，包括小脑不同层的边界，并且等深度被缩放到近似微米（图 2a 和方法）。
3. 空间表达梯度 ∇d 与小脑层（等深度恒定的轮廓）垂直，并指示基因表达最大变化的空间方向。

Fig. 2: Spatial gradients learned by GASTON recapitulate the spatial organization of the mouse cerebellum.

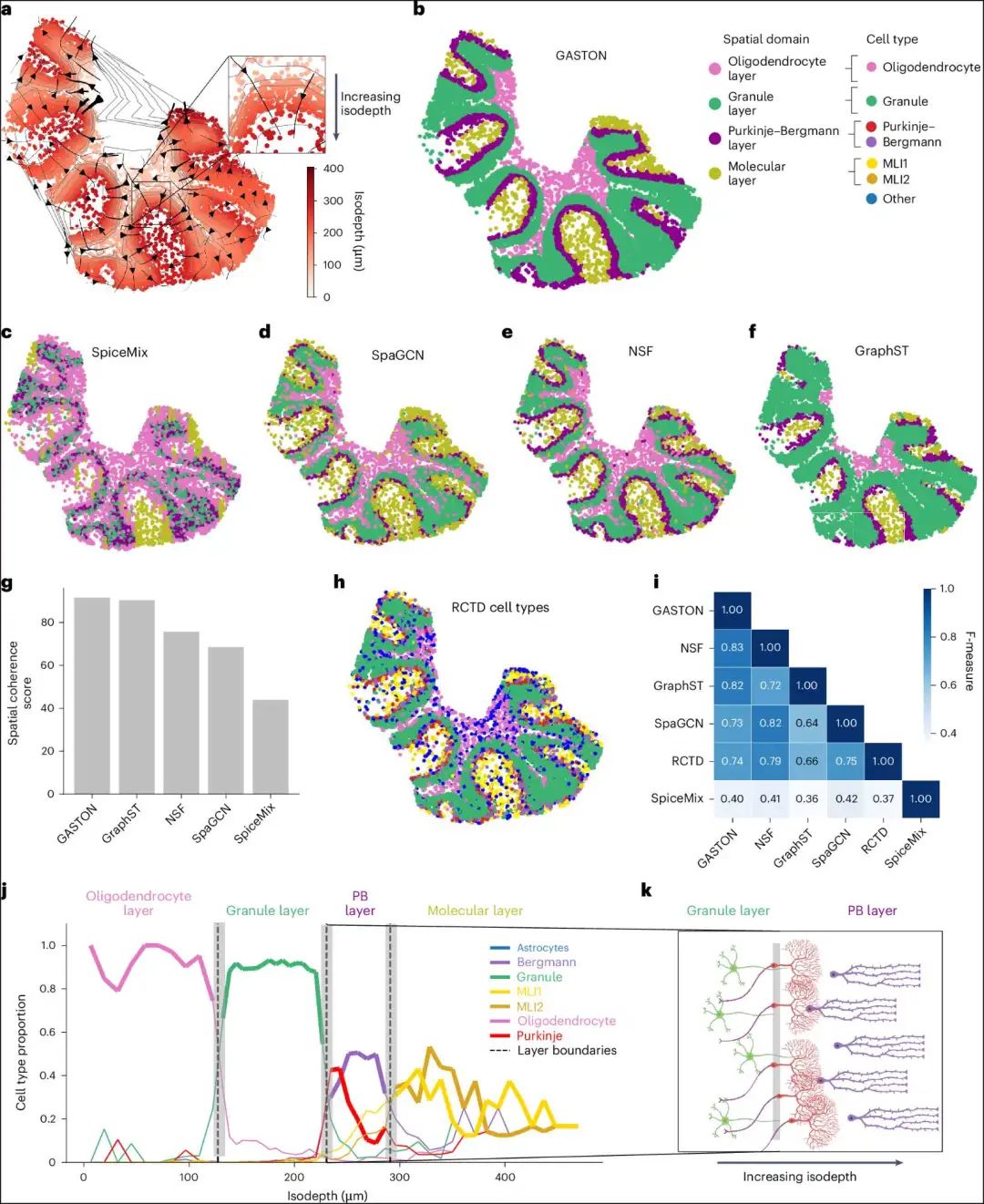
- 图片说明

◉ a，GASTON 在小鼠小脑的 Slide-SeqV2 数据上学到的等深线 d(x, y) 和空间表达梯度 ∇d，以流线形式展示。等深线按微米比例缩放，灰色曲线表示等深度轮廓。◉ b–f，使用 GASTON (b)，SpiceMix (c)，SpaGCN (d)，NSF (e) 和 GraphST (f) 识别的空间域（层）R1，…，R4。这些空间域根据域中最常见的 RCTD 细胞类型进行着色。◉ g，每种方法识别的空间域的空间一致性评分。◉ h，RCTD 识别的层特异性细胞类型。◉ i，由 GASTON、NSF、GraphST、SpaGCN 和 SpiceMix 识别的空间域与 RCTD 识别的层特异性细胞类型之间的 F 测量值。◉ j，作为等深线 d 函数的层特异性细胞类型的比例。虚线表示 GASTON 空间域的边界。◉ k，接近小脑浦金斯基-贝格曼（PB）层的颗粒细胞（绿色）、浦金斯基细胞（红色）和贝格曼细胞（紫色）在等深线上的布局。图 k 由 BioRender.com 创建。

Para_02

1. GASTON 将组织切片分为四个连续的空间域，这些域在视觉上与小脑的四个不同层一致——少突胶质细胞层、颗粒层、浦肯野-伯格曼层和分子层——这些层在先前的研究中已被识别（图2b）。
2. 我们将 GASTON 学到的空间域与四种最近的方法所识别的空间域进行了比较（图2c–f），这些方法展示了当前用于建模空间转录组数据局部空间相关性的主要方法：非负空间因子分解（NSF），它使用高斯过程模型；SpaGCN 和 GraphST，它们使用图神经网络；以及 SpiceMix，它使用隐马尔可夫随机场（HMRF）。

Para_03

1. 我们观察到，与其它方法相比，GASTON 的空间域具有更大的空间一致性（图 2g），这表明 GASTON 识别的空间域更好地符合小脑的结构几何。
2. 我们进一步将每种方法识别的空间域与原始数据发布中报告的细胞类型进行了比较（图 2h），这些数据是通过稳健的细胞类型分解（RCTD）获得的，RCTD 使用参考单细胞 RNA 测序（scRNA-seq）数据集，且不结合空间信息。
3. GASTON、SpaGCN、NSF 和 GraphST 的空间域在 RCTD 推断的细胞类型之间以及彼此之间有相似的一致性，而 SpiceMix 的空间域与 RCTD 细胞类型和其他方法的一致性较低，这一点通过 F 值（图 2i）或归一化互信息（补充图 1）进行量化。
4. 此外，GASTON、NSF 和 SpaGCN 域中每个点的比例与相应的 RCTD 细胞类型比例相似（补充图 2）。
5. 我们的结果表明，GASTON 中使用的全局空间变异模型识别出比现有方法更具空间一致性的空间域，同时保留了细胞类型信息。

Para_04

1. GASTON 的一个关键区别特征是它学习等深值 d，这为分析小脑各层内和跨层的细胞类型连续变化提供了一个坐标。
2. 这种连续变化未被上述方法或众多其他将组织切片划分为空间域的方法所建模，例如，将组织切片划分为空间域的方法未能捕捉到这种连续变化。
3. 我们发现 RCTD 细胞类型的比例随 GASTON 等深值的变化而显著变化（图 2j）。
4. 例如，少突胶质细胞和颗粒细胞在其各自层对应的等深值范围内具有较大且几乎恒定的比例。
5. 然而，在 GASTON 标记为这些层之间边界的等深值处，比例有一个急剧的转变，表明学习到的等深值 d 和空间域准确地分隔了少突胶质细胞层和颗粒细胞层。

Para_05

1. 相比之下，浦金野细胞和伯格曼胶质细胞在浦金野-伯格曼层中表现出空间变化。
2. 浦金野细胞集中在该层的起始部分（小等深），而伯格曼胶质细胞的比例在层内达到峰值，并且分布在更广泛的等深范围内。
3. 这些结果与之前的成像和显微镜研究一致，显示浦金野细胞在小脑中形成单层，即一层单细胞深度，而伯格曼胶质细胞不形成单层，而是更分散地分布在浦金野-伯格曼层中。
4. 之前的研究发现，伯格曼胶质细胞在小脑发育过程中形成单层，因此这里观察到的伯格曼胶质细胞排列可能表明其空间排列在发育后发生了变化。
5. 我们还观察到，与浦金野细胞相比，伯格曼胶质细胞更接近小脑的分子层，这也与之前关于小脑组织的研究一致。
6. 作为额外验证，即使使用从GraphST获得的细胞类型标签，所观察到的细胞类型比例模式仍然存在。

Para_06

1. 我们还将 GASTON 与两种在组织上找到连续坐标的其他方法进行了比较，即 Belayer 和 SpaceFlow。
2. Belayer 需要简单组织几何结构（无监督）或可能难以获得的复杂组织的手动注释（有监督），而 SpaceFlow 不学习空间连续测量。
3. GASTON 以无监督方式从头学习等深度，在性能上超过了 SpaceFlow 和无监督的 Belayer，并且实现了与有监督的 Belayer 相当的性能。

Para_07

1. 这些结果表明，GASTON 学习到的等深值 d 为建模复杂组织中细胞和细胞类型的空間组织提供了一种强大的计算方法。

GASTON uncovers continuous and discontinuous variation

GASTON 揭示了连续变异和不连续变异

Para_01

1. 我们接下来研究了GASTON是否能在稀疏的SRT数据中识别出具有生物学意义的基因表达空间模式，特别是在低覆盖度的Slide-SeqV2数据（每个空间位置的中位数约为500个UMI）中，这些模式可能不明显。
2. 对于每个基因g，GASTON学习一个关于等深d的分段线性函数hg(d)，该函数既模拟了在空间域内或跨空间域内的表达连续变化，也模拟了相邻空间域之间基因表达的急剧不连续性。
3. 例如，据报道Sbk1是Purkinje细胞的标记基因，在Slide-SeqV2小脑组织中，其表达非常稀疏，只有15%的所有空间位置有非零UMI计数，而在GASTON估计的Purkinje-Bergmann层中，只有2%的空间位置UMI计数超过1（图3a）。
4. 通过沿等深轮廓聚合表达值（图2a），GASTON学习了一个分段线性的Sbk1表达模式，该模式在Purkinje-Bergmann层达到峰值，并且在颗粒层中随着等深的变化表现出连续变化（图3b）。
5. 相应的二维GASTON表达函数清楚地划分了Purkinje-Bergmann层（图3c），与稀疏表达值（图3a）相比更为明显。

Fig. 3: GASTON reveals continuous and discontinuous spatial variation in gene expression in the mouse cerebellum.

- 图片说明

◉ a，Sbk1基因的表达量以对数计数每百万（logCPM）表示。◉ b，Sbk1基因的等深值与表达量的关系。线条表示GASTON学习到的分段线性函数hg(d)。◉ c，GASTON学习到的Sbk1基因表达函数f(x, y)。曲线表示等深值d的等高线。◉ d，比较GASTON和几种现有方法在标记基因识别中的表现，使用已知的小脑标记基因列表并通过AUPRC进行量化。trendsceek使用Seurat实现，C-SIDE-iso是C-SIDE，使用GASTON学习到的等深值d作为协变量。◉ e，GASTON将Frmpd4高度排名为标记基因后，其等深值与表达量的关系。◉ f，左图：Calb1基因的等深值与表达量关系，该基因在颗粒细胞中有显著的域内变异（右图），因为限制在颗粒细胞中的表达函数有较大的斜率。◉ g，左图：Secisbp2l基因的等深值与表达量关系，该基因在少突胶质细胞中有显著的域内变异（右图），因为限制在少突胶质细胞中的表达函数有较大的斜率。◉ h，Secisbp2l基因的表达量以对数计数每百万（logCPM）表示。◉ i，GASTON推断出的少突胶质细胞层中，GASTON学习到的Secisbp2l基因表达函数f(x, y)。◉ j，k，浦肯野-伯格曼层和分子层中Camk2b（j）和Camk1d（k）的等深值与表达量关系（左图），这些基因在相应层内的变异不能归因于细胞类型（右图），因为各层中最丰富的细胞类型的表达函数斜率为零。

Para_02

1. GASTON 学习到的基因表达功能在预测小脑已知标记基因方面比现有的识别空间可变基因（SVGs）或差异表达基因（DEGs）的方法有了显著改进。
2. 具体来说，与六种广泛使用的 SVG 和/或 DEG 识别方法相比，GASTON 在识别已知小脑标记基因方面的表现显著更高（精确率-召回率曲线下面积 (AUPRC) 约为 0.31；图 3d），其中基因根据 GASTON 表达函数在空间域中的方差进行排序（方法）。
3. GASTON 性能提升的主要原因是，许多现有方法仅测试每个基因的表达是否在二维空间中变化，无法区分不同类型的空间连续和非连续变化。
4. 我们重点介绍了两个由 GASTON 高度排名但其他方法未能识别的基因：Sbk1，之前已有描述，以及 Frmpd4，虽然它不是已知的标记基因，但在分子层中有高表达（图 3e），并且据报道它调节分子层中的神经元。

Para_03

1. GASTON 学习到的分段线性表达函数揭示了基因表达的不同空间模式，包括表达的不连续性——即相邻空间域之间表达的显著差异——或域内连续变化——即空间域内的分段线性函数具有较大的斜率 β（方法）。
2. GASTON 识别出 513 个具有不连续性或域内连续变化的空间可变基因（SVGs）（补充图 5a），其中包括许多先前注释的标记基因和参与神经元过程的基因（补充部分 4 和补充图 6）。
3. 大约一半的 GASTON SVGs 表现出表达的不连续性，这表明某个基因是否在特定空间域内的细胞中选择性表达或未表达（例如 Cplx2；补充图 5b），而超过 60% 的 GASTON SVGs 显示出域内连续变化（补充图 5a），这表明连续变化在小脑中相当常见。

Para_04

1. 基因表达的连续域内变异可能是由于细胞类型内的细胞状态连续体，细胞类型在组织中的比例连续变化或其他生物原因造成的。
2. 我们评估了 GASTON 识别出的域内变异是否可归因于细胞类型，或归因于每个域中注释的细胞类型（方法），以区分细胞类型内细胞状态连续体的空间成分与其他导致域内变异的生物学原因，例如细胞类型比例的空间变化。
3. 在 GASTON 报告的具有域内变异的 338 个基因中，有 217 个基因的变异可归因于细胞类型（补充图 5a）。

Para_05

1. GASTON 识别的细胞类型可归因的域内变异揭示了重要的细胞类型特异性过程，包括神经元放电和分化。
2. 例如，参与钙结合的 Calb1 表现出颗粒细胞可归因的域内变异（图 3f），为颗粒细胞中神经元放电阈值的空间梯度提供了潜在的分子解释。
3. 另一个例子是 Secisbp2l，它表现出显著的少突胶质细胞可归因的域内变异（图 3g–i）。
4. 最近的研究表明 Secisbp2l 特异性表达在分化的少突胶质细胞中，暗示少突胶质细胞的分化可能沿着等深度轴发生（图 2a）。

Para_06

1. GASTON 识别的约 35% 的域内变异不能归因于细胞类型（补充图 5a），可能由其他生物学原因引起，例如细胞类型比例的变化或细胞类型之间的相互作用。
2. 例如，Camk2b 在颗粒细胞中高表达，并在浦肯野-伯格曼层中表现出较大的域内变异（图 3j，左），这种变异不能归因于浦肯野或伯格曼细胞类型，因为 Camk2b 在浦肯野和伯格曼特异性表达函数中的斜率为零（图 3j，右）。
3. Camk2b 的域内变异可能归因于浦肯野-伯格曼层中颗粒细胞比例随等深变化而大幅减少（图 2i）。
4. 另一个例子是 Camk1d，在分子层中表现出域内变异（图 3k，左），这种变异不能归因于 MLI1 或 MLI2 神经元（图 3k，右），可能是由于其他生物学原因，如细胞间的相互作用或神经元放电。

Para_07

1. 为进一步展示大脑中的表达梯度，我们使用 GASTON 分析了 MERFISH 小鼠初级皮层数据。
2. 该数据集之前由另一研究分析过，该研究描述了 ENVI 方法，用于学习一维（1D）‘伪深度’坐标并识别连续的表达梯度。
3. 然而，与在组织切片中连续变化的 GASTON 等深线不同，我们发现 ENVI 的伪深度在整个组织中并不连续变化。
4. 因此，GASTON 识别出多个 ENVI 的伪深度坐标无法找到的空间梯度（补充部分 5 和扩展数据图 2）。

Para_08

1. 总体而言，GASTON 的连续和非连续空间变异组合模型揭示了具有生物学意义的标记基因和连续梯度，这些是现有方法无法发现的。

GASTON reveals spatial gradients in the TME

GASTON揭示了肿瘤微环境中的空间梯度

Para_01

1. 我们接下来使用 GASTON 来研究肿瘤微环境中的空间基因表达模式。
2. 肿瘤微环境与肿瘤的发展和预后密切相关，但没有空间信息很难准确量化。
3. 现有的肿瘤 SRT 数据分析仅考察肿瘤与周围基质区域之间的差异表达基因或通路。
4. 我们假设 GASTON 能够量化连续的空间变化，这可能揭示相对于肿瘤边界更为微妙的基因表达变化。

Para_02

1. 我们将 GASTON 应用于来自人类 CRC 肿瘤组织切片的 SRT 数据（图 4a），其中使用 10X Genomics Visium 平台测量了 3,900 个点位中的 36,601 条转录本的表达。
2. GASTON 识别出五个空间域（图 4b），这些域在苏木精和伊红 (H&E) 染色图像中视觉上是不同的（图 4a），包括肿瘤（域 1）、肿瘤邻近的间质区域（域 2）以及其他不直接邻近肿瘤的间质区域（域 3–5）。
3. 由于该切片没有真实的空间域注释，我们通过将其与三种 SRT 聚类工具以及原始论文中的注释进行比较来评估 GASTON 找到的空间域（补充部分 6.1 和扩展数据图 3）。

Fig. 4: GASTON identifies spatial gene expression patterns in the TME.

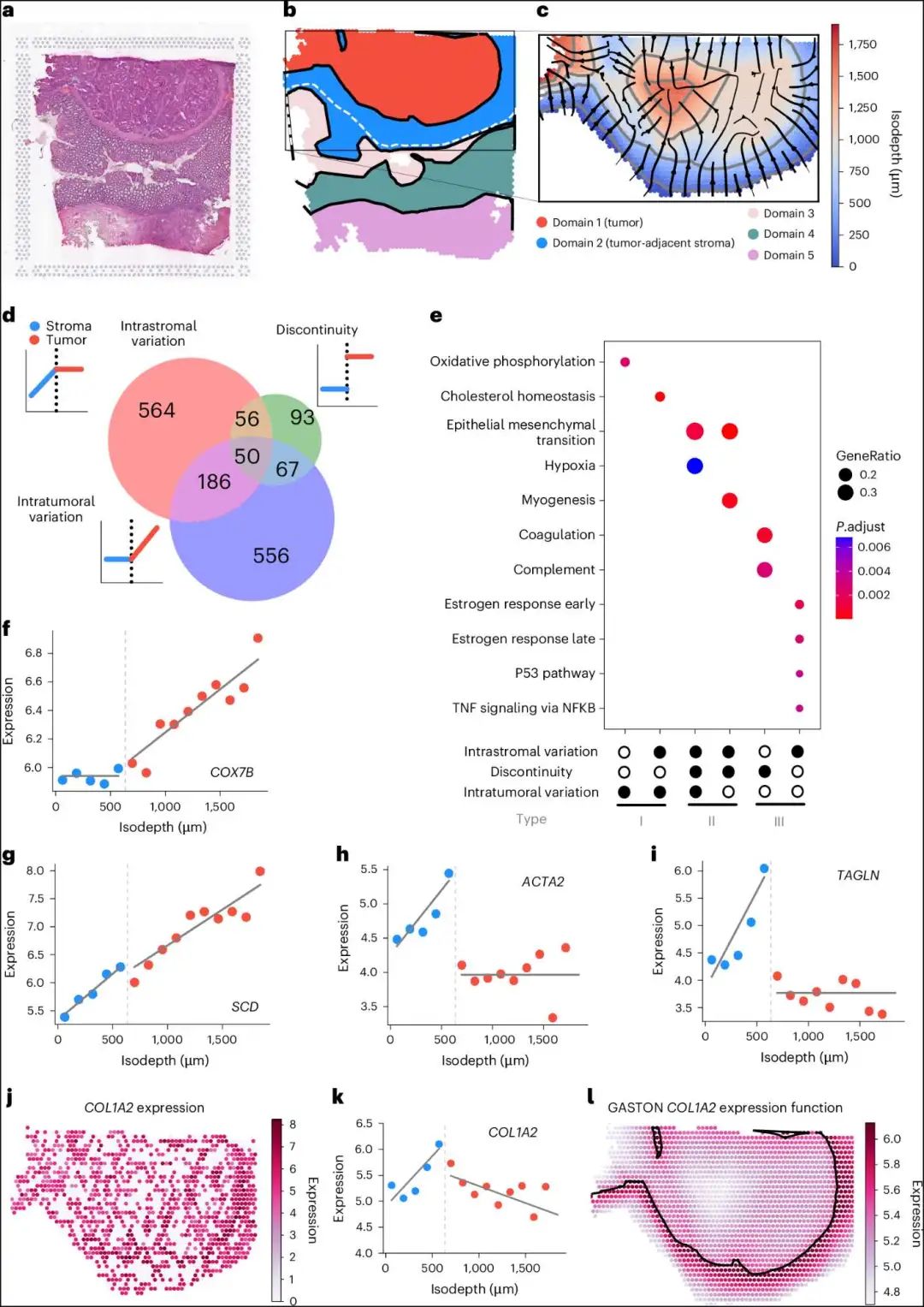
- 图片说明

◉ a，10X Genomics Visium 结直肠癌肿瘤样本的 H&E 染色。b，GASTON 学习到的空间域。根据 a 中的组织学图像，将域 1 和域 2 标记为肿瘤和肿瘤邻近的间质。c，GASTON 在肿瘤和肿瘤邻近间质域中学习到的等深度 d（缩放以近似微米）和空间梯度。d，GASTON 识别出 1,572 个空间变异基因，并将其分类为三种空间表达模式：在间质内表达变化的基因，在肿瘤-间质边界处表达不连续的基因以及在肿瘤内部表达变化的基因。e，对 d 中七种空间表达模式中的六种进行基因集富集分析，报告了标志性癌症基因集的富集情况。P 值是使用 Enrichr 实现的一侧 Fisher 精确检验计算的，并进行了多重比较调整。根据表达模式和富集的癌症通路，将空间表达模式分为三类。f-i，等深度 d 与 Type I 基因 COX47B (f) 和 SCD (g)，以及 Type II 基因 ACTA2 (h) 和 TAGLN (i) 的表达对比。j，以 logCPM 表示的 COL1A2 表达。k，Type II 基因 COL1A2 的表达与等深度的关系。l，GASTON 的 COL1A2 表达函数显示了在肿瘤-间质边界处的表达梯度。

Para_03

1. 我们通过检查每个基因的表达量作为等深变量 d 的函数，分析了 TME 的空间变化，该变量从肿瘤边界平滑变化到内部（图 4c 和补充表）。
2. GASTON 识别出肿瘤及其相邻间质域中有 1,572 个具有七种不同空间表达模式之一的空间变异基因：肿瘤内变异、肿瘤-间质边界的不连续性、间质内变异或这些模式的任意组合（图 4d）。
3. 对于七种空间基因表达模式中的六种，表现出这些空间模式的基因在癌症标志基因集中富集（P < 0.01，基因集富集分析）（图 4e）。
4. 我们将 GASTON 找到的六种富集空间基因表达模式的基因分为三种不同的类型：（1）I 型基因，其具有肿瘤内变异且表达无不连续性；（2）II 型基因，其具有间质内变异和肿瘤-间质边界的不连续性；（3）III 型基因，其具有间质内变异或肿瘤-间质边界的不连续性但没有肿瘤内变异。

Para_04

1. GASTON 识别的三种空间变异基因反映了在肿瘤微环境中发生的不同生物过程。
2. 742 个第一类基因（瘤内变异）富集于氧化磷酸化和胆固醇稳态基因集；此外，在涉及氧化磷酸化或胆固醇稳态的 42 个第一类基因中，有 39 个在肿瘤域内的斜率为正，表明从肿瘤边缘到内部表达量增加。
3. 因此，第一类基因可能指示了从肿瘤边界到内部代谢活动的梯度增加。
4. 例如，COX7B 和 SCD 是已知在缺氧条件下表达较低的第一类基因。
5. 肿瘤内部第一类基因的较高表达表明，该结直肠癌切片的内部比边界处更富氧，这与之前的临床研究一致。
6. 详细信息见补充部分 6.2。

Para_05

1. 106 型 II 基因（间质内变异和不连续性）主要描述了肿瘤边界外 EMT 基因的上调。
2. 多项研究表明，肿瘤相关间质细胞中 EMT 基因的上调与侵袭性结直肠癌亚型有关。
3. 在 EMT 通路中的 15 个型 II 基因中，有 14 个基因在肿瘤相邻间质域中的同深度表达斜率为正——即越靠近肿瘤边界表达越高——这表明该 IV 期结直肠癌肿瘤可能是一种侵袭性亚型。
4. 例如，ACTA2 和 TAGLN 被报道是结直肠癌相关成纤维细胞亚型的标志物，这些细胞具有上调的 EMT 相关基因，并且在肿瘤边界处表现出正斜率和较大的不连续性（图 4h，i 和扩展数据图 4a）。
5. 我们强调，在肿瘤边界附近 EMT 基因的上调从稀疏的 UMI 计数中并不明显，但通过 GASTON 沿同深度轮廓聚合稀疏表达测量结果得以揭示（图 4j–l）。
6. 型 III 基因主要描述免疫反应和增殖。
7. 对型 II 和 III 基因的进一步分析见补充材料第 6.2 节和补充图 7。

Para_06

1. 总体而言，GASTON 识别的空间基因表达模式表明，这种 CRC 肿瘤样本的内部生长缓慢（即细胞数量变化率低）——因为有氧代谢通过氧化磷酸化表明细胞生长和增殖缓慢——而边界则正在经历上皮-间质转化 (EMT) 进入类似干细胞的状态。
2. 我们通过显示细胞生长率随等深线（isodepth）函数而降低来验证这种生长模式（扩展数据图 4b）。
3. 肿瘤内部和边界的这些特征表明这是一个晚期、血管化的原发性肿瘤，具有完全转移性的边缘，这一描述与肿瘤的临床信息相符。

Para_07

1. 我们还使用 GASTON 分析了通过 10X Genomics Xenium 平台测量的人类乳腺癌肿瘤中不典型导管增生区域的 TME（图 5a）。
2. GASTON 学习了一个从增生区域外向内连续变化的等深度（图 5b），并识别出四个空间域：外侵袭性肿瘤、外间质、中间免疫域和原位导管癌域（图 5c）。
3. GASTON 学习到的等深度量化了 TME 中肿瘤浸润淋巴细胞的空间位置（图 5d），并揭示了由肿瘤浸润淋巴细胞引起的免疫细胞分化和相互作用的表达梯度（图 5e）。
4. 详情见补充部分 7。

Fig. 5: Spatial gradients of gene expression and cell type in a 10X Genomics Xenium breast cancer dataset.

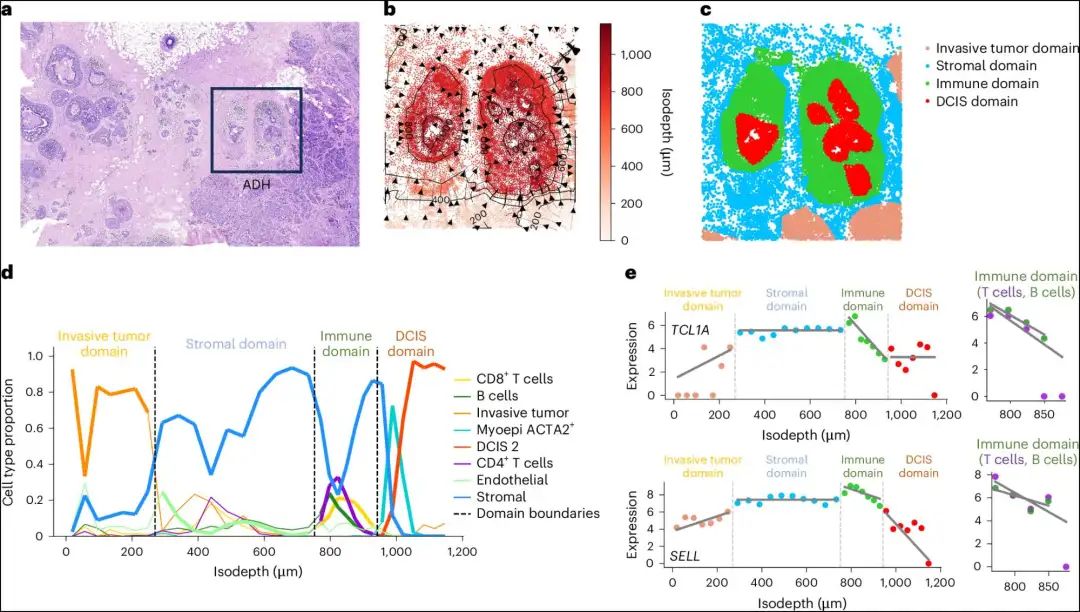
- 图片说明

◉ a，H&E染色的乳腺癌图像，其中不典型导管增生（ADH）区域如参考文献13中标记所示。◉ b，GASTON学习到的等深度（按比例缩放到近似微米）和空间梯度。◉ c，GASTON根据域中最主要的细胞类型标记出的空间域。◉ d，作为等深度d函数的细胞类型比例。虚线表示由GASTON识别的空间域边界。◉ e，等深度与TCL1A（上）和SELL（下）表达的关系。TCL1A在免疫域中表现出T细胞和B细胞可归因的变化，而SELL表现出T细胞可归因的变化。

Para_08

1. 我们的分析展示了 GASTON 学到的基因表达拓扑结构如何使肿瘤微环境的空间和分子组织特征得以描述。

Gene expression topography of sparse Stereo-seq data

稀疏 Stereo-seq 数据的基因表达拓扑结构

Mouse olfactory bulb

小鼠嗅球

Para_01

1. 我们使用 GASTON 分析了来自小鼠嗅球的 Stereo-seq 数据，其中包含 9,825 个细胞中的 27,106 个转录本的表达。
2. Stereo-seq 数据非常稀疏，每个位置的中位 UMI 小于 350。
3. 同时，嗅球具有由多个同心层组成的径向几何结构，提供了可能有助于克服严重数据稀疏性的空间约束。

Fig. 6: GASTON reveals variation in cell types and gene expression in the mouse olfactory bulb.

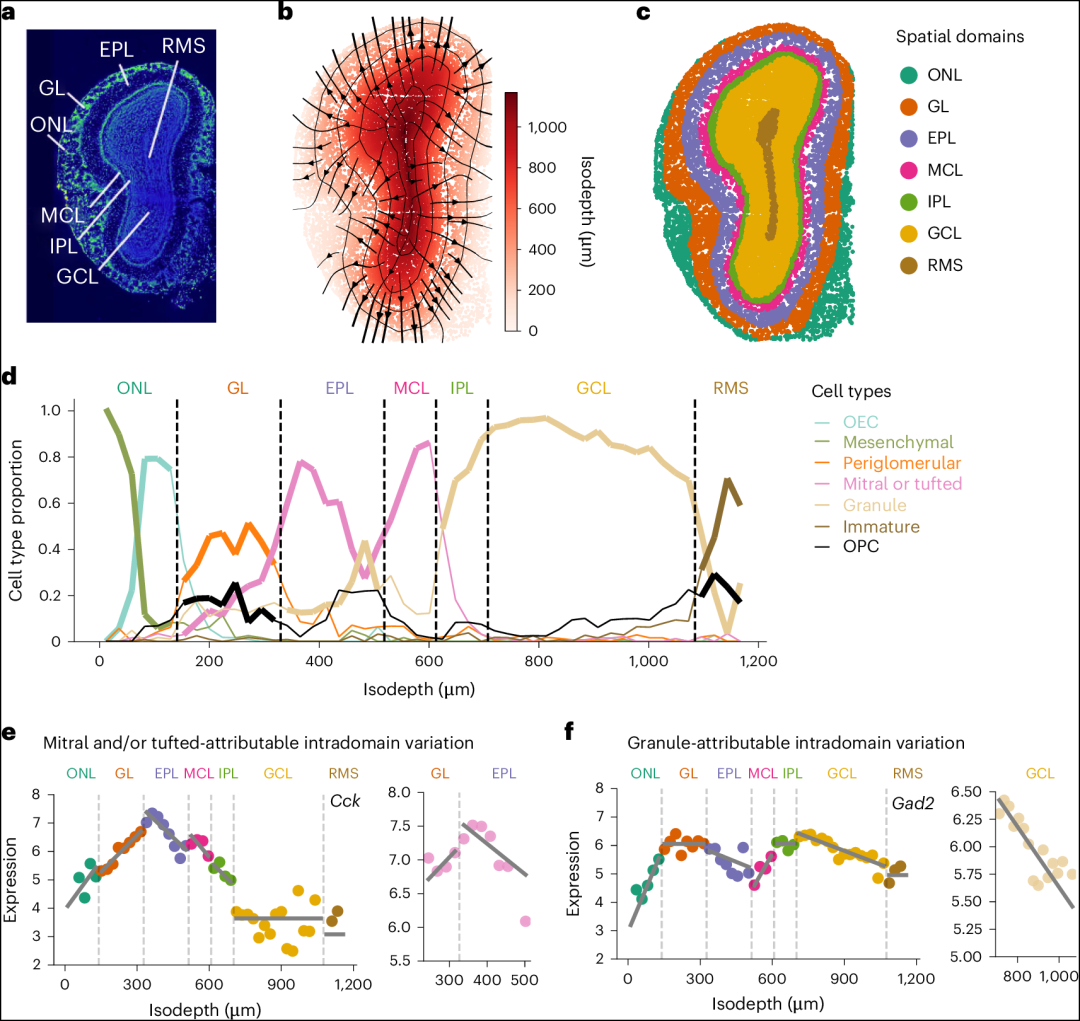
- 图片说明

◉ a，来自小鼠嗅球的4,6-二氨基-2-苯基吲哚染色图像，该图复制自参考文献。b，GASTON 学习到的等深度 d 和（负）空间梯度 −∇d（以流线形式显示）。等深度的比例约为微米级，曲线表示恒定等深度 d 的轮廓。c，GASTON 学习到并基于 a 中注释标记的空间域。MCL 表示僧帽细胞层；IPL 表示内部丛状层；OEC 表示嗅鞘细胞；OPC 表示少突胶质前体细胞。d，作为等深度 d 函数的细胞类型比例。虚线表示 GASTON 识别出的空间域边界。每个空间域中最丰富的细胞类型被突出显示。e，左：在球状层（GL）和外部丛状层（EPL）中，Cck 的等深度与表达关系，该基因具有由僧帽细胞和/或簇状细胞引起的域内变异（右）。f，左：在颗粒细胞层（GCL）中，Gad2 的等深度与表达关系，该基因具有由颗粒细胞引起的域内变异（右）。

Para_02

1. GASTON 几乎完美地学习了嗅球的径向几何结构，其中等深线 d 提供了一张反映嗅球几何结构的地形图（图 6b）。
2. 利用学到的等深线，GASTON 将组织划分为七个连续的空间域（图 6c），这些域在视觉上对应于嗅球的七个不同层（图 6a）。
3. 相比之下，SpaGCN 和 NSF 识别出的空间域不连贯，无法解析最内层的组织（扩展数据图 5 和补充部分 3）。

Para_03

1. 嗅球是大脑中两个发生成年神经发生区域之一，未成熟神经元从脑室迁移流（RMS，大等深）向外迁移到最外层的嗅神经层（ONL，小等深）。
2. 因此，在这种组织中，GASTON 等深 d 提供了嗅球中潜能的测量，而负梯度 −∇d 显示了神经元成熟和迁移的空间轨迹。

Para_04

1. GASTON 学习到的等深信息揭示了每层组织中细胞类型的精确空间排列（图 6d），这在文献中尚未完全描述。
2. 例如，虽然先前的研究发现间充质细胞和嗅鞘细胞都位于最外层的 ONL 中，但 GASTON 识别出这两种细胞类型在 ONL 中有不同的空间排列：间充质细胞集中在该层的外缘（等深 d < 50），而嗅鞘细胞在较大的等深处达到峰值（d ≈ 85）并且在整个 ONL 中分布更为弥散，这一发现与之前的发育研究结果一致。

Para_05

1. 等深度 d 区分了具有相似基因表达谱的不同细胞类型或细胞状态。
2. 例如，尽管在单细胞参考数据集中，由于它们的基因表达谱相似，嗅球细胞和簇状细胞被归为一组，GASTON 显示出嗅球细胞和/或簇状细胞的比例在两个不同层中分别在两个不同的等深度值处达到峰值：在嗅小球层和/或外侧丛状层（EPL）中的 d 约为 350 和在嗅球细胞层中的 d 约为 600（图 6d）。
3. 基于之前的生物学研究，我们假设等深度 d 约为 350 处的嗅球细胞和/或簇状细胞是簇状细胞，而等深度 d 约为 600 处的嗅球细胞和/或簇状细胞是嗅球细胞（补充部分 8）。
4. GASTON 还识别出几个颗粒细胞的亚群，这些亚群可能对应于之前研究过的、形态上不同的颗粒细胞状态（补充部分 8）。
5. 值得注意的是，使用基于 scRNA-seq 的一维坐标无法获得这些发现（补充部分 3 和扩展数据图 5）。

Para_06

1. GASTON 识别出 704 个基因，这些基因在表达上存在不连续性或较大的域内变异（补充图 8 和补充表）。
2. 这些基因区分了嗅球中不同的细胞类型和状态，并揭示了潜在的分子机制，解释了一些生物学现象。
3. 例如，Cck 是某些簇状细胞亚型的标记基因，在小球层/EPL 中表现出与米特细胞和/或簇状细胞相关的变异（图 6e）；
4. Gad2 是 GABA 能系统中神经元的标记基因，在颗粒细胞层中表现出与颗粒细胞相关的变异；
5. Dcx 是 RMS 中未成熟神经元的标记基因，在 RMS 中表现出与细胞类型无关的域内变异（扩展数据图 6）。
6. 详情见补充部分 8。

Mouse embryo

小鼠胚胎

Discussion

Para_01

1. 组织内空间基因表达变化的精确模型对于确定细胞类型的空间组织以及定义调节细胞在空间生态位中状态的分化和细胞间通信过程至关重要。
2. 基因表达的空间变化包括在组织的不同空间域之间的不连续变化，以及由于细胞状态变化或其他原因导致的空间域内部和之间的连续变化。
3. 虽然已经开发了许多计算方法来识别空间域，但很少有方法能够同时识别空间域并建模域内的连续变化。
4. 与此同时，虽然许多方法旨在推断转录组空间中的连续变化（如轨迹推断或伪时间方法），但现有方法在建模物理空间中的连续变化时面临挑战。

Para_02

1. 在这项工作中，我们引入了等深度坐标，该坐标模型化了组织内部空间域的排列以及每个域内空间位置的相对位置，从而能够量化连续和不连续的空间变化。
2. 等深度坐标为组织切片提供了地形图，类似于地球表面地图中的海拔高度，并提供了一个全局的空间基因表达模型。
3. 就像人们可以在两座不同的山上攀登到相同的海拔一样，等深度坐标也可以在相同的空间域内两个空间分离的位置取相同的值，例如小鼠小脑的浦肯野-伯格曼层（图2b）。
4. 相比之下，大多数现有的空间转录组学方法仅模型化空间相邻位置之间的局部空间相关性。

Para_03

1. 我们的工作还引入了肿瘤分类的新轴，其中肿瘤可以通过不同肿瘤过程在空间梯度上的变化进一步表征；例如，某些肿瘤可能在向肿瘤内部的方向上表现出有氧代谢的增加梯度（例如，图4），而其他肿瘤则可能表现出减少的梯度。
2. 此外，GASTON 学习到的空间梯度可以揭示转移性迁移的空间轨迹（例如，边缘化现象），类似于 GASTON 在嗅球中的空间梯度展示了神经元迁移的空间轨迹（图6b）。

Para_04

1. 我们注意到，GASTON 当前的等深线推导依赖于两个简化假设，这些假设在特定应用中可能需要调整。
2. 首先，我们假设所有（空间变化的）基因共享相同的空间梯度向量场，而 GASTON 不会自动找到多个空间变化方向。
3. 对于这些情况，使用受限的基因集或组织切片的较小区域来学习等深线可能是合适的；例如，可以将 GASTON 应用于从标准 SRT 或单细胞聚类算法获得的基因集或空间域。
4. 其次，我们假设空间梯度向量场是保守的，这意味着它在空间中不会‘旋转’。
5. 尽管我们尚未发现任何违反这一假设的生物学实例，但 GASTON 可能不适用于这种假设被违反的组织切片。

Para_05

1. 我们设想，等深度的数学框架和 GASTON 算法的简单性和通用性可以很容易地在多个方向上扩展，包括用更复杂的分段函数替换分段线性函数，或扩展到其他分子模式，例如染色质可及性或蛋白质丰度。
2. 此外，GASTON 识别出许多空间基因表达梯度的例子，进一步研究这些梯度的调控原因及其下游效应是值得的。

Para_06

1. GASTON 计算的地形图和基因表达功能提供了一个通用框架，用于分析空间测序数据中的连续和不连续空间变异。

Methods

Modeling gene expression and spatial gradients

建模基因表达和空间梯度

Para_01

1. 我们推导了一个用于空间域和基因表达梯度的SRT数据模型。
2. SRT技术测量组织切片中G个基因的表达，我们用一个基因表达函数f：T→R^G来建模，其中T⊆R^2。
3. 向量f(x, y) = (f_1(x, y), …, f_G(x, y))^⊤给出了组织切片T中每个位置(x, y)处每个基因的（归一化）表达量，其中第g个分量函数f_g: R^2→R描述了单个基因g的表达。
4. 例如，一个在组织切片T中表达恒定的基因g具有常数表达函数f_g(x, y) = c，而一个在区域R⊆T中差异表达的基因可能具有表达函数f_g(x, y) = c×1_{(x, y)∈R"} + c'×1_{(x, y)∉R"}。

Para_02

1. 我们将每个表达函数 fg 建模为分段连续函数。
2. 分段连续函数可以模拟基因表达中的连续空间变化，同时允许由于细胞类型组成或其他因素的急剧变化而导致的表达不连续性。
3. 我们假设所有基因的表达函数 fg 具有相同的分段，因此每个表达函数 fg 的形式为： 错误！！！ - 待补充

Para_04

1. 空间梯度描述了基因表达在二维组织切片 T 中的变化情况。对于单个基因 g，空间梯度由表达函数 fg 的梯度 ∇fg 给出。
2. 更一般地，基因表达函数 f 的雅可比矩阵 J(f) = [∇f1 ... ∇fG]^T ∈ R^(G×2) 的各行给出了每个基因在每个空间位置 (x, y) ∈ T 处的个体空间梯度。
3. 注意，雅可比矩阵 J(f) 的秩最多为二。

Para_05

1. 从单个组织切片的 SRT 数据中估计每个基因 g 的空间梯度 ∇fg 是困难的，因为数据的空间分辨率有限且测序覆盖率有限（例如，稀疏性）。
2. 为了避免过拟合，我们对空间梯度的结构做出一些假设。
3. 具体来说，我们假设雅可比矩阵 J(f) 在每个空间位置 (x, y) ∈ T 上的秩为一，即雅可比矩阵 J(f)(x, y) 的行 ∇fg(x, y) 在每个空间位置 (x, y) ∈ T 上是线性相关的。
4. 这一假设的动机在于观察到空间表达梯度往往具有相关性；例如，在大脑和肝脏中，许多基因被观察到沿相同的轴具有表达梯度。
5. 有关这一假设的实证验证，请参阅补充部分 10。

Para_06

1. 在这一假设下，对于每个空间位置 (x, y) ∈ T，存在一个向量 v(x, y) ∈ R²，使得每个基因 g 的梯度向量 ∇fg(x, y) 是向量 v(x, y) 的标量倍数：

Para_07

1. 其中 βg(x, y): R² → R 是标量函数，v(x, y) 是我们称为空间梯度矢量场的矢量场。由于表达函数 f 是分段连续的，每个表达函数 fg 的梯度 ∇fg 也是分段连续的，因此我们可以将方程 (3) 重写为
2. 这是关于表达函数 f 的描述，它分段连续，使得每个表达函数 fg 的梯度 ∇fg 也分段连续，从而可以对方程 (3) 进行重写。

Conservative vector fields and piecewise linear functions

保守向量场和分段线性函数

Para_01

1. 公式（4）提供了一个在雅可比矩阵 J(f) 满足秩为一假设下的空间梯度 ∇fg 的一般模型。然而，在实际中，从 SRT 数据估计公式（4）的参数仍然很困难，因为我们观察到的不是表达梯度 ∇fg，而只是表达值 fg。为了推导出表达函数 fg 的模型并尽量减少过拟合，我们对空间梯度向量场 v、空间域 Rp 和标量函数 βg(x, y) 做了三个简化假设。

Para_02

1. 首先，我们假设空间梯度向量场 v 是连续可微标量函数 d 的梯度，即 v = ∇d，其中 d: R² → R。
2. 我们将 d 称为组织切片 T 的等深线。
3. 等深线 d 描述了组织切片 T 的‘地形’，类似于地理区域的地形图中的高程。
4. 由标量函数 d 导出的向量场 v 被称为保守向量场，而标量函数 d 被称为势函数，因为它测量了空间中不同位置的势能，例如重力势函数或电势函数。
5. 在我们的设定中，标量函数 d 测量了组织切片 T 中不同位置的‘基因表达势’。
6. 向量场 v 为保守向量场意味着 v 的旋度处处为 0，也就是说，组织中没有向量场 v ‘旋转’的区域。
7. 我们强调，由于等深线 d 是连续可微的，因此空间梯度向量场 v = ∇d 在整个组织切片 T 上是连续的，并且不特定于某个域。

Para_03

1. 其次，我们将每个空间域 Rp 建模为等深度 d 的水平集的并集。具体来说，我们假设每个空间域 Rp = ((x, y): bp−1 < d(x, y) ≤ bp) 等于等深度 d(x, y) 在区间 (bp−1, bp] 内的空间位置 (x, y) 的集合，对于某些实数 −∞ = b0 < b1 < ⋯ < bQ−1 < bQ = ∞。这确保了空间域 Rp 不会相交，并导致表达函数 fg 具有特别简单的形式，如下所示。

Para_04

1. 第三，我们假设标量函数 βg(x, y) 在每个空间域 Rp 内是常数；也就是说，标量函数 βg(x, y) = ∑_{p=1}^{Q"} βg,p 1_{(x,y) ∈ Rp"} 是分段常数。

Para_05

1. 在这些假设下，方程（4）中的空间梯度∇fg相等

Para_06

1. 对公式(5)的两边进行积分，得到基因表达函数fg的闭合形式如下：

Para_07

1. 对于某些常数 αg,p 和 βg,p。将公式 (6) 应用于所有基因 g = 1, …, G，可以得到基因表达向量 f = (f1, …, fG) 的如下表达式： 错误！！！ - 待补充

Para_09

1. 因此，在我们的模型中，空间位置 (x, y) ∈ T 处的基因表达函数 f(x, y) 由等深线 d 和分段线性函数 h(d(x, y)) 组成，其中 h 是一个从实数域映射到 G 维实数空间的分段线性函数，具有 Q 段和断点 b1, …, bQ−1。
2. 向量αp和βp分别是函数h在所有G个基因的第p段的y轴截距和斜率。我们称函数h(w)为一维（1D）表达函数，因为它是一个单一变量w（即等深）的函数，这与基因表达函数f(x, y)不同，后者是两个空间变量x和y的函数。

Long-range spatial correlations and pooling

长程空间相关性和池化

Para_01

1. 将基因表达建模为等深的单变量函数的主要优势在于能够结合来自不同空间位置的基因表达测量，从而克服当前 SRT 技术的稀疏性。
2. 具体来说，所有具有相同等深 d 的空间位置都具有相同的基因表达值 h(d)，因此 h(d) 的估计可以使用等深轮廓上的所有位置。
3. 该轮廓可能贯穿整个组织切片，并且不必是连续的曲线（例如，图 2a）。
4. 因此，等深模型描述了长程空间相关性，这与许多现有的用于分析 SRT 数据的算法形成对比，这些算法仅结合相邻点之间的局部相关性，例如使用隐马尔可夫随机场或高斯过程。
5. 此外，等深模型允许在组织切片中跨空间分离区域‘汇集’信息。

Para_02

1. 等深模型显著推广了分层组织和相对深度的模型，该模型在参考文献中将空间域 R1, …, RQ 限制为满足严格拓扑约束的层次结构。
2. 参考文献中的拓扑约束要求不被许多组织所满足，导致推断出明显不准确的空间域，包括论文中分析的许多组织切片（补充图 9）。
3. 相比之下，在这项工作中，我们对空间域 R1, …, RQ 施加的拓扑约束较少，并且我们直接从 SRT 数据中学习空间域和等深信息，无需任何先前知识，如下所述。

Maximum likelihood estimation

最大似然估计

错误！！！ - 待补充 错误！！！ - 待补充 错误！！！ - 待补充

Para_04

1. STP极大地推广了我们之前工作中假设的L层问题，之前的工作假设等深度d由分段保角映射给出，其中各段要么由直线界定，要么由对空间域Rp形状的先前知识确定。

Para_05

1. STP 是一个具有挑战性的非凸优化问题，涉及连续可微和分段连续函数的空间。
2. 我们使用深度学习来解决这个优化问题。
3. 根据通用近似定理，可以用神经网络逼近连续函数 d。
4. 此外，即使分段连续函数也可以通过神经网络很好地逼近，尽管识别函数的各个分段可能在计算上是不可行的。
5. 因此，我们采用两步法来解决 STP，首先学习等深 d，然后学习分段线性表达函数 h。 错误！！！ - 待补充

Para_07

1. 修改后的问题在公式 (10) 中对于大多数神经网络架构仍然是一个非凸优化问题。然而，通过使用神经网络参数化这些参数，我们利用了现代深度学习框架可以对此类问题进行近似且高效求解的事实。 错误！！！ - 待补充 错误！！！ - 待补充 错误！！！ - 待补充
2. 当只有一个基因（G = 1）时，方程（11）中的最大似然问题是一个分段回归问题，这是一个经典的统计学问题，可以通过动态规划解决，正如我们在之前的工作中所描述的那样。
3. 对于 G > 1 的基因，我们使用参考文献中推导出的分段回归动态规划变体来求解方程（11）。
4. 我们强调，我们在步骤1和步骤2中分别以无监督的方式解决公式(10)和(11)中的优化问题，因为我们没有使用超出SRT数据(A, S)的任何信息。

Training and implementation

培训与实施

Para_01

1. 上述算法可以通过不同的概率分布实现，即基因表达值 ai,g 的概率分布为 P(ai,g | fg(xi, yi)) = P(ai,g | hg(d(xi, yi)))。
2. 根据之前的研究，我们使用泊松分布来建模 UMI 计数 ai,g，形式为 ai,g 独立同分布于 Pois(Ui · exp(fg(xi, yi)))，其中 Ui 是位置 i 处的总 UMI 计数。

Para_02

1. 实际上，虽然可以使用所有或选定的基因表达值，但为了效率，我们并不直接使用观测到的基因表达值来求解 STP（公式（9））。
2. 相反，我们计算广义线性模型主成分（GLM-PCs），并使用前 2Q 个 GLM-PCs 在高斯误差模型下求解公式（10）。
3. 这种简化是合理的，因为在我们之前的工作中，我们已经证明对于从泊松表达模型和分段线性表达函数 h 生成的 SRT 数据（A, S），转录计数矩阵 A 的前 2Q 个 GLM-PCs 也是分段线性的，并且带有高斯噪声。
4. 经验上，我们也观察到（扩展数据图 8），前 2Q 个 GLM-PCs 大致是分段线性的，其中的片段对应于空间域，而 GLM-PCs 中的不连续点位于域边界。 错误！！！ - 待补充

Para_04

1. 我们使用具有两个隐藏层、每层大小为20的神经网络 dθ 和 h'_{θ'} 来求解公式 (12) 中的优化问题，并使用 Adam 优化器进行10,000次迭代训练。
2. 由于公式 (10) 的非凸性，我们使用30个随机初始化，并选择具有最大似然值的解。
3. 请注意，公式 (12) 可以在不需知道方差参数 σ² 的情况下求解。
4. 对于结直肠癌肿瘤（参见‘GASTON揭示了TME中的空间梯度’部分），为了从组织学图像中捕捉空间变化，我们使用前 (2Q − 3) 个 GLM-PCs 以及从 H&E 染色图像中提取的平均红、绿和蓝值，从而在公式 (12) 中得到 (2Q − 3) + 3 = 2Q 个总特征。 错误！！！ - 待补充

Para_06

1. 我们使用泊松表达模型来描述UMI计数ai,g。我们使用sklearn包中的泊松回归来解决等式（13）中的优化问题，针对每个单独的基因g和空间域Rp。因此，解决等式（13）相当于解决G × Q个泊松回归问题，每个基因和空间域的组合对应一个问题。

Para_07

1. 为防止过拟合，我们随后对每个基因 g 在域 Rp 中的斜率 βg,p 是否为零进行假设检验，即我们检验这些假设

Para_08

1. 对于每个基因 g 和域 Rp，我们根据泊松表达模型计算零假设和备择假设的对数似然比（LLR），并假设 2 × LLR 服从 χ2 分布来估计 P 值，这在渐近情况下由威尔克斯定理成立。
2. 如果 P 值小于 0.1，我们将斜率 βg,p 设置为零。

Para_09

1. 我们仅对基因 g 估计一维表达函数 hg，这些基因的 UMI 计数总和至少为 K，其中小脑和嗅球的 K = 500（见‘GASTON 再现了小鼠小脑的空间组织’和‘GASTON 揭示连续和不连续变异’部分），CRC 肿瘤的 K = 1,000（见‘GASTON 揭示肿瘤微环境中的空间梯度’部分）。
2. 这些 K 的选择结果大约有 2,000 到 5,000 个基因，我们对其估计表达函数。
3. 此外，对于 Slide-SeqV2 和 Stereo-Seq 应用中 UMI 计数稀疏的情况，我们仅在域 Rp 中估计斜率 βg,p，如果基因 g 在域 Rp 中至少有 T 个非零 UMI 计数的位置。
4. 我们使用小脑的 T = 75 和嗅球的 T = 20，这大约是最小域中空间位置数量的 10%。
5. 我们观察到（补充图10和补充表1），每个域 Rp 中有15–40%的基因具有非恒定斜率，即在域内存在空间变化的表达（GASTON P < 0.05）。
6. 相比之下，我们强调现有的大多数 SRT 算法假设基因表达在空间域内是恒定的，并没有明确建模空间域内的连续基因表达梯度。
7. 例如，HMRFs 假设基因表达在空间域条件下是恒定的，而 SpaGCN 和其他图卷积网络（GCNs）最小化空间域内每个点与域中心之间的表达距离（即，空间域内的平均表达），这隐含地假设基因表达在域内是恒定的。
8. 关于模型选择，对于本文中的所有分析（除了一项），我们通过在对数似然图中识别拐点来确定空间域的数量 Q，这是聚类中的标准方法。
9. 我们使用 Kneedle 算法进行此模型选择，该算法实现在 kneed Python 包中。
10. 例外是嗅球（参见‘GASTON 揭示连续和不连续的变化’部分），基于先前的知识，我们知道嗅球包含七个层次，因此我们使用 Q = 7 个域（而不是 Kneedle 给出的 Q = 8）（图 6a）。
11. 关于运行时间，对于本文分析的数据集，计算顶级广义线性模型主成分（GLM-PCs）大约需要30到40分钟，而求解方程（12）和（13）每个大约需要5分钟（在CPU上）。
12. 可以通过使用较少的基因或较大的收敛阈值来减少广义线性模型主成分分析（GLM-PCA）的运行时间。
13. 或者，可以使用泊松回归或负二项式回归的解析皮尔逊残差的顶级主成分来求解方程（12）。
14. 例如，在小脑分析中（章节‘GASTON重现了小鼠小脑的空间组织’和‘GASTON揭示了连续和不连续的变化’），使用解析皮尔逊残差的主成分得到的等深图与使用顶级广义线性模型主成分（GLM-PCs）得到的等深图高度相关（皮尔逊相关系数为0.88）。

Quantifying spatial variation in gene expression

量化基因表达的空间变异

错误！！！ - 待补充

Para_02

1. 对于不连续表达，设 δg,p 为函数 hg 在断点 bp 处的不连续性，即 δg,p = (αg,p+1 + βg,p+1bp) − (αg,p + βg,pbp)。一个大的（绝对值）不连续性 ∣δg,p∣ 表示基因 g 在空间域 Rp 和 Rp+1 边界处的表达存在显著的不连续变化。 错误！！！ - 待补充 错误！！！ - 待补充

Attributing continuous variation in expression to cell types

将表达的连续变异归因于细胞类型

Para_01

1. 域内表达变异——即，在分段线性拟合中，域 Rp 的斜率 βg,p 较大——可能是由于细胞类型内的表达变异、细胞类型比例的变化或其他潜在未知的生物学原因引起的。
2. 为了说明，考虑单个基因 g 的一维表达函数 h(w) = hg(w)。
3. 给定细胞类型 c = 1, …, C，函数 h(w) 表示为 错误！！！ - 待补充 错误！！！ - 待补充 错误！！！ - 待补充

Para_05

1. 其中，αc,p = (αc,p,g)g = 1, …, G 和 βc,p = (βc,p,g)g = 1, …, G 分别是细胞类型 c 特异的截距和斜率，在空间域 Rp 中的细胞类型 c 特异表达函数 hc = (hc,1, …, hc,G)。 错误！！！ - 待补充 错误！！！ - 待补充

Para_08

1. 为了评估域内变异是否可归因于细胞类型，我们将特定细胞类型的斜率βc,g,p与不考虑细胞类型的斜率βg,p进行比较，后者是从不考虑细胞类型的表达函数h(w)（公式（8））中得出的。
2. 具体来说，我们将参数αp=(αg,p)g∈G和βp=(βg,p)g∈G分别称为不考虑细胞类型的y轴截距和斜率。
3. 如果特定细胞类型的斜率βc,g,p接近或大于不考虑细胞类型的斜率βg,p，则连续表达变异——即βg,p的较大值——归因于细胞类型c。
4. 相反，如果特定细胞类型的斜率βc,g,p远小于不考虑细胞类型的斜率βg,p，则连续表达变异不可归因于细胞类型c。 错误！！！ - 待补充
5. 我们强调，GASTON 仅能识别那些其域内变异可归因于空间域中主导细胞类型的基因，无法完全解析这种域内变异的不同可能生物学原因。
6. 如果一个基因表现出的域内表达变异不能归因于某种细胞类型，则这种变异可能是由多种原因引起的，包括非主导细胞类型、细胞类型比例的变化、两种细胞类型之间的相互作用或其他生物学原因。
7. 在没有额外数据的情况下，很难区分这些不同的解释。

Visualization

可视化

Scaling isodepth to physical distance

将等深线缩放到物理距离

Para_01

1. GASTON 中的神经网络学习了一个在组织切片 T 上平滑变化的等深度 d(x, y)；然而，所学等深度 d(x, y) 的缩放是任意的。
2. 为了提高神经网络所学等深度 d(x, y) 的可解释性，我们在每个空间域内对等深度进行缩放，以反映域内的近似物理距离。
3. 简而言之，我们推导出每个空间域 Rp 的‘平均宽度’的估计值 γp（以微米为单位），并对每个空间域中的等深度 d(x, y) 进行线性变换，使得域 Rp 内的等深度值范围为 γp。 错误！！！ - 待补充 错误！！！ - 待补充 错误！！！ - 待补充

Para_05

1. 我们通过计算每个空间域 Rp 的两个边界之间的中位物理距离来估计其平均宽度 γp。
2. 具体来说，令 Γlower = {(xi, yi) ∈ Rp: bp−1 < d(xi, yi) < bp−1 + ϵ} 和令 Γupper = {(xi, yi) ∈ Rp: bp - ϵ' < d(xi, yi) < bp"} 分别为空间域 Rp 下边界和上边界曲线上的空间位置集合。
3. 我们将 γp 设定为 Γlower 中每个点 (x, y) 与其在 Γupper 中最近点之间的中位距离。
4. 我们选择 ϵ 和 ϵ' 使得 Γlower 和 Γupper 在视觉上对应于空间域的边界。

Para_06

1. 对于 10X Genomics Visium 数据，我们将每个平均宽度 γp 乘以 100，因为 10X Visium 玻片上相邻点中心之间的物理距离为 100 微米。
2. 对于 Slide-seqV2 数据，我们将每个平均宽度 γp 乘以 64/100，因为在 Slide-SeqV2 显微镜图像中相距 100 像素的两个珠子的物理距离大约为 64 微米。

Visualizing 1D expression functions

可视化一维表达函数

错误！！！ - 待补充 错误！！！ - 待补充

Para_03

1. 我们强调，零和非零表达值之间存在较大的视觉差异，这是由于使用对数池化 CPM 进行可视化所致，并不是 GASTON 的固有特性。这是因为我们在拟合 GASTON 时使用的是离散的 UMI 计数值，而不是对数 CPM 值，这种做法在单细胞文献中通常被推荐。
2. 此外，零和非零表达值之间的显著差异仅在可视化那些在空间域中表达为零的基因时才会观察到：例如，在少突胶质细胞和分子层内部表达为零的 Sbk1 基因（图 2a）。

Marker gene analysis

标志基因分析

错误！！！ - 待补充

Para_02

1. 我们将 GASTON 与六种现有的方法进行了比较，这些方法用于识别空间变异基因或差异表达基因：HotSpot、trendsceek、SpatialDE、SPARK-X、C-SIDE 和 SpaGCN，它们的 AUPRC 范围从 0.07 到 0.25。

Para_03

1. 为了进一步证明 GASTON 学习到的等深值 d 的实用性，我们使用等深值作为 C-SIDE 的协变量，C-SIDE 用于从 SRT 数据中识别特定细胞类型的差异表达基因。
2. 这种变化的 C-SIDE，我们称之为 C-SIDE-iso，与原始 C-SIDE 相比，识别出的差异表达基因集有显著不同，两者识别的差异表达基因仅有 10% 的重叠。
3. 在标记基因识别方面，C-SIDE-iso 的表现优于原始 C-SIDE（图 3c），这证明了等深值 d 的优势。
4. 然而，与 GASTON 不同，C-SIDE-iso 无法识别空间域，因此无法测试不同空间域之间的表达变化，因此在标记基因识别方面，C-SIDE-iso 的表现低于 GASTON（图 3c）。

Spatial coherence score

空间相干性得分

Para_01

1. 我们使用联合计数统计量来量化域标签的空间一致性，这是一种在地理统计文献中发展起来的测量方法。
2. 从高层次来看，联合计数统计量计算了相邻斑点具有相同标签的对数与随机分配标签到斑点相比的 z 分数。
3. 较小的联合计数统计量表明邻近斑点的标签分布接近均匀分布，即标签在空间上是不一致的；而较大的联合计数统计量则表明邻近斑点经常具有相同的标签，即标签在空间上是一致的。 错误！！！ - 待补充

Para_03

1. 其中，μ_Jk = Pk^2 |E| 和 σ_Jk = √((1 - Pk)^2 Pk^2 |E|) 分别是 Jk 在零模型下的均值和标准差，在该零模型中，每个顶点标签为 k 的概率为 Pk。

Data collection and comparison methods

数据收集和比较方法

Para_01

1. 对于小脑分析，在章节‘GASTON再现了小鼠小脑的空间组织’和‘GASTON揭示了连续和不连续的变化’中，我们使用了RCTD/C-SIDE数据存储库的复制1。
2. 对于图3a中的标记基因比较，我们为每种方法得出一个基因排名，并评估了与已知的小脑少突胶质细胞、颗粒细胞、浦肯野细胞、贝格曼胶质细胞和分子细胞类型的标记基因相比的AUPRC。
3. 这些标记基因结合了来自PanglaoDB、Allen小鼠脑图谱、Harmonizome和参考文献补充资料中的细胞类型标记基因。

Para_02

1. 我们从参考文献中获得了嗅球 SRT 数据集。我们通过使用 scANVI 将 SRT 数据与独立的小鼠嗅球单细胞 RNA 测序数据集整合，获得了组织中每个点的细胞类型注释（图 6d）；对于单细胞 RNA 测序数据，我们遵循了参考文献中的预处理步骤。
2. 我们通过使用 scANVI 将 SRT 数据与独立的小鼠嗅球单细胞 RNA 测序数据集整合，获得了组织中每个点的细胞类型注释（图 6d）；
3. 对于单细胞 RNA 测序数据，我们遵循了参考文献中的预处理步骤。

Data availability

Para_01

1. 本文分析了现有的公开可用数据。
2. 小脑 SRT 数据集来自文献；
3. 嗅球 SRT 数据集来自文献；
4. CRC 肿瘤 SRT 数据集来自文献；
5. DLPFC SRT 数据集来自文献；
6. 乳腺癌 SRT 数据集来自 10X Genomics Xenium 门户，网址为 https://www.10xgenomics.com/products/xenium-in-situ/preview-dataset-human-breast；
7. 小鼠胚胎 SRT 数据集来自文献；
8. 小鼠大脑皮层数据集来自文献。

Code availability

Para_01

1. GASTON 的代码公开发布在 https://github.com/raphael-group/GASTON 和通过 Zenodo 在 https://doi.org/10.5281/zenodo.12702592。
2. 重现小脑、乳腺癌肿瘤、CRC 癌症肿瘤和小鼠皮层分析的教程公开发布在 https://gaston.readthedocs.io/en/latest/notebooks/tutorials/index.html。