Stata:DDML双重机器学习--ddml
ddml 估计分四个步骤进行
第 1 步:初始化 ddml 并选择模型
ddml init model [if] [in] [ , mname(name) kfolds(integer) fcluster(varname) foldvar(varlist) reps(integer) norandom
tabfold vars(varlist) ]
其中 ,模型 在部分线性模型(部分)、交互式模型(交互式)、部分线性 IV 模型 (IV)、灵活的部分线性 IV 模型 (FIV) 和交互式 IV 模型(交互式 IV)之间进行选择。
第 2 步:添加监督式机器学习以估计条件期望。
在第 2 步中,我们选择用于估计 CEF 的机器学习程序。
ddml eq [ , mname(name) vname(varname) learner(varname) vtype(string) predopt(string) ] : command depvar vars [ , cmdopt ]
第 3 步:执行交叉拟合
ddml crossfit [ , mname(name) shortstack ]
此步骤实现交叉拟合算法。每个学习在训练折叠上迭代拟合,并获得样本外预测值。
交叉拟合是最耗时的步骤,因为它涉及重复拟合选定的机器学习方法。
第 4 步:估计因果效应。
ddml estimate [ , mname(name) robust cluster(varname) vce(type) atet ateu trim(real) ]
Stata应用案例1
我们使用两个应用案例演示 ddml 工作。
应用 DDML 估计来估计 401(k) 资格对金融财富的影响,遵循 Poterba、Venti 和 Wise (1995)。
为简洁起见,我们重点介绍部分线性模型,但提供了代码,演示了如何将 ddml 与交互式模型、部分线性 IV 模型和交互式 IV 模型一起使用,使用在线附录 C 中的相同应用程序。
基于 Berry、Levinsohn 和 Pakes (1995),可以使用 ddml 来估计灵活的部分线性 IV 模型,该模型既可以使用混杂因素的高维函数近似灵活地控制混杂因素,也可以估计最佳 IV。
该数据包括 n = 9915 个来自 1991 年收入和计划参与调查的家庭。
该应用最初是由于 Poterba、Venti 和 Wise (1995) 的,但 Belloni 等人(2017 年)、Chernozhukov 等人(2018 年)以及 Wüthrich 和 Zhu (2023 年)等人重新审视了该应用。
根据以前的研究,我们包括控制变量年龄、收入、受教育年限和家庭规模,以及婚姻状况、双收入者状况、福利养老金状况、个人退休账户参与和房屋所有权等指标。结果是净金融资产,而处理变量是有资格参加 401(k) 养老金计划。
我们加载数据并为结果、处理变量和控制变量定义三个全局变量。
然后,我们执行DDMl分析需要的四个步骤。
use sipp1991
global Y net_tfa
global X age inc educ fsize marr twoearn db pira hown
global D e401
步骤 1:初始化 ddml 模型
我们初始化 ddml 模型并选择部分线性模型。
在初始化之前,我们设置种子以确保复制。
这应始终在 ddml init 之前完成,该 init 执行随机折叠分配。
在此示例中,我们选择 4 折来确保下面显示的某些输出的可读性,但我们建议在实践中考虑更多折。
第 2 步:添加监督式机器学习来估计条件期望
在此步骤中,我们指定应该使用哪些机器学习程序来估计条件期望 E(Y |X) 和 E(
D|X) 。
对于每个有条件的期望,至少需要一个机器学习。
为了说明目的,我们考虑使用回归进行线性回归,使用 pystacked 对应的m(lassocv) 选项进行 进行交叉验证的Lasso回归(作为如何使用 pystacked 估计一个学习的示例),以及用于随机森林的rforest。
在使用 rforest 时,我们需要添加选项 vtype(none),因为 rforest 的 postestimation predict 命令不支持变量类型。
灵活的 ddml 语法允许为不同的机器学习指定不同的协变量集。
这种灵活性可能很有用,因为例如,如果将交互作为输入提供,线性学习器(如套索)可能会表现得更好,而基于树的方法(如随机森林)可能会以数据驱动的方式检测某些交互。在这里,我们对交叉验证的套索使用交互和二阶多项式,但不对其他学习者使用交互和二阶多项式。
此应用程序只有一个 treatment 变量,但 ddml 确实支持多个 treatment 变量。要添加第二个处理变量,我们只需添加一个语句,例如 ddml E[D|X]:reg D2 $X,其中 D2 将是第二个处理变量的名称。帮助文件中提供了包含两种处理的示例。
ddml 子命令 describe 允许我们验证学习是否已正确注册:
第 3 步:执行交叉拟合
第 3 步执行交叉拟合,这是最耗时的过程。shortstack 选项启用了short-stacking 算法。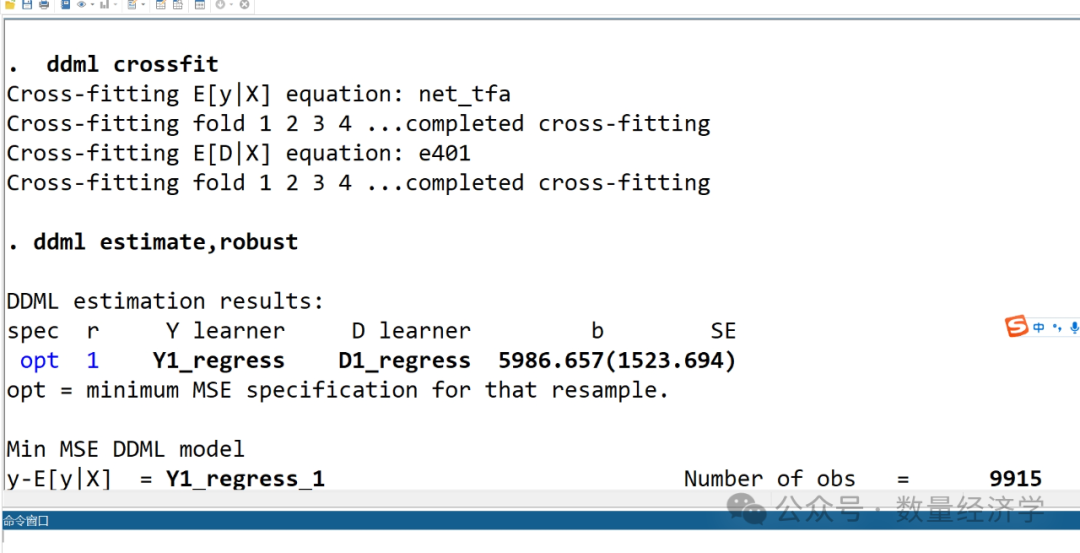
第 4 步:估计因果效应。
在最后一步中,我们获得因果效应估计值。由于我们在步骤 3 中请求了 shortstacking,因此 ddml 显示了 short-stacking 结果,该结果依赖于每个基本学习的交叉拟合值。
此外,输出的开头还列出了与最小 MSE 学习者相对应的规范。