机器学习基础——从头开始带大家实现线性回归！

什么是线性回归？
线性回归是一种简单的方法，它试图在众多点中绘制出一条直线。这条直线能帮助我们根据某种模式进行预测。

例如，如果你知道一个学生的学习时长，你可能想预测他们的成绩，学习时间越长成绩往往越好，线性回归就能找出这种模式。

这条直线的形式如下：

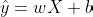
其中：

X 是输入（比如学习时长）
y 是输出（比如成绩）
w 是斜率（表示直线的倾斜程度）
b 是截距（直线与 y 轴的交点）

线性回归应用于哪些场景？

预测房价
销售预测
预测学生成绩
分析健康趋势
股票市场预测

手动数学示例——线性回归逐步解析
下面我们手动通过一个简单示例，仅使用两个变量和三个数据点来进行说明。

给定数据点

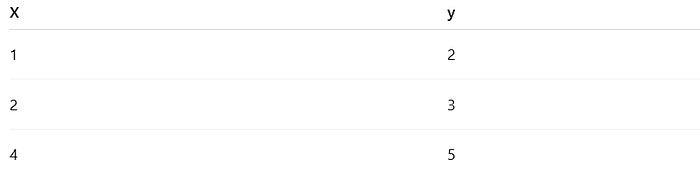
我们想要拟合一条直线：

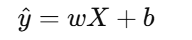
步骤 1：计算均值

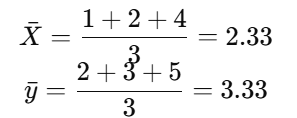
步骤 2：计算斜率（w）

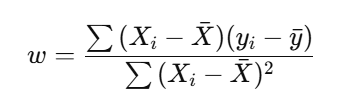
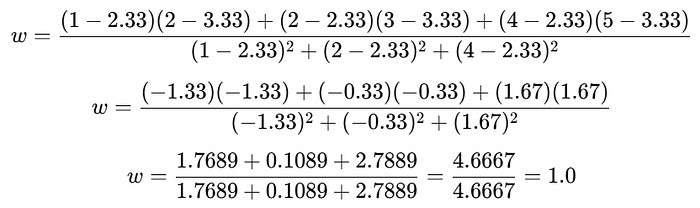
步骤 3：计算截距（b）

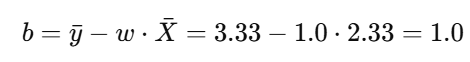
最终方程

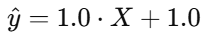
这就是回归直线，现在我们可以用它来预测任意学习时长对应的成绩。

步骤 4：预测

Python 代码（从零开始）

下面展示如何在不使用任何机器学习库的情况下，在 Python 中逐步实现相同的功能。

# Our data
X = [1, 2, 4]
y = [2, 3, 5]

# Step 1: Find the means
mean_x = sum(X) / len(X)
mean_y = sum(y) / len(y)

# Step 2: Calculate slope (w)
numerator = 0
denominator = 0
for i inrange(len(X)):
    numerator += (X[i] - mean_x) * (y[i] - mean_y)
    denominator += (X[i] - mean_x) ** 2

w = numerator / denominator

# Step 3: Calculate intercept (b)
b = mean_y - w * mean_x

# Final model
print("The equation of the line is: y = {:.2f}x + {:.2f}".format(w, b))

# Step 4: Make predictions
print("\nPredictions:")
for i inrange(len(X)):
    y_pred = w * X[i] + b
print


    
(f"When X = {X[i]}, y_actual = {y[i]}, y_predicted = {y_pred:.2f}")

The equation of the line is: y = 1.00x + 1.00

Predictions:
When X = 1, y_actual = 2, y_predicted = 2.00
When X = 2, y_actual = 3, y_predicted = 3.00
When X = 4, y_actual = 5, y_predicted = 5.00

在此情况下，预测值与实际值完全匹配，这表明对于这三个点，我们的直线与数据完美拟合。

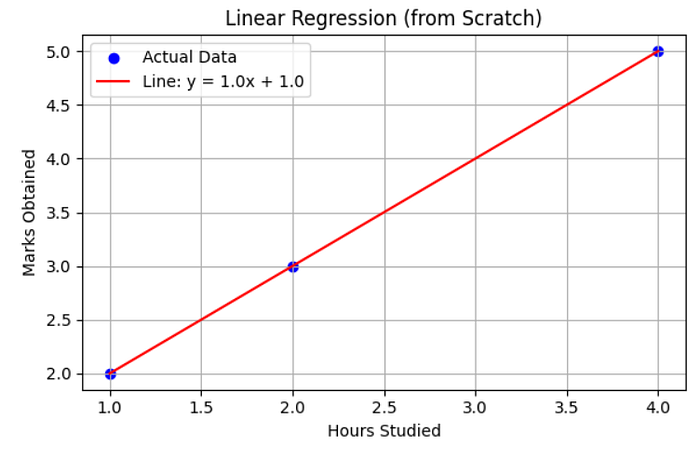
图表还展示了：

蓝色圆点：实际数据点（学习时长与成绩）
红色直线：基于我们公式的预测直线

这条直线展示了随着学习时间的增加，成绩是如何提

高的。

所以，如果有人学习 3 个小时，我们可以使用方程：

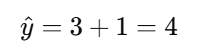
来预测他们将获得 4 分。

另外我们精心打磨了一套基于数据与模型方法的AI科研入门学习方案（已经迭代第6次），对于人工智能来说，任何专业，要处理的都只是实验数据，所以我们根据实验数据将课程分为了三种方向的针对性课程，包含时序、影像、AI＋实验室，我们会根据你的数据类型来帮助你选择合适的实验室，根据规划好的路线学习 只需3-5个月左右（很多同学通过学习已经发表了 sci 一区及以下、和同等级别的会议论文）学习形式为直播＋录播，多位老师为你的论文保驾护航。