小心！你的DDL变更可能正悄悄搞垮MySQL性能……

业务同学在 OneDBA 平台进行一次正常 DDL 变更完成后（变更内容跟此次问题无关），发现一些 SQL 开始出现慢查，同时变更后的表比变更前的表存储空间膨胀了几乎 100%。经过分析和流程复现完整还原了整个事件，发现了 MySQL 在平衡 B+tree 页分裂方面遇到单行记录太大时的一些缺陷，整理分享。

为了能更好的说明问题背后的机制，会进行一些关键的“MySQL原理”和“当前DDL变更流程”方面的知识铺垫，熟悉的同学可以跳过。

本次 DDL 变更后带来了如下问题：

• 变更后，表存储空间膨胀了几乎 100%；

• 变更后，表统计信息出现了严重偏差；

• 变更后，部分有排序的 SQL 出现了慢查。

现在来看，表空间膨胀跟统计信息出错是同一个问题导致，而统计信息出错间接导致了部分SQL出现了慢查，下面带着这些问题开始一步步分析找根因。

InnoDB 表是索引组织表，也就是所谓的索引即数据，数据即索引。索引分为聚集索引和二级索引，所有行数据都存储在聚集索引，二级索引存储的是字段值和主键，但不管哪种索引，其结构都是 B+tree 结构。

一棵 B+tree 分为根页、非叶子节点和叶子节点，一个简单的示意图（from Jeremy Cole）如下：

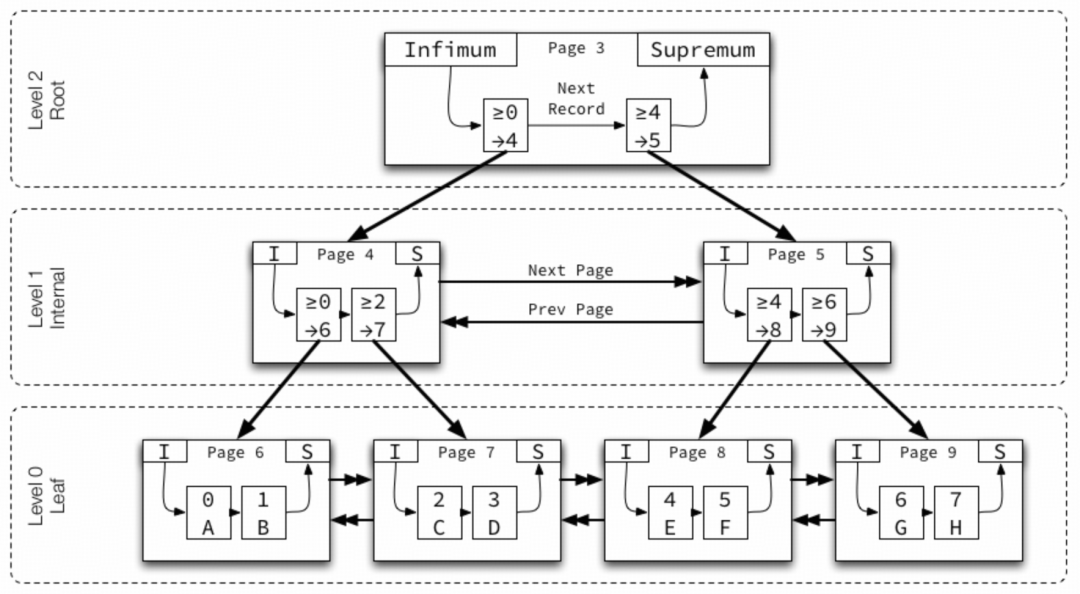
由于 InnoDB B+tree 结构高扇区特性，所以每个索引高度基本在 3-5 层之间，层级（Level）从叶子节点的 0 开始编号，沿树向上递增。每层的页面节点之间使用双向链表，前一个指针和后一个指针按key升序排列。

最小存储单位是页，每个页有一个编号，页内的记录使用单向链表，按 key 升序排列。每个数据页中有两个虚拟的行记录，用来限定记录的边界；其中最小值（Infimum）表示小于页面上任何 key 的值，并且始终是单向链表记录列表中的第一个记录；最大值（Supremum）表示大于页面上任何 key 的值，并且始终是单向链表记录列表中的最后一条记录。这两个值在页创建时被建立，并且在任何情况下不会被删除。

非叶子节点页包含子页的最小 key 和子页号，称为“节点指针”。

现在我们知道了我们插入的数据最终根据主键顺序存储在叶子节点（页）里面，可以满足点查和范围查询的需求。

默认一个页 16K 大小，且 InnoDB 规定一个页最少能够存储两行数据，这里需要注意规定一个页最少能够存储两行数据是指在空间分配上，并不是说一个页必须要存两行，也可以存一行。

怎么实现一个页必须要能够存储两行记录呢？ 当一条记录 <8k 时会存储在当前页内，反之 >8k 时必须溢出存储，当前页只存储溢出页面的地址，需 20 个字节（行格式：Dynamic），这样就能保证一个页肯定能最少存储的下两条记录。

当一个记录 >8k 时会循环查找可以溢出存储的字段，text类字段会优先溢出，没有就开始挑选 varchar 类字段，总之这是 InnoDB 内部行为，目前无法干预。

建表时无论是使用 text 类型，还是 varchar 类型，当大小 <8k 时都是存储在当前页，也就是在 B+tree 结构中，只有 >8k 时才会进行溢出存储。

随着表数据的变化，对记录的新增、更新、删除；那么如何在 B+tree 中高效管理动态数据也是一项核心挑战。

MySQL InnoDB 引擎通过页面分裂和页面合并两大关键机制来动态调整存储结构，不仅能确保数据的逻辑完整性和逻辑顺序正确，还能保证数据库的整体性能。这些机制发生于 InnoDB 的 B+tree 索引结构内部，其具体操作是：

• 页面分裂：当已满的索引页无法容纳新记录时，创建新页并重新分配记录。

• 页面合并：当页内记录因删除/更新低于阈值时，与相邻页合并以优化空间。

深入理解上述机制至关重要，因为页面的分裂与合并将直接影响存储效率、I/O模式、加锁行为及整体性能。其中页面的分裂一般分为两种：

• 中间点（mid point）分裂：将原始页面中50%数据移动到新申请页面，这是最普通的分裂方法。

  
  

• 插入点（insert point）分裂：判断本次插入是否递增 or 递减，如果判定为顺序插入，就在当前插入点进行分裂，这里情况细分较多，大部分情况是直接插入到新申请页面，也可能会涉及到已存在记录移动到新页面，有有些特殊情况下还会直接插入老的页面（老页面的记录被移动到新页面）。

在整个数据库平台（OneDBA）构建过程中，MySQL 结构变更模块是核心基础能力，也是研发同学在日常业务迭代过程中使用频率较高的功能之一，主要围绕对表加字段、加索引、改属性等操作，为了减少这些操作对线上数据库或业务的影响，早期便为 MySQL 结构变更开发了一套基于容器运行的无锁变更程序，核心采用的是全量数据复制+增量 binlog 回放来进行变更，也是业界通用做法（内部代号：dw-osc，基于 GitHub 开源的 ghost 工具二次开发），主要解决的核心问题：

• 实现无锁化的结构变更，变更过程中不会阻挡业务对表的读写操作。

• 实现变更不会导致较大主从数据延迟，避免业务从库读取不到数据导致业务故障。

• 实现同时支持大规模任务变更，使用容器实现使用完即销毁，无变更任务时不占用资源。

变更工具工作原理简单描述（重要）：

这里顺便说一下当前得物结构变更整体架构：由于变更工具的工作原理需消费大量 binlog 日志保证数据一致性，会导致在变更过程中会有大量的带宽占用问题，为了消除带宽占用问题，开发了 Proxy 代理程序，在此基础之上支持了多云商、多区域本地化变更。

目前整体架构图如下：

上面几个关键点铺垫完了，回到第一个问题，这里先直接说明根本原因，后面会阐述一下排查过程（有同学感兴趣所以分享一下，整个过程还是耗费不少时间）。

在『结构变更机制』介绍中，我们发现这种变更机制它有一个特点，就是【第三步】会导致新插入的记录可能会先写入到表中（主键 ID 大的记录先写入到了表），然后【第二步】中复制数据后写入到表中（主键 ID 小的记录）。这种写入特性叠加单行记录过大的时候（业务表单行记录大小 5k 左右），会碰到 MySQL 页分裂的一个瑕疵（暂且称之为瑕疵，或许是一个 Bug），导致了一个页只存储了 1 条记录（16k 的页只存储了 5k，浪费 2/3 空间），放大了存储问题。

下面直接复现一下这种现象下导致异常页分裂的过程：

CREATE TABLE `sbtest` (  `id` int(11) NOT NULL AUTO_INCREMENT,  `pad` varchar(12000),  PRIMARY KEY (`id`)) ENGINE=InnoDB;

然后插入两行 5k 大小的大主键记录（模拟变更时 binlog 回放先插入数据）：

insert into sbtest values (10000, repeat('a',5120));insert into sbtest values (10001, repeat('a',5120));

这里写了一个小工具打印记录对应的 page 号和 heap 号。

# ./peng[pk:10000] page: 3 -> heap: 2[pk:10001] page: 3 -> heap: 3

可以看到两条记录都存在 3 号页，此时表只有这一个页。

继续开始顺序插入数据（模拟变更时 copy 全量数据过程），插入 rec-1：

insert into sbtest values (1, repeat('a',5120));

# ./peng[pk:1] page: 3 -> heap: 4[pk:10000] page: 3 -> heap: 2[pk:10001] page: 3 -> heap: 3

插入 rec-2：

insert into sbtest values (2, repeat('a',5120));

# ./peng[pk:1] page: 4 -> heap: 2[pk:2] page: 4 -> heap: 3[pk:10000] page: 5 -> heap: 2[pk:10001] page: 5 -> heap: 3

可以看到开始分裂了，page 3 被提升为根节点了，同时分裂出两个叶子节点，各自存了两条数据。此时已经形成了一棵 2 层高的树，还是用图表示吧，比较直观，如下：

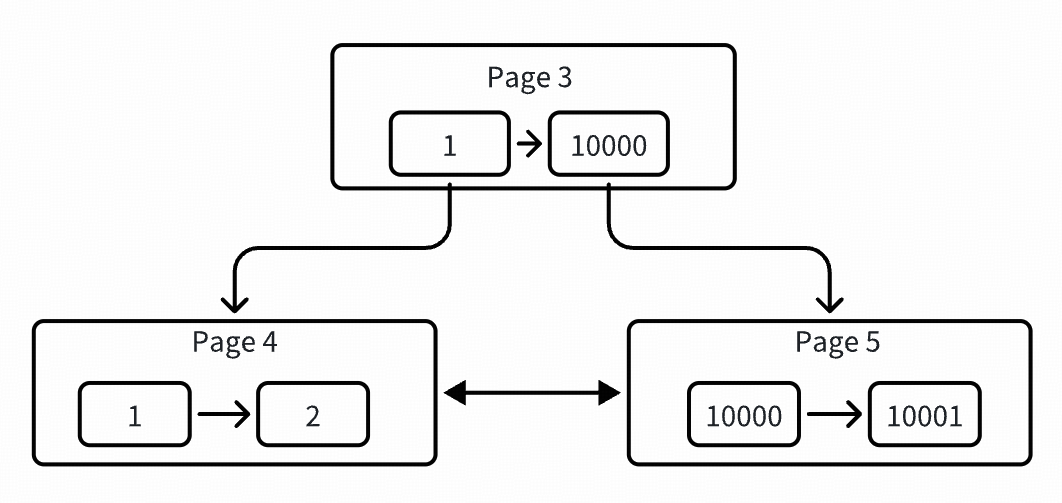
插入 rec-3：

insert into sbtest values (3, repeat('a',5120));

# ./peng[pk:1] page: 4 -> heap: 2[pk:2] page: 4 -> heap: 3[pk:3] page: 5 -> heap: 4[pk:10000] page: 5 -> heap: 2[pk:10001] page: 5 -> heap: 3

示意图如下：

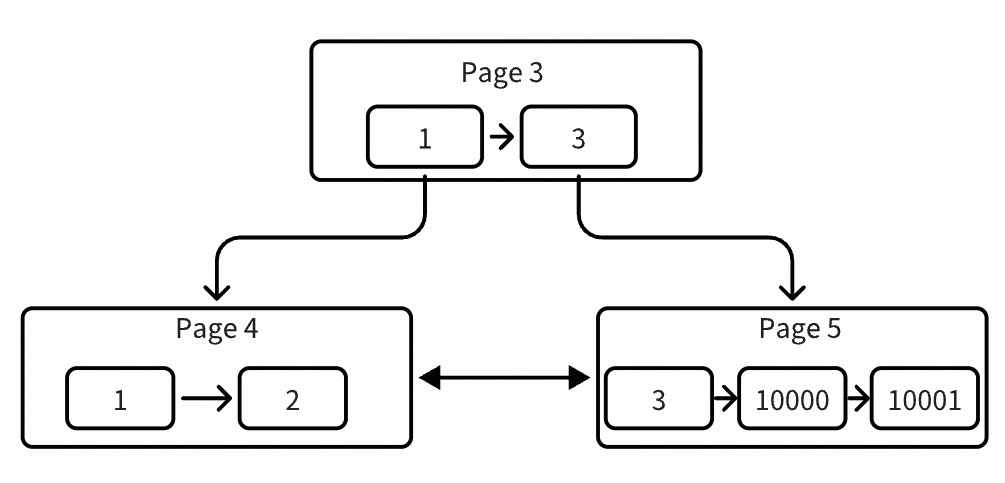
插入 rec-4：

insert into sbtest values (4, repeat('a',5120));

# ./peng[pk:1] page: 4 -> heap: 2[pk:2] page: 4 -> heap: 3[pk:3] page: 5 -> heap: 4[pk:4] page: 5 -> heap: 3[pk:10000] page: 5 -> heap: 2[pk:10001] page: 6 -> heap: 2

这里开始分裂一个新页 page 6，开始出现比较复杂的情况，同时也为后面分裂导致一个页只有 1 条数据埋下伏笔：

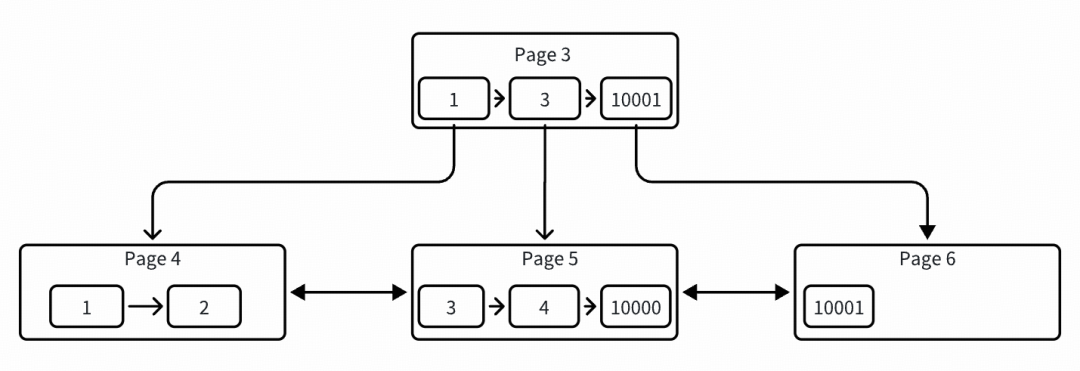
这里可以看到把 10001 这条记录从 page 5 上面迁移到了新建的 page 6 上面（老的 page 5 中会删除 10001 这条记录，并放入到删除链表中），而把当前插入的 rec-4 插入到了原来的 page 5 上面，这个处理逻辑在代码中是一个特殊处理，向右分裂时，当插入点页面前面有大于等于两条记录时，会设置分裂记录为 10001，所以把它迁移到了 page 6，同时会把当前插入记录插入到原 page 5。具体可以看 btr_page_get_split_rec_to_right 函数。

/* 这里返回true表示将行记录向右分裂：即分配的新page的hint_page_no为原page+1 */ibool btr_page_get_split_rec_to_right(/*============================*/        btr_cur_t*        cursor,        rec_t**           split_rec){  page_t*        page;  rec_t*        insert_point;
  // 获取当前游标页和insert_point  page = btr_cur_get_page(cursor);  insert_point = btr_cur_get_rec(cursor);
  /* 使用启发式方法：如果新的插入操作紧跟在同一页面上的前一个插入操作之后，     我们假设这里存在一个顺序插入的模式。 */
  // PAGE_LAST_INSERT代表上次插入位置，insert_point代表小于等于待插入目标记录的最大记录位置  // 如果PAGE_LAST_INSERT=insert_point意味着本次待插入的记录是紧接着上次已插入的记录，  // 这是一种顺序插入模式，一旦判定是顺序插入，必然反回true，向右分裂  if (page_header_get_ptr(page, PAGE_LAST_INSERT) == insert_point) {    // 1. 获取当前insert_point的page内的下一条记录，并判断是否是supremum记录    // 2. 如果不是，继续判断当前insert_point的下下条记录是否是supremum记录    // 也就是说，会向后看两条记录，这两条记录有一条为supremum记录，    // split_rec都会被设置为NULL，向右分裂    rec_t*        next_rec;    next_rec = page_rec_get_next(insert_point);        if (page_rec_is_supremum(next_rec)) {    split_at_new:      /* split_rec为NULL表示从新插入的记录开始分裂，插入到新页 */      *split_rec = nullptr;    } else {      rec_t* next_next_rec = page_rec_get_next(next_rec);      if (page_rec_is_supremum(next_next_rec)) {        goto split_at_new;      }            /* 如果不是supremum记录，则设置拆分记录为下下条记录 */
      /* 这样做的目的是，如果从插入点开始向上有 >= 2 条用户记录，         我们在该页上保留 1 条记录，因为这样后面的顺序插入就可以使用         自适应哈希索引，因为它们只需查看此页面上的记录即可对正确的         搜索位置进行必要的检查 */            *split_rec = next_next_rec;    }        return true;  }
  return false;}

插入 rec-5：

insert into sbtest values (5, repeat('a',5120));

# ./peng[pk:1] page: 4 -> heap: 2[pk:2] page: 4 -> heap: 3[pk:3] page: 5 -> heap: 4[pk:4] page: 5 -> heap: 3[pk:5] page: 7 -> heap: 3[pk:10000] page: 7 -> heap: 2[pk:10001] page: 6 -> heap: 2

开始分裂一个新页 page 7，新的组织结构方式如下图：

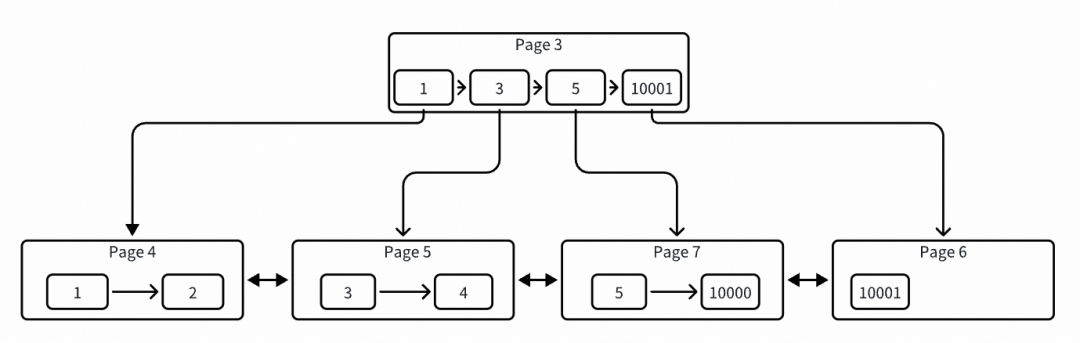
此时是一个正常的插入点右分裂机制，把老的 page 5 中的记录 10000 都移动到了 page 7，并且新插入的 rec-5 也写入到了 page 7 中。到此时看上去一切正常，接下来再插入记录在当前这种结构下就会产生异常。

插入 rec-6：

insert into sbtest values (5, repeat('a',5120));

# ./peng[pk:1] page: 4 -> heap: 2[pk:2] page: 4 -> heap: 3[pk:3] page: 5 -> heap: 4[pk:4] page: 5 -> heap: 3[pk:5] page: 7 -> heap: 3[pk:6] page: 8 -> heap: 3[pk:10000] page: 8 -> heap: 2[pk:10001] page: 6 -> heap: 2

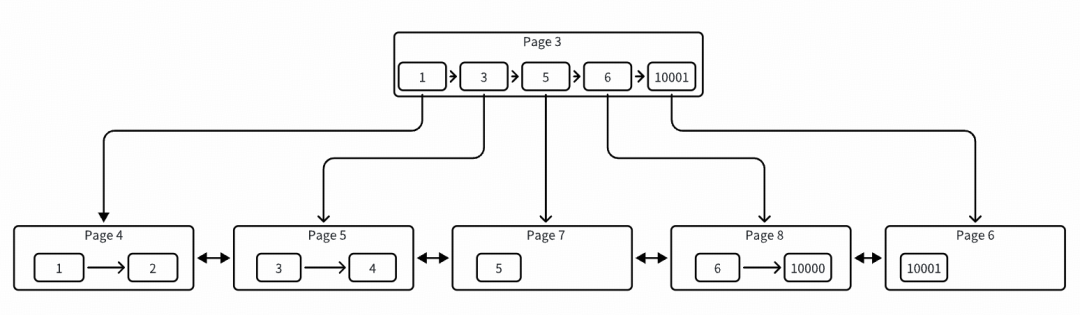
此时也是一个正常的插入点右分裂机制，把老的 page 7 中的记录 10000 都移动到了 page 8，并且新插入的 rec-6 也写入到了 page 8 中，但是我们可以发现 page 7 中只有一条孤零零的 rec-5 了，一个页只存储了一条记录。

按照代码中正常的插入点右分裂机制，继续插入 rec-7 会导致 rec-6 成为一个单页、插入 rec-8 又会导致 rec-7 成为一个单页，一直这样循环下去。

目前来看就是在插入 rec-4，触发了一个内部优化策略（具体优化没太去研究），进行了一些特殊的记录迁移和插入动作，当然跟记录过大也有很大关系。

有同学对这个问题排查过程比较感兴趣，所以这里也整理分享一下，简化了一些无用信息，仅供参考。

表总行数在 400 百万，正常情况下的大小在 33G 左右，变更之后的大小在 67G 左右。

• 首先根据备份恢复了一个数据库现场出来。

  
  

• 统计了业务表行大小，发现行基本偏大，在 4-7k 之间（一个页只存了2行，浪费1/3空间）。

• 分析了变更前后的表数据页，以及每个页存储多少行数据。

• 发现变更之前数据页大概 200 百万，变更之后 400 百万，解释了存储翻倍。

• 发现变更之前存储 1 行的页基本没有，变更之后存储 1 行的页接近 400 百万。

基于现在这些信息我们知道了存储翻倍的根本原因，就是之前一个页存储 2 条记录，现在一个页只存储了 1 条记录，新的问题来了，为什么变更后会存储 1 条记录，继续寻找答案。

• 我们首先在备份恢复的实例上面进行了一次静态变更，就是变更期间没有新的 DML 操作，没有复现。但说明了一个问题，异常跟增量有关，此时大概知道跟变更过程中的 binlog 回放特性有关【上面说的回放会导致主键 ID 大的记录先写入表中】。

  
  

• 写了个工具把 400 百万数据每条记录分布在哪个页里面，以及页里面的记录对应的 heap 是什么都记录到数据库表中分析，慢长等待跑数据。

• 数据分析完后通过分析发现存储一条数据的页对应的记录的 heap 值基本都是 3，正常应该是 2，意味着这些页并不是一开始就存一条数据，而是产生了页分裂导致的。

  
  

• 开始继续再看页分裂相关的资料和代码，列出页分裂的各种情况，结合上面的信息构建了一个复现环境。插入数据页分裂核心函数。

• btr_cur_optimistic_insert：乐观插入数据，当前页直接存储

• btr_cur_pessimistic_insert：悲观插入数据，开始分裂页

• btr_root_raise_and_insert：单独处理根节点的分裂

• btr_page_split_and_insert：分裂普通页，所有流程都在这个函数

• btr_page_get_split_rec_to_right：判断是否是向右分裂

• btr_page_get_split_rec_to_left：判断是否是向左分裂

表统计信息主要涉及索引基数统计（也就是唯一值的数量），主键索引的基数统计也就是表行数，在优化器进行成本估算时有些 SQL 条件会使用索引基数进行抉择索引选择（大部分情况是 index dive 方式估算扫描行数）。

InnoDB 统计信息收集算法简单理解就是采样叶子节点 N 个页（默认 20 个页），扫描统计每个页的唯一值数量，N 个页的唯一值数量累加，然后除以N得到单个页平均唯一值数量，再乘以表的总页面数量就估算出了索引总的唯一值数量。

但是当一个页只有 1 条数据的时候统计信息会产生严重偏差（上面已经分析出了表膨胀的原因就是一个页只存储了 1 条记录），主要是代码里面有个优化逻辑，对单个页的唯一值进行了减 1 操作，具体描述如下注释。本来一个页面就只有 1 条记录，再进行减 1 操作就变成 0 了，根据上面的公式得到的索引总唯一值就偏差非常大了。

static bool dict_stats_analyze_index_for_n_prefix(    ...    // 记录页唯一key数量    uint64_t n_diff_on_leaf_page;        // 开始进行dive，获取n_diff_on_leaf_page的值    dict_stats_analyze_index_below_cur(pcur.get_btr_cur(), n_prefix,                                       &n_diff_on_leaf_page, &n_external_pages);        /* 为了避免相邻两次dive统计到连续的相同的两个数据，因此减1进行修正。    一次是某个页面的最后一个值，一次是另一个页面的第一个值。请考虑以下示例：    Leaf level:    page: (2,2,2,2,3,3)    ... 许多页面类似于 (3,3,3,3,3,3)...    page: (3,3,3,3,5,5)    ... 许多页面类似于 (5,5,5,5,5,5)...    page: (5,5,5,5,8,8)    page: (8,8,8,8,9,9)    我们的算法会（正确地）估计平均每页有 2 条不同的记录。    由于有 4 页 non-boring 记录，它会（错误地）将不同记录的数量估计为 8 条    */     if (n_diff_on_leaf_page > 0) {      n_diff_on_leaf_page--;    }        // 更新数据，在所有分析的页面上发现的不同键值数量的累计总和    n_diff_data->n_diff_all_analyzed_pages += n_diff_on_leaf_page;)

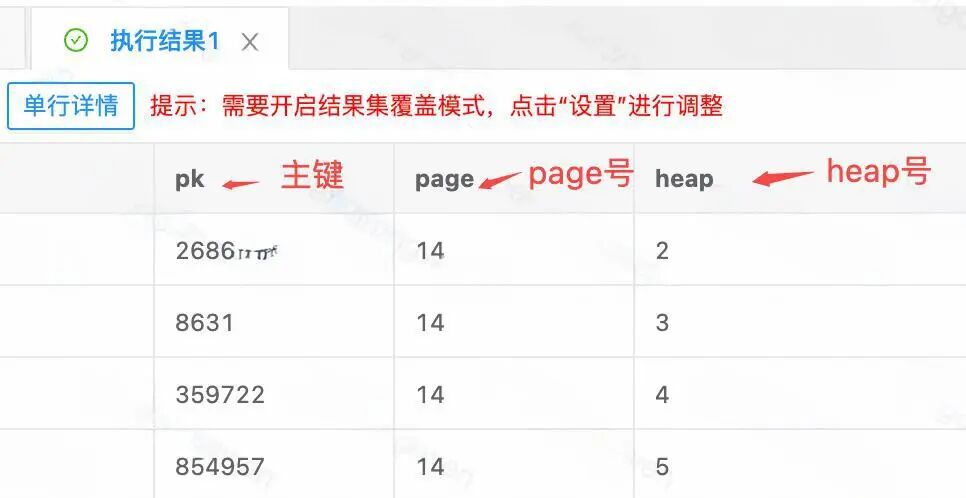
可以看到PRIMARY主键异常情况下统计数据只有 20 万，表有 400 百万数据。正常情况下主键统计数据有 200 百万，也与表实际行数差异较大，同样是因为单个页面行数太少（正常情况大部分也只有2条数据），再进行减1操作后，导致统计也不准确。

MySQL> select table_name,index_name,stat_value,sample_size from mysql.innodb_index_stats where database_name like 'sbtest' and TABLE_NAME like 'table_1' and stat_name='n_diff_pfx01';+-------------------+--------------------------------------------+------------+-------------+| table_name        | index_name                                 | stat_value | sample_size |+-------------------+--------------------------------------------+------------+-------------+| table_1           | PRIMARY                                    |     206508 |          20 |+-------------------+--------------------------------------------+------------+-------------+11 rows in set (0.00 sec)

当前 MySQL 对大部分 SQL 在评估扫描行数时都不再依赖统计信息数据，而是通过一种 index dive 采样算法实时获取大概需要扫描的数据，这种方式的缺点就是成本略高，所以也提供有参数来控制某些 SQL 是走 index dive 还是直接使用统计数据。

另外在SQL带有 order by field limit 时会触发MySQL内部的一个关于 prefer_ordering_index 的 ORDER BY 优化，在该优化中，会比较使用有序索引和无序索引的代价，谁低用谁。

当时业务有问题的慢 SQL 就是被这个优化干扰了。

# where条件user_id = ? and biz = ? and is_del = ? and status in (?) ORDER BY modify_time limit 5# 表索引idx_modify_time(`modify_time`)idx_user_biz_del(`user_id`,`biz`, `is_del`)

正常走 idx_user_biz_del 索引为过滤性最好，但需要对 modify_time 字段进行排序。

这个优化机制就是想尝试走 idx_modify_time 索引，走有序索引想避免排序，然后套了一个公式来预估如果走 idx_modify_time 有序索引大概需要扫描多少行？公式非常简单直接：表总行数 / 最优索引的扫描行数 * limit。

• 表总行数：也就是统计信息里面主键的 n_rows

• 最优索引的扫描行数：也就是走 idx_user_biz_del 索引需要扫描的行数

• limit：也就是 SQL 语句里面的 limit 值

使用有序索引预估的行数对比最优索引的扫描行数来决定使用谁，在这种改变索引的策略下，如果表的总行数估计较低（就是上面主键的统计值），会导致更倾向于选择有序索引。

但一个最重要的因素被 MySQL 忽略了，就是实际业务数据分布并不是按它给的这种公式来，往往需要扫描很多数据才能满足 limit 值，造成慢 SQL。

发现问题后，可控的情况下选择在低峰期对表执行原生 alter table xxx engine=innodb 语句， MySQL 内部重新整理了表空间数据，相关问题恢复正常。但这个原生 DDL 语句，虽然变更不会产生锁表，但该语句无法限速，同时也会导致主从数据较大延迟。

为什么原生 DDL 语句可以解决该问题？看两者在流程上的对比区别。

可以看出结构变更唯一不同的就是增量 DML 语句是等全量数据复制完成后才开始应用，所以能修复表空间，没有导致表膨胀。

关于业务侧的改造这里不做过多说明，我们看看从变更流程上面是否可以避免这个问题。

既然在变更过程中复制全量数据和 binlog 增量数据回放存在交叉并行执行的可能，那么如果我们先执行全量数据复制，然后再进行增量 binlog 回放是不是就可以绕过这个页分裂问题（就变成了跟 MySQL 原生 DDL 一样的流程）。

变更工具实际改动如下图：

这样就不存在最大记录先插入到表中的问题，丢弃的记录后续全量复制也同样会把记录复制到临时表中。并且这个优化还能解决需要大量回放 binlog 问题，细节可以看看 gh-ost 的 PR-1378。

本文先介绍了一些关于 InnoDB 索引机制和页溢出、页分裂方面的知识；介绍了业界通用的 DDL 变更工具流程原理。

随后详细分析了变更后表空间膨胀问题根因，主要是当前变更流程机制叠加单行记录过大的时候（业务表单行记录大小 5k 左右），会碰到 MySQL 页分裂的一个瑕疵，导致了一个页只存储了 1 条记录（16k 的页只存储了 5k，浪费 2/3 空间），导致存储空间膨胀问题。

最后分析了统计信息出错的原因和统计信息出错与慢 SQL 之间的关联关系，以及解决方案。