大家好，基于Python的数据科学实践课程又到来了，大家尽情学习吧。本期内容主要由程茜与政委联合推出。
在上一节中的模型参数估计中也会涉及到假设检验，但是这都是模型拟合过程中自动给出的结果。本章专门以方差分析为例展示Statsmodels模块的另一项主要功能。首先，大家思考这么一个问题。人们在选火锅团购产品时都习惯于在APP页面看每家店铺的评分，毕竟过来人的经验还是需要参靠地。细心的吃货就会问个问题：不同的评分团购产品的销量是否有差异？这就涉及到统计中的假设检验问题。用什么方法可以解决这个问题？方差分析。
方差分析是利用样本数据检验两个或两个以上总体均值间是否有差异的一种方法。根据研究变量的个数不用，分为单因素方差分析和多因素方差分析。如果我们要解决多个总体的均值是否有差异的检验问题，这就是单因素方差分析；如果是多个自变量对因变量影响，就是多因素方差分析。
一元单因素方差分析是研究单独一个因素对因变量的影响。首先根据这个单独的因素的不同水平对因变量进行分组，计算其组间和组内方差。之后，对各组的均值比较，最终对每个分组均值相等这个原假设进行检验。
以火锅团购数据为例，因变量是销量（购买人数）。每销售一单，客户都会对其进行评分。此时，我们可以来查看下数据集中的评分，如例1。
例1 火锅数据集
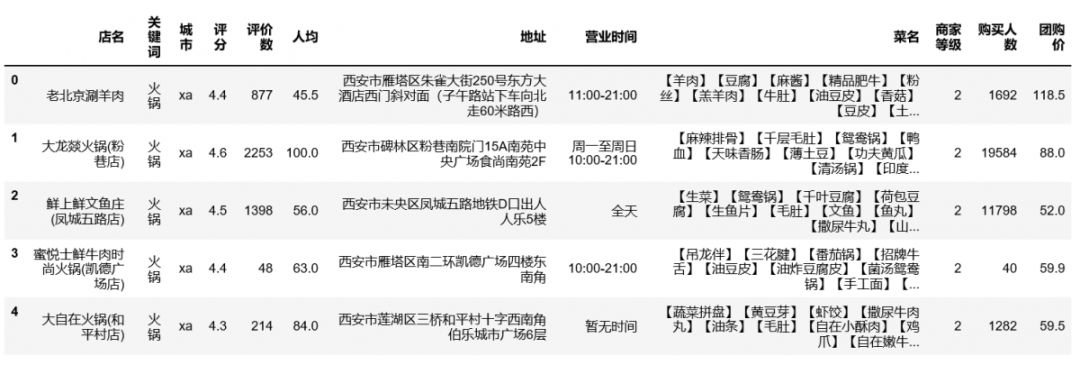
图1 数据前6行
对因变量购买人数做对数运算，并将“评分”变量转化为分类变量并给出其新的标签：
例2 数据离散化
#对购买人数做对数运算
for i in range(0,197):
data_shop.iloc[i,10]=math.log(data_shop.iloc[i,10])
#将评分离散化
评分_g=[0,4,4.5,5]
data_shop["评分_g"]=pd.cut(data_shop.评分,评分_g,labels=["小于4分","4-4.5分","4.5-5分"])此时，就完成了对评分的离散化，如图5.4-1-2
图2 离散后的数据集
对数据变换完以后，我们可以尝试着绘制箱线图来初步考察各评分水平对因变量的影响：
例3 绘制箱线图
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']
import seaborn as sns
sns.boxplot(x='评分_g',y='购买人数',data=data_shop)
plt.show()
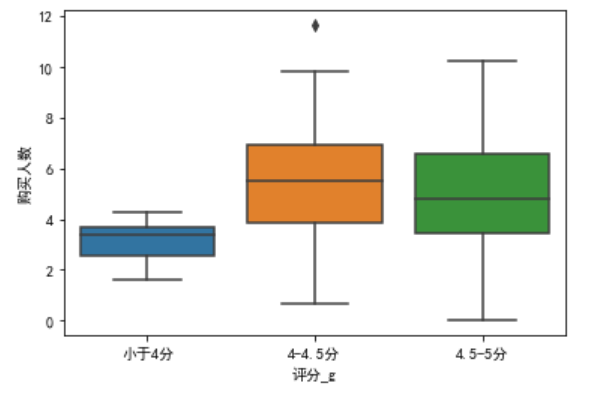
图3 各评分水平对购买人数的箱图
从图3中可明显看出，各种评分区间在“对数购买人数”上确实有显著区别。有的童鞋不禁要问了，是仅限于本案例的数据吗？那么，在整个火锅市场上购买人数是否会由于团购的评分不同而引起显著差异呢？那么这个问题就转化成了假设检验问题，需要进一步判定。
一元单因素方差分析主要研究单独一个自变量对因变量的影响。通过自变量的不同水平对因变量进行分组，计算其组间和组内方差，然后对各分组形成的总体进行均值比较，从而完成对各总体均值相等的原假设的检验。
本案例中，因变量是对数购买人数，人们吃完火锅后会对其进行打分，这中间加入了人为的影响因素，因此可以控制的定性变量就是评分，它会对对数购买人数产生影响。
Python的statsmodel模块中的anova_lm函数可以用来进行方差分析。如例4。
例4 方差分析
import statsmodels.api as sm
from statsmodels.formula.api import ols
data_shop_anova=sm.stats.anova_lm(ols("购买人数~C(评分_g)",data_shop).fit())
print(data_shop_anova)
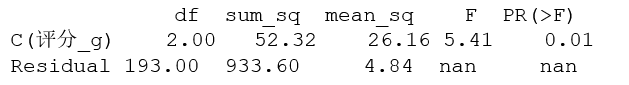
图4 方差分析结果
从结果可以看出，用于判定组内方差和组间方差是否存在差异的F值为5.41，其对应的P值=0.01，小于0.05。由此可知，在0.05的显著性水平下，拒绝各评分区间均值相等的原假设。也就是说，不同的评分区间，会对团购的对数购买人数产生非常显著的影响。所以很多商家会设计各种团购活动来提升各种质量来提高它的评分。这对于商家还是非常重要的，直接关乎销量。
当然，要想知道每类评分间的变动状况对对数购买人数产生的具体影响以及预测，就需要对此模型进行参数估计和预测。
可以通过构造模型对象来进行，如例5。
例5 参数估计
formula='购买人数~C(评分_g)'
data_shop_est=ols(formula,data_shop).fit()
print(data_shop_est.summary())
其结果如下：
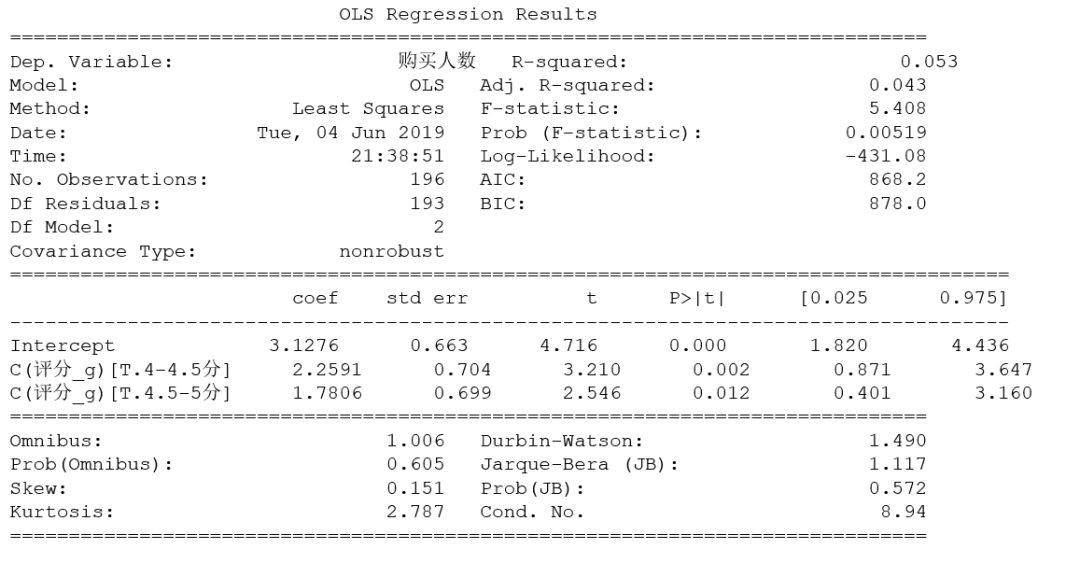
图5 参数估计结果
模型的结果我们需要以下几个方面去解读：
1）Coef列：此列中缺失了C(评分_g)这一类中的“小于4分”，并不是说这类可以忽略，而是表示截距项（Intercept）的含义，也就是截距项表示评分区间在“小于4分”这一类对“对数购买人数”的具体影响是：在该评分区间下，对数购买人数为3.1276。
2）对其他水平的解读：其他类的解读均以截距项为基准，表示了对因变量的影响相对于基准的差。比如：评分区间为“4-4.5分”的，这个水平的参数估计值为2.2591，表示与截距项相比，该水平下的对数购买人数增加了2.2591。其对应的P值0.002，表示这两个评分水平之间对对数购买人数有显著影响，该水平下对数购买人数具体为5.3867。
但是每次都这么手工计算会不会太麻烦，小编可是计算器都用上了啊。我们说强大的python肯定不会让我们每次都找计算器哒，早就帮助我们解决了，只需要在formula中的~右边加上“-1”。如例6。
例6 方差分析
formula='购买人数~C(评分_g)-1'
data_shop_est1=ols(formula,data_shop).fit()
print(data_shop_est1.summary())
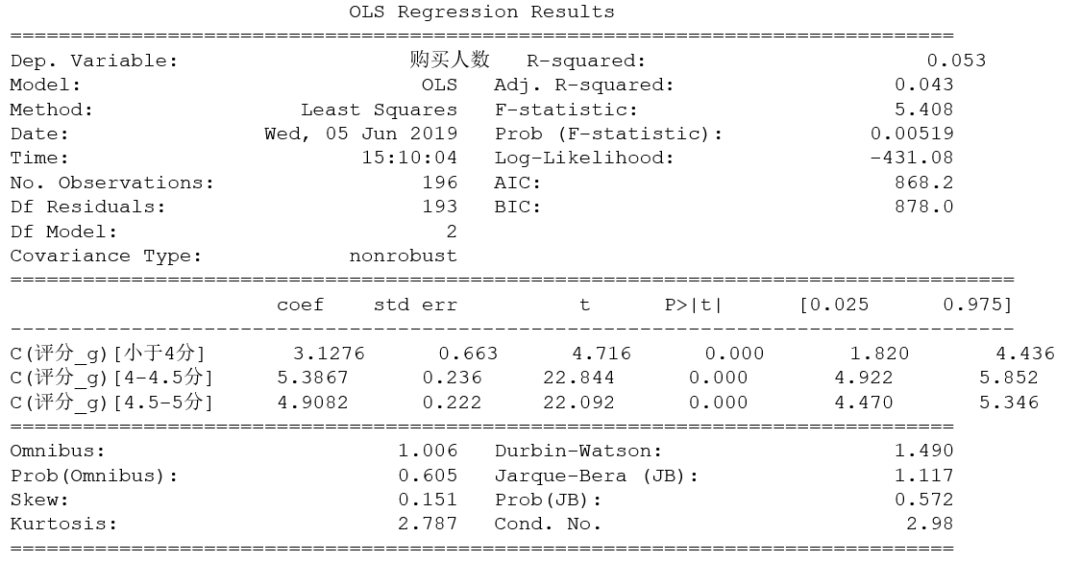
图6 方差分析结果
可以从结果看出，此时的评分中“4-4.5分”其参数估计的系数就是绝对数值5.3867，与手动计算出的一致。从结果可以看出，评分介于“4-4.5分”的购买人数最多，其次是“4.5-5分”，最少的是“小于4分”。
这时候有童鞋不禁会问，这个结论对于火锅和烧烤都适用吗？那么这就需要考虑两个或者两个以上的因素对购买人数的影响，这就需要利用多因素方差分析。
在多因素方差分析中，由于考虑的因素众多，这些因素不仅自己对因变量产生影响，它们值间也会共同对因变量产生影响，就跟流感的交叉感染似的。我们把因素单独对因变量产生的影响称为“主效应”。
在火锅的案例中，我们考虑不同的城市，不同的关键词（火锅、烧烤）对对数团购人数的影响，建立只有主效应的多因素方差分析。这里可以使用statsmodels中的anova_lm和ols进行分析。如例7。
例7 多因素方差分析
formula='购买人数~C(评分_g)+C(关键词)+C(城市)'
data_shop_anova1=sm.stats.anova_lm(ols(formula,data=data_shop).fit(),typ=3)
print(data_shop_anova1)
图7 方差分析结果
从结果可以看出，在0.05的显著性水平下，城市这个因素对因变量的影响不显著。但是关键词（火锅&烧烤）的P值=0.01，评分_g的P值=0.01，均通过了显著性检验。因此，在上段程序中的formula语句中去除城市这个变量，在只考虑关键词（火锅&烧烤）和评分_g的情况下，再做一次多因素方差分析。
例8 多因素方差分析
formula='购买人数~C(评分_g)+C(关键词)'
data_shop_anova2=sm.stats.anova_lm(ols(formula,data=data_shop).fit(),typ=3)
print(data_shop_anova2)
其结果如图8。
图8 多因素方差分析结果
从结果可以看出，评分_g和关键词对对数团购人数影响非常显著，说明大家在团购的时候，主要会考虑是烧烤还是火锅，还有店家的评分。
那么，究竟这些显著的影响因素中具体会对因变量产生如何的影响？下面我们做了模型的参数估计，如例9。
例9 参数估计
data_shop_anova1_set=ols(formula,data=data_shop).fit()
print(data_shop_anova1_set.summary())
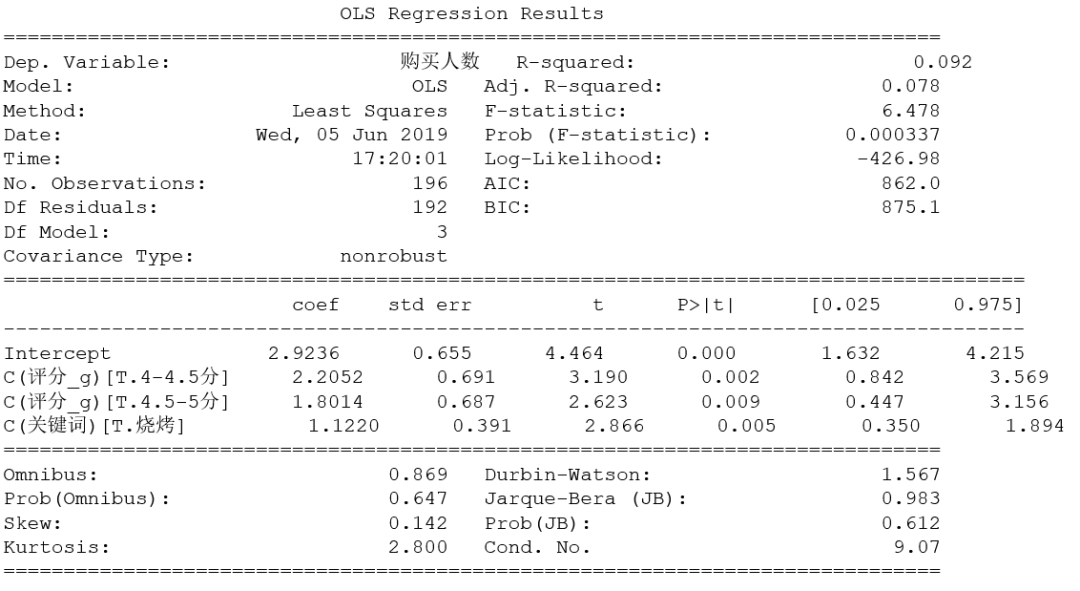图9 参数估计结果
从结果图9可以看出，评分在“小于4分”的火锅团购，其对数团购人数为2.9236。评分在“4-4.5分”的烧烤团购，其对数团购人数为2.9236+2.0252+1.1220=6.0708，具体为433人。
好了，今天就讲到这里。
