在处理宏观经济数据时,经常会遇到缺失值问题。在本文中,我们以固定资产投资价格指数为例,讨论填补缺失值的两种方法,及其Python实现。
通过简单分析原始数据,可以看到,固定资产投资价格指数,在1998年6月至2002年12月,是每半年发布一次。自2003年初至2019年12月,是每季度发布一次。我们希望获得月度的固定资产投资价格指数,从而对月度的固定资产投资数据进行价格折现。

一、插值法—scipy包的interpolate模块
scipy包的interpolate模块,可以使用线性或者二阶和三阶的样条曲线,对缺失值进行插补。插补分成两个步骤:
Python代码如下:
from scipy.interpolate import interp1d
# 提取有取值的样本
_FAIPriceIndex = FAIPriceIndex.reset_index()
x = np.array(_FAIPriceIndex[_FAIPriceIndex['M0012976'].notnull()].index)
y = np.array(_FAIPriceIndex[_FAIPriceIndex['M0012976'].notnull()]['M0012976'])
xnew = np.array(_FAIPriceIndex.index)
# 拟合插值函数
f1 = interp1d(x,y)
f2 = interp1d(x, y, kind='quadratic')
f3 = interp1d(x, y, kind='cubic')
# 对全序列插补
_FAIPriceIndex = pd.DataFrame([f1(xnew),f2(xnew),f3(xnew)]).T
_FAIPriceIndex = _FAIPriceIndex.set_index(FAIPriceIndex.index)
FAIPriceIndex = FAIPriceIndex.join(_FAIPriceIndex, how='outer')
FAIPriceIndex.columns = ['initial', 'linear', 'quadratic', 'cubic']
# 作图
FAIPriceIndex.iplot(mode=['markers','lines','lines','lines'],title='固定资产投资投资价格指数的插值法',
size=4,subplots=True,dimensions=(1000,600),subplot_titles=True,legend=False,shape=(2,2))
从插值的结果来看,线性、二阶和三阶样条函数,都可以比较好的对缺失值进行插补。
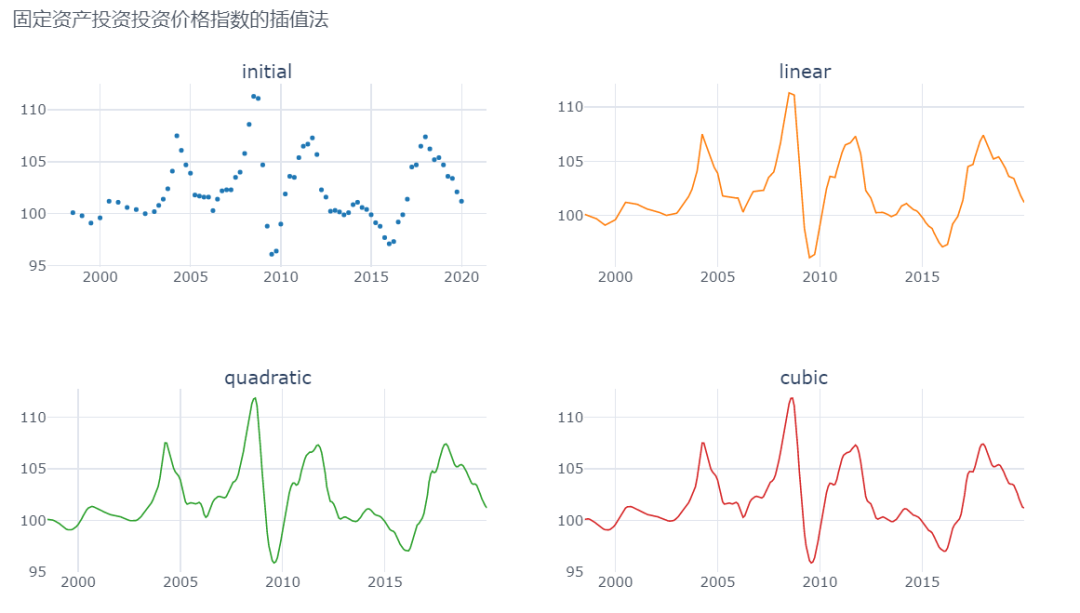
二、回归法—statsmodels包的OLS模块
如果我们可以获得其他高频变量的话,也可以通过回归法,对缺失值进行插补。从下图可以看到,PPI的频率更高,而且与固定资产投资价格指数的变动一致,可以作为自变量用于插补。

我们使用statsmodels包的OLS模块,建立回归模型,对缺失值进行插补。插补分成两个步骤:
Python代码如下:
import statsmodels.api as sm
y = FAIPriceIndex.iloc[:, 0] # 因变量为第 1 列数据
x = FAIPriceIndex.iloc[:, 1] # 自变量为第 2 列数据
x = sm.add_constant(x) # 若模型中有截距,必须有这一步
model = sm.OLS(y, x, missing='drop').fit() # 构建最小二乘模型并拟合
print(model.summary()) # 输出回归结果
从回归的拟合结果来看,PPI的回归系数为0.6,且显著不为零。整体模型的R方为65%,可以满足我们的需求。
OLS Regression Results
==============================================================================
Dep. Variable: M0012976 R-squared: 0.656
Model: OLS Adj. R-squared: 0.651
Method: Least Squares F-statistic: 144.8
Date: Tue, 05 Jan 2021 Prob (F-statistic): 2.80e-19
Time: 15:59:44 Log-Likelihood: -157.98
No. Observations: 78 AIC: 320.0
Df Residuals: 76 BIC: 324.7
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 42.5011 4.976 8.542 0.000 32.591 52.411
M0001209 0.5903 0.049 12.033 0.000 0.493 0.688
==============================================================================
Omnibus: 0.844 Durbin-Watson: 0.452
Prob(Omnibus): 0.656 Jarque-Bera (JB): 0.900
Skew: 0.234 Prob(JB): 0.638
Kurtosis: 2.761 Cond. No. 2.40e+03
==============================================================================
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
predicts = model.predict(x) # 模型的预测值
predicts.name = 'ols'
FAIPriceIndex = FAIPriceIndex.join(predicts,how='outer')
FAIPriceIndex.columns = ['initial', 'ppi', 'ols']
FAIPriceIndex.iplot(dimensions=(1000,600),title='固定资产投资投资价格指数的回归法',
mode=['markers','lines','lines'],size=4)
从回归法的插补结果来看,OLS方法可以很好的捕捉到回归自变量PPI的变动,但是并不是强制通过原始数据点,在部分时间段,与原始的固定资产投资价格指数,产生了较为明显的偏离。

三、两种方法的简单比较
我们把两种方法的结果做对比如下,从下图可以看到,两种方法所获得的插值,都可以较好的捕捉源数据的趋势,其中interpolate插值法,严格契合原数据,但是中间的插值并没有基于额外的信息。而回归法,较好的纳入了PPI的信息,但是对原数据并没有完美契合。
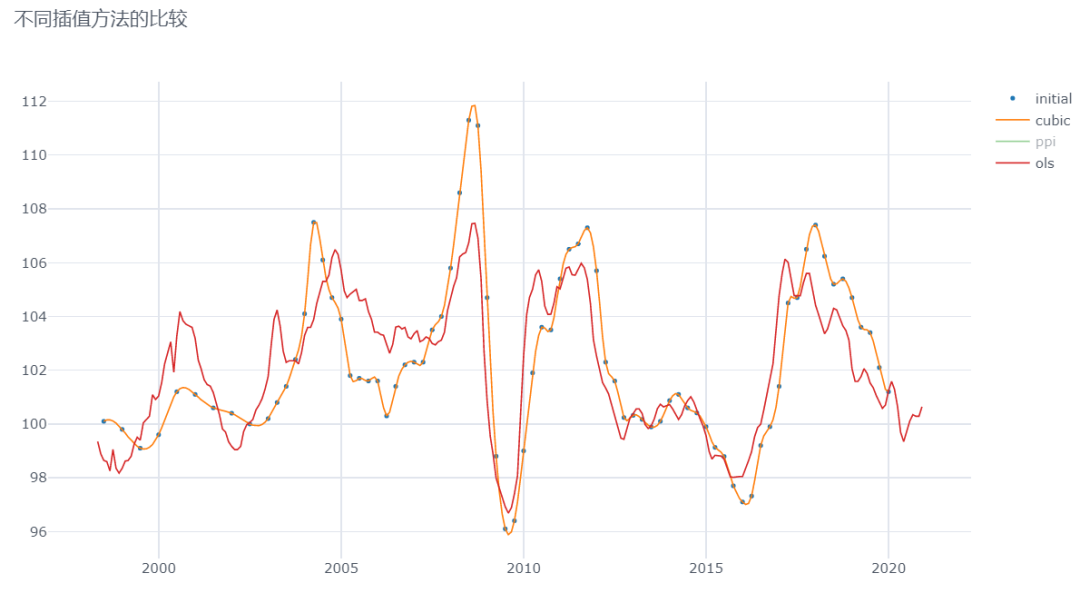
另一方面,interpolate插值法,对样本外数据的插值并不理想。比如固定资产投资价格指数,2020年后并没有发布,我们试图对样本外进行插值,如下图所示,插值效果比较差。

从笔者个人实践上看,interpolate插值法基本上够用,但是如果需要样本外插值,可以结合回归法进行外推。