机器学习算法-随机森林之理论概述
表达数据集来源于 https://file.biolab.si/biolab/supp/bi-cancer/projections/。
为了展示随机森林的能力,我们用一套早期的淋巴瘤基因表达芯片数据集,包含77个样品,2个分组和7070个变量。
读入数据
expr_file metadata_file
# 每个基因表达值是内部比较,只要是样品之间标准化的数据即可,其它什么转换都关系不大
expr_mat
metadata
dim(expr_mat)
## [1] 7070 77
基因表达表
expr_mat[1:4,1:5]
## DLBCL_1 DLBCL_2 DLBCL_3 DLBCL_4 DLBCL_5
## A28102 -1 25 73 267 16
## AB000114_at -45 -17 91 41 24
## AB000115_at 176 531 257 202 187
## AB000220_at 97 353 80 138 39
Metadata表
head(metadata)
## class
## DLBCL_1 DLBCL
## DLBCL_2 DLBCL
## DLBCL_3 DLBCL
## DLBCL_4 DLBCL
## DLBCL_5 DLBCL
## DLBCL_6 DLBCL
样品筛选和排序
对读入的表达数据进行转置。通常我们是一行一个基因,一列一个样品。在构建模型时,数据通常是反过来的,一列一个基因,一行一个样品。每一列代表一个变量
(variable),每一行代表一个案例
(case)。这样更方便提取每个变量,且易于把模型中的x,y放到一个矩阵中。
样本表和表达表中的样本顺序对齐一致也是需要确保的一个操作。
# 表达数据转置
# 习惯上我们是一行一个基因,一列一个样品
# 做机器学习时,大部分数据都是反过来的,一列一个基因,一行一个样品
# 每一列代表一个变量
expr_mat expr_mat_sampleL metadata_sampleL
common_sampleL
# 保证表达表样品与METAdata样品顺序和数目完全一致
expr_mat metadata
判断是分类还是回归
# R4.0之后默认读入的不是factor,需要做一个转换
# devtools::install_github("Tong-Chen/YSX")
library(YSX)
# 此处的class根据需要修改
group = "class"
# 如果group对应的列为数字,转换为数值型 - 做回归
# 如果group对应的列为分组,转换为因子型 - 做分类
if(numCheck(metadata[[group]])){
if (!is.numeric(metadata[[group]])) {
metadata[[group]] }
} else{
metadata[[group]] }
随机森林初步分析
library(randomForest)
# 查看参数是个好习惯
# 有了前面的基础概述,再看每个参数的含义就明确了很多
# 也知道该怎么调了
# 每个人要解决的问题不同,通常不是别人用什么参数,自己就跟着用什么参数
# 尤其是到下游分析时
# ?randomForest
加载包之后,直接分析一下,看到结果再调参。(竟然被awk生成的随机数给整蒙了,也谈随机数生成种子)
# 设置随机数种子,具体含义见 https://mp.weixin.qq.com/s/6plxo-E8qCdlzCgN8E90zg
set.seed(304)
# 直接使用默认参数
rf 查看下初步结果,
随机森林类型判断为分类,构建了500棵树,每次决策时使用了84个基因,OOB估计的错误率是12.99%,挺高的。
分类效果评估矩阵Confusion matrix,显示DLBCL组的分类错误率为0.034,FL组的分类错误率为0.42。这是随机森林的默认操作,样本量多的分类错误率会低
(后面我们再调整)。
rf
##
## Call:
## randomForest(x = expr_mat, y = metadata$class)
## Type of random forest: classification
## Number of trees: 500
## No. of variables tried at each split: 84
##
## OOB estimate of error rate: 12.99%
## Confusion matrix:
## DLBCL FL class.error
## DLBCL 56 2 0.03448276
## FL 8 11 0.42105263
随机森林参数调试 - 决策树的数目
增加决策树的数目到1000测试下分类率是否会降低。OOB估计的错误率是11.69%,还是不低。
分类效果评估矩阵Confusion matrix,显示DLBCL组的分类错误率为0.017,FL
组的分类错误率为0.42。也都略有降低。
set.seed(304)
rf1000 rf1000
##
## Call:
## randomForest(x = expr_mat, y = metadata$class, ntree = 1000)
## Type of random forest: classification
## Number of trees: 1000
## No. of variables tried at each split: 84
##
## OOB estimate of error rate: 11.69%
## Confusion matrix:
## DLBCL FL class.error
## DLBCL 57 1 0.01724138
## FL 8 11 0.42105263
增加决策树的数目到2000测试下分类率是否会降低。OOB估计的错误率是11.69%没有变化。
分类效果评估矩阵Confusion matrix,显示DLBCL组的分类错误率为0.017,FL组的分类错误率为0.42。FL组样品量少,分类效果还是不好。
set.seed(304)
rf2000 rf2000
##
## Call:
## randomForest(x = expr_mat, y = metadata$class, ntree = 2000)
## Type of random forest: classification
## Number of trees: 2000
## No. of variables tried at each split: 84
##
## OOB estimate of error rate: 11.69%
## Confusion matrix:
## DLBCL FL class.error
## DLBCL 57 1 0.01724138
## FL 8 11 0.42105263
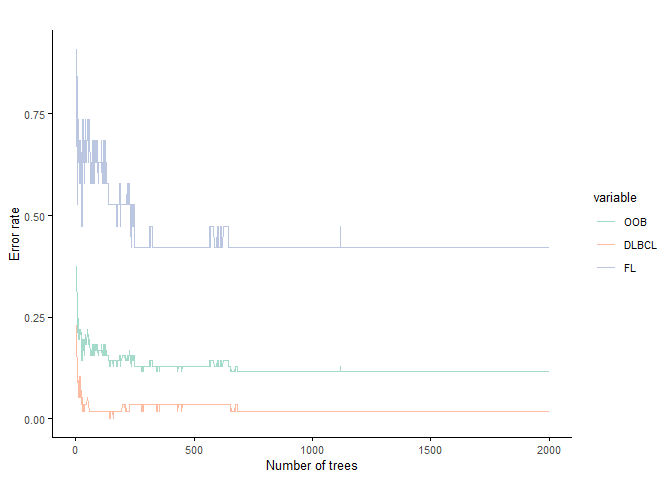
绘制下从第1到2000棵树时,OOB的变化趋势是怎样的?从这张图可以看到,600棵树之后,基本没有影响了。
library(ggplot2)
YSX::sp_lines(as.data.frame(rf2000$err.rate), manual_color_vector="Set2",
x_label="Number of trees", y_label="Error rate",line_size=0.6,
width=6, height=4
)
随机森林参数调试 - 用于决策的变量的数目 (m)
影响随机森林的第二个参数(m):
构建每棵决策树时随机抽取的变量的数目。(假设你已阅读过了机器学习算法-随机森林之理论概述)。在randomForest函数中有一个参数mtry
即是做这个的。在处理分类问题时,其默认值为sqrt(p);处理回归问题时,其默认值为p/3;p是总的变量数目。
我们先人工测试几个不同的mtry看下效果。mtry=20时错误率为15.58%。
# 增加树的数目没有给出好的结果,这里还是用的默认的500棵树以便获得较快的运行速度
set.seed(304)
rf_mtry20 rf_mtry20
##
## Call:
## randomForest(x = expr_mat, y = metadata$class, mtry = 20)
## Type of random forest: classification
## Number of trees: 500
## No. of variables tried at each split: 20
##
## OOB estimate of error rate: 15.58%
## Confusion matrix:
## DLBCL FL class.error
## DLBCL 57 1 0.01724138
## FL 11 8 0.57894737
我们先人工测试几个不同的mtry看下效果。mtry=50时错误率为11.69%(默认使用了84个变量,准确率为12.99)。
# 增加树的数目没有给出好的结果,这里还是用的默认的500棵树以便获得较快的运行速度
set.seed(304)
rf_mtry50 rf_mtry50
##
## Call:
## randomForest(x = expr_mat, y = metadata$class, mtry = 50)
## Type of random forest: classification
## Number of trees: 500
## No. of variables tried at each split: 50
##
## OOB estimate of error rate: 11.69%
## Confusion matrix:
## DLBCL FL class.error
## DLBCL 57 1 0.01724138
## FL 8 11 0.42105263
我们先人工测试几个不同的mtry看下效果。mtry=100时错误率为11.69%。
# 增加树的数目没有给出好的结果,这里还是用的默认的500棵树以便获得较快的运行速度
set.seed(304)
rf_mtry100 rf_mtry100
##
## Call:
## randomForest(x = expr_mat, y = metadata$class, mtry = 100)
## Type of random forest: classification
## Number of trees: 500
## No. of variables tried at each split: 100
##
## OOB estimate of error rate: 11.69%
## Confusion matrix:
## DLBCL FL class.error
## DLBCL 57 1 0.01724138
## FL 8 11 0.42105263
一个个测试也不是办法,tuneRF给我们提供了一个根据OOB值迭代鉴定最合适的mtry值的函数。(测试几次,不太好用,改一个stepfactor,结果变化很大)
# mtryStart: 从多少个变量开始尝试,可用默认值。程序会自动向更多变量或更少变量迭代。
# ntreeTry: 迭代时构建多少棵树,这里设置为500,与我们上面获得的效果比较好的树一致。
# stepFactor: 迭代步长,mtryStart向更多变量迭代时乘以此值;mtryStart向更少变量迭代时除以此值。
# improve:如果迭代不能给OOB带来给定值的改善,则停止迭代。
set.seed(304)
tuneRF(expr_mat, metadata$class, ntreeTry=500, stepFactor=1.1, improve=1e-5)
## mtry = 84 OOB error = 12.99%
## Searching left ...
## mtry = 77 OOB error = 10.39%
## 0.2 1e-05
## mtry = 70 OOB error = 11.69%
## -0.125 1e-05
## Searching right ...
## mtry = 92 OOB error = 11.69%
## -0.125 1e-05
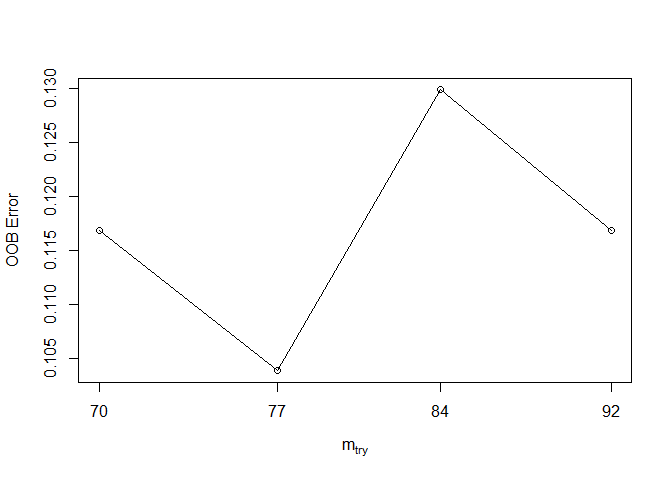
## mtry OOBError
## 70.OOB 70 0.1168831
## 77.OOB 77 0.1038961
## 84.OOB 84 0.1298701
## 92.OOB 92 0.1168831
randomForest自带了另一个函数rfcv,通过嵌套交叉验证方式评估了根据变量重要性降低预测变量后的模型的性能。
result = rfcv(expr_mat, metadata$class, cv.fold=10)
result$error.cv
## 7070 3535 1768 884 442 221 110 55 28 14 7
## 0.10389610 0.11688312 0.10389610 0.09090909 0.09090909 0.09090909 0.09090909 0.10389610 0.10389610 0.12987013 0.14285714
## 3 1
## 0.15584416 0.15584416
后面我们详细讲下交叉验证这个最常用的评估模型的方法。
往期精品(点击图片直达文字对应教程)
后台回复“生信宝典福利第一波”或点击阅读原文获取教程合集



(请备注姓名-学校/企业-职务等)