9.2.2 MobileNet V2
MobileNet V2 创新性的提出了具有线性bottleneck 的Inverted 残差块。
这种块特别适用于移动设备和嵌入式设备,因为它用到的张量都较小,因此减少了推断期间的内存需求。
9.2.2.1 线性bottleneck
一直以来,人们认为与任务相关的信息是嵌入到feature map 中的一个低维子空间。因此feature map 事实上有一定的信息冗余。如果缩减feature map 的通道数量(相当于降维),则可以降低计算量。
MobileNet V1 就是采用宽度乘子,从而在计算复杂度和准确率之间平衡。
由于ReLU 非线性激活的存在,缩减输入 feature map 的通道数量可能会产生不良的影响。
输入feature map 中每个元素值代表某个特征,将所有图片在该feature map 上的取值扩成为矩阵:
其中 N 为样本的数量, 。即:行索引代表样本,列索引代表特征。所有特征由feature map 展平成一维得到。
通常 ,则输入矩阵 的秩 。
其中 , 为输出通道数。
上面的讨论的是 ReLU 的非线性导致信息的不可逆丢失。
对于输出的维度 ,如果 在维度 j 上的取值均小于 0 ,则由于 ReLU 的作用, 在维度 j 上取值均为 0 ,此时可能发生信息不可逆的丢失。
如果 1x1 卷积的输出通道数很小(即 较小),使得 ,则 的每个维度都非常重要。
一旦经过 ReLU 之后 的信息有效维度降低(即 ),则发生信息的丢失。且这种信息丢失是不可逆的。
这使得输出feature map 的有效容量降低,从而降低了模型的表征能力。
如果 1x1 卷积的输出通道数非常小,使得 ,则信息压缩的过程中就发生信息不可逆的丢失。
- 如果考虑
ReLU,则输出 featuremap 为: - 对于
1x1 卷积(不考虑ReLU),则1x1 卷积是输入特征的线性组合。输出 featuremap 以矩阵描述为:
实验表明:bootleneck 中使用线性是非常重要的。
虽然引入非线性会提升模型的表达能力,但是引入非线性会破坏太多信息,会引起准确率的下降。在Imagenet 测试集上的表现如下图:

9.2.2.2 bottleneck block
bottleneck block:输入feature map 首先经过线性 bottleneck 来扩张通道数,然后经过深度可分离卷积,最后通过线性bottleneck 来缩小通道数。
输入bootleneck 输出通道数与输入通道数的比例称作膨胀比。
- 通常较小的网络使用略小的膨胀比效果更好,较大的网络使用略大的膨胀比效果更好。
- 如果膨胀比小于 1 ,这就是一个典型的
resnet 残差块。
可以在 bottleneck block 中引入旁路连接,这种bottleneck block 称作Inverted 残差块,其结构类似ResNet 残差块。
在ResNeXt 残差块中,首先对输入feature map 执行1x1 卷积来压缩通道数,最后通过1x1 卷积来恢复通道数。这对应了一个输入 feature map 通道数先压缩、后扩张的过程。
在Inverted 残差块中,首先对输入feature map 执行1x1 卷积来扩张通道数,最后通过1x1 卷积来恢复通道数。这对应了一个输入 feature map 通道数先扩张、后压缩的过程。这也是Inverted 残差块取名为Inverted 的原因。
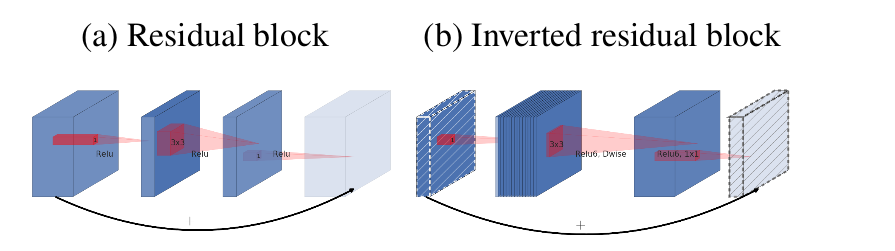
当深度可分离卷积的步长为 1 时,bottleneck block包含了旁路连接。
当深度可分离卷积的步长不为 1 时,bottleneck block
不包含旁路连接。这是因为:输入feature map 的尺寸与块输出feature map 的尺寸不相同,二者无法简单拼接。
虽然可以将旁路连接通过一个同样步长的池化层来解决,但是根据ResNet的研究,破坏旁路连接会引起网络性能的下降。
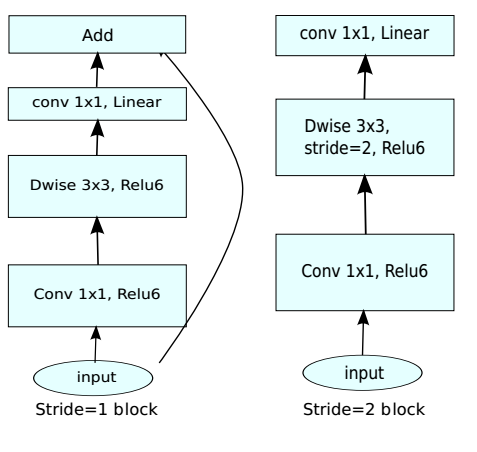
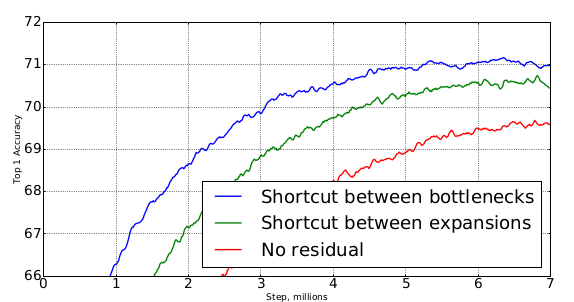
4.事实上旁路连接有两个插入的位置:在两个1x1 卷积的前后,或者在两个Dwise 卷积的前后。
通过实验证明:在两个1x1 卷积的前后使用旁路连接的效果最好。在Imagenet 测试集上的表现如下图:
5.bottleneck block 可以看作是对信息的两阶段处理过程:
在MobileNet v2 中这二者是独立的,而传统网络中这二者是相互纠缠的。
- 阶段一:对输入
feature map 进行降维,这一部分代表了信息的容量。 - 阶段二:对信息进行非线性处理,这一部分代表了信息的表达。
9.2.2.3 网络性能
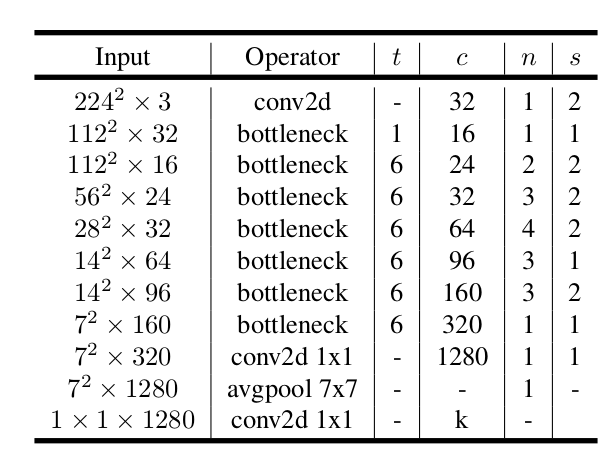
MobileNet V2 的设计基于 MobileNet v1 ,其结构如下:
每一行代表一个或者一组相同结构的层,层的数量由 n 给定。
同一行内的层的类型相同,由Operator 指定。其中bottleneck 指的是bottleneck block 。
同一行内的层:第一层采用步幅s,其它层采用步幅1 。
采用ReLU6 激活函数,因为它在低精度浮点运算的环境下表现较好。
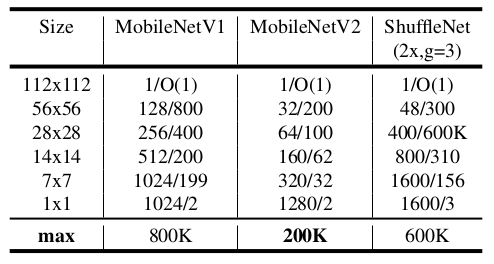
与MobileNet V1 类似,MobileNet V2 也可以引入宽度乘子、分辨率乘子这两个超参数。
网络推断期间最大内存需求(通道数/内存消耗(Kb)):采用 16 bit 的浮点运算。
4.网络在ImageNet 测试集上的表现:
| 网络 | Top 1 | Params(百万) | 乘-加 数量(百万) | CPU |
|---|
| MobileNet V1 | 70.6 | 4.2 | 575 | 113ms |
| ShuffleNet (1.5) | 71.5 | 3.4 | 292 | - |
| ShuffleNet (x2) | 73.7 | 5.4 | 524 | - |
| NasNet-A | 74.0 | 5.3 | 564 | 183ms |
| MobileNet V2 | 72.0 | 3.4 | 300 | 75ms |
| MobileNet V2(1.4) | 74.7 | 6.9 | 585 | 143ms |
9.3 ShuffleNet 系列
9.3.1 ShuffleNet
-
ShuffleNet 提出了 1x1分组卷积+通道混洗 的策略,在保证准确率的同时大幅降低计算成本。
ShuffleNet 专为计算能力有限的设备(如:10~150MFLOPs)设计。在基于ARM 的移动设备上,ShuffleNet 与AlexNet 相比,在保持相当的准确率的同时,大约 13 倍的加速。
9.3.1.1 ShuffleNet block
在Xception 和ResNeXt 中,有大量的1x1 卷积,所以整体而言1x1 卷积的计算开销较大。如ResNeXt 的每个残差块中,1x1 卷积占据了乘-加运算的 93.4% (基数为32时)。
在小型网络中,为了满足计算性能的约束(因为计算资源不够)需要控制计算量。虽然限制通道数量可以降低计算量,但这也可能会严重降低准确率。
解决办法是:对1x1 卷积应用分组卷积,将每个 1x1 卷积仅仅在相应的通道分组上操作,这样就可以降低每个1x1 卷积的计算代价。
1x1 卷积仅在相应的通道分组上操作会带来一个副作用:每个通道的输出仅仅与该通道所在分组的输入(一般占总输入的比例较小)有关,与其它分组的输入(一般占总输入的比例较大)无关。这会阻止通道之间的信息流动,降低网络的表达能力。
解决办法是:采用通道混洗,允许分组卷积从不同分组中获取输入。
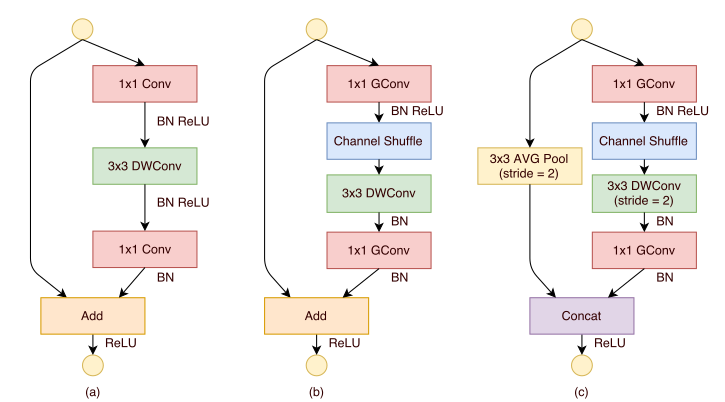
- 如下图所示:
(a) 表示没有通道混洗的分组卷积;(b) 表示进行通道混洗的分组卷积;(c) 为(b) 的等效表示。 - 由于通道混洗是可微的,因此它可以嵌入到网络中以进行端到端的训练。
ShuffleNet 块的结构从ResNeXt 块改进而来:下图中(a) 是一个ResNeXt
块,(b) 是一个 ShuffleNet 块,(c) 是一个步长为2 的 ShuffleNet 块。
在 ShuffleNet 块中:
因为当feature map 减半时,为了缓解信息丢失需要将输出通道数加倍从而保持模型的有效容量。
第一个1x1 卷积替换为1x1 分组卷积+通道随机混洗。
第二个1x1 卷积替换为1x1 分组卷积,但是并没有附加通道随机混洗。这是为了简单起见,因为不附加通道随机混洗已经有了很好的结果。
在3x3 depthwise 卷积之后只有BN 而没有ReLU 。
恒等映射直连替换为一个尺寸为 3x3 、步长为2 的平均池化。
将残差部分与直连部分的feature map 拼接,而不是相加。
9.3.1.2 网络性能
在Shufflenet 中,depthwise 卷积仅仅在1x1 卷积的输出 feature map 上执行。这是因为 depthwise 很难在移动设备上高效的实现,因为移动设备的 计算/内存访问 比率较低,所以仅仅在1x1
卷积的输出 feature map 上执行从而降低开销。
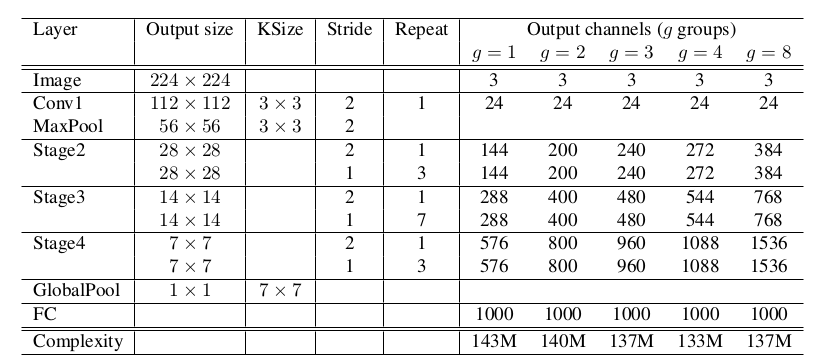
ShuffleNet 网络由ShuffleNet 块组成。
每个Stage 的第一个块的步长为 2 ,stage 内的块在其它参数上相同。
在 Stage2 的第一个1x1 卷积并不执行分组卷积,因此此时的输入通道数相对较小。
每个ShuffleNet 块中的第一个1x1 分组卷积的输出通道数为:该块的输出通道数的 1/4 。
使用较少的数据集增强,因为这一类小模型更多的是遇到欠拟合而不是过拟合。
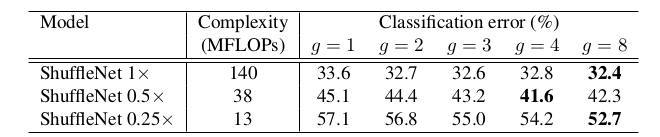
复杂度给出了计算量(乘-加运算),KSize 给出了卷积核的尺寸,Stride 给出了ShuffleNet block 的步长,Repeat 给出了 ShuffleNet block 重复的次数,g 控制了ShuffleNet block 分组的数量。g=1 时,1x1 的通道分组卷积退化回原始的1x1 卷积。
超参数 g 会影响模型的准确率和计算量。在 ImageNet
测试集上的表现如下:
ShuffleNet sx 表示对ShuffleNet 的通道数增加到 s 倍。这通过控制 Conv1 卷积的输出通道数来实现。
g 越大,则计算量越小,模型越准确。
其背后的原理是:小模型的表达能力不足,通道数量越大,则小模型的表达能力越强。
g 越大,则准确率越高。这是因为对于ShuffleNet,分组越大则生成的feature map 通道数量越多,模型表达能力越强。* 网络的通道数越小(如ShuffleNet 0.25x ),则这种增益越大。
随着分组越来越大,准确率饱和甚至下降。
这是因为随着分组数量增大,每个组内的通道数量变少。虽然总体通道数增加,但是每个分组提取有效信息的能力变弱,降低了模型整体的表征能力。
虽然较大g 的ShuffleNet 通常具有更好的准确率。但是由于它的实现效率较低,会带来较大的推断时间。
通道随机混洗的效果要比不混洗好。在 ImageNet 测试集上的表现如下:
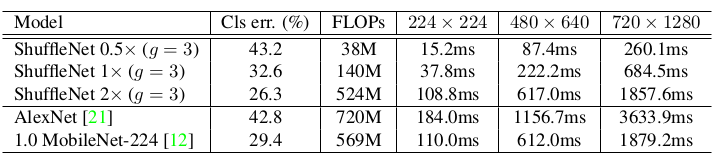
多种模型在ImageNet 测试集上的表现:
比较分为三组,每一组都有相差无几的计算量。 给出了在该组中,模型相对于 MobileNet 的预测能力的提升。
MFLOPs 表示乘-加运算量(百万),错误率表示top-1 error 。ShuffleNet 0.5x(shallow,g=3) 是一个更浅的ShuffleNet 。考虑到MobileNet 只有 28 层,而ShuffleNet 有 50 层,因此去掉了Stage 2-4 中一半的块,得到一个教浅的、只有 26 层的 ShuffleNet 。
在移动设备上的推断时间(Qualcomm Snapdragon 820 processor,单线程):
9.3.2 ShuffleNet V2
ShuffleNet V2 基于一系列对照实验提出了高效网络设计的几个通用准则,并提出了ShuffleNet V2 的网络结构。
9.3.2.1 小型网络通用设计准则
目前衡量模型推断速度的一个通用指标是FLOPs(即乘-加 计算量)。事实上这是一个间接指标,因为它不完全等同于推断速度。如:MobileNet V2 和 NASNET-A 的FLOPs 相差无几,但是MobileNet V2 的推断速度要快得多。
如下所示为几种模型在GPU 和ARM 上的准确率(在ImageNet 验证集上的测试结果)、模型推断速度(通过Batch/秒来衡量)、计算复杂度(通过FLOPs 衡量)的关系。
在ARM 平台上batchsize=1
, 在GPU 平台上batchsize=8 。
准确率与模型容量成正比,而模型容量与模型计算复杂度成成比、计算复杂度与推断速度成反比。因此:模型准确率越高,则推断速度越低;模型计算复杂度越高,则推断速度越低。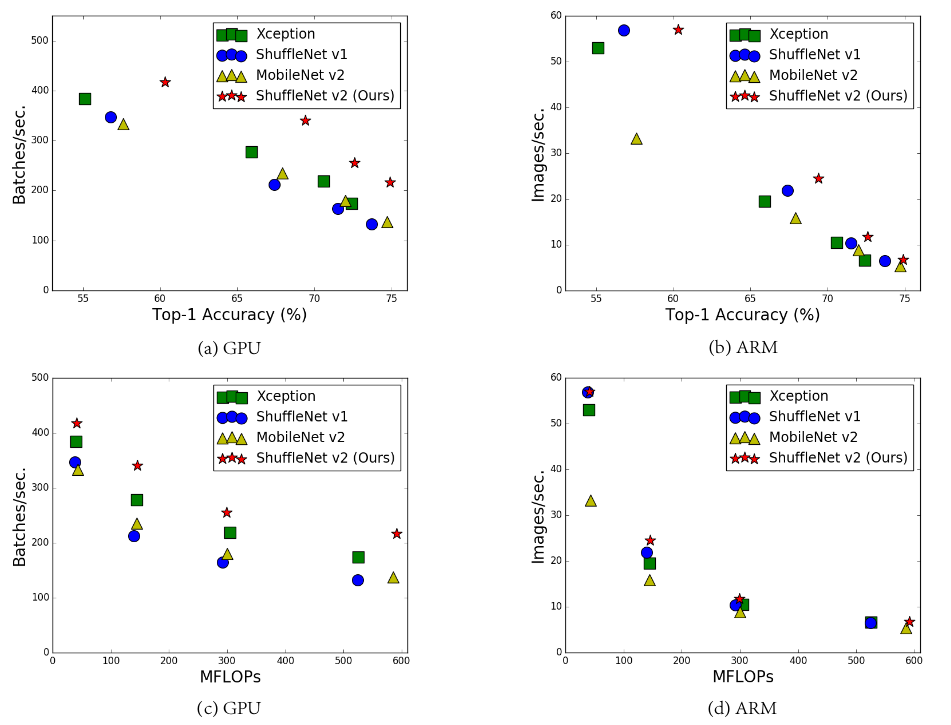
除了FLOPs 之外,还有几个因素对推断速度有重要的影响。
内存访问量(memory access cost:MAC):在某些操作(如分组卷积)中,其时间开销占相当大比例。因此它可能是GPU 这种具有强大计算能力设备的瓶颈。
模型并行度:相同FLOPs 的情况下,高并行度的模型比低并行度的模型快得多。
即使相同的操作、相同的 FLOPs,在不同的硬件设备上、不同的库上,其推断速度也可能不同。
MobileNet V2 和 ShuffleNet V1 这两个网络非常具有代表性,它们分别采用了group 卷积和 depth-wise 卷积。这两个操作广泛应用于其它的先进网络。
利用实验分析它们的推断速度(以推断时间开销来衡量)。其中:宽度乘子均为1,ShuffleNet V1 的分组数g=3。
从实验结果可知:FLOPs 指标仅仅考虑了卷积部分的计算量。虽然这部分消耗时间最多,但是其它操作包括数据IO、数据混洗、逐元素操作(ReLU、逐元素相加)等等时间开销也较大。
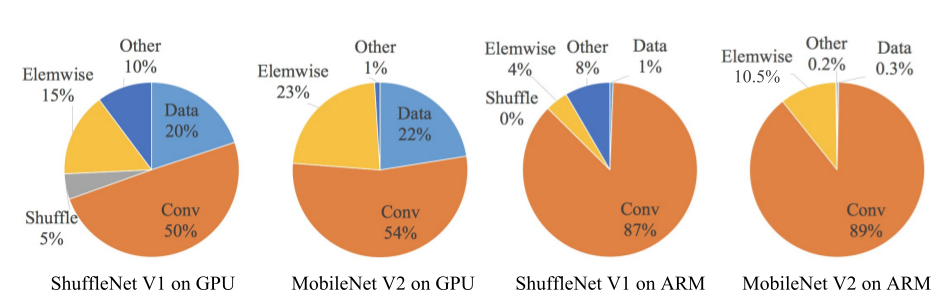
4.小型网络通用设计准则:
准则二:大量使用分组卷积会增加MAC 。分组卷积可以降低FLOPs 。换言之,它可以在FLOPs 固定的情况下,增大featuremap 的通道数从而提高模型的容量。但是采用分组卷积可能增加MAC 。对于1x1 卷积,设分组数为 g ,则FLOPs 数为 ,内存访问量为
当 时, 最小。因此 MAC 随着 g 的增加而增加。
准则三:网络分支会降低并行度。虽然网络中采用分支(如Inception系列、ResNet系列)有利于提高模型的准确率,但是它对GPU 等具有高并行计算能力的设备不友好,因此会降低计算效率。另外它还带来了卷积核的lauching以及计算的同步等问题,这也是推断时间的开销。
准则四:不能忽视元素级操作的影响。元素级操作包括ReLU、AddTensor、AddBias 等,它们的FLOPs 很小但是 MAC 很大。在ResNet 中,实验发现如果去掉ReLU 和旁路连接,则在GPU 和 ARM 上大约有 20% 的推断速度的提升。
9.3.2.2 ShuffleNet V2 block
ShuffleNet V1 block 的分组卷积违反了准则二,1x1 卷积违反了准则一,旁路连接的元素级加法违反了准则四。而ShuffleNet V2 block 修正了这些违背的地方。
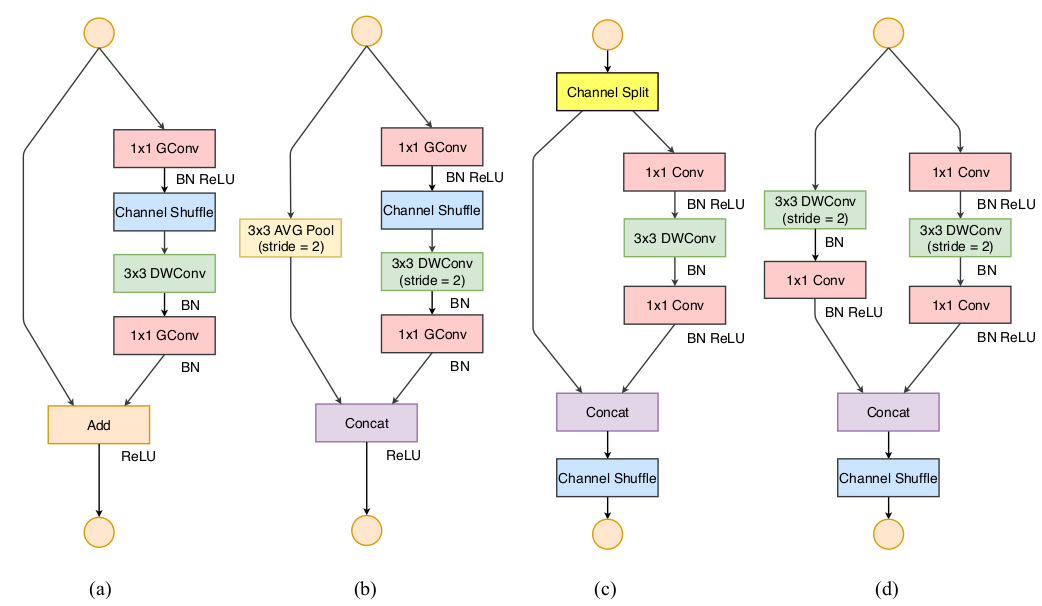
ShuffleNet V2 block 在 ShuffleNet V1 block 的基础上修改。(a),(b) 表示ShuffleNet V1 block (步长分别为1、2),(c),(d) 表示ShuffleNet V2 block (步长分别为1、2)。其中GConv 表示分组卷积,DWConv 表示depthwise 卷积。
当步长为1 时,ShuffleNet V2 block 首先将输入feature map 沿着通道进行拆分。设输入通道数为 ,则拆分为 和 。
根据准则三,左路分支保持不变,右路分支执行各种卷积操作。
根据准则二,右路的两个1x1 卷积不再是分组卷积,而是标准的卷积操作。因为分组已经由通道拆分操作执行了。
根据准则四,左右两路的featuremap 不再执行相加,而是执行特征拼接。可以将Concat、Channel Shuffle、Channel Split 融合到一个element-wise 操作中,这可以进一步降低element-wise 的操作数量。
当步长为2时,ShuffleNet V2 block 不再拆分通道,因为通道数量需要翻倍从而保证模型的有效容量。
在执行通道Concat 之后再进行通道混洗,这一点也与ShuffleNet V1 block 不同。
9.3.2.3 网络性能
ShuffleNet V2 的网络结构类似ShuffleNet V1,主要有两个不同:
- 用
ShuffleNet v2 block 代替 ShuffleNet v1 block 。 - 在
Global Pool 之前加入一个 1x1 卷积。
ShuffleNet V2 可以结合SENet 的思想,也可以增加层数从而由小网络变身为大网络。
下表为几个模型在ImageNet 验证集上的表现(single-crop)。

3.ShuffleNet V2 和其它模型的比较:
- 根据计算复杂度分成
40,140,300,500+ 等四组,单位:MFLOPs 。 - 准确率指标为模型在
ImageNet 验证集上的表现(single-crop)。 GPU 上的 batchsize=8,ARM 上的batchsize=1 。- 默认图片尺寸为
224x224,标记为* 的图片尺寸为160x160,标记为** 的图片尺寸为192x192 。
4.ShuffleNet V2 准确率更高。有两个原因:
但是ShuffleNet v2 block 在特征Concat 之后又执行通道混洗,这又不同于DenseNet 。
ShuffleNet V2 block 的构建效率更高,因此可以使用更多的通道从而提升模型的容量。
在每个ShuffleNet V2 block ,有一半通道的数据( )直接进入下一层。这可以视作某种特征重用,类似于DenseNet 。
9.4 IGCV 系列
设计小型化网络目前有两个代表性的方向,并且都取得了成功:
- 通过一系列低秩卷积核(其中间输出采用非线性激活函数)去组合成一个线性卷积核或者非线性卷积核。如用
1x3 +3x1 卷积去替代3x3 卷积 。 - 使用一系列稀疏卷积核去组成一个密集卷积核。如:交错卷积中采用一系列分组卷积去替代一个密集卷积。
9.4.1 IGCV
简化神经网络结构的一个主要方法是消除结构里的冗余。目前大家都认为现在深度神经网络结构里有很强的冗余性。
冗余可能来自与两个地方:
IGCV 通过研究卷积核通道方向的冗余,从而减少网络的冗余性。
- 卷积核空间方向的冗余。通过小卷积核替代(如,采用
3x3、1x3、3x1 卷积核)可以降低这种冗余。 - 卷积核通道方向的冗余。通过分组卷积、
depth-wise 卷积可以降低这种冗余。
事实上解决冗余性的方法有多种:
除了将卷积核进行二元化或者整数化之外,也可以将 feature map 进行二元化/整数化。
卷积核低秩分解:将大卷积核分解为两个小卷积核 ,如:将100x100 分解为 100x10 和10x100、将5x5 分解为两个3x3 。
稀疏卷积分解:将一个密集的卷积核分解为多个稀疏卷积核。如分组卷积、depth-wise 卷积。
二元化:将卷积核变成二值的-1 和+1,此时卷积运算的乘加操作变成了加减 操作。这样计算量就下降很多,存储需求也降低很多(模型变小)。
浮点数转整数:将卷积核的 32 位浮点数转换成16 位整数。此时存储需求会下降(模型变小)。
9.4.1.1 IGCV block
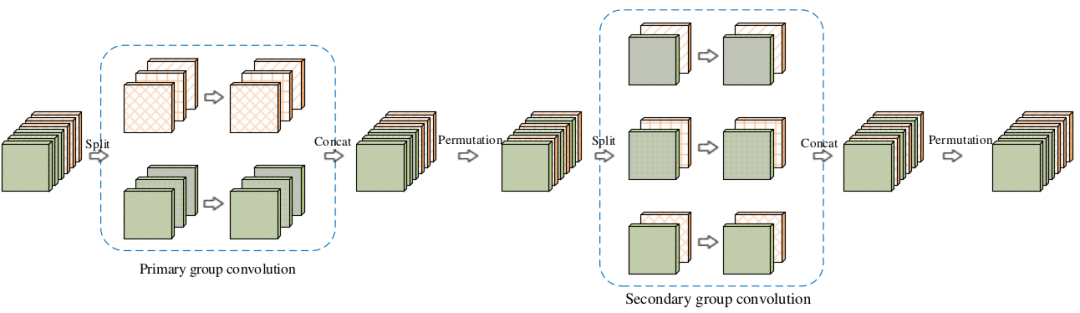
IGCV 提出了一种交错卷积模块,每个模块由相连的两层分组卷积组成,分别称作第一层分组卷积primary group conv 、第二层分组卷积secondary group conv 。
第一层分组卷积采用3x3 分组卷积,主要用于处理空间相关性;第二层分组卷积采用1x1 分组卷积,主要用于处理通道相关性。
每层分组卷积的每个组内执行的都是标准的卷积,而不是 depth-wise 卷积。
这两层分组卷积的分组是交错进行的。假设第一层分组卷积有 L 个分组、每个分组 M 个通道,则第二层分组卷积有 M 个分组、每个分组L 个通道。
第一层分组卷积中,同一个分组的不同通道会进入到第二层分组卷积的不同分组中。第二层分组卷积中,同一个分组的不同通道来自于第一层分组卷积的不同分组。
这两层分组卷积是互补的、交错的,因此称作交错卷积Interleaved Group Convolution:IGCV 。
这种严格意义上的互补需要对每层分组卷积的输出 feature map 根据通道数重新排列Permutation。这不等于混洗,因为混洗不能保证严格意义上的通道互补。
由于分组卷积等价于稀疏卷积核的常规卷积,该稀疏卷积核是block-diagonal (即:只有对角线的块上有非零,其它位置均为 0 )。
因此IGCV 块等价于一个密集卷积,该密集卷积的卷积核由两个稀疏的、互补的卷积核相乘得到。
假设第一层分组卷积的卷积核尺寸为 ,则 IGCV 块的参数数量为:
令 G=LM 为IGCV 块 的输入feature map 通道数量,则 。
对于常规卷积,假设卷积核的尺寸为 ,输入输出通道数均为 C,则参数数量为: 。当参数数量相等,即 时,则有: 。
当 时,有 。通常选择 ,考虑到 ,因此该不等式几乎总是成立。于是 IGCV 块总是比同样参数数量的常规卷积块更宽(即:通道数更多)。
在相同参数数量/计算量的条件下,IGCV 块(除了L=1 的极端情况)比常规卷积更宽,因此IGCV 块更高效。
采用IGCV 块堆叠而成的IGCV 网络在同样参数数量/计算量的条件下,预测能力更强。
Xception 块、带有加法融合的分组卷积块都是IGCV 块的特殊情况。
当 M=1,L 等于IGCV 块输入feature map 的输入通道数时,IGCV 块退化为Xception 块。
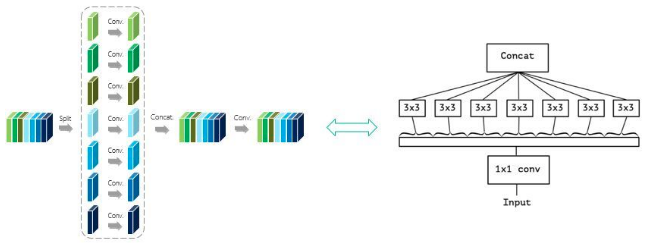
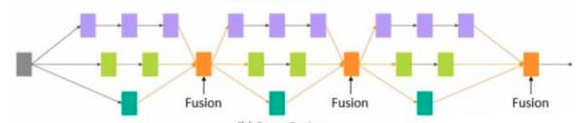
当 L=1,M 等于IGCV 块输入feature map 的输入通道数时,IGCV 块退化为采用Summation 融合的Deeply-Fused Nets block 。
9.4.1.2 网络性能
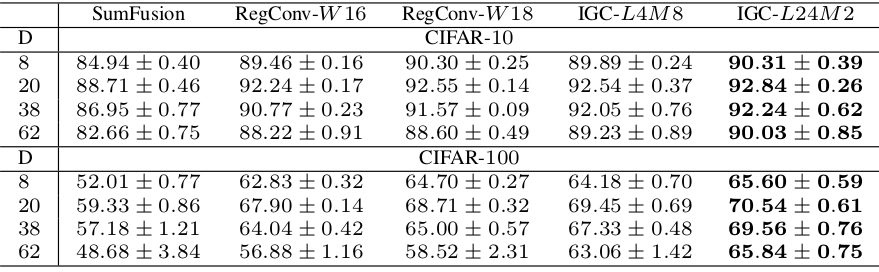
IGCV网络结构如下表所示,其中:RegConv-Wc 表示常规卷积, W 表示卷积核的尺寸为WxW,c 表示通道数量;Summation 表示加法融合层(即常规的1x1
卷积,而不是1x1 分组卷积)。
- 在
IGCV 块之后紧跟 BN 和 ReLU,即结构为:IGC block+BN+ReLU 。 4x(3x3,8) 表示分成4组,每组的卷积核尺寸为3x3 输出通道数为 8 。- 网络主要包含3个
stage,B 表示每个stage 的块的数量。 - 某些
stage 的输出通道数翻倍(对应于Output size 减半),此时该stage 的最后一个 block 的步长为2(即该block 中的3x3 卷积的步长为2) 。
IGCV网络的模型复杂度如下所示。
SumFusion 的参数和计算复杂度类似 RegConv-W16,因此没有给出。

3.IGCV模型在CIFAR-10 和 CIFAR-100 上的表现:

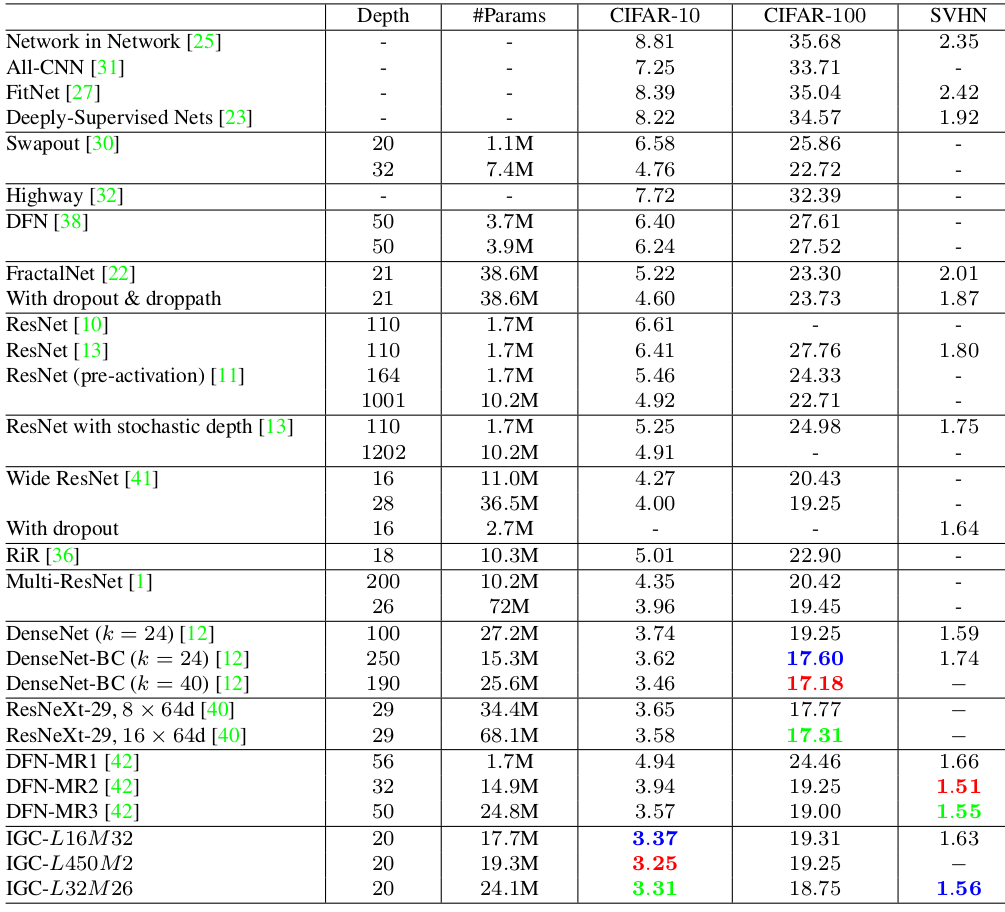
4.IGCV模型在ImageNet 上的表现:(输入224x224,验证集,single-crop )
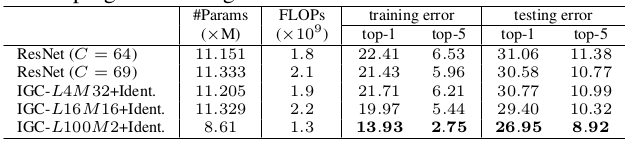
5.超参数L 和 M 的选取:
通过IGCV在CIFAR100 上的表现可以发现:L 占据统治地位,随着 L 的增加模型准确率先上升到最大值然后缓缓下降。
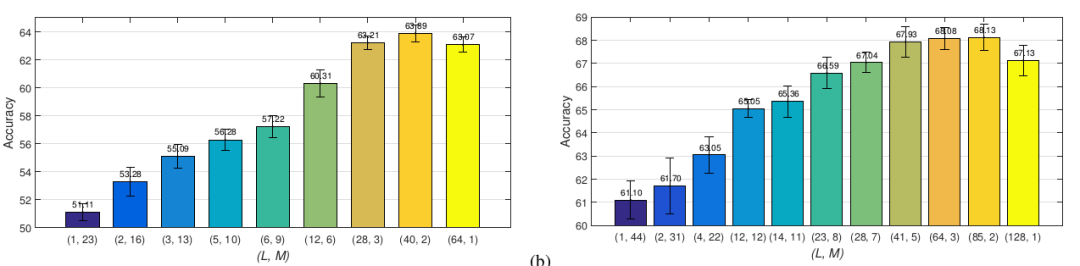
9.4.2 IGCV2
IGCV2 block 的主要设计思想是:将 IGCV block 两个结构化的稀疏卷积核组成的交错卷积推广到更多个结构化的稀疏卷积核组成的交错卷积,从而进一步消除冗余性。
9.4.2.1 IGCV2 block
假设输入feature map 的通道数为 ,卷积核尺寸为 ,输出通道数为 。考虑输入 feature map 的一个 patch(对应卷积核大小),该 patch 经过卷积之后的结果为: 。其中 是一个长度为 的向量, 是一个长度为 的向量, 是一个 行、 列的矩阵。
其中 至少有一个为块稀疏block-wise sparse 矩阵; 为置换矩阵,用于重新调整通道顺序; 为一个密集矩阵。
其中 表示第 i 层分组卷积的卷积核,它是一个block-wise sparse 的矩阵,其中第 j 组的卷积核矩阵为 。
- 对于
IGCV1 , 令 为第 i 层分组卷积的分组数,则: Xception、deep roots、IGCV1 的思想是:将卷积核 分解为多个稀疏卷积的乘积:
IGCV2 不是将
分解为 2个 block-wise sparse 矩阵的乘积(不考虑置换矩阵),而是进一步分解为 L 个块稀疏矩阵的乘积:
其中 为块稀疏矩阵,它对应于第 l 层分组卷积,即:IGCV2 包含了 L 层分组卷积; 为置换矩阵。
- 为了设计简单,第 l 层分组卷积中,每个分组的通道数都相等,设为 K_l 。
- 如下所示为一个
IGCV2 block 。实线表示权重 ,虚线表示置换 ,加粗的线表示产生某个输出通道(灰色的那个通道)的路径。
9.4.2.2 互补条件 & 平衡条件
事实上并不是所有的 L 个块稀疏矩阵的乘积一定就是密集矩阵,这其中要满足一定的条件,即互补条件complementary condition 。互补条件用于保证:每个输出通道,有且仅有一条路径,该路径将所有输入通道与该输出通道相连。
要满足互补条件,则有以下准则:
对于任意 m , 等价于一层分组卷积,且 也等价于一层分组卷积。且这两层分组卷积是互补的:第一层分组卷积中,同一个分组的不同通道会进入到第二层分组卷积的不同分组中;第二层分组卷积中,同一个分组的不同通道来自于第一层分组卷积的不同分组。
- 其物理意义为:从任意位置 m 截断,则前面一半等价于一层分组卷积,后面一半也等价于一层分组卷积。
- 可以证明
IGCV2 block 满足这种互补条件。
假设 IGCV2 block 的输入通道数为 C ,输出通道数也为 C ,其 L 层分组卷积中第 l 层分组卷积每组卷积的输入通道数为 。现在考虑 需要满足的约束条件。
对于IGCV2 block 的某个输入通道,考虑它能影响多少个IGCV2 block的输出通道。
设该输入通道影响了第 l 层分组卷积的 个输出通道。因为互补条件的限制,这 个通道在第 层进入不同的分组,因此分别归属于 组。而每个分组影响了 个输出通道,因此有递归公式:
考虑初始条件,在第1 层分组卷积有: 。则最终该输入通道能够影响IGCV2 block的输出通道的数量为: 。
由于互补条件的限制:每个输出通道,有且仅有一条路径,该路径将所有输入通道与该输出通道相连。因此每个输入通道必须能够影响所有的输出通道。因此有: 。
考虑仅仅使用尺寸为
1x1 和WxH 的卷积核。由于1x1 卷积核的参数数量更少,因此 L 层分组卷积中使用1层尺寸为 WxH 的卷积核、L-1 层尺寸为1x1 卷积核。
假设第1层为WxH 卷积核,后续层都是1x1 卷积核,则总的参数数量为: 。
当Block 的输出feature map 尺寸相对于输入feature map 尺寸减半(同时也意味着通道数翻倍)时,Block 的输出通道数不等于输入通道数。
设输入通道数为
,输出通道数为 ,则有:
平衡条件:设feature map 的尺寸缩减发生在3x3 卷积,则后续所有的1x1 卷积的输入通道数为 、输出通道数也为
。
选择使得 Q 最小的 L 有: 。因此对于feature map 尺寸发生缩减的IGCV2 Block,互补条件&平衡条件仍然成立,只需要将 C 替换为输出通道数。
9.4.2.3网络性能
IGCV2 网络结构如下表所示:其中 x 为网络第一层的输出通道数量,也就是后面 block 的输入通道数 C。
网络主要包含3个stage,B 表示每个stage 的块的数量。
某些stage 的输出通道数翻倍,此时该stage 的最后一个 block 的步长为2(即该block 中的3x3 卷积的步长为2) 。
每2个block 添加一个旁路连接,类似ResNet。即在 这种结构添加旁路连接。
表示输入通道数为 x 的 3x3 卷积。 表示输出通道数为 x 的 1x1 卷积。
L 和 K 为IGCV2 的超参数。 表示有 L-1 层分组卷积,每个组都是 K 个输入通道的1x1 卷积。事实上 IGCV2 每个
stage 都是 L 层,只是第一层的分组数为 1 。
- 对于
IGCV2(Cx),L=3 ;对于 IGCV2*(Cx), 。IGCV2* 的 (3x3,64) 应该修改为 。
2.通过一个简化版的、没有feature map 尺寸缩减(这意味着IGCV2 Block 的输入、输出通道数保持不变 )的IGCV2 网络来研究一些超参数的限制:
IGCV2 block 最接近互补条件限制条件 时,表现最好。如下所示,红色表示互补条件限制满足条件最好的情况。其中匹配程度通过 来衡量。
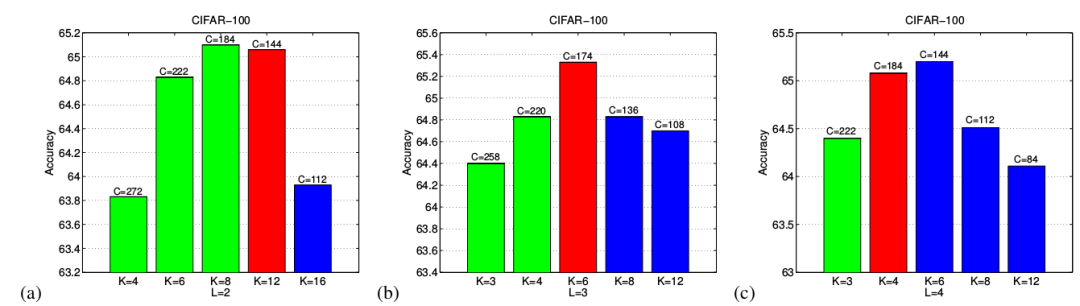
IGCV2 block的 L 最佳的情况是:网络的宽度(通过C 刻画)和稀疏性达到平衡,如下所示。
下图中,每一种 L 都选择了对应的Width (即 C )使得其满足互补条件限制,以及平衡条件,从而使得参数保持相同。
Non-sparsity 指的是IGCV2 block 等效的密集矩阵中非零元素的比例。
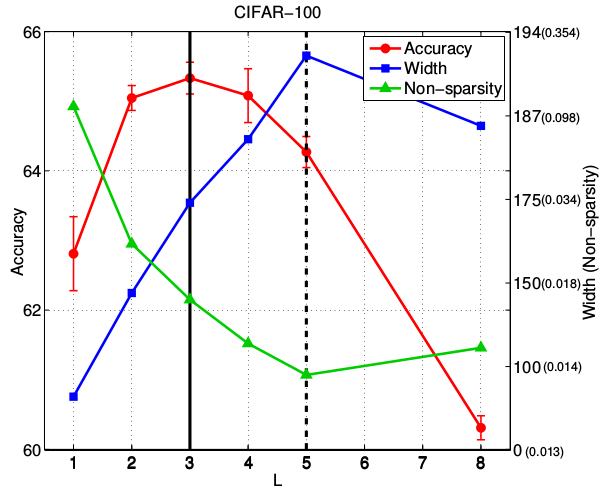
IGCV2 网络越深越好、越宽越好,但是加宽网络比加深网络性价比更高。如下图所示:采用 IGCV2* ,深度用 D 表示、宽度用 C 表示。
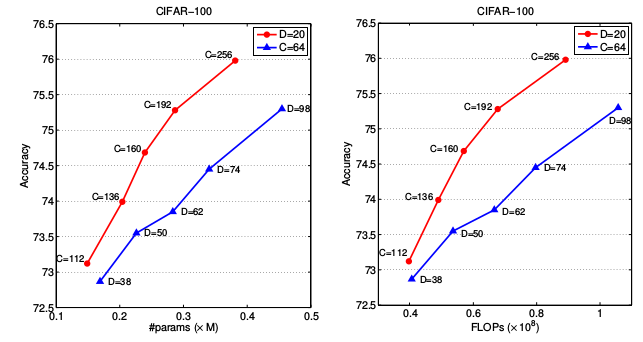
3.IGCV2 网络与不同网络比较:
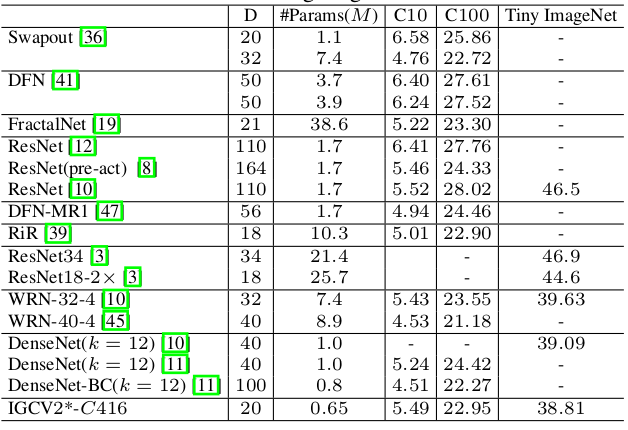
4.IGCV2 网络与MobileNet 的比较:(ImageNet)
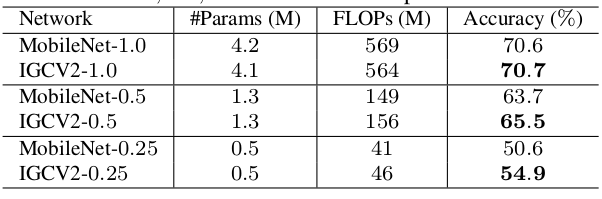
9.4.3 IGCV3
IGCV3 结合了块稀疏的卷积核(如:交错卷积) 和低秩的卷积核(如:bottleneck 模块),并放松了互补条件。
9.4.3.1 IGCV3 block
IGCV3 的block 修改自IGCV2 block ,它将IGCV2 block 的分组卷积替换为低秩的分组卷积。
按照IGCV2 的描述方式,输入 feature map 的一个 patch
,经过IGCV3 block 之后的结果为:
其中 为低秩的块稀疏矩阵; 为置换矩阵,用于重新调整通道顺序 。
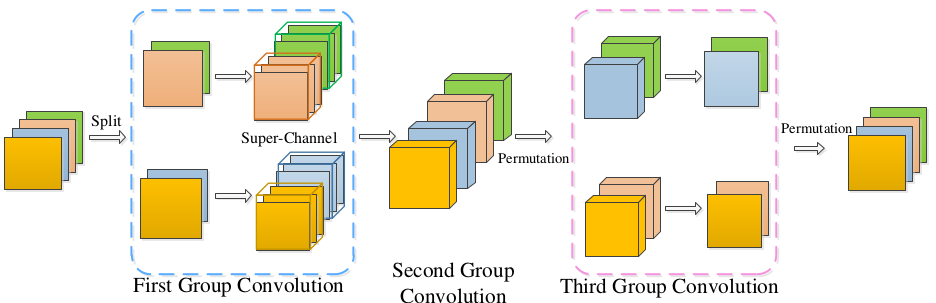
- 首先对输入
feature map 进行分组,然后在每个分组中执行 1x1 卷积来扩张通道数。 - 最后执行分组卷积,在每个分组中执行
1x1 卷积来恢复通道数,并对结果进行通道重排。
2.下图分别展示了IGCV1 block、Inverted 残差块、IGCV3 block 的区别。每个圆圈代表一个通道,箭头代表通道的数据流动。
IGCV1 块中,两层分组卷积的卷积核都是稀疏的;在Inverted 残差块中,两层1x1 卷积的卷积核都是低秩的;在IGCV3 块中,两层1x1 卷积的卷积核是稀疏的,也都是低秩的。
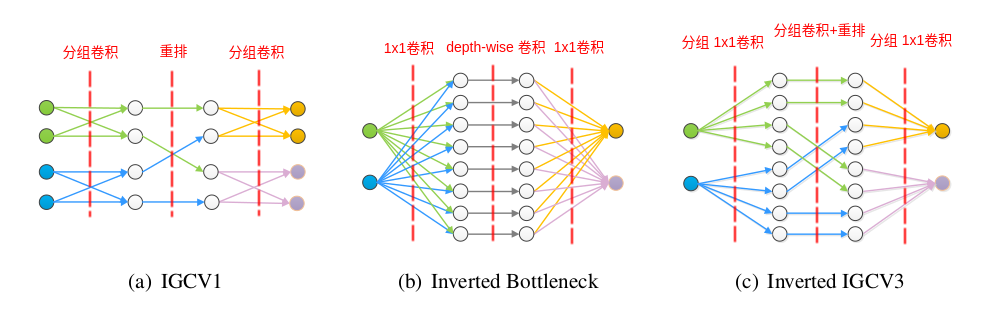
3.设IGCV3 block 第一层分组卷积(1x1 分组扩张卷积) 的分组数量为 ;第二层分组卷积(普通分组卷积)的分组数不变,也是 ;第三层分组卷积(1x1 分组压缩卷积)的分组数量为 。则 是非常重要的超参数。
9.4.3.2 loose 互补条件
实验中发现:如果IGCV3 block如果严格遵守互补条件会导致卷积核过于稀疏,从而导致更大的内存消耗而没有带来准确率的提升。
因此IGCV3 block提出了宽松互补条件loose complementary condition,从而允许输入通道到输出通道存在多条路径。
在IGCV3 block 中定义了超级通道 Super-Channel,设为 。在一个IGCV3 block 中,每个feature map 都具有同等数量的Super-Channel 。
- 输入
feature map 的通道数假设为 C ,因此每个输入超级通道包含 条普通的输入通道。 - 经过
1x1 分组卷积扩张的输出通道数假设为 ,则这里的每个超级通道包含 条普通的通道。 - 经过常规分组卷积的输出通道数也是 ,则这里的每个超级通道也包含
条普通的通道。
- 最后经过
1x1 分组卷积压缩的输出通道数也是 C,因此每个输出超级通道包含 条普通的输出通道。
loose complementary condition:第一层分组卷积中,同一个分组的不同超级通道会进入到第三层分组卷积的不同分组中;第三层分组卷积中,同一个分组的不同超级通道来自于第一层分组卷积的不同分组。
由于超级通道中可能包含多个普通通道,因此输入通道到输出通道存在多条路径。
通常设置 ,即:超级通道数量等于输入通道数量。则每条超级通道包含的普通通道数量依次为:{1,expand,expand,1},其中 expand 表示1x1 分组卷积的通道扩张比例。
也可以将 设置为一个超参数,其取值越小,则互补条件放松的越厉害(即:输入通道到输出通道存在路径的数量越多)。
9.4.3.3 网络性能
IGCV3 网络通过叠加IGCV3 block 而成。因为论文中的对照实验是在网络参数数量差不多相同的条件下进行。为了保证IGCV3 网络与IGCV1/2,MobileNet,ShuffleNet 等网络的参数数量相同,需要加深或者加宽IGCV3网络。
论文中作者展示了两个版本:
- 网络更宽的版本,深度与对比的网络相等的同时,加宽网络的宽度,记做
IGCV3-W。参数为: 。 - 网络更深的版本,宽度与对比的网络相等的同时,加深网络的深度,记做
IGCV3-D。参数为:。
IGCV3 与IGCV1/2 的对比:
IGCV3 降低了参数冗余度,因此在相同的参数的条件下,其网络可以更深或者更宽,因此拥有比IGCV1/2 更好的准确率。

3.IGCV3 和其它网络的在ImageNet 上的对比:
MAdds 用于刻画网络的计算量,单位是百万乘-加运算 。- 中的 表示宽度乘子,它大概以 的比例减少了参数数量,降低了计算量。
4.更深的IGCV 网络和更宽的IGCV 网络的比较:
- 更深的网络带来的效果更好,这与人们一直以来追求网络的
深度 的理念相一致。 - 在宽度方向有冗余性,因此进一步增加网络宽度并不会带来额外的收益。
5.ReLU的位置比较:
第一个IGCV3 block 的ReLU 位置在两个1x1 卷积之后;第二个IGCV3 block 的ReLU 位置在3x3 卷积之后;第三个IGCV3 block 的 ReLU 在整个block 之后(这等价于一个常规卷积+ReLU )。

6.超参数 的比较:
只要 都是输入、输出通道数的公约数时,loose 互补条件就能满足,因此存在 的很多选择。
实验发现, 比较小、 比较大时网络预测能力较好。但是这里的IGCV3 网络采用的是同样的网络深度、宽度。如果采用同样的网络参数数量,则 可以产生一个更深的、准确率更高的网络。

9.5 CondenseNet
CondenseNet 基于DenseNet网络,它在训练的过程中自动学习一个稀疏的网络从而减少了Densenet 的冗余性。
这种稀疏性类似于分组卷积,但是CondenseNet 从数据中自动学到分组,而不是由人工硬性规定分组。
CondenseNet 网络在GPU 上具有高效的训练速度,在移动设备上具有高效的推断速度。
MobileNet、ShuffleNet、NASNet 都采用了深度可分离卷积,这种卷积在大多数深度学习库中没有实现。而CondenseNet 采用分组卷积,这种卷积被大多数深度学习库很好的支持。
准确的说,CondenseNet 在测试阶段采用分组卷积,在训练阶段采用的是常规卷积。
9.5.1 网络剪枝
有一些工作(Compressing neural networks with the hashing trick、Deep networks with stochastic depth)表明:CNN网络中存在大量的冗余。
DenseNet 通过直接连接每个层的输出特征与之后的所有层来特征重用。但是如果该层的输出特征是冗余的或者不需要的,则这些连接会带来冗余。
CNN 网络可以通过权重剪枝从而在不牺牲模型准确率的条件下实现小型化。有不同粒度的剪枝技术:
- 独立的权重剪枝:一种细粒度的剪枝,它可以带来高度稀疏的网络。但是它需要存储大量的索引来记录哪些连接被剪掉,并且依赖特定的硬件/软件设施。
filter级别剪枝:一种粗粒度的剪枝,它得到更规则的网络,且易于实现。但是它带来的网络稀疏性较低。
CondenseNet 也可以认为是一种网络剪枝技术,它与以上的剪枝方法都不同:
CondenseNet 的网络剪枝发生、且仅仅发生在训练的早期。这比在网络整个训练过程中都采用L1 正则化来获取稀疏权重更高效。CondenseNet 的网络剪枝能产生比filter级别剪枝更高的网络稀疏性,而且网络结构也是规则的、易于实现的。
9.5.2 LGC
分组卷积在很多CNN 网络中大量使用。在DenseNet 中,可以使用3x3 分组卷积来代替常规的3x3 卷积从而减小模型大小,同时保持模型的准确率下降不大。
但是实验表明:在DenseNet 中,1x1 分组卷积代替1x1 常规卷积时,会带来模型准确率的剧烈下降。
对于一个具有 L 层的 DenseNet Block,1x1 卷积是第 层的第一个操作。该卷积的输入是由当前 DenseNet Block 内第 层输出feature map
组成。因此采用1x1 分组卷积带来准确率剧烈下降的原因可能有两个:
因此将这些输出feature 强制性的、固定的分配到不相交的分组里会影响特征重用。
- 第 层输出
feature 具有内在的顺序,难以决策哪些feature 应该位于同一组、哪些feature 应该位于不同组。 - 这些输出
feature 多样性较强,缺少任何一些feature 都会减小模型的表达能力。
一种解决方案是:在1x1 卷积之前,先对1x1 卷积操作的输入特征进行随机排列。
这个策略会缓解模型准确率的下降,但是并不推荐。因为可以采用模型更小的DenseNet 网络达到同样的准确率,而且二者计算代价相同。与之相比,特征混洗+1x1分组卷积 的方案并没有任何优势。
另一种解决方案是:通过训练来自动学习出feature 的分组。
考虑到第 层输出feature中,很难预测哪些feature 对于第 l 层有用,也很难预先对这些feature 执行合适的分组。因此通过训练数据来学习这种分组是合理的方案。这就是学习的分组卷积Learned Group Convolution:LGC 。
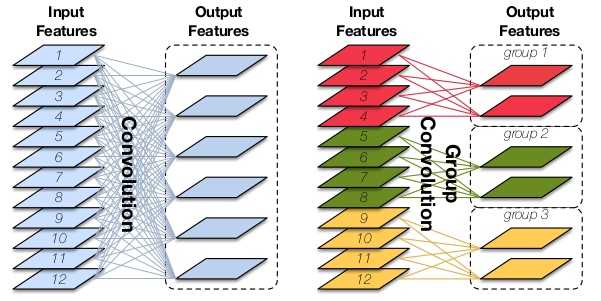
卷积操作被分为多组filter,每个组都会自主选择最相关的一批feature 作为输入。由于这组filter 都采用同样的一批feature 作为输入,因此就构成了分组卷积。
允许某个feature 被多个分组共享(如下图中的Input Feature 5、12),也允许某个feature 被所有的分组忽略(如下图中的Input Feature 2、4)。
即使某个feature 被第 l 层1x1 卷积操作的所有分组忽略,它也可能被第 l+1 层1x1 卷积操作的分组用到。
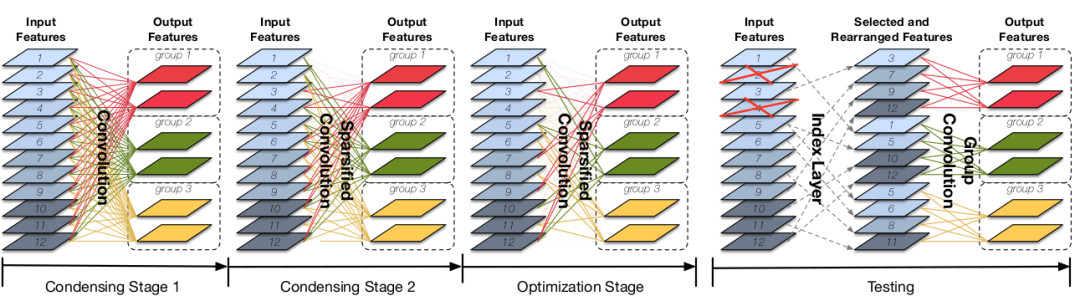
9.5.3 训练和测试
CondenseNet 的训练、测试与常规网络不同。
CondenseNet 的训练是一个多阶段的过程,分为浓缩阶段和优化阶段。
浓缩阶段condensing stage:训练的前半部分为浓缩阶段,可以有多个condensing stage (如下图所示有2个浓缩阶段)。每个condensing stage
重复训练网络一个固定的iteration,并在训练过程中:引入可以产生稀疏性的正则化、裁剪掉权重幅度较小的filter 。
优化阶段optimization stage:训练的后半部分为优化阶段,只有一个optimization stage。
在这个阶段,网络的1x1 卷积的分组已经固定,此阶段在给定分组的条件下继续学习1x1 分组卷积。
CondenseNet 的测试需要重新排列裁剪后的filter,使其重新组织成分组卷积的形式。因为分组卷积可以更高效的实现,并且节省大量计算。
通常所有的浓缩阶段和所有的优化阶段采取1:1 的训练epoch 分配。假设需要训练 M 个epoch,有N 个浓缩阶段,则:
所有的浓缩阶段消耗 个epoch,每个浓缩阶段消耗 个epoch 。
假设卷积核的尺寸为 ,输入通道数为 ,输出通道数为 。当采用1x1 卷积核时4D 的核张量退化为一个矩阵,假设该矩阵表示为
。
将该矩阵按行(即输出通道数)划分为同样大小的 G 个组,对应的权重为: 。其中 对应第 g 个分组的第i 个输出特征(对应于整体的第 个输出特征)和整体的第 j 个输入特征的权重。
CondenseNet 在训练阶段对每个分组筛选出对其不太重要的特征子集。对于第 g 个分组,第 j 个输入特征的重要性由该特征在 g分组所有输出上的权重的绝对值均值来刻画: 。如果 相对较小,则删除输入特征 j ,这就产生了稀疏性。
考虑到LGC 中,某个feature 可以被多个分组分享,也可以不被任何分组使用,因此一个feature 被某个分组选取的概率不再是 。定义浓缩因子 C,它表示每个分组包含 的输入。
如果不经过裁剪,则每个分组包含 C_I 个输入;经过裁剪之后,最终保留 比例的输入。
filter 裁剪融合于训练过程中。给定浓缩因子 C,则CondenseNet 包含 C-1 个condensing stage (如上图中,C=3 )。在每个condensing stage 结束时,每个分组裁剪掉整体输入 比例的输入。经过 C-1 个condensing stage之后,网络的每个分组仅仅保留 的输入。
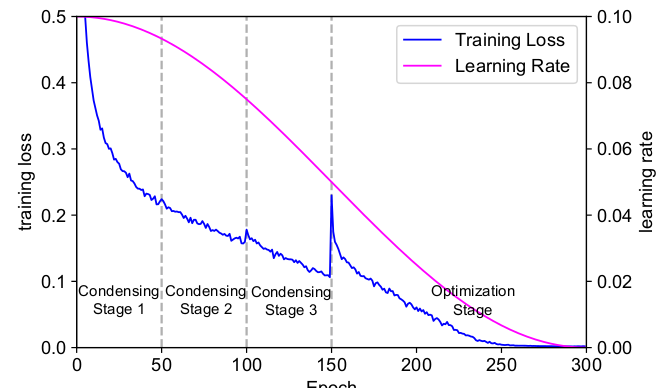
在每个condensing stage 结束前后,training loss 都会突然上升然后下降。这是因为权重裁剪带来的突变。
最后一个浓缩阶段突变的最厉害,因为此时每个分组会损失 50% 的权重。但是随后的优化阶段会逐渐降低training loss 。
下图中,学习率采用cosine 学习率。
5.训练完成之后,CondenseNet引入index layer 来重新排列权重裁剪之后剩下的连接,使其成为一个1x1分组卷积。
下图中:左图为标准的 DenseNet Block,中间为训练期间的CondenseNet Block,右图为测试期间的CondenseNet Block 。
- 测试时,
1x1 卷积是一个index layer
加一个1x1分组卷积。
6.在训练早期就裁剪了一些权重,而裁剪的原则是根据权重的大小。因此存在一个问题:裁剪的权重是否仅仅因为它们是用较小的值初始化?
论文通过实验证明网络的权重裁剪与权重初始化无关。
9.5.4 IGR 和 FDC
CondenseNet 对 DenseNet 做了两个修改:
递增的学习率increasing growth rate:IGR :原始的DenseNet 对所有的DenseNet Block 使用相同的增长率。考虑到DenseNet 更深的层更多的依赖high-level 特征而不是low-level 特征,因此可以考虑使用递增的增长率,如指数增长的增长率: ,其中 m 为 Block 编号。该策略会增加模型的参数,降低网络参数的效率,但是会大大提高计算效率。
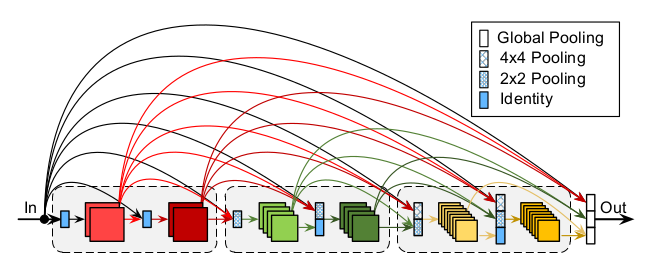
全面的连接fully dense connectivity:FDC
:原始的DenseNet 中只有DenseNet Block 内部的层之间才存在连接。在CondenseNet 中,将每层的输出连接到后续所有层的输入,无论是否在同一个CondenseNet Block 中。如果有不同的feature map 尺寸,则使用池化操作来降低分辨率。
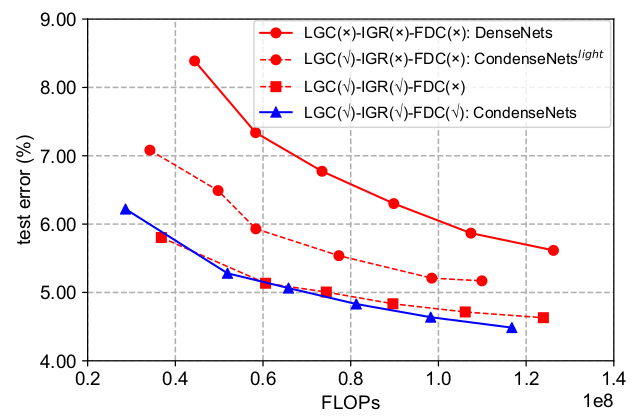
对LGC、LGR、FDC 的实验分析如下:(CIFAR-10 数据集)
配置:默认 k=12,3x3 卷积为分组数量为4的分组卷积。
LGC:learned group convolution:C=4 ,1x1 卷积为LGC 。
IGR:exponentially increasing learning rate: 。
FDC:fully dense conectivity 。
第二条线和第一条线之间的gap 表示IGC 的增益。
第三条线和第二条线之间的gap 表示IGR 的增益。
第四条线和第三条线之间的gap 表示FDC 的增益。FDC 看起来增益不大,但是如果模型更大,根据现有曲线的趋势FDC 会起到效果。
9.5.5 网络性能
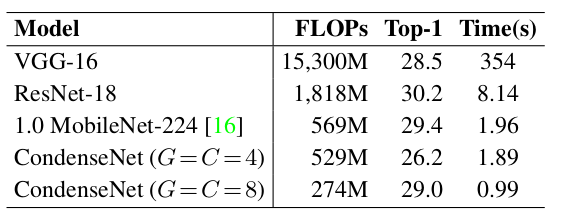
CondenseNet 与其它网络的比较:(* 表示使用cosine 学习率训练 600个 epoch)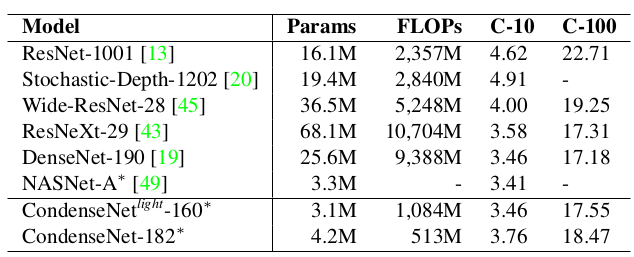
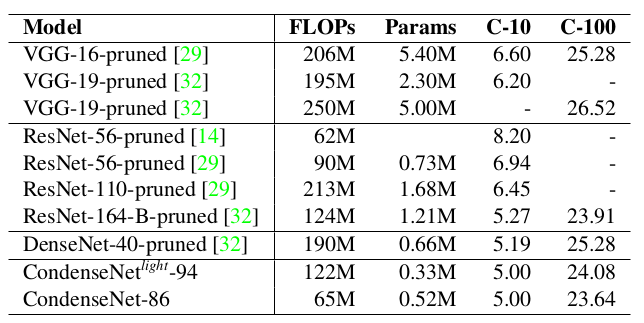
2.CondenseNet 与其它裁剪技术的比较:
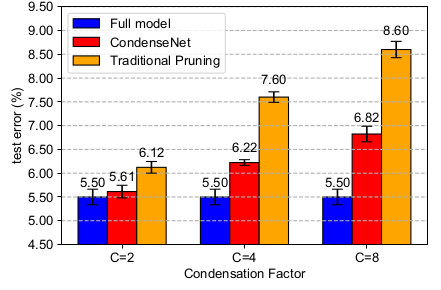
3.CondenseNet 的超参数的实验:(CIFAR-10,DenseNet-50 为基准)
Traditional Pruning :在训练阶段(300个epoch)完成时执行裁剪(因此只裁剪一次),裁剪方法与LGC 一样。然后使用额外的300个 epoch 进行微调。
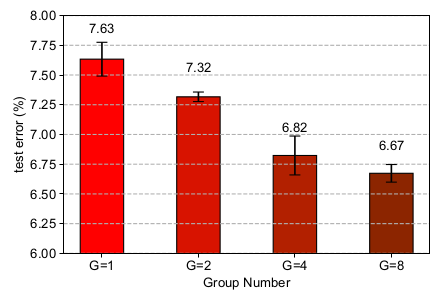
随着分组数量的增加,测试误差逐渐降低。这表明LGC 可以降低网络的冗余性。
浓缩因子:(G=4) 可以看到: 可以带来更好的效益;但是 C>1 时,网络的准确率和网络的FLOPs 呈现同一个函数关系。这表明裁剪网络权重会带来更小的模型,但是也会导致一定的准确率损失。
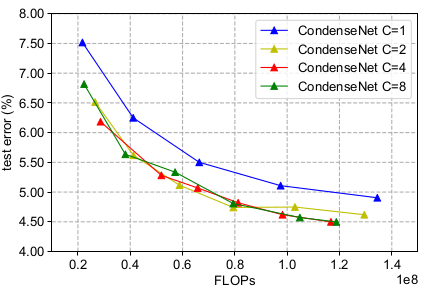
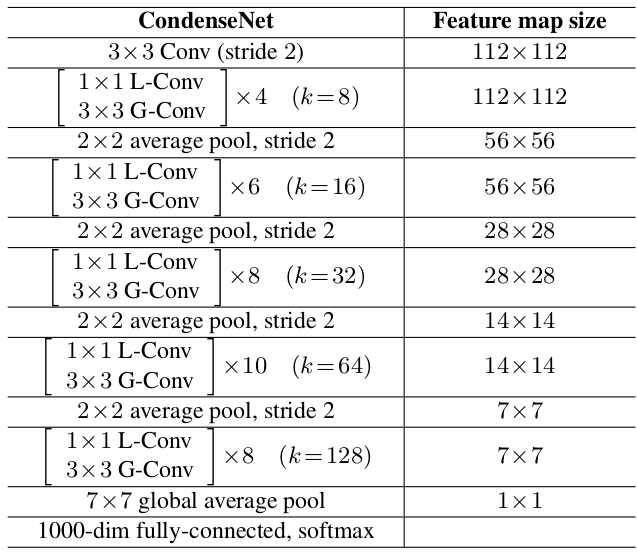
4.在ImageNet 上的比较:
网络结构:为了降低参数,在epoch 60 时(一共120个epoch )裁剪了全连接层FC layer 50% 的权重。思想与1x1 卷积的LGC 相同,只是 G=1,C=2 。
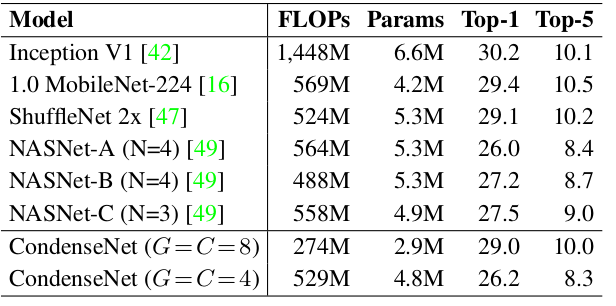
网络在ARM 处理器上的推断时间(输入尺寸为224x224 ):