译者：张雨佳
人们很难真正通过数学理解东西，你只需要去习惯并使用它。
——约翰·冯·诺伊曼
在机器学习中，我们已经习惯了使用梯度下降法解决问题，以至于没人去质疑它为什么有效。
大家经常将梯度下降法模拟为爬山：要想找到崎岖地形中的顶峰（或低谷），就必须先观察陡坡上升（或下降）的方向，并向那里迈出一步。这个方向就被定义为梯度，沿着梯度找到局部极值的迭代过程称为梯度上升或梯度下降。上升用来寻找顶峰，下降用来寻找低谷。
但这并不是精确的数学解释。有许多问题都没有得到解答，我们也不清楚算法到底为什么有效。
如果不准确理解梯度下降法的真正原理，我们只能盲目地去使用它。而这篇文章的目的就是介绍一个合适的数学框架，帮助你理解其背后的具体操作。在你真正理解梯度下降法后，就可以有目的地提高它在项目中的性能。
本文将从以下几方面具体介绍：
1）用微分表示变化率
2）一阶和二阶导数的优化原理
3）微分方程的基础知识
4）梯度下降等价于向平衡状态流动的物理系统
导数及其含义
首先需要了解的是导数，根据定义，如果函数 在 处可导，就要保证下式存在。
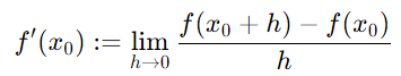
称
为导数。尽管这个定义看似随意，但它背后具有深刻的含义：可以将变化率看作为导数。
将导数作为速度
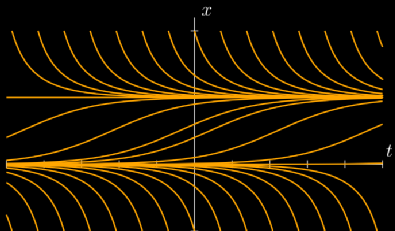
让我们将目光转回到几百年前。最初，导数的出现是为了描述物体的移动速度。简单起见，假设物体沿着直线运动，t时刻的物体位置由函数 给出，如下图所示。
我们的目标是计算物体在特定时间的速度。在高中时，我们学到：
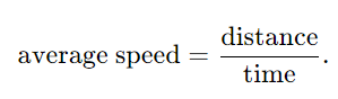
将其转换为定量形式，如果 是两个任意时间点，且 ，则平均速度为：
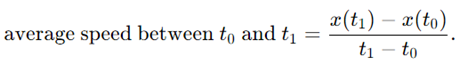
我们将上述公式叫做微分系数。当物体向后移动时，平均速度就为负。
平均速度可以通过简单的几何方式解释。如果你将物体的运动近似成以平均速度行动的匀速运动，那么物体在相同时间会处于同一位置。在图中表示， 和 间连线的斜率就等价于平均速度。
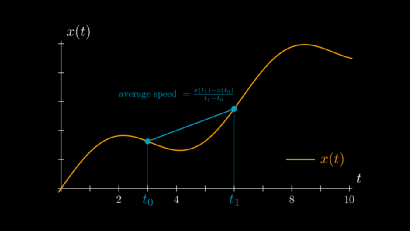
基于上述原理，我们可以进一步计算出在单个时间点 的准确速度。其思想很简单：随着时间间隔 的减小，那在 到 之间的平均速度就应该越来越趋近于 时刻的速度(Δt也可以为负)。
因此，
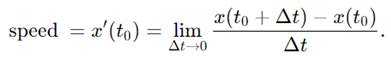
从几何上看，导数就是 点的切线，而微分系数则是图中连接 和 之间直线的斜率。
局部极值及其导数
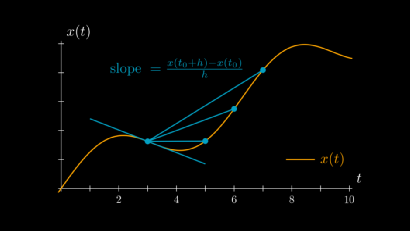
导数比速度具有更多的含义。根据上文介绍，我们知道导数等于切线的斜率。那我们再看一下下面这张图。
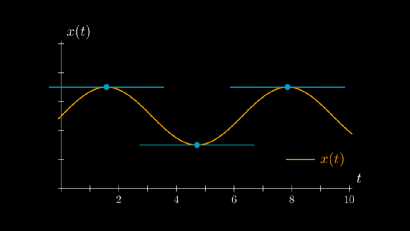
可以看到，切线在局部极小值和极大值时都是完全水平的。用数学术语来说，此时 ，那我们能利用这个性质找到函数的极小值和极大值吗？
答案是肯定的，但没那么简单。例如对于函数 ，当t为0时的导数也为零，但此处既不是局部极小值，也不是局部极大值。此时我们能做的就是继续计算其二阶导数，希望它能给出一些清晰的信息。经过验证，有以下定理。
定理：设 是一个在任意 处都二阶可导的任意函数。
（a）如果 且 ，那么a就处于局部极小值。
（b）如果 且 ，那么a就处于局部极大值。
为什么我们要关注这些导数问题？因为大部分机器学习是一个大型的优化问题。构造一个包含大量参数的模型，然后找到一组可以使其性能最大化的参数。这个寻优过程就是通过著名的梯度下降算法完成的，它看起来和我们计算的二阶导数结果没有任何关系。但事实恰恰相反：梯度下降法的核心包括了局部极值、一阶和二阶导数的关系。
下面，我们将介绍其中的原因。
什么是微分方程
方程在数学中起着至关重要的作用，其背后具有深刻的原理。通常，方程是对系统的建模，比如生物化学网络中的相互作用、经济变化过程和许多其他系统。例如，对生物体内的代谢过程进行建模就会得到下面的线性方程：
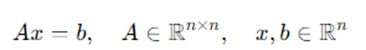
其中向量x和b代表分子的浓度（其中x是未知数），矩阵A代表它们之间的相互作用。我们学过一些线性方程的知识，所以很容易对方程进行求解。
但由于这些方程缺少时间变量，因此不适合模拟动态系统。比如我们想要建立描述空间站绕地球运行轨迹的模型，就必须使用函数及其导数方法。
例如，摆动钟摆的轨迹可以用下面的等式描述：
其中，
是描述钟摆与垂直方向的角度，L是挂有质量为m物体的（无质量）杆长度，g是重力加速度常数，约为9.7m/s2。
根据导数的原始定义，如果 描述了钟摆在时间t时的运动，那么 和 就是对时间t的微分，用于描述物体的速度和加速度。实际上，微分方程 的解是牛顿第二运动定律。
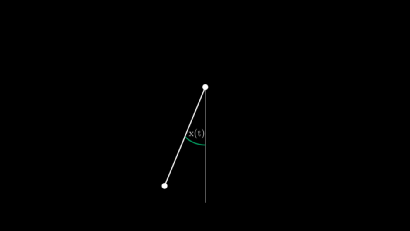
涉及函数及其对应导数的方程称为常微分方程（ordinary differential equations），或简称为ODEs，如上面的钟摆摆动方程。毫不夸张地说，自17世纪以来，对常微分方程的研究大大推动了数学领域的发展。我认为微分方程是数学中最美的东西之一，并且梯度下降算法实际上就是微分方程的近似解。
这篇文章的第一部分是对微分方程的快速入门，将主要围绕Steven Strogatz写的书《Nonlinear Dynamics and Chaos（非线性动力学和混沌）》展开介绍。
常微分方程的一般形式
让我们直接通过示例，从微分方程中最难的地方开始学习。最简单的微分方程是下面的等式：
其中，微分是对时间变量t进行的。如果 是细菌菌落的数量，则上述方程描述了无限增长的菌落数量的动态变化。 代表菌落增长的速度：如果没有空间和营养的限制，每一个细菌细胞都可以在任何时候自由复制与分裂，并依据菌落的数量进行生长。
简单来说，上述方程的解为导数是自身的函数。通过计算，我们可以得到一组解： ，其中 是任意常数（因为我们学过，初等函数et的导数就是它本身）。
如下图所示是方程的一组解。
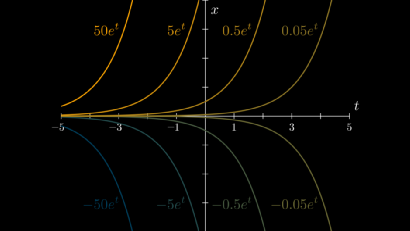
我们要记住两个知识点：一是微分方程描述了随时间变化的动态过程，二是方程可以有多个解。每个解由两个因素决定：一是方程本身，二是初始条件 。如果我们设定了初始条件，则c的值可以由下式计算得出：
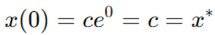
因此，常微分方程有一组解，每个解都由初始条件决定。所以，我们应该用更一般的术语来讨论微分方程。
定理：（一阶常微分方程）设 为可导函数，则称方程式：
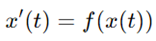为一阶齐次常微分方程。
当定义较清晰时，可以省略对t的依赖关系，将上式简写为 。
术语“一阶齐次常微分方程（first-order homogeneous ordinary differential equation）”包含了过多复杂、难理解的定语。下面将其拆解开，逐个进行分析。
微分方程是一个包含导数的函数方程。由于唯一的变量就是时间t，因此微分方程是“ordinary”的，与涉及多变量函数和偏导数的微分方程相反。由于只存在一阶导数，因此称为“first-order”。以此类推，“second-order”就会包括二阶导数。最后，由于等式右边的 并不明确依赖于时间变量t，所以该方程在时间上是“homogeneous”的。“homogeneous（齐次）”意味着动态系统的规则不会随时间而发生改变。
不要被 的复杂形式所吓到。例如在等式 中，f的作用是投影到恒等函数 上。一般来说，
是对 （可以是位置、密度等函数）及其导数，也就是变化率之间建立对应关系。
正如上述介绍的，我们可以根据微分方程和初始条件来得出函数的解。下面将其转换为恰当的数学定义。
定理：（初值问题）设 是一阶齐次常微分方程，且 为任意数，则称系统：
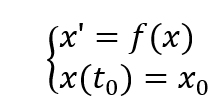
为初值问题。
如果函数 满足上述两个条件，就说它是初值问题的解。
通常，我们有选择时间原点t0的自由，一般令t0为0。
但是事情并不像看起来这么简单，微分方程和初值问题通常很难解决。除了一些简单情况，我们很难找到方程的精确解。在这种情况下，我们有两种解决方式：一是通过数值方法构造近似解，二是求助于定性方法去研究解的行为，而不直接进行求解。
我们首先讨论定性方法，将从几何的角度来深入了解微分方程是如何工作的。
微分方程的几何解释
当我们寻找不到方程的可行解时，可以转而去关注其短期和长期行为，寻找解的定性理解，而不单单盯着公式。
当给定一个微分方程如下：
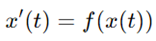
并且你对特定时刻如t0时初值为 的解感兴趣。例如，你可能正在研究细菌群落的动态变化情况，并希望构建一个预测模型来拟合最新的观测值 。那么你如何快速找到模型的解呢？
可以看出，如果 且 ，那么常数函数 就是模型的一个解！这种解叫做平衡解（equilibrium solution），它正式的数学定义如下。
定理：（平衡解）令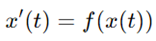为一阶齐次常微分方程，且 为任意数。如果有 ，那么 被称为方程 的平衡点。
对于平衡点，常数函数 是方程 的解，并且是平衡解。
回到最初的例子，对于最简单的常微分方程 。我们可以将这个方程理解为理想条件下无限制的种群增长模型。只有当 且在x=0时，函数值为零，所以常数函数 是方程的解。这可以解释为：如果一个种群初始时有0个个体，那么它的规模不会发生变化。换句话说，系统处于平衡状态。
就像一个停止摆动并在最底部处于静止的钟摆。不过钟摆有两个平衡点：一个在顶部，一个在底部，我们假设物体由一根无质量的杆支撑。你可以推动底部悬挂的物体，经过一段时间后它会回到静止状态。但在顶部，任何微小的推动都会破坏平衡状态，并且再也不会回到该状态。
为了解释这一现象，我们可以看下面这个例子：著名的逻辑（logistic）方程
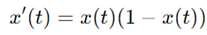
从种群动态变化的角度来看，如果方程
描述了细菌菌落的无限制生长，逻辑方程则模拟了在资源有限制下的种群生长。我们假设1是种群的总容量，那当种群数量接近这个极限值时，就会限制种群的增长速度。因此，可以将种群的变化率 建模为
，其中 项会随着种群数量接近总容量而减慢增长。
我们可以通过 的映射关系，写出逻辑方程的一般形式 。你还记得导数和单调性的关系吗？微分方程 揭示了解的变化过程，具体来说：
我们可以在相位图中将其可视化：
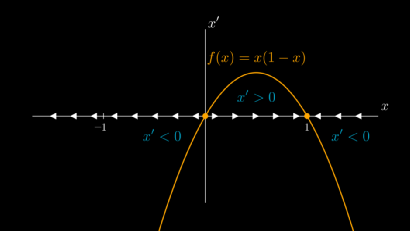
可以看出，单调性会描述方程的长期行为：
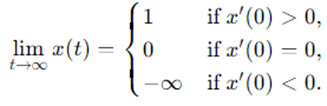
通过很少的计算量，我们可以得出方程的解为：
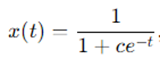
其中 是任意常数。当c=1时，方程就是常用的Sigmoid函数。你可以手动验证这个解的合理性，还可以将其绘制到图中，如下所示：
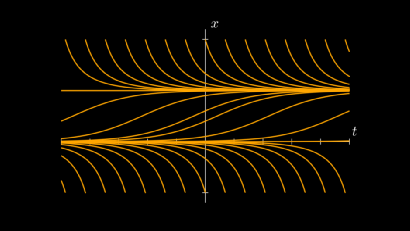
可以看出，解的单调性和我们预测的一样。
我们可以根据解的长期行为来预测平衡点（在逻辑方程中，平衡点是0和1）的特征。这可以与函数f的短期行为进行联系：如果f的值在平衡点 附近减小，那它会趋近于附近可行的解。但如果f的值在 附近增加，则会远离附近的解。
这就产生了稳定和不稳定平衡的概念。
定理：（稳定和不稳定平衡）令 是一阶齐次常微分方程，并且f是可微的， 是方程的一个平衡点。
如果对于所有 都在平衡点 的邻域 附近，那初值问题的解
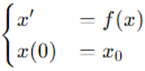
会向 汇聚，即 。如果 处不稳定，就叫不稳定平衡。
在逻辑常微分方程 中， 是稳定平衡， 则是不稳定平衡。从种群数量的动态变化方面进行解释：平衡点 表示数量达到最大容量，如果种群数量大于容量1，则一些样本会因饥饿而死亡。而当种群数量略小于1时，数量就会继续增长以达到容量限制。另一方面，无论种群数量有多小，在理想情况下都不会灭绝。
连续情况下的梯度上升
现在讲回函数 的最大化问题。假设F是二阶可导的，用 来表示其导数。那么，我们可以通过计算F的二阶导数来得到局部极大值，寻找符合 且
的 。
这是不是很眼熟，如果 也成立，那么 就是方程的平衡解。并且由于 ，它会趋近附近可行的解。这意味着如果 是符合上述条件的，那 就是以下初值问题的解。
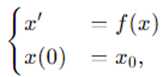
即 。换句话说，解会向 处收敛，也就是函数F的局部极大值处！这就是连续情况下的梯度上升方法。
这看起来很容易实现，但实际上还存在很多问题。因为大部分的微分方程都很难求解，我们很难找到求解函数F的方向。幸运的是，我们可以用近似方法去逼近解。
作为离散微分方程的梯度上升
实际计算导数时，通常将前向之差在数值上近似为导数：
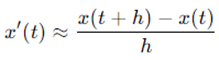
如果 确实是对应初值问题的解，那就太幸运了！但大部分情况下，我们将前向差分代入微分方程中，从0向前迈出一小步，进而逼近 。用数学表达式实现：
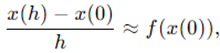
从而得到：
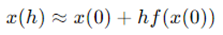
并定义 和 为：
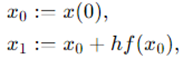
并且 会约等于
。这看起来是梯度上升的第一步，之后再次使用前向差分，这次从点 开始逼近，得到如下公式：
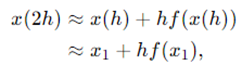
通过定义，我们知道 ，那么联立上式可以得到 约等于 。不过在 中会积累两种近似误差：首先是前向差，然后是前一步的近似误差。
这种方式会引导我们去定义递归序列：
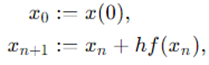
正如公式中所暗示的，我们同样可以用 去近似 。这个递归序列本身就是梯度上升算法，小步长h相当于学习率！这同样也是微分方程中的欧拉（Euler）算法。
如果我们不深究具体细节，当h足够小，并且预测到的函数f的行为是正确的，那么就可以使用欧拉算法收敛到平衡解 。
现在就剩最后一步了：将梯度上升转换为梯度下降。实际操作非常简单，梯度下降就是对-f函数应用梯度上升。因为最小化函数f与最大化-f的结果是一样的。最终，我们实现了著名的梯度下降算法，它是动态系统向稳定平衡处收敛的结果。
梯度上升的运作方式
为了明确梯度上升（即欧拉算法）的具体作用，我们回到最初的逻辑方程 中。假设我们想找到下面函数的局部极大值：
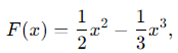
其曲线如下图所示：
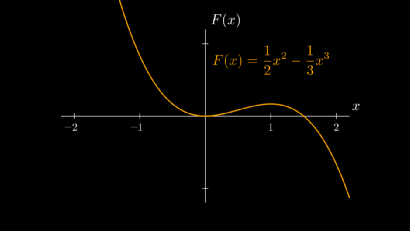
首先，我们可以利用所学知识，通过计算其导数 ，得出在 时是局部极大值。当然，你最好自己拿笔验证一遍。
由于 且 ，因此点 是下式逻辑方程的稳定平衡点。
因此，如果初值 足够接近 ，那初值问题的解 为：
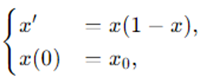
且 。实际上，无论我们选择无穷区间 中任意时刻的初始值 ，最终都会收敛到该处。将欧拉方法离散化表示，就能得到如下的递归序列：
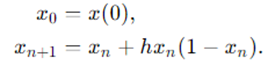
我们将通过欧拉算法求解 的可视化结果展示如下。为了便于观察，初始值设为t0=-5。
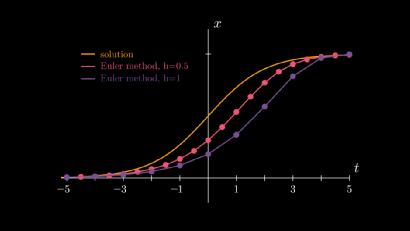
我们还可以把欧拉算法得到的离散解，画在 图上。
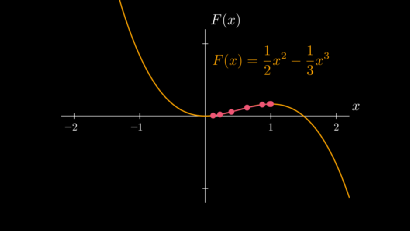
结论
所有上文介绍到的知识，都是为了去理解梯度下降算法的原理。
梯度下降算法是机器学习中最重要的优化算法，其核心原理很简单：想要找到函数的局部极小值，就要先找到它下降的方向，然后向那里迈出一小步，这个看似朴素的想法其实蕴含了很多微分方程的基础知识。
如果我们把函数看作决定动态系统的规则，那么局部极值就对应于平衡状态。那么当用微分方程描述动态系统时，求取局部极值的过程就是逼近其平衡状态。从这个观点来看，梯度下降算法只不过是求取方程数值解的一个方法。
到目前为止，我们只研究了单变量情况下的函数，而机器学习是在数百万个维度上进行的。尽管如此，我们可以将其作为研究多变量和高维空间函数的指南。虽然研究的对象更复杂了，但他们背后的原理一样。
多变量微积分中的最大困难是处理的复杂性，不过向量和矩阵操作可以帮我们负担大部分的繁重计算。不过这是下一步要研究的东西了。
- 机器学习交流qq群955171419，加入微信群请扫码
